基于PCNN和FCM的钢带表面缺陷检测
亢伉
(宝鸡文理学院 陕西 宝鸡 721016)
基于PCNN和FCM的钢带表面缺陷检测
亢伉
(宝鸡文理学院 陕西 宝鸡 721016)
针对目前还没有较好的方法正确的检测金属钢带表面缺陷,提出一种结合耦合神经网络(PCNN)和模糊C-均值(FCM)的钢带表面缺陷检测算法,首先通过有效性指数求得聚类中心,其次用PCNN最短路径法确定目标函数极小值,最后通过改进的FCM分割目标。通过对比实验表明,该算法能够快速的分割出缺陷目标,正确率在95﹪以上。
缺陷检测;最短路径;耦合神经网络;模糊聚类
金属钢带广泛的应用于机械制造、汽车、造船、航空航天等领域,是其重要的原材料。由于金属钢带的生产环节及环境相当复杂,会产生夹杂、氧化铁皮压入、斑迹、辊印、擦伤等表面缺陷,如不及时发现处理,会对最终产品的外观、性能造成不良影响,甚至造成产品降级或者报废,因此,钢带表面的缺陷检测具有重要的意义和经济价值。
传统的钢带表面缺陷检测依靠大型自动化设备完成,这种设备不但价格昂贵而且误检率高,对于安装环境有较高要求。近年来,随着计算机的飞速发展,机器视觉的方法得到了广泛的应用,国内外的学者提出了一些基于图像的钢带表面监测算法。电子科技大学的罗新斌等人[1]提出一种基于统计学习背景模型的检测算法,这种方法需要人工设置阈值,自适应能力差;武汉科技大学的梁文豪[2]提出一种BP的神经网络算法,这种算法需要提前进行大量模型训练;华中科技大学的谭绍华[3]提出一种基于Sobel和PHOT的检测算法,这种算法对于噪声的抑制较差;Kumar[4]提出一种小波分解钢带图像的算法;Borselii[5]提出一种神经网络的算法,但是上述算法都停留在理论研究阶段。
根据钢带表面的缺陷特征,提出一种快速的缺陷检测算法。通过有效性指数求得聚类中心,再用PCNN最短路径法确定目标函数极小值矩阵,最后代入改进的FCM算法分割目标。实验结果表面,本文提出的算法检测缺陷精确,运算速度快。
1 改进的PCNN最短路径算法
1.1 经典PCNN模型
上世纪九十年代,Eckhorn,Johnson等人提出了一种第三代人工智能神经网络-耦合脉冲神经网络 (Pulse Coupled Neural Network,PCNN)。PCNN通过神经元相互之间的脉冲触发耦合,使其具有不需要提前进行模型训练的优点[6]。
PCNN神经元的基本结构如图1所示,由3个部分组成:接收域、调制域和脉冲产生域。接收域有两条通道,分别是接受来自上一级神经元脉冲Lij的L通道和接受外部固定输入Ij的F通道,L通道和F通道的信号变化分别如公式(1)、(2)所示。其中,当接收到上一级脉冲信号时,L通道为1,否则为0。

在调制部分,调制结果Uij由连接输入Lij和反馈输入Fij两部分调制得到,如公式(3)所示,其中,β为连接系数。

在脉冲产生部分,通过比较调制结果Uij与神经元的动态门限θij来判断是否发射脉冲信号。θij由公式(3)决定,神经元的输出Yij是一个阶跃函数,当调制结果Uij大于动态门限θij时点火,输出1,否则输出0。整个过程称之为神经元的一次脉冲,如公式(4)所示。

图1 PCNN神经元模型Fig.1 Model of PCNN nerve cell

利用PCNN寻求最短路径的原理可以大致描述为:路径图中每一个节点分别对应该一个神经元,各神经元是一种级联关系,即神经元与它的前一级神经元相连。首先点火起始神经元,同时其他神经元均不点火;然后所有可能路径上的神经元被纷纷点火,且每个神经元只点火一次;最后,直到终点神经元点火后停止寻找,此时就得到了最短路径。
1.2 改进的PCNN最短路径算法
由于经典PCNN算法参数较多,计算复杂,迭代点火速度较慢,不利于钢带表面的快速检测。提出一个快速寻找最短路径的PCNN算法。
连接系数β反映的是此神经元的特征与其邻域像素的相关性,相关性越大,越容易点火。因此,连接系数β应该与神经元的相关程度有关,提出一种自适应的确定连接系数β的方法。
神经元之间的点火时延可以称之为神经元之间的距离d,两者距离越近,则点火越早,相关性越大。因此,神经元之间的距离d与其连接系数β相关,这些相关的神经元就比其他输入神经元更容易被捕获点火,反之亦然。连接系数β的确定公式为

其中,下标i,j表示数字图像中的某个像素,f为图像的灰度值。
所有神经元按照公式(5)进行点火,某一条路径上门限θij由上级神经元和上级输出共同决定,当该路径上门限增大到一个非常大的值时,该路径不会被再次点火。因为每一条路径两两神经元距离d不同,所以每一条路径的点火时间肯定不会完全相同,根据图伦的最短路径理论,最先始终点神经元点火的路径就是最短路径。
2 改进的FCM图像分割
2.1 经典FCM算法
模糊C均值聚类(FCM)是最经典、应用最广泛的模糊聚类图像分割算法。通过对最小化目标函数过程实现数据集的模糊划分,判断准则是最小类内平方误差[7]。
首先提取图像所有像素特征值并构成数据集Data={X1,X2,…,XN},并且依据目标函数最小化原则将图像像素分为K类,目标最小化函数J(U,C)表达式为
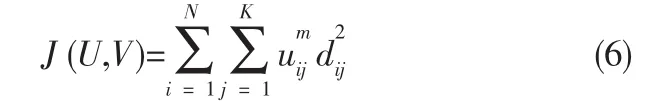
其中,V={v0,v1,…,vK-1}为聚类中心矢量的集合,m为隶属度函数指数m∈[2,∞],为模糊聚类矩阵,用来定义像素点对聚类中心的隶属度,表示像素点xj到第i类的距离,表达式为dij=‖xj-ci‖,表示为欧几里得距离。
为求得目标函数极小值min{J(U,C)},FCM聚类算法如下:
1)设置聚类数目K(2≤K≤N)与隶属度函数m,初始化模糊聚类矩阵U(n)的初始值。
2)计算C(n):
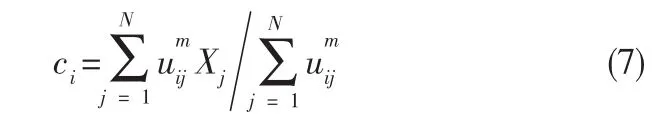
其中,j∈[1,K]。
3)由U(n),C(n)和

计算出U(n+1).
4)设置迭代终止阈值α,计算‖U(n+1)-U(n)‖的值,若其大于阈值α,则继续重复上述步骤,否则迭代停止。
对于任意个像素,选择其模糊聚类矩阵中的最大值并将其标记为k类,对于图像中所有像素进行这一操作,完成对图像的分割。
2.2 改进FCM分割算法
虽然FCM算法已经成功的应用于各种类型的图像分割领域,但是这种算法容易陷入局部最优,分割的正确与否与初始点的选择有很大关系,并且计算量巨大。针对以上问题,提出一种根据PCNN最短路径的FCM算法,快速准确的完成钢带裂纹分割。
在图像中,两点之间的相连关系不仅可以通过像素的灰度值得以体现,而且还可以通过像素之间的最短距离确定。在钢带表面缺陷图像中,缺陷可能存在不同区域,像素的8邻域不能够很好地体现这种相关性,设置一个M×M的邻域,定义公式(9)的边权,更好地反映邻域像素之间的时间复杂度和相互影响度。通过1.2节改进的PCNN算法计算中心点与所划分的邻域个点的最短距离,用以表达它们之间的相关性。

其中,f表示像素灰度值,β表示分属两个不同类的阈值,‖·‖表示两像素的欧氏距离。
经典FCM算法需要在计算之初给定初始聚类中心,并且初始聚类中心的选取对于分割效果影响很大,针对人工设置聚类中心自适应能力差的问题,采用有效性指数的方法自适应确定。虽然在钢带表面缺陷图像中,缺陷区域和背景灰度差别较小,但是一定存在一个边界点,此边界点的特征和区域内像素的特征具有较强的相关性,为了加强区分度,可以通过图像的显著性对图像进行预分割,其目的是提高不同区域的区分度,降低同一区域内像素点的差别。因此,图像的初始聚类中心可以通过图像不同区域边界的灰度值分布来估计,如公式(10)所示:
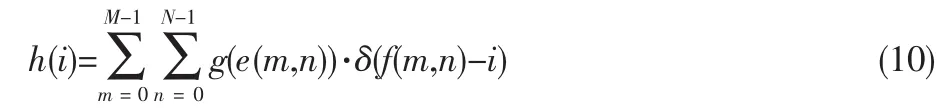
其中,e(m,n)表示图像像素f的局部特征,g(·)是其局部特征函数。
2.3 本文算法流程
以下是基于PCNN最短路径FCM的钢带表面缺陷分割步骤,流程图如图2所示。
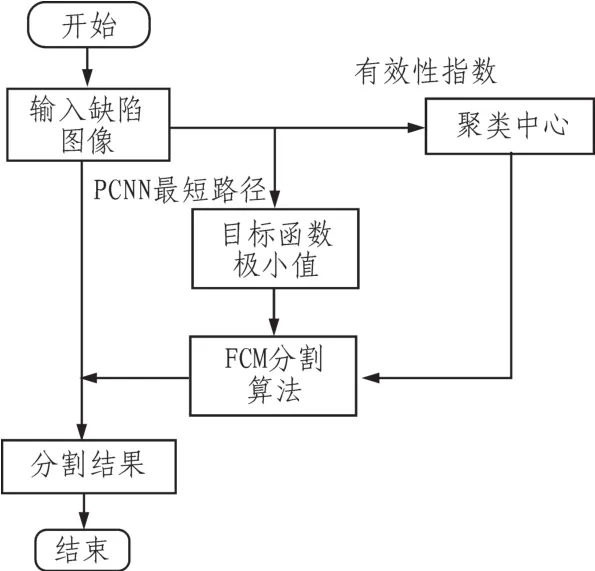
图2 本文算法流程图Fig.2 Flow chart the algorithm
1)初始化相关阈值,通过有效性指数h(i)自适应求得初始聚类中心;
2)通过计算得到的U(n),U(n+1)矩阵,通过PCNN最短路径算法快速确定目标函数极小值min{J(U,C)};
3)通过目标函数极小值对钢带表面缺陷图像进行缺陷目标分割。
3 实验与结果分析
为了验证本文算法的有效性,在配置为:2.5 GHz四核CPU,4 GB内存,系统为Windows 7旗舰版,软件环境为Matlab 2010b的测试平台上编程通过,分别与经典FCM算法、文献[8]的算法进行比较。试验中,所采用的图像大小均为256×256的灰度图像。上述算法处理结果如图3所示。

图3 不同算法分割比较Fig.3 Segmentation for images by different algorithms
为了进一步验证本文算法的优越性,选取100张夹杂缺陷图片、100张异物压入缺陷、100张擦划伤缺陷图片,分别进行横向对比测试,实验结果如表1所示。

表1 三种分割算法对比评估Tab.1 Assessment of algorithms
可以看出,本文算法对各类缺陷都能保持较高的识别率,对于未能100﹪识别,主要原因在于有些缺陷过于轻微或钢板上粘有杂质,造成了误判。经典FCM算法对于本文中的图像适应能力较差,容易将噪声和缺陷目标分割在一起,文献[8]的算法虽然能够较好的分割缺陷目标,但是运算时间长,不能够满足实时在线监测的需要。
4 结论
由于钢带表面缺陷复杂多变,传统目标分割算法难以满足需要,因此本文提出一种基于PCNN最短路径的FCM快速钢带表面缺陷算法,该算法通过有效性指数自适应求得FCM初始聚类中心,然后通过改进的PCNNN最短路径算法快速比较确定FCM目标函数极小值,最后通过得到的目标函数极小值矩阵,分割出缺陷目标。
实验结果表面,本文算法的适应性和正确率都较高。如何在光照变换复杂的情况下正确分割缺陷目标,是本文下一步研究方向。
[1]罗新斌,康戈文.基于统计学习背景模型的钢带表面缺陷分割[J].仪器仪表用户,2007,14(5):106-107.LUO Xin-bin,KANG Ge-wen.Surface defects inspection of metal strips based on Statistical learning background model[J].Electronic Instrumentation Customer.2007,14(5):106-107.
[2]梁文豪.基于机器视觉的带钢表面缺陷识别研究[D].武汉:武汉科技大学,2010.
[3]谭绍华.基于机器视觉的带钢表面缺陷检测系统研究[D].武汉:华中科技大学.2012.
[4]Kumar A,Pang G.Identification of surface defects in textured materials using wavelet packets[C].Conference Record-IAS Annual Meeting,2001(1):247-251.
[5]Borselli A,Colla V.Surface defects classification in steel products:A comparison between different artificial intelligence-based approaches[C].Proceedings of the 11th IASTED International Conference on Artificial Intelligence and Applications,2011:129-14.
[6]郑皓天,顾晓东.基于带宽剩余率的脉冲耦合神经网络最短路径算法[J].系统工程与电子技术,2013,35(4):859-863.ZHENG Hao-tian,GU Xiao-dong.PCNN shortest path algorithm based on bandwidth remaining rate[J].Systems Engineering and Electronics,2013,35(4):859-863.
[7]Zhao Zaixin,Cheng Lizhi,Cheng Guangquan.Neighbourhood weighted fuzzy c-means clustering algorithm for image segmentation[J].Image Processing,2014,8(3):150-161.
[8]徐少平,刘小平,李春泉,等.基于区域特征分析的快速FCM图像分割改进算法 [J].模式识别与人工智能,2012,25(6): 987-995.XU Shao-ping,LIU Xiao-chun,LI Chun-quan,et al.An improved fast FCM image segmentation algorithm bsed on regin feature analysis[J].Pattern Recognition and Artificial Intelligence,2012,25(6):987-995.
Surface defects inspection of metal strips based on PCNN and FCM
KANG Kang
(Baoji University of Arts and Sciences,Baoji 721016,China)
For there is no better way to detect the defects of metal strip accurately,it presents a new algorithm based on improved pulse coupled neural network(PCNN)and Fuzzy C-means(FCM).Firstly it can be obtained a clustering center through the effectiveness index.Secondly,through the PCNN shortest path algorithm,the objective function minimum values was determined.Finally,it can be detected the defects of metal strips by improved FCM.By the comparison Experiments,it shows that this algorithm can rapidly detect the defects,the proposed method can increase segmentation accuracy rate to 95﹪.
defect inspection;the shortest path;pulse coupled neural network(PCNN);fuzzy clustering
TN919.8
:A
:1674-6236(2015)18-0061-04
2015-02-02稿件编号:201502003
宝鸡文理学院校级重点项目(ZK14087)
亢 伉(1987—),男,陕西宝鸡人,硕士,助教。研究方向:机器视觉、人工智能。

