琼北乡村聚落边界形状的量化研究

谢 丹，裴保杰，杨定海

(海南大学 园艺园林学院，海南 海口 570228)

SI1=P/A，

SI1权均=SI1 小×0.642 7×0.25+ S中×0.5+SI1 大×1.560 8×0.25 .

，

SI3=2lnP/lnA ，



琼北乡村聚落边界形状的量化研究

谢 丹，裴保杰，杨定海

(海南大学 园艺园林学院，海南 海口 570228)

以琼北地区的20个传统乡村聚落为研究样本，运用图底分析的方法，借助景观生态学中的3个斑块形状指数：即图形的周长面积比SI1、图形周长与等长宽比等面积的椭圆周长之比SI2和景观分维数SI3分别对样本进行量化分析，结果表明：采用分维数SI3先对聚落边界图形进行初步筛分排序，然后再结合图形外接矩形(弧形)的长宽比和形状指数SI2进行进一步的分析，可以更全面地了解图形的复杂性和破碎度，并且可应用此方法来研究琼北地区乡村聚落的形态特征.

传统聚落； 边界图形； 形状指数； 量化分析

传统聚落的聚集过程是一个随机性的自组织过程，因而聚落的形状呈现出非线性特征.在聚落的聚集过程中，受到聚落的地形地貌、环境意识、宗族观念等内外因素的共同影响，各个乡村聚落自适应地选择合适的生长方式，聚集形状呈现出不同的特点.

本文以琼北地区20个传统聚落为研究对象，应用三个斑块形状指数定量分析聚落形态特征，以寻求最佳量化分析的方法，并将这种方法应用于对琼北20个传统聚落的形态研究中.

1 琼北乡村聚落简介

1.1 研究范畴界定 琼北地区的地理范围在学界上并没有一个明确的界定，根据不同的分类依据，其范围也各不相同.本文以区域为界，界定琼北地区为海口、文昌、琼海、定安、澄迈5市县，其人群构成、地形地貌、聚落群体结构等相对都比较接近，以便更深入的研究琼北地区乡村聚落空间形态的特点.

1.2 研究区概况 海南岛的地貌呈穹窿状，中间高四周低，其地势从中部山体向外，按山地、丘陵、台地、阶地、平原的顺序逐级递降，构成层状垂直和环状水平分布.[1]琼北地区位于海南岛圈层式阶梯状地形结构北缘，多平原滩涂.琼北地区属雷州地洼列，研究区内的琼北火山覆盖面积广，具有陆相和海相的双重特征，造就了琼北地区乡村聚落独一无二的地理环境.从气候特征看，研究区地处热带北缘，属热带季风气候，全年暖热，“四时常花，长夏无冬”，雨量充沛，常风较大，台风频繁.主要居住人口为汉人，人口密度较大，自古以来属于海南岛相对开化较发达的地区.

琼北地区这种特殊的地貌特征、历史条件和热带海洋性气候等因素协同影响，形成了琼北地区独特的聚落结构.

2 传统聚落边界闭合图形的设定

本文综合参考王昀教授所借鉴佐藤方彦的《人间工学基准数值数式便览》中日本人所表现出的个人之间距离关系的研究和杨·盖尔引用的T·霍尔的《隐匿的尺度》中的数据，借鉴浦欣成教授著的《传统乡村聚落平面形态的量化方法研究》中关于乡村聚落三种不同的虚边界尺度的定义方法，并结合琼北地区传统聚落的基本情况，设定了7 m、30 m以及100 m三个层次的边界尺度.7 m，是日本人所言之“相互认识域”内的“近接相”范围(3～7 m)与“远方向”范围(7～20 m)的分界点；30 m，人的面部特征、发型和年纪都能看得见，不常见面的人也能看得出，而这也是日本人所言之“识别域”内的“近接相”范围(20～35 m)；100 m，是社会性视域的最高限，能够分辨出具体的个人，但是无法明确对象或者明晰对方行为活动.[2]

以琼海市加积镇排岭村为例设定一个聚落的边界图形.

① 处理聚落总平面图

运用图底分析方法，将聚落中的建筑物和墙体作为实体，在原始CAD图上，把建筑物和墙体涂成黑色，而把外部空间留白.得到一张纯粹以建筑和墙体为要素的聚落空间图斑(图1).

② 设定以7 m为虚边界尺度的聚落小边界

以聚落最外缘的建筑单体转角顶点为基点，绘制边界的连接线(连接线不能穿越建筑物实体)，形成闭合图形，将聚落所有的建筑包围于闭合图形内.边界线是以建筑单体的实边界与建筑之间的虚边界构成，虚边界在不同层级的聚落边界中绘制标准各不相同[3].小边界即是将各外缘建筑单体的转角顶点上跨跃式连接，单段连接线不大，于7 m(当建筑单体间隔大于7 m时，则取连接线最短)(图2).

③ 设定以30 m为虚边界尺度的聚落中边界

绘制原则与7 m小边界一致，将最大7m的跨跃距离增加到30 m，以聚落最外缘的建筑单体转角顶点为基点，即可得到聚落中边界.

④ 设定以100 m为虚边界尺度的聚落大边界

绘制方法同小边界和中边界一样，将最大跨跃距离增加到100 m.

图2 排岭村总平面的小、中、大三层边界图

⑤ 叠合三层边界

将小边界、中边界和大边界图层叠加在同一张图上，形成三层边界的叠合图.

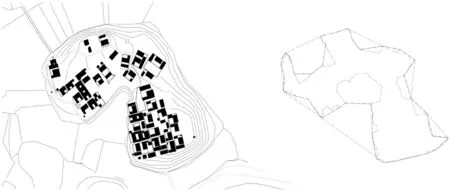
图3 琼海排岭村边界叠合图

3 传统聚落边界闭合图形形状的量化分析

聚落边界闭合图形是一个平面二维图形，对于该几何图形形态特征的研究，目前并没有一个广泛使用的方法.以图形的周长和面积的关系来估算是比较容易计算的.本文通过借鉴2种形状指数和分维数来分析琼北地区聚落边界图形特征，对比分析其结果，以期获得一个合理的方法对聚落边界图形进行量化分析.

大、中、小三层边界层层收缩，其中以中边界更为精确，它不会像大边界般粗略，也没有小边界的琐碎，其尺度更符合乡村聚落的空间尺度.因此本文在进行形状指数和分维数的加权时以中边界形状指数SI中为主，以SI小和SI大对数据进行适当修正，因此分别以25%、50%和25%的加权计算小、中、大边界图形形状指数平均值.

3.1 周长面积比SI1

SI1=P/A，

(1)

其中，P为边界图形的周长，S为边界图形的面积.

通过计算，统计出琼北20个样本聚落的周长面积比SI1，三层边界的平均值分别为SI1小(均)= 0.045 9，SI1中(均)=0.029 5，SI1大(均)=0.018 9.SI1小(均)明显大于SI1大(均)，若直接采用这些原始数据进行加权平均，SI1小的权重势必大于SI1大.因此，本文将借助SI1中对小边界形状指数SI1小和大边界形状指数SI1大进行转换，以减小误差.

SI1中(均)/SI1小(均)= 0.029 5/0.045 9=0.642 7,SI1中(均)/SI1大(均)= 0.029 5/0.018 9=1.560 8

于是，借助SI1小×0.642 7,SI1大×1.560 8，使二者都转换到中边界的数值尺度.

因此，本文设定的边界图形的加权平均指数公式：

SI1权均=SI1小×0.642 7×0.25+S中×0.5+SI1大×1.560 8×0.25 .

(2)

3.2 形状指数SI2 斑块形状指数SI2是景观生态学中常用的景观指数之一，通常是经过某种数学转化的斑块边长与面积之比.常用结构紧凑而又简单的形状(圆、正方形或长方形等)的形状指数作为参照标准[4].形状指数反映了斑块形状的复杂程度.形状指数越大，斑块形状图形越破碎.斑块形状的破碎度可能来源于图形狭长的长宽比，也可能由于图形本身的凹凸程度.为了能更准确地剖析乡村聚落的平面形态，本节采用长宽比λ和以等面积同长宽比的椭圆为参照的形状指数SI2两个指标进行分析.具体操作方法如下：

(1) 由聚落边界长宽比(λ)初步筛分

长宽比λ， 是指聚落边界外接矩形(弧形)的长短轴的比值，反映了聚落边界图形的狭长程度.比值越大，边界图形越狭长，其带状特征越强烈.

依次计算出20个样本村落边界图形的长宽比，并进行排序和特征筛分.在20个样本聚落的平面形态中，排岭村等聚落的长宽比λ小于1.5，聚落形态显示为明显的团状特征；从皇坡村等聚落开始，长宽比λ大于1.5，聚落形态呈现带状倾向，而从燕山内村到岭头村，长宽比λ大于2，聚落呈明显的带状.因此，本文以λ=1.5和λ=2为临界点，对聚落进行初步分类(表1)：

表1 20个样本聚落边界图形的类型初步筛分表

(2) 由形状指数进一步量化

① 形状指数SI2

本节选择与聚落各层边界等面积同长宽比的椭圆作为参照图形，形状指数公式为：[5]

(3)

其中，P为边界图形的周长，A为边界图形的面积，λ为图形外接矩形(或外接弧形)的长宽比.

② 加权形状指数

根据公式(3)，计算出20个乡村聚落的三层边界形状的形状指数，小边界形状指数平均值SI2小(均)=2.498 1，SI2中(均)=1.629 9，SI2大(均)=1.202 5.借助SI2中对小边界形状指数SI2小和大边界形状指数SI2大进行转换，以减小误差.

SI2中(均)/ SI2小(均)=1.629 9/2.4981=0.652 5,SI2中(均)/ SI2大(均)=1.629 9/1.202 5=1.355 5

于是，借助SI2小×0.652 5,SI2大×1.355 5，使二者都转换到中边界的数值尺度.

因此，本文设定的边界图形的加权平均指数公式为

SI2权均=SI2小×0.652 5×0.25+SI2中×0.5+SI2大×1.355 5×0.25 .

(4)

3.3 分维数SI3 分维数是以景观斑块的周长和面积的关系来分析斑块的破碎度.基于斑块的周长与斑块的面积的相关性，分维数的数值一般在1～2之间.分维数越大，斑块平面越不规则，斑块结构的破碎程度越高；分维数越趋近于1，则斑块的几何形状越简单.分维数的计算公式为[6]

SI3=2lnP/lnA，

(5)

其中，P为边界图形的周长，A为边界图形的面积.

4 讨 论

4.1 关于形状指数

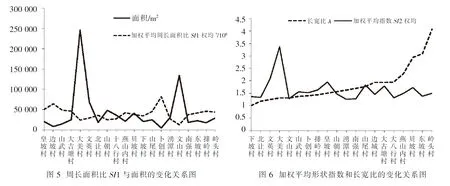
根据以上三种指数得出的样本聚落的数据统计结果，分别构建20个样本聚落的形状指数和分维数的变化关系图.由于SI1数值与图形面积的数值相差太大，此处将SI1数值乘以106，将其转换到图形面积的尺度，使得SI1的变化趋势更易于观察.作出SI1*106与聚落中边界图形面积的关系图(图5).由图可知，SI1与聚落面积呈显著的负相关，聚落面积越大，其周长面积比SI1数值越小.而数据对于图形的复杂程度敏感度差，无法反映出图形的形态特征.

SI3用以描述边界图形形状的复杂性，其数值越大，即表示边界图形越复杂.从图7可看出，分维数基本能准确地反映出20个聚落的平面形态的复杂程度，是一个较好的指数.但是，分维数SI3可对样本的复杂程度进行一个初步排序，不能明确反映出边界图形破碎原因.

利用长宽比λ可准确反映聚落边界图形的狭长程度，再根据形状指数SI2的数值大小，可以得出图形本身的边界曲折程度(图6)，通过这两个指标可以科学、理性的描述聚落边界图形的二维平面形态特征.因此，长宽比λ和形状指数SI2相结合适合用于研究聚落边界图形的破碎程度.由图7可知，大美村的分维数较高，而从图6可看出，大美村边界图形的破碎度主要来源于图形自身的凹凸程度.而岭头村较高的分维数则主要是因为其狭长的长宽比.

综合以上分析可知，采用分维数SI3对聚落边界图形进行筛分排序，然后结合图形外接矩形(弧形)和形状指数SI2进一步分析，可以更客观整体地了解图形的复杂性和破碎度.

4.2 琼北地区传统聚落边界图形的特征

4.2.1 琼北地区传统聚落边界图形的特征 由计算结果可知：加权平均形状指数S权均在以1.630 0为均值的数值区间1.251 3～3.372 0内，长宽比λ在以1.833 9为均值的1.000 3～4.070 6数值区间内，其中λ在1～1.5之间有10个样本聚落，1.5～2之间有6个，长宽比λ大于2的聚落有4个.

1)边界形状

(1)团状

由表1可知，团状聚落村庄数量较多，占样本的50%，聚落规模大小不一，多分布在地势较平坦的平原地区.团状聚落整体布局紧凑，聚落核心明确.根据聚落形态的主要影响因素，可将团状聚落归纳为以下三种类型：

① 聚落单体组织受某种规划理念诱导(宗族观念、环境意识等)，如下坡村、北让村.这类村落往往由同姓族群构成，且多由闽粤一带移民过来，宗族意识较强，聚落规划体现出一定的宗族观念，建筑布局紧凑规整，呈典型的梳式布局.

② 聚落布局围绕某一中心层层展开，呈向心式，如文英村、大美村.聚落样本中部分聚落位于琼北羊山地区，水资源紧张.因此，水塘、水井往往就成为聚落生长的核心.这种布局模式既吻合中国古代风水理念，也符合羊山地区的自然环境条件.

③ 聚落受到地形、气候等因素的影响，聚落用地被限制于某一集中地块内，如文山村、排岭村.文山村三面环水，聚落格局受地形限制，村落房舍布局紧凑，形态呈团簇状.海南雨量丰富，有的聚落为避免洪涝灾害,往往选址在地势较高的地基集中居住，而高微丘高地面积有限，聚落呈团状布局，如排岭村.

图8 团状聚落平面图

(2)带状倾向的团状

带状倾向的团状聚落是团状聚落沿着一个方向外延扩展而成，是团状聚落横向生长的结果.聚落建筑单体沿着某一线形要素展开生长，聚落呈矩形特征.如山朝村、湧潭村等.

图9 带状倾向的团状聚落平面图

(3)带状

岭头村、东坡村和贝坡村的长宽比λ数值最高，分别为4.070 6、3.093 8和2.946 4，其数值远大于图形形状的临界点2，表明岭头村和东坡村带状特征强烈.从其平面图形可知，聚落形状属于弧带型，但它们形成机理不尽相同.东坡村位于琼海乐城岛边缘，其边界形状随岛的边缘而呈弧形；贝坡村顺应贝坡河的河岸形成带状的布局空间；岭头村则是位于山谷中，聚落建筑单体沿山体等高线布局而成弧带状.聚落沿道路、河岸、等高线布局而呈现带状特征，因此带状聚落的形成主要是受自然因素的影响.

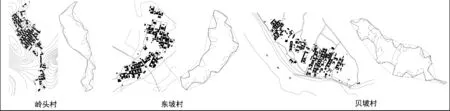
图10 带状聚落平面图

2)边界图形破碎度

(1)平滑简单的边界

湧潭村、南强村、文山村的形状指数SI2较低，依次从1.251 3、1.279 8、1.285 1逐渐升高，这些聚落边缘空间建筑单体之间距离小或排列比较平直整齐，从而减少了边界图形的凹凸尺度，使得形状指数数值较低.琼北地区聚落边界图形平滑简单的类型主要可分为以下两种：

① 当聚落的边界遇到无法逾越的自然阻碍时，如山体、道路或水系等，聚落边界临近阻碍一侧无法自由生长，形成停滞的边界，因此临近阻碍一侧的建筑组织具有较高的秩序感和密实度.如文山村三面环水，聚落建设用地受水系分割，环绕的水系清楚的界定了聚落形态，聚落边缘建筑紧凑，聚落边界图形平滑.南强村则是受到道路和山体的双重制约，聚落缘空间建筑单体之间距离小，因此其形状指数较低.

② 同姓族群聚集聚落，聚落在营建过程中遵从宗族理念，建筑布局规整，村落核心较明确，街巷网络也多规整清晰，聚落边界明确，因此其边界图形较为平滑简单，形状指数较低，如湧潭村、北让村和山朝村等.

(2)破碎复杂的边界

大美村、文英村和皇坡村的形状指数较高，分别为3.372 0、2.079 5和1.958 0，表明这些乡村聚落形状较复杂，不规则，住宅分布比较破碎，呈自然随机分布态势较强；其中大美村和文英村聚落核心部分密度较大，排列规则，但聚落外围建筑分布散乱，打破了聚落原有的紧凑结构，致使其形状指数较高.

琼北地区的传统聚落在选址时已经注意隐蔽性，将村落掩映在密林之中，往往是“不到村口不见村”，村口以蜿蜒小路入村，极大的增强了安全性.因此聚落自身的防御性不需要太强，防御体系以经济为主.其防御系统大多较生态自然，其形式主要为草灌林、是用火山石堆砌的低矮石墙，极少砌筑高墙围合村落.聚落边界的形态相对模糊尤其是聚落中村民自建的厕所、蓄养建筑，大多分布在聚落外围，远离居住建筑，且距离远大于本文设定的最小虚边界7 m的尺度，使得聚落边界形态更为模糊，致使聚落边界的形状指数升高.因此，生态自然的防御系统和村落边缘散乱的构筑物是导致琼北地区传统聚落破碎复杂的主要因素.

其次，聚落地区部分聚落为异姓聚居，由于聚落成员之间无血缘关系，宗族意识弱化，聚落凝聚力较弱，聚落形态较为松散.因此聚落内建筑之间距离较远，聚落边界图形较为破碎复杂.因此，聚落边界复杂程度与聚落的人口构成也有莫大的关系.

概而言之，聚落边界的破碎度主要受自然因素和文化因素的双重影响.

3)村落边界形态与建筑构造类型

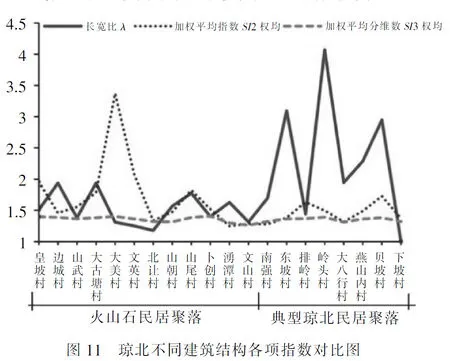
本文所选取的海口、定安和澄迈的聚落样本都处于是火山喷发后的熔岩地区，是火山石传统民居；而文昌、琼海的聚落样本则是典型的砖木结构的琼北民居.由图11的数据对比显示，两种类型的村落边界的各项指数没有实质性的差异，即表示建筑材料对聚落边界图形的形状和凹凸程度影响不大.也从某种意义上说明火山石传统民居是琼北民居的一种类型，是琼北民居和火山石文化共同融合演变而成的一种民居形式.[7]

4 结 语

以往对聚落形状的研究，大多偏重于归纳、分类的定性研究，定量分析甚少.本文通过对琼北乡村聚落边界形状指数的分析，得出合理的量化分析方法.并应用此方法，得到琼北地区传统聚落边界图形特征的基本数据.在此基础上，归纳总结琼北地区传统聚落边界图形的特征及其影响因素.

1) 采用分维数SI3对聚落边界图形进行筛分排序，然后结合图形外接矩形(弧形)和形状指数SI2进一步分析，可以更全面地了解图形的复杂性和破碎度.

2) 琼北地区传统聚落边界图形的特征包括边界图形的形状和边界图形的破碎度.而文化的聚集力量与自然的干预力量的相互耦合决定了琼北地区传统聚落边界特征.

(1) 形状

利用聚落边界图形外接矩形(弧形)对聚落的平面形态进行分类：

当λ≤1.5时，为团状聚落

当1.5<λ≤2时，为带状倾向的团状聚落

当λ>2时，为带状聚落.

据聚落形态的主要影响因素，团状聚落归纳为以下三种类型：

① 文化因素主导——聚落单体组织受某种规划理念诱导(宗族观念、环境意识等)，建筑布局紧凑规整，呈规整的梳式布局.

② 自然因素糅合文化因素——聚落布局围绕某一中心层层展开，呈向心式.

③ 自然因素主导——聚落受到地形、气候等因素的影响，聚落用地被限制于某一集中地块内.

带状倾向的团状聚落是介于团状聚落和带状聚落的一种过渡形态.

带状聚落的形成主要是受自然因素的影响，聚落沿道路、河岸、等高线布局而呈现带状特征，是团状聚落横向生长的结果.

(2) 破碎度

① 平滑简单边界形成原因

聚落生长受地形限制.聚落的边界遇到无法逾越的自然阻碍时，如山体、道路或水系等，聚落边界临近阻碍一侧无法自由生长，临近阻碍一侧的建筑组织具有较高的秩序感和密实度.

② 破碎复杂边界形成原因

a.琼北地区传统聚落的防御系统生态自然及村落边缘散乱的构筑物

b.异性聚居的聚落宗族意识弱化，聚落形态松散.

3) 通过对火山石传统民居与典型的砖木结构的琼北民居两种类型聚落的边界图形比较发现，建筑材料及建筑构造类型对聚落边界图形特征影响不大.

[1] 袁建平.海南岛地貌分区和分类[J].海南大学学报自然科学版,2006,24(4):364-370.

[2] 王昀.传统聚落结构中的空间概念[M].北京:中国建筑工业出版社,2009:60.

[3] 浦欣成.传统乡村聚落平面形态的量化方法研究[M].南京:东南大学出版社,2013:42.

[4] 邬建国.景观生态学：格局、过程、尺度与等级[M].北京:高等教育出版社,2007:107.

[5] 浦欣成.传统乡村聚落平面形态的量化方法研究[M].南京：东南大学出版社,2013:67.

[6] 刘灿然.陈灵芝.北京地区植被景观中斑块形状的指数分析[J].生态学报,2000,20(4):559-567.

[7] 中华人民共和国住房和城乡建设部.中国传统民居类型全集[M].北京:中国建筑工业出版社,2014:369.

Quantitative Research on the Spatial Form of Rural Settlement in Northern Hainan

Xie Dan, Pei Baojie, Yang Dinghai

(College of Horticulture and Landscape Architecture, Hainan University, Haikou 570228, China)

In the report, 20 Rural settlement in Northern Hainan were used as the research samples, based on three landscape ecology patch shape index, the ratio of perimeter to inner area (SI1), the ratio of shape perimeter to the perimeter of a ellipse with equal aspect ratio, equal area with the shape (SI2), and the landscape fractal dimension (SI3), the figure-ground diagram method was used for the quantitative research. The results showed that fractal dimension (SI3) was used for the preliminary analysis of the boundary shape settlement, and then, combined with aspect ratio of the external rectangular (arc) and shape index (SI2), the further analysis were performed, which can be more comprehensive for the understanding of the complexity and fragmentation of the graphics, and which can be applied for the analysis of the morphological characteristics of rural settlements in northern Hainan.

traditional settlement; boundary shape; shape index; quantitative analysis

2015-03-01

国家自然科学基金资助(51468015)；海南省自然基金项目(311037)；海南大学青年基金项目(qnjj1249)

谢丹(1990-)，女，湖南永州人，海南大学园艺园林学院2012级硕士研究生，E-mail:707097904@qq.com

杨定海(1975-)，男，陕西宝鸡人，副教授，硕士生导师，研究方向：景观生态学，E-mail: 275886568 @qq.com

1004-1729(2015)03-0277-09

TU 986.1

A DOl：10.15886/j.cnki.hdxbzkb.2015.0050