数学娱乐(十六)——移棋相间问题与国际科研成果

耿 济

(海南大学，海南 海口 570228)

○○○●●●

—— ○●●●○○

○●●——○●○

——●○●○●○

○○○○●●●●

○——○●●●●○○

○●●○——●●○○

○●●○●○●——○

——●○●○●○●○

○○○…○●●●…●——

——●○●○●○…●○

●(一)○(二)●(三)○(四)●(五)○(六)，

一二三四 五六七八九十

○○○●●●

一二三四五六七八九十

●○●○●○

●○● ○○●

●●○○○●

○○○●●●

··A B A B A B A B

(1) B A A B A B A · · B

(2) B A A B · · A A B B

(3) B · · B A A A A B B

(4) B B B B A A A A

——○●○●○●…○●

●●●…●○○○…○——

○○○…○●●●…●——

⋮ ⋮ ⋮

——● ○… …●○●○

——● ○ ● ○…● ○ ● ○

⋮ ⋮ ⋮

○ ○ ○ … ○|●…● ● ●——

——○ ● ○ ●…○ ●○ ●

⋮ ⋮ ⋮

● ● ●…● ○ ○ ○…○ ——

a1a2a3a4…anbn…b4b3b2b2——，

——b a b a…b a b a，

(○○○(○●●a4)-D(——●a4)，



数学娱乐(十六)
——移棋相间问题与国际科研成果

耿 济

(海南大学，海南 海口 570228)

全文分2部分.第1部分是移棋相间，第2部分科研成果.

移棋相间； 逆命题； 科研成果

本文是数学娱乐系列文献[1～15]的续作.

日本著名数学史家平山谛著《东西数学物语》一书，叙述日本鸳鸯游戏和英国泰特问题时指出[16]：“也许到日本明治时期后，由于日本和西方频繁的交通来往，这个游戏自然地从日本传到了西方，至今在中国文献中也没有发现类似游戏”.因此国际上误认为这一游戏起源于日本，事实上，最早的文献记载是中国，称为移棋相间。

本文目的分为2部分，第1部分主要是移棋相间问题有关史料，第2部分是移棋相间的国际科研成果.

1 移棋相间问题

中国围棋源远流长，棋子分黑与白2色.清代顺治年间(1641年—1661年)胡砺之利用黑色和白色棋子进行下述游戏.

首先，把3个相连白子与3个相连黑子排成一行，每次移动相邻两子，进行3次移动得到

○○○●●●

—— ○●●●○○

○●●——○●○

——●○●○●○

出现黑白相间的现象.

接着，把4个相连白子与4个相连黑子排成一行，每次移动相邻两子，进行4次移动得到

○○○○●●●●

○——○●●●●○○

○●●○——●●○○

○●●○●○●——○

——●○●○●○●○

出现黑白相间的现象.

最后，当5≤n≤10时，经过n次移动都有黑白相间的现象.

以上史料根据清代褚稼轩著《坚瓠集》(成书于康熙年间，即1662年-1722年)，摘录如下[17]：

“幼时见友人胡砺之将黑白棋子各三枚左右分列，三移则黑白相间.余因问曰：多亦可移乎，砺之曰：自三以至十外皆可移，多一子则多一移.余归试之，自三以至于十，果相间不乱.今已三十余年，偶雨窗复试，忘其大半，因绎数四始得就.”

近代学者俞平伯祖父俞曲园著《春在堂随笔》中有一段记载[17]：

“长洲褚稼轩《坚瓠集》有移棋相间之法，……，余试之良然，而内子季兰复推广之，自十一子以至二十子”.

由此可知，当11≤n≤20时也能出现移棋相间的现象.

很自然地对于这一游戏产生下面的猜想.

移棋相间问题 正整数n≥4时，把n个相连白子、n个相连黑子以及两子的空位排列成最初形式：

○○○…○●●●…●——

每次任意移动相邻两子(不得改变次序)到空位或新的空位上，那么存在着n次移动能使得黑子与白子相间的最后形式；

——●○●○●○…●○

接着叙述移棋相间在国外的情况.

日本文献中最早的记载是1743年中根法舳著《勘者御伽双纸》一书中的“鸳鸯游戏”[16]，抄录如下：

“黑白棋子各有三个，如图所示，按黑白相隔放置

●(一)○(二)●(三)○(四)●(五)○(六)，

问如何移动一处的每两个棋子的位置使它变为如○○○●●●之形式？

法曰：使四五移至七八，一二移至四五，三四移至九十，则成为

一二三四 五六七八九十

○○○●●●

图解这个过程如下：

一二三四五六七八九十

●○●○●○

●○● ○○●

●●○○○●

○○○●●●

因为把黑白棋子来回移动操作，就如鸳鸯朝夕相处，悠然自得地在水面上游泳那样的缘故，所以，就产生了‘鸳鸯游戏’的名称.”

欧洲文献中最早的记载是1884年英国物理学家泰特(Tait)在《哲学杂志》(Philosophical Magazine,1884,vol.5)上，他把4枚金币(设为B)和4枚银币(设为A)进行如下排列：

··A B A B A B A B

(1) B A A B A B A · · B

(2) B A A B · · A A B B

(3) B · · B A A A A B B

(4) B B B B A A A A

欧洲把上述问题叫做泰特问题.[16]

根据以上史料很自然地类似前面情况产生下面的猜想.

移棋相间的逆问题 正整数n≥4时，把n个白子和n个黑子加上两子的空位排列成白子与黑子相间的最初形式：

——○●○●○●…○●

每次任意移动相邻两子(不得改变次序)到空位或新的空位上，那未存在着n次移动使得黑子相连和白子相连的最后形式：

●●●…●○○○…○——

最后应该指出上述2个猜想之间的关系.

性质1 假设移棋相间问题成立，那么移棋相间的逆问题也成立，反之亦然.

证明 假设正整数n≥4时移棋相间问题成立，即从最初形式经过n次移动出现的最后形式如下：

○○○…○●●●…●——

⋮ ⋮ ⋮

——● ○… …●○●○

接着把第1行与第n+1行对调，类似地把第2行与第n行，第3行与第n-1行，…，依次分别进行对调后得到下述排列形式

——● ○ ● ○…● ○ ● ○

⋮ ⋮ ⋮

○ ○ ○ … ○|●…● ● ●——

最后再把所有的白子与所有的黑子对调，即得移棋相间的逆问题：

——○ ● ○ ●…○ ●○ ●

⋮ ⋮ ⋮

● ● ●…● ○ ○ ○…○ ——

反之亦然，证毕.

2 国际科研成果

1887年法国德兰诺伊(Delannoy H)首先证明了移棋间的逆问题，论文发表在《自然》杂志(La Nature,1887,vol.15)上[16].

对于任意正整数n≥4分为偶数与奇数2种情况.

当n≥4为偶数时，以n=12为例.

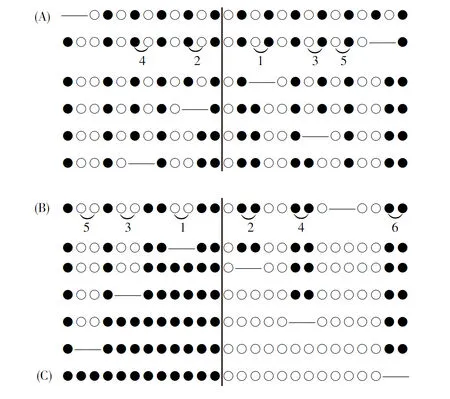
最初形式记为(A)，最后形式记为(C)，中间过渡形式记为(B).

首先从(A)的右边第2，3两子移至空位，如图所示左右分开，作奇、偶顺序号1，2，3，4，5，按照顺序移动2→1，3→2，4→3，5→4得到(B).再从(B)作前面相反的序号移动得到(C).

一般而言，作(A)的序号有如下规则：

作(B)的序号有如下规则：

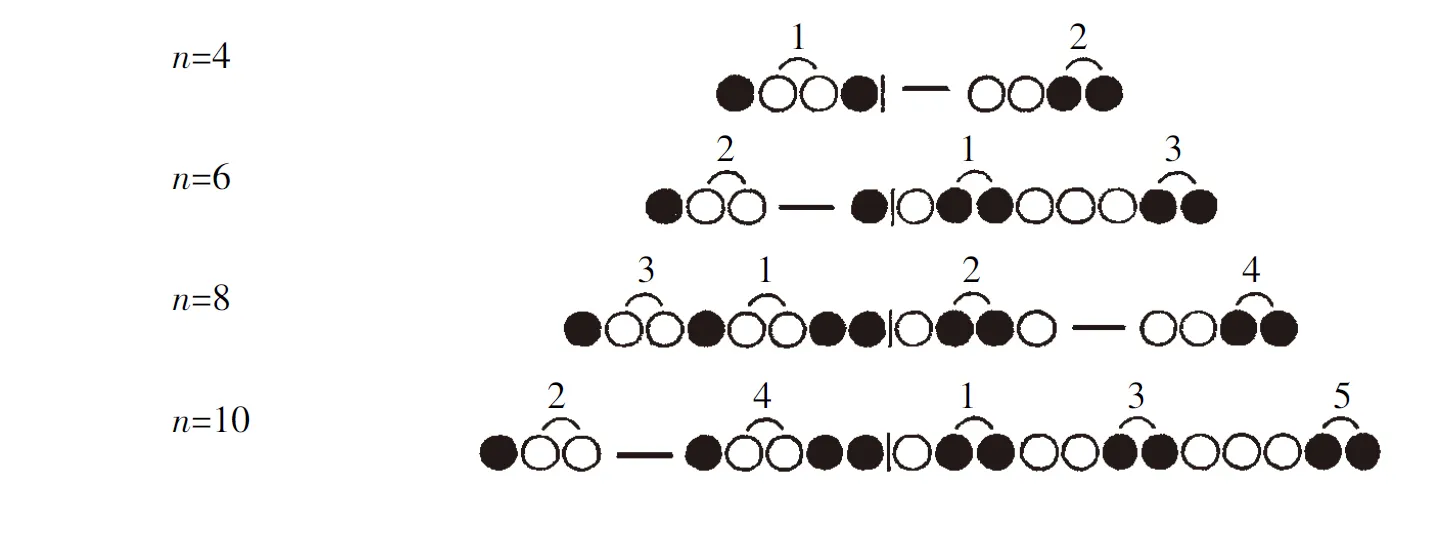
又当n≥4为奇数时，与前面偶数相同，只要改变如下的作序号的方法.

作(A)序号的方法：

作(B)序号的方法：

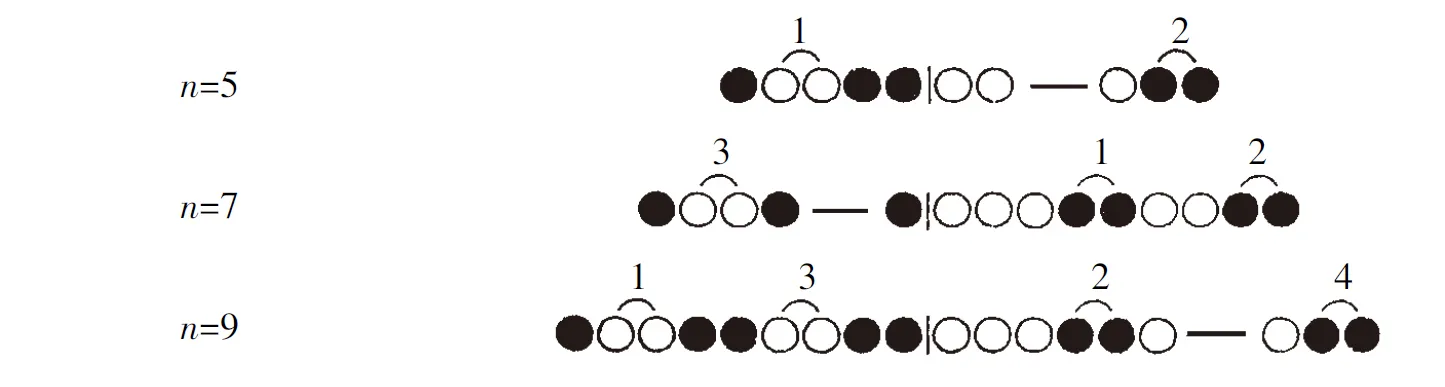
1899年日本林鹤一博士证明移棋相间逆问题的方法，以n=4，5，6，7成立的事实为基础，通过分别加边方法得出n=8，9，10，11；再从n=8，9，10，11分别加边方法得出n=12，13，14，15，如此继续下去，得出一般的证明.[16]

2010年中国耿济发表了移棋相间问题的证明[6].

首先，把最初形式表示为

a1a2a3a4…anbn…b4b3b2b2——，

经过n次移动后的最后形式表示为

——baba…baba，

其中ai(1≤i≤n)以及a代表白子“○”，bi(1≤i≤n)以及b代表黑子“●”.

在n次移动过程中发现存在[n/2]个始终有移动的棋子，它们的分布情况证明得到

简单情况，n=4，a4，b2;n=5，a4，b4;n=6,a6,b6,b2;n=7,a4,b6，b2.

一般情况，n≥8时，分为4种类型.

1)当n≡0(mod4)，即n被4整除时，就有a4,a8,a12,…，an-4,an;bn,bn-4,…,b12,b8,b2;

2)当n≡1(mod4)，即n被4整除余1时，就有a4,a8,a12，…，an-5,an-1;bn-1，bn-5,…,b12,b8,b4;

3)当n≡2(mod4),即n被4整除余2时，就有a4,a10,a14,…，an-4,an;bn,bn-4,…，b10,b6,b2;

4)当n≡3(mod4)，即n被4整除余3时，就有a4,a8,a12,…，an-3；bn-1，bn-5,…，b10,b6,b2.

其次，按照n次移动过程中始终没有移动的棋子把最初形式分割或[n/2]+1个小区间，类似地又把最后形式分割成[n/2]+1个小区间，这样每个小区间都有对应的小区间.

以n=8为例，按照a4,a8,b8,b2把最初形式分割成5个小区间(○○○a4),(a4○○○a8),(a8,b8),(b8●●●●●b2)，(b2●——)；又把最后形式分割成5个小区间(——●a4)，(a4●○●a8)，(a8,b8)，(b8○●○●○b2),(b2○●○).它们对应小区间(○○○a4)→(——●a4),(a4○○○a8)→(a4●○●a8)，(a8,b8)→(a8,b8),(b8●●●●●b2)→(b8○●○●○b2),(b2●——)→(b2,○●○).

由于移动的两子有4种可能情况，白白，黑黑，黑白，白黑，依次用A，B，C，D来表示，移出用记号“-”，移入用记号“+”.

现将以上5个小区间的移动过程叙述如下.

移动过程记为T1=(-A，+B，-D).

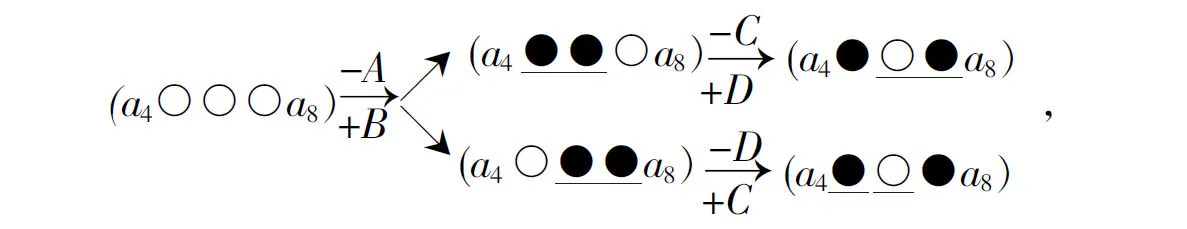
有2种移动过程记为T2=(-A+B-C+D)，T2′=(-A+B+C-D).(a8b8)→(a8b8)，移动过程记为T3=0

2种移动过程记为T4=(+A-2B+2C-D)，T4′=(+A-2B+C-C+D).

移动过程记为T5=(+A-C+D).

根据以上5个小区间上的移动结果得出：T1+T2+T3+T4+T5=0，T1+T2′+T3+T4′+T5=0.这里都是移出8次，移入8次的2种不同移法.

一般情况的4种类型按照以上方法进行论证[6].

最后，从最初形式左边和右边向中间分别移出A与B交替出现，即A→B→A→B→…共有[n/2]次；接着再从中间移出C或D，按照…→C→D→C→D，共有[n/2]+1次为止.

当n=8时的2种移法.

第1种移法a1a2…a7a8b8b7…b2b1——，经过A与B的4次移动为a2a3,b7b6,a5a6,b4b3，再经过C与D的4次移动b3a7，a6b5,b1a2,a1b7,得到——b6a4b4a6b5a8b8a5b1a2b3a7b2a1b7a3.

第2种移法a1a2…a7a8b8b7…b2b1——，前面4次A与B的移动为a2a3,b6b5,a6a7,b4b3,后面4次C与D的移动为b7a6,a5b4,b1a2,a1b6,得到——b5a4b1a2b3a8b8a5b4a7b7a6b2a1b6a3.

通过以上证明发现移棋相间及其逆命题的移法都不是唯一性.同时应该指出移动过程中没有移动棋子的分布也不是唯一性.以n=12为例，除了a4,a8,a12,b12,a8,b2外，还有a4,a8,a12,b6,b2;以n=14为例，除了a4,a10,a14,b14,b10,b6,b2外，还有a4,a8,a14,b14,b10,b2,一般情况请参考[6].

[1] 耿济.数学娱乐(一)——夫妻问题的新证与应用[J].海南大学学报(自然科学版)，2007，25(4)：321-324.

[2] 耿济.数学娱乐(二)——牙牌问题的新证与推广[J].海南大学学报(自然科学版)，2008，26(3)：206-219.

[3] 耿济.数学娱乐(三)——洛书定理与应用[J].海南大学学报(自然科学版)，2008，26(4)：303-308.

[4] 耿济.数学娱乐(四)——Nasik幻方的性质与构造法[J].海南大学学报(自然科学版)，2009，27(2)：107-115.

[5] 耿济.数学娱乐(五)——推广Fibonacci数列与幂级和[J].海南大学学报(自然科学版)，2009，27(4)：313-319.

[6] 耿济.数学娱乐(六)——移棋相间[J].海南大学学报(自然科学版)，2010，28(1)：1-10，14.

[7] 耿济.数学娱乐(七)——一个麻将和牌问题[J].海南大学学报(自然科学版)，2010，28(2)：93-98.

[8] 耿济.数学娱乐(八)——易经卦象的起源与考古发现的奇字[J].海南大学学报(自然科学版)，2011，29(2)：99-103.

[9] 耿济.数学娱乐(九)——学习《九章算术》的收获[J].海南大学学报(自然科学版)，2011，29(4)：297-304.

[10] 耿济.数学娱乐(十)——学习《九章算术》的收获[J].海南大学学报(自然科学版)，2012，30(2)：95-102.

[11] 耿济.数学娱乐(十一)——幻方与线性代数[J].海南大学学报(自然科学版)，2012，30(4)：299-305.

[12] 耿济.数学娱乐(十二)——广义华林公式与应用[J].海南大学学报(自然科学版)，2013，31(1)：1-7.

[13] 耿济.数学娱乐(十三)——类似华林公式的新公式[J].海南大学学报(自然科学版)，2013，31(2)：93-99.

[14] 耿济.数学娱乐(十四)——圆组合新概念与圆组合恒等式[J].海南大学学报(自然科学版)，2014，32(1)：1-7.

[15] 耿济.数学娱乐(十五)——从三角函数公式到伯努利数和欧拉数[J].海南大学学报(自然科学版)，2014，32(4)：295-301.

[16] 平山谛.东西数学物语[M].代钦，译.上海：上海教育出版社，2005：100-107.

[17] 姜长英.科学消遣[M].上海：科学出版社，1949，85-86.

Mathematical Recreation (ⅩⅣ):Problem of Move Pieces Become Black Alternation with White and International Achievements in Scientific Research

GengJi

(HainanUniversity,Haikou570228,China)

Thereportfallsintotwoparts,thefirstpartsisabouttheproblemofmovepiecesbecomeblackalternationwithwhite,andthesecondpartisabouttheachievementsinscientificresearch.

movepiecesbecomeblackalternationwithwhite;converseproposition;achievementsinscientificresearch

2014-11-28

耿济(1929-)，男，江苏镇江人，海南大学(退休)教授.

1004-1729(2015)03-0197-07

O 11

A DOl：10.15886/j.cnki.hdxbzkb.2015.0036