一种图像粒标记模型及其实现

李仲生,黄同成,蔡则苏

(1.邵阳学院信息工程系,湖南邵阳422000;2.哈尔滨工业大学计算机科学与技术学院,哈尔滨150001)

一种图像粒标记模型及其实现

李仲生1,黄同成1,蔡则苏2

(1.邵阳学院信息工程系,湖南邵阳422000;2.哈尔滨工业大学计算机科学与技术学院,哈尔滨150001)

针对图像分析领域缺乏可扩展的基础模型,对灰度图和彩图的标记模型展开研究。通过分析粗糙集和商空间理论的适用性,综合图像标记处理的特定应用需求,引出概念粒和连通粒2个概念,构建粒标记模型。基于通常情况下图像尤其是彩图标记中粒的数量巨大、结构复杂等现状,定义行连通段、潜在连通范围,引入动态预设标记集,简化连通判定,给出实现粒标记模型的线性算法,即图像粒标记算法。用二值图和彩图分别作验证和对比分析,结果表明,该标记算法有效、精确,且较传统标记算法更高速。

行连通段;连通粒;概念粒;图像处理;粒标记模型;图像粒标记算法

1 概述

已全面普及的图像摄制设备,迅猛发展的物联网,使得图像的数量爆炸式增长,给基于内容的图像检索带来了巨大的挑战。为加速图像的检索速度和精度,图像处理领域涌现出了一系列研究热点,例如显著对象提取、图像的语义标注等。分析这些热点方向产出的研究文献发现:处理的初始区域(或称基元)为全图、规则区域或某种图像分割结果。对于图像中潜在的语义对象而言,全图和规则区域与它除非碰巧相符(如一个图像中仅一个对象或一个对象正好和规则区域一样),否则没对应性。使用某种图像分割结果为基元与潜在对象间可能产生对应性,但处理速度会因为要分割图像而慢下来。因此,为进一步加快图像处理的精度和速度,寻找一种能与人类的思维方式有一致性、与潜在的语义对象有对

应性的基元是必要的,有益的。

粒计算(Granular Computing,GrC)是一个近些年来才凸现出的研究领域,是人工智能领域中的一种模拟人类思考和解决复杂问题的新理念和新方法［1］。这种模拟性使得粒计算理论对数据隐含语义的把握有着独具一格的能力,催生出了各具特色的众多成果。文献［2］提出了一种基于粒计算和云模型的彩色图像分割算法。文献［3］在文献［2］的基础上作了进一步的探索。文献［4］用粗糙集实现图像分割,文献［5］提出了一种粗糙集与mPCA相结合的人脸识别算法。文献［6］提出了一种基于模糊集的图像压缩技术。文献［7］利用粗糙集寻找区域语义分类。文献［8］述及了大量基于粒计算的研究成果,并展示了粒计算在图像处理领域的深入研究前景。这些成果涉及面广,对底层数据的隐含语义把握到位,可惜一般只针对特定应用,未形成简洁、高效和易于扩展的基础模型,因而难以被持续深入拓展和泛化、推广。针对这种情况,为表达出与语义对象有对应性的基元,给出基元生成的基础平台,本文参照粒计算理论,以粒作为基元,构建并实现一种图像粒标记模型。

2 图像粒计算模型

图像粒标记模型作为一种将二值图标记技术推广到一般图像(包括彩图)的基础平台,可用于显著对象发现、图像语义标注等几乎所有图像处理领域。

粒计算理论中的粗糙集理论模型［9］和商空间理论模型虽类似于孪生兄弟,但在具体应用中各有侧重:粗糙集理论主要用于表达数据、发现规则,而商空间理论常用于分析具有偏序(半序)关系的对象集问题。本文综合两者的优势,根据图像处理的特点,定义图像粒标记模型如下:

定义2(不可分辨关系,概念粒) 不可分辨关系是由任意属性子集B⊆A确定的一种二值关系,定义如下:

上述关系是容错关系。用不可分辨关系划分论域,将不可分辨的对象归入一类,得概念粒。概念粒的合集记为{AG［i］|i=1,2,…,n}(n为总数),满足以下约束:

定义3(连通关系,连通粒) 依据给定任意拓扑属性子集T⊆P,用式(3)判定连通关系:

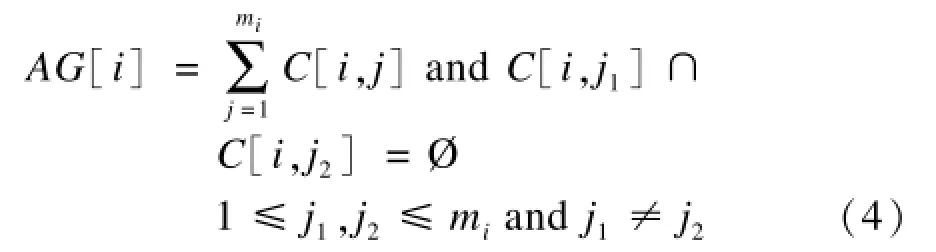
上文首先定义了拓扑信息系统,接着给出了其上的一种粒的统一形式化描述及对应约束,完成了图像粒标记模型的构建。下面依据图像粒标记模型,设计论证连通粒的获取和标记算法。

3 图像粒标记算法

3.1 图像连通区的标记

图像连通区标记是计算机视觉、图像理解、模式识别等领域中的基础工作之一。它赋给每个连通区一个唯一的标记,借此把图像转换成符号图,完成标记。标记研究目前只针对二值图或灰度图,已有大量研究成果。标记形成的方式上,这些成果可分为2类:(1)基于标记等价的算法,如文献［13］算法等,此类算法要做2轮或多轮光栅式扫描,由预设标记生成代表标记,完成后,再在最末一轮扫描中用代表标记替换相应的预设标记,完成标记;(2)基于搜索和扩展的算法,寻找一个未标记的前景点,赋予一个标记号,然后将此标记号扩展到所有与之连通的前景点,完成标记。

现有连通区标记算法存在局限性:只针对N×N或N×M的规则图,不适合标记任意形状、任意分布的连通区域;不能标记彩图;标记的结果为符号图,未提取记录各连通区,与图像中潜在对象的关系弱,不便于后续分析处理;标记速度仍有提升空间。针对这些情况,本文依据前文定义的粒标记模型,提出一种新的标记算法,即图像粒标记(Image Granule Labeling,IGL)算法。

3.2 IGL标记算法

定义4(行连通段) 一个概念粒在同一行上的连续象元构成的块,定义如下:

其中,r是行坐标;l为标记;s为列坐标的起点;t为相应终点;pn为指针,指向后继行连通段。初始行连通段中标记l被置为-1。对应的潜在连通范围和列坐标集如下。

定义5(潜在连通范围) 列坐标集,令k≥0,k,x为整数;sa=s-k;ta=t+k,则R的潜在连通范围为:ASR(r,s,t)={x|x≥saandx≤ta};列坐标集为:SR(r,s,t)={x|x≥sandx≤t}。

基于上述二定义,给出连通判定定义如下。

定义6(连通判定)R(y,s,t)在第y行,R(y1,s1,t1)处于第(y+1)行,如果ASR(y,s,t)∩SR(y1,s1,t1)≠Φ,则它们互相连通。当k=1时,八连通;k=0时,四连通。

定义6源于式(3),更利于实现,能极大地提升连通分析的速度。以下给出IGL算法标记和提取连通区的过程。

IGL算法仅需对图像做一次扫描。首先,提取一个概念粒的首行数据,将之视为当前行,记录行连通段,同时分别赋预设标记,记它们为临时连通区(即连通粒未提取完的中间结果,记为TCnw,下标n为概念粒号,w为相应的预设标记。所有在用的预设标记合成一个动态集W。接下来,提取下一行数据,记录行连通段,查找其中与当前行八连通的各行连通段。若当前行的当前行连通段在下行中没找到相连通的行连通段,跳过,处理当前行的下一个行连通段。若有,根据所找到的行连通段的标记l是否-1分别处理。若是-1,将它的标记改为w,加入对应于当前行当前行连通段的临时连通区TCnw。若非,则需进一步分2种情况:(1)l=w,意味着此前已加入过,不需再作处理;(2)l≠w,TCnw和TCnl将被合并为一个,设为TCnm,其中,m=min(l,w)。合并时,非m的标记将替换为m,同时,从预设标记集W中删除max(l,w)。

完成当前行所有行连通段的处理后,所有未找到后继行连通段的TCnw成为最终连通区,记为Cij(i是概念粒号,j=1,2,…是连通粒号),从W中删除w;同时,给下行中未被任何TC合并的行连通段赋预设标记,形成新的临时连通区。

处理完毕后,向前迭进,将下行设为当前行,它的后续行成为新的下一行,重复前述过程,直到一个概念粒的最后一行完毕。接着进入下一个概念粒,直至最终全部完成。

在标记使用上,IGL算法与以往所有基于标记等价的算法不同的是:IGL算法的预设标记和代表标记完全无关。预设标记可无序;代表标记连续递增。为约束预设标记的赋值范围,减少计算量,给出以下定理。

推论标记任意一个N×M图像的过程中,临时连通区不超过sup(N/2)个。

同理可知,以上定理、推论可用于N×N或任意区域(此时N是区域的最大宽、高度)。以图1所示概念粒为例演示IGL的提取和标记过程。

图1 概念粒示例

令图1所示的概念粒号为6。首行第6行成为当前行,R(6,2,25)被赋预设标号1,R(6,32,45)为2,分别记作TC61和TC62,更新W={1,2}。第7行,R(7,3,5),R(7,19,23)和R(6,2,25)连通,被依次并入TC61。TC62完毕,记作连通粒C61,W={1}。第8行,R(8,2,5),R(8,16,25)被顺序并入TC61,R(8,7,12)得到预设标号2,记为新的TC62,W={1, 2}。第9行,R(9,2,5),R(9,17,26)被顺序并入TC61,R(9,8,13)则并入TC62。R(9,33,42)得预设标号3,记作TC63,W={1,2,3}。第10行,R(10,2, 5),R(10,15,26)被顺序并入TC61,R(10,34,43)并入TC63。TC62完毕,记作C62,W={1,3}。第11行,R(11,6,17),R(11,20,40)被顺序并入TC61。在R(11,20,40)并入TC63时,被发现已得到正标号1,不等于3,即TC63应和TC61合并。合并过程:将R(9, 33,42)置于R(9,17,26)之后,R(10,34,43)置于R(10,15,26)之后,R(11,20,40)置于R(11,6,17)之后。至此,本概念粒最后一行毕,记TC61为C63。即图1中有3个连通粒:C61～C63。

以上标记、提取及相关的统计操作在图像的一次扫描中完成,优于当前的基于等价标记的标记算法。

IGL算法旨在为后续处理提供基础平台,所得连通粒除了有标记之外,在标记过程中已将每个连

通区单独以压缩方式存放,并附有区域大小、边缘特征等统计信息,平台的应用者可以随机独立地访问其中的任何一个,也可轻松地根据需要为连通粒建立索引。

3.3 算法实现

以式(5)做依据,定义针对行连通段的结构体类型run:

typedef struct run;

接下来的标记和提取的实现有2个关键步骤。

(1)临时连通区的指针组的定义与使用。设N是图像的宽度,或是不规则(例如是图1所示的概念粒)区域的最大宽度,Tn=sup(N/2)+1,按照推论定义指针组:run∗TC［n+1］［Tn］;n为概念粒号。

(2)连通和合并的判定。为简化实现算法的说明,设y代表当前行,y1是它的下一行,R(y,s,t)为当前行的当前行连通段,R(y1,s1,t1)为下一行中待检测的行连通段,根据6设计连通、合并的判定算法如下。

算法连通与合并判定算法

4 验证与对比分析

为测试IGL算法对资源有限环境的适应性,本文用低配置设备做了验证比较实验,用的是一台笔记本电脑(Intel(R)Pentium(R)T2330@1.60 GHz, 1 GB内存,MPSoC),VC60和OpenCV 2编程。

测试图像集共有220幅自然图像(包括指纹图、风景图、肖像等,引自贝克利分割库),另有20幅纹理图(引自哥伦比亚反射纹理库),10幅Canny边缘图,和25幅医学图像(引自芝加哥大学医学图像库)。

4.1 彩色图像的验证与分析

彩图标注是个热点,有众多成果,彩图标记则尚未见诸公开文献,没有同类可比较的文献,是种探索。为验证IGL算法提供的基础平台的应用潜力,从连通粒与图像中潜在对象的对应性及标记速度2个角度给出实验结果,验证基础平台的应用潜力。

在表1中,Ci列为每幅图经截分后得到的概念粒之一,作为示例,CCj列出该概念粒中的一个连通粒,Nc是全图概念粒总数,Ncc为全图连通粒总数。

表1彩图的粒标记验证示例

对比CCj列中的连通粒和Ci列对应对象,所有10个实例中,两者都有严格的、精确的对应性,同时也基本反映出了原图像中对应的潜在对象的原貌,为依据连通粒分析对应对象打下了扎实的基础。

图2显示了10幅图像(按序与表1对应)的运行时间及连通粒总数(Ncc)。为了直观,后者显示连通粒总数除以35 000的值。从结果看,运行时间均在1%秒级,比较快捷,能适应低资源环境。整体趋势上,运行时间随着连通粒的增加而提高,但也有局部震荡(如road1)。分析具体数据,发现这是受了图像本身的连通结构影响,road1的平均行连通长度偏短。

图2 运行时间与连通粒数

为了进一步分析连通粒数对运行速度的影响,用最高值与最低值之比粗略地估计两者的增速。根据表1、图2,连通粒数最少的为tower2.jpg,256个,对应的运行时间为0.031 s。最多的是mushr.jpg, 159 3个,运行时间是0.078 s。即在连通粒总数增加6.22倍的情况下,时间的增幅是2.52倍。特别的,在极端情况下,在连通粒总数高达22 217个(tower2的87倍)时,运行时间也仅为0.352 s (tower2的11倍)。这从一个侧面说明,限制预设标记数对因连通粒增加而带来的图像复杂性有抑制作用,提升了处理速度,因此,IGL算法能较好地适应复杂图或大图的快速标记。

实验证实IGL算法找到的区域与图像中的潜在对象有较好的对应性,作为有着严密的理论依托的基础平台,它可在图像处理和分析领域中的众多研究方向上得到应用,比如图像检索、显著对象提取、图像语义标注等。

4.2 对比分析

RTS算法是目前较突出的灰度图基于行连通段标记算法之一,且已被文献［13］证实快于其他标记算法,因此本文选择与文献［13］提出的RTS算法作比较分析。

表2列出了有代表性的8种类型共15幅二值图像的实验结果。表中CC列显示实际的连通粒数,RTS列记录RTS算法的预设标记数,IGL是相应的IGL算法的预设标记数,结果数据显示,两者最少相差7倍,最大时,近于70倍,IGL算法所用的预设标记远低于RTS算法。

表2 所用标识数比较

用表2中所有图像做标记所用时间比较,见图3,表中每个时间值为运行1 000次总时间的平均值,实验结果显示出IGL算法在所有被测图像上都快于RTS算法。

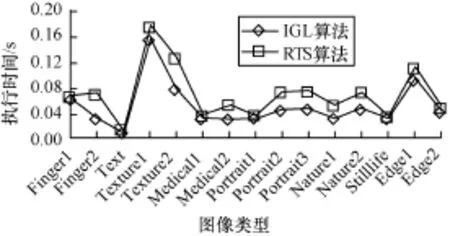
图3 不同类型图的运行时间

这种速度差异有着客观原因:(1)如表2所示,IGL算法的预设标记远低于RTS算法,且其上限可预知。(2)在RTS算法中,由预设标记中产生代表标记,也就是说,预设标记将被代表标记划分成一个个集合,表2显示,一个图中的连通区数量通常较大,数目也不定,这些集合的记录存储将很费时,相对的,在IGL算法中,预设标记与代表标记无关,不必记录。(3)RTS搜索需合并的临时连通区时,用的仍是逐象元方式,IGL算法则完全基于行连通段。

5 结束语

本文构建并实现了一个图像粒标记模型,并给出了相应的实现算法——IGL算法,形成了一种可同时适应灰度图和彩图的基础标记平台。平台有严格的粒计算理论基础,可扩展性强,速度快,所得连通粒信息全,与图像中的潜在对象有对应性,能用于诸如显著对象局部提取、图像检索、图像语义标注等众多图像分析方向。

［1]张 钹,张 铃.粒计算未来发展方向探讨［J］.重庆邮电大学学报:自然科学版,2010,22(5):538-540.

［2]马鸿耀,王国胤,张清华,等.基于云模型的多粒度彩色图像分割［J］.计算机工程,2012,38(20): 184-187.

［3]姚 红,王国胤,张清华.基于粗糙集和云模型的彩色图像分割方法［J］.小型微型计算机系统,2013, 34(11):2615-2620.

［4]Milind M M,Ray A K.Color Image Segmentation: Rough-set Theoretic Approach［J］.Pattern Recognition Letters,2008,29(4):483-493.

［5]任小康,李文静,靳艳峰.基于粗糙集和mPCA的人脸识别算法［J］.计算机工程,2008,34(14):178-181.

［6]Petrosino A,Ferone A.Rough Fuzzy Set-based Image Compression［J］.FuzzySetsandSystems,2009, 160(10):1485-1506.

［7]谢 昭,高 隽.一种基于粗糙集区域分割和语义分类的方法［J］.模式识别与人工智能,2007,20(2): 287-294.

［8]Yao J T,Vasilakos,A V,Pedrycz W.Granular Computing:PerspectivesandChallenges［J］.IEEE Transactions on Cybernetics,2013,43(6):1977-1989.

［9]王国胤,张清华.不同知识粒度下粗糙集的不确定性研究［J］.计算机学报,2008,31(9):1588-1598.

［10]李仲生,李仁发,蔡则苏.显著对象的非监督粗糙认知算法［J］.计算机研究与发展,2012,49(1):202-209.

［11]李仲生,李仁发,蔡则苏,等.稀疏表示下的非监督显著对象提取［J］.电子学报,2012,40(6):1097-1102.

［12]李仲生,蔡则苏,黄同成,等.粒边缘模型及其实现［J］.计算机工程与应用,2014,50(5):1-5.

［13]He L,Chao Y,SuzukiK.A Run-basedTwo-scan Labeling Algorithm［J］.IEEE Transactions on Image Processing,2008,17(5):749-756.

编辑 顾逸斐

An Image Granule Labeling Model and Its Implementation

LI Zhongsheng1,HUANG Tongcheng1,CAI Zesu2
(1.Department of Information Engineering,Shaoyang University,Shaoyang 422000,China;
2.School of Computer Science and Technology,Harbin Institute of Technology,Harbin 150001,China)

With regard to the absence of base models which are extendible in the field of image analysis,an image granule labeling model is proposed.On the analysis of the applicability of rough sets and quotient space,two new concepts,semantic granule and conception granule,are defined and the image labeling model based on granules is constructed with them.A linear algorithm,Image Granule Labeling(IGL)algorithm,is presented for the realization of the granule labeling model with the definitions of connected segment in a line and potential connection range between two lines.It simplifies connectivity determination using a dynamic set of provisional labels and takes into account the fact that the quantity of granules may be huge and the structure of granules is very complex normally.Comparisons and experimental results on binary images and color images show that the proposed granule labeling algorithm is effective and accurate,and it is quicker than conventional labeling algorithms.

connected segment in a line;connected granule;conception granule;image processing;granule labeling model;Image Granule Labeling(IGL)algorithm

李仲生,黄同成,蔡则苏.一种图像粒标记模型及其实现［J］.计算机工程,2015,41(3):223-227,236.

英文引用格式:Li Zhongsheng,Huang Tongcheng,Cai Zesu.An Image Granule Labeling Model and Its Implementation［J］.Computer Engineering,2015,41(3):223-227,236.

1000-3428(2015)03-0223-05

:A

:TP391.41

10.3969/j.issn.1000-3428.2015.03.042

国家自然科学基金资助项目(61075076);湖南省自然科学基金资助项目(13JJ6078,14JJ7075);湖南省教育厅基金资助重点项目(13A091)。

李仲生(1967-),男,副教授、博士,主研方向:图像处理,粒计算,物联网技术;黄同成,教授、博士;蔡则苏,副教授、博士。

2014-01-28

:2014-05-12E-mail:zsli666@163.com