应用于分布式存储系统的准循环再生码构造方案
李晨卉
(复旦大学上海市智能信息处理重点实验室,上海200433)
应用于分布式存储系统的准循环再生码构造方案
李晨卉
(复旦大学上海市智能信息处理重点实验室,上海200433)
传统纠错码编码方案能够提高系统容错能力,但在数据修复时会占用大量带宽。为此,基于循环结构,构造一种面向分布式存储系统的准循环最小存储再生码。根据该准循环再生码的冗余系数向量权重和修复带宽边界,设计一种改进的节点修复算法,证明其修复带宽在最好情况能达到最小割下界,在最坏情况下也优于最大距离可分码的修复带宽。实验结果表明,该再码构造方案不仅节省存储空间,而且具有构造简单、运算代价低和修复带宽小等特点。
网络编码;分布式存储系统;准循环;再生码;最小存储再生码;数据修复
1 概述
随着数字信息从文本到多媒体的转变以及社会信息化进程的加快,信息量开始呈几何级数爆炸性地增长,海量数据的存储和处理受到社会各界越来越广泛的关注。如今,海量数据存储已成为一个备受瞩目的研究热点。分布式存储系统(Distributed Storage System,DSS)是一种结合了互联网和存储技术的、面向海量数据的存储解决方案。然而,由于网络不稳定,分布式存储系统中很容易发生因节点失效导致数据无法取回的情况,因此通常需要采取某种冗余机制来提高可靠性。同时,系统需要具有对失效节点所存储的数据进行修复的能力以维持其容错性能,但这一过程可能会造成大量数据传输。
复制是最简单并常见的冗余方案,通过保存2个或2个以上原数据的副本,保证某处硬盘故障或网络中断不影响该部分数据的取用,然而这种方案消耗太多额外存储空间。相比之下,传统的纠删码方案在很大程度上提高了数据的存储效率(在保证系统容错等级的同时减少了冗余占用的额外存储空间),其中最著名的一类纠错码称为最大距离可分(Maximum Distance Separable,MDS)码,但这种编
码策略在数据修复时会产生很大的带宽消耗和计算负载。
针对该问题,文献[1]将网络编码技术与分布式存储码技术相结合,提出一种新型再生码编码方案。利用网络编码技术,再生码策略能够在保证系统容错性能(与MDS码具有相同的容错性能)的同时,优化数据修复过程的带宽消耗。然而,网络编码技术是一种使网络中的中继节点具有编码能力以达到信息论中多播网络的理论最大流界的通信领域新概念,以此为基础改进的再生码在数据修复时通常具有复杂的节点内运算,以及为达到低修复带宽而增加的存储消耗。为此,本文提出一种适用于分布式存储系统的新型准循环再生码构造方案。
2 数据修复与再生码
在介绍数据修复以及再生码前,以最具代表性之一的MDS码为例,介绍纠错码编码策略。假设原数据大小为B,编码基域为有限域Fq(q是有限域的大小),分布式存储系统一共有n个节点。一个[n,k]MDS码的基本思想是:将大小为B的数据分成k个数据分组,并编码为n个分组的数据(n>k,且每个新分组的大小与原分组相等),其中,任意k个分组都可完整恢复原数据,该过程称为数据重建。这种编码系统可以容忍n-k个分组丢失,如图1所示。

图1 纠错码原理
本文称这种由任意k个分组完整重建原数据的性质为MDS性质。当存储节点失效后,MDS码的节点修复策略是先连接有效节点中的任意k个节点,进行数据重建,然后再根据编码规则重新生成失效节点的数据。这种方案为修复一个大小为B/k的数据分组同时传输大小为B的数据量,传输带宽消耗远大于节点存储的数据量,尤其是在节点分布较分散的DSS中,节点修复所消耗的额外网络带宽更加明显。
根据节点修复的定义,无需大量数据传输就能实现节点修复。如图2所示,原数据被分成4块,分别用A1,A2,B1,B2表示,并编码为一个[4,2]MDS码,每个节点存储2块数据。节点2先线性运算B1⊕B2,然后再上传给数据收集器(Data Collector, DC),同时连接节点1、节点3分别下载A1,A2+B2,在新节点通过一定线性运算完成数据修复。这样修复过程只需消耗3块数据大小的带宽,而且实现了节点的精确修复。其实,节点修复只定义修复得到的新节点加入后系统仍满足MDS性质,因此新节点可以是不同于原失效节点的数据分组的线性组合。基于该定义,得到另外2种数据修复模型:功能性修复和系统部分精确修复。
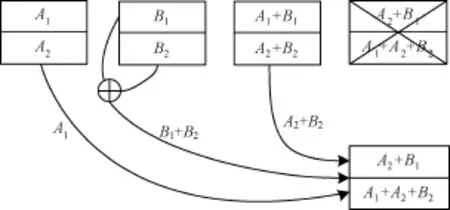
图2 精确修复[4,2]MDS码的节点4
精确修复是指修复操作所生成的新节点存储的数据与原失效节点完全一致。功能性修复[1]要求低一些,只需修复操作所生成的新节点加入后系统依然保持MDS性质,因此新节点存储的数据可以与原失效节点不同。系统部分精确修复是指对于失效节点存储的系统码(即未编码的数据分块)部分采取精确修复原则,而非系统码部分依照功能性修复原则。
在功能性修复模型下,文献[2]通过采用修复过程的信息流图建模得到的修复带宽能够达到理论上的最小割下界,利用图2中的[4,2]MDS码为例展示这一过程,如图3所示。虚拟源节点S代表原数据B=4,将每个存储节点表示成一对节点并通过一条有权边相连,边的权值就是该节点的存储容量α=2。将DC作为虚拟汇节点,并使它连接任意k=2个节点,d表示连接的节点数,b表示修复时从每个连接节点传输的数据量。

图3 功能性修复[4,2]MDS码的信息流
图3显示了节点X4(虚线椭圆部分)失效时,系统重新构建一个与其具有相同存储结构的节点X5来替代它的过程。根据最大流最小割定理[3],最小割值必须大于等于S发送的数据量,DC才能重建原数据。显然,图3中的最小割为α+2β=B=4(虚线表
示),意味着βmin=l,修复带宽γmin=dβ=3。根据信息流图的最小割分析,参数必须满足以下条件才能构成再生码[4]:

显然,当α和β达到最小值时就会得到修复过程的最低资源消耗。不过由于α和β无法同时达到最小,因此在B,k,d确定时,可以得到当α取最小得到最小存储方案或β取最小得到最小带宽方案的一个折衷曲线,称取得该曲线上点的α和β时对应的编码方案为再生码,并从中得到2个极值情况:最小存储再生(Minimum Storage Regeneration,MSR)码和最小带宽再生(Minimum Bandwidth Regenerating, MBR)码。其中,MSR码满足以下性质:
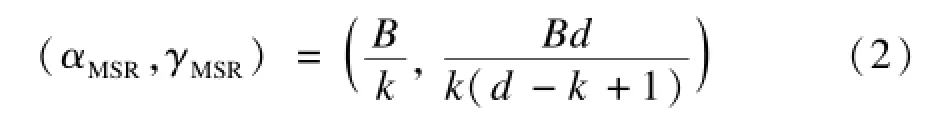
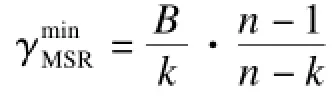
MBR码满足以下性质:
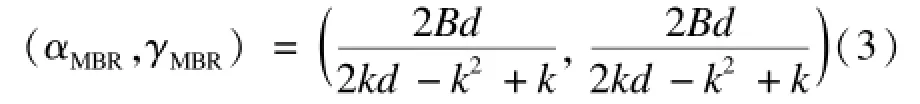

功能性修复虽然对系统修复操作的要求更低,修复实现的难度更小,但存在3点不足:(1)节点修复后需要更新系统的数据重建和修复算法;(2)功能性修复的实现需要很大的有限域来满足动态增大的有向无环图,导致编解码的计算复杂度较高;(3)动态的修复和解码过程容易发生信息泄露,因此安全性较差。所以,功能性修复具有局限性。
精确修复不仅没有功能性修复带来的上述缺陷,而且还能够保证进行节点修复后系统内始终保存一份完整的系统码,这样用户读取数据时系统无需运算就可以快速并行地传输全部原数据,这使得精确修复成为当前的首选策略。通过干扰对齐技术,可以找出可精确修复的MSR码[4-5],并推导出以下2个定理。
定理1(Exact-MSR码) 假设MDS码率[6]不大于1/2,即(k/n)≤1/2,并且d≥2k-1,那么通过干扰对齐可以达到式(2)所示的MSR码边界。同时,修复机制是可确定的,并且需要的有限域不大于2(n-k)。
定理2 在不使用符号扩展且b=1的情况下,达到割集边界的线性精确修复MSR码在d<2k-3时不存在[7]。
3 应用于分布式系统的准循环再生码构造
准循环再生码是一种基于循环结构的线性编码,构造简单,且通过预定义的节点修复系数向量和修复算法大大降低了修复产生的运算代价。
假设在一个[n,k,d]再生码中,原信息被分隔成B个数据块,并编码成n个节点,其中,每个节点包含α个分块。DC可以通过任意k个节点完整恢复出原数据。对于一个失效节点,新节点能通过连接任意d个可用节点并从每个节点下载β个分块重建该节点,节点修复所消耗的带宽称为修复带宽,用γ表示,且有γ=dβ。
3.1 准循环再生码的定义
在准循环再生码中,定义α=2,即每个存储节点包含2个分块,并规定每个节点的第1个分块存储原数据(即系统码),第2个分块存储冗余码(用于数据修复和可靠性保护)。由此可知,在准循环再生码中,有B=n。由于准循环再生码也是一种线性网络编码,因此其第2个分块的冗余数据均为系统码的线性组合,并且其冗余系数向量满足循环结构。
用G表示一个[n,k,d]准循环再生码的编码矩阵,则G满足如下公式:


存储系统能够并行地提取数据且不需要译码。除非特殊声明,本文中。
定义如果一个[n,k,d]存储码的编码向量c=[c1|c2]满足以下2个性质,则称其为准循环再生码:
(2)节点修复性质:假如节点n失效,存在一组{i1,i2,…,id}∈{1,2,…,n-1},使能够通过[h1,h2,…,hd]计算得到,其中,hj(1≤j≤d)是c1,ij和c2,ij的线性组合。
3.2 准循环再生码的构造
应用于分布式存储系统的准循环再生码的构造过程如图4所示,用S={1,2,…,n}代表存储节点的集合,用向量υ=(υ1,υ2,…,υn)表示n个分块的系统码,用向量ρ=(ρ1,ρ2,…,ρn)表示相应的n个冗余码,称ρ为冗余向量。

图4 准循环再生码的构造过程
由式(4)准循环码的构造矩阵可知,节点中第2块存储的冗余码与行向量c2,i相关,又由于c2具有循环结构,定义c2如式(5)所示:

其中,λt∈GF(p),t=1,2,…,n,λn+i=λi=λi-n;c2,i为冗余系数向量,同时可以用ωt(c)表示c2,i的权重,因为有ωt(c2,1)=ωt(c2,2)=…=ωt(c2,n)。
根据式(6)定义冗余向量ρ:

编码矩阵G可以表示为:

显然,G是一个n×2n的矩阵,可以简单地将G的第n+i列移到第i列右边(1≤i≤n)构建一个新的编码矩阵G^:其中,G^与G共轭,G用于表示分布式存储系统的存储结构,而G^用于后文对其性质的推导。

4 准循环再生码的性质及节点修复
4.1 准循环再生码的性质分析
令s={i1,i2,…,ik}∈S,且|s|=k。将矩阵G^的列序号表示成以下形式:{2×1-1,2×1,…,2i-1, 2i,…,2n-1,2n},假设M[s]是一个任取G^中k组2i-1列和2i(i∈s)列构造的矩阵。
命题在一个[n,k,d]准循环再生码中,如果满足式(9),任意k个节点都能完整恢复原数据:


定理3 设Q(x1,x2,…,xn)∈F[x1,x2,…,xn]是一个多元多项式[8],总度数为d0(总度数是加和表达式中所有项的最大度数,其中一个项的度是指变量的幂指数)。对有限集合S∈F,从中随机选取n个互不相同的数r1,r2,…,rn,如果Q(x1,x2,…,xn)不为0,则:
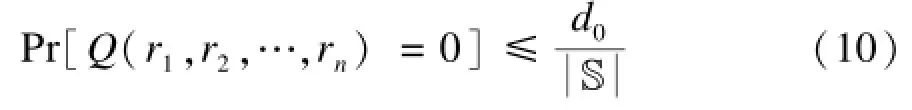
通过命题和定理3可以得到以下推论:

定理4 如果存在[n,k,d]准循环再生码,其冗余系数向量c2,i=[λn-i+2,λn-i+3,…,λn,λ1,λ2,…,λn-i+1]且λ1≠0,则存在相应的[n,k,d]准循环再生码,且有冗余向量c′2,i=[λn-i+2,λn-i+3,…,λn,0,λ2,…,λn-i+1]。
证明:不失一般性地,假设节点n失效。对任意的[n,k,d]准循环再生码,且其冗余系数向量c2,i为上述准循环结构,令λ1=0得到相应的c′2,i。对一个由c′2,i构造的[n’=n,k’=k,d’=d]存储码,只需证明它是一个准循环再生码,就可证明定理成立。
(1)数据重建性质的符合性验证
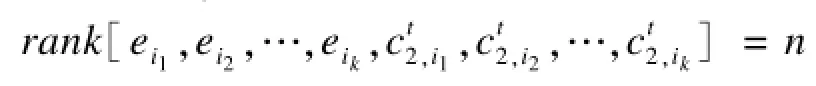
因为[n,k,d]存储码是一个准循环再生码,根据数据重建性质,有:
其中,i1,i2,…,ik∈{1,2,…,n}。值得注意的是,在c2,ij(j∈{1,2,…,k})修改后(令λ1=0),矩阵的秩并没有改变,即:

这说明[n’,k’,d’]存储码满足数据重建性质。
(2)节点修复性质的符合性验证
在一个[n,k,d]准循环再生码的节点修复过程中,可以不失一般性地假设存储节点n失效,则编码向量[en,c2,n]能够通过下列公式修复:
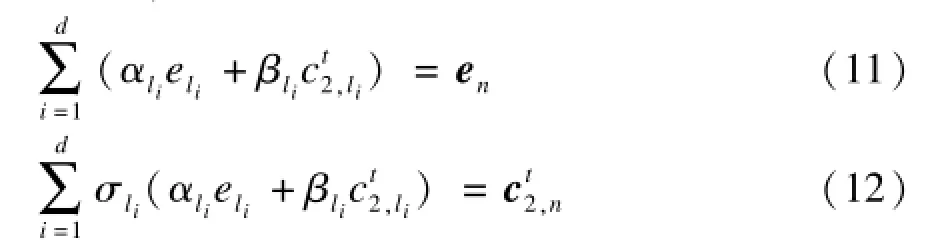
其中,l1,l2,…,ld∈{1,2,…,n-1};ρli,αli,βli∈GF(p),i∈{1,2,…,d}。根据式(11)可以得到:
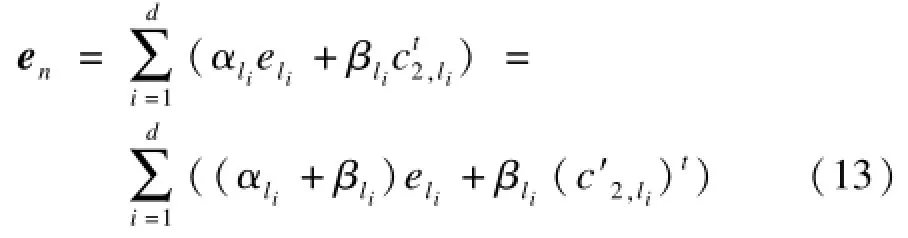
根据式(12)可以得到:

根据式(13)、式(14)可以得出,[n′,k′,d′]存储码满足节点修复性质,因此由[n,k,d]推导出的[n′,k′,d′]存储码是准循环可再生码,且ωt(c′)=ωt(c)+1。
4.2 数据修复与算法分析
根据定理4得知,如果存在λ1≠0的准循环再生码,则可以推出相应λ1=0的准循环再生码。在研究性质的过程中,均假设λ1=0。
假设λ1=0且λn=0,则编码矩阵G为:

文献[9-10]提出一种弹性的准循环MSR (Quasi-cyclic Flexible MSR,QCFMSR)码,它的构造与本文构造类似,只是在参数设置和定义上做了更严格的限定,是本文所描述的准循环再生码的一种特例。令β=1,i∈{2,3,…,k+1}时,λi≠0;i∈{1,k+2,k+3,…,n}时,λi=0;得到QCFMSR码。文献[10]给出一种节点修复算法,这种算法通过一定的扩展可以用于本文所定义的编码结构,但其修复带宽较大,为n-1,且仅能容忍1个节点失效。
下文将讨论本文所定义的准循环再生码在节点修复方面的性质,并给出改进的节点修复算法。
定理5对一个[n,k,d]准循环再生码,如果有α=2,β=1,则:



为保持数据重建性质,从任意k个节点传输的编码系数向量必须线性独立,所以有:
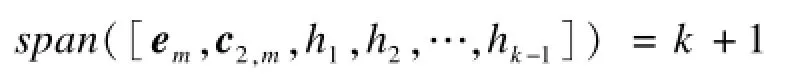
因此,可以得到:
定理6对一个[n,k,d]准循环再生码,冗余系数向量的权重ωt(c)满足:


(1)因为ρm=λn-m+2υ1+λn-m+3υ2+…+λ2n-m+1υn,用{1,2,…,n}标记c2,m=[λn-m+2,λn-m+3,…,λ2n-m+1]中各项的位置坐标,选其中不为0的项的坐标{l1,l2,…,lw},其中,w≤n,则ωt(c)=w。同时,ρm可以通过坐标对应的系统码集{υl1,υl2,…,υlw}的线性组合计算得到。
(2)在除了节点m外的其他节点中找到一个c2,k,它坐标位m上项的值不为0。类似步骤(1),取节点c2,k中所有不为0的项对应的系统码集(节点m除外)v={υk1,υk2,…,υkw-1},如果其还未被连接,则连接该节点并下载其第一分块,则υm能够通过v= {υk1,υk2,…,υkw-1}和c2,k的线性运算得到,其中, |v|=ωt(c)-1。
通过以上步骤,能够修复节点m。过程中消耗的带宽为γ≤ωt(c)+(ωt(c)-1)+1=2ωt(c)。根
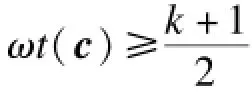
推论2 对一个[n,k,d]准循环再生码,冗余系数向量的权重ωt(c)满足:

下文给出一种节点修复算法,该算法不仅可以精确修复失效节点,而且能保证在最好情况下修复带宽达到最小割下界。如果令i∈{k+1,k+2,…,n}时,λi≠ 0;且i∈{1,2,…,k}时,λi=0;当k为奇数时,采用修复算法可以达到修复带宽的下界k+1。
算法当λ1=0且λn=0时的准循环再生码修复算法
输入编码矩阵和失效节点标号i
输出节点i存储的2块数据
(1)在c2,i中找到所有值非零的项,根据标记坐标{1,2,…,n}对应得到非零项的坐标集{l1,l2,…,lw},并连接S中相应位置的节点,下载其第一分块,根据冗余系数向量c2,i可以通过线性运算得到节点i的第二分块。
(2)在所有c2,i,j≠i中找到一个其位置i的值非零的冗余系数向量c2,j,寻找方法是将c2,i反置,从节点i+1处为起始位一一对应,第1个非零位对应的节点即所求节点。然后,下载节点j的第二分块,并对节点j进行与第(1)步类似的操作,取节点c2,j中所有不为0的项对应的系统码集(节点m除外)v= {υj1,υj2,…,υjw-1},如果对应的节点未被连接,则连接该节点并下载其第一分块,则vj能够通过v={υj1,υj2,…,υjw-1}和c2,j的线性运算得到。
算法的第(1)步传输的数据带宽为w=ωt(c),第(2)步传输的数据带宽为|v|+1≤(ωt(c)-1)+ 1=ωt(c)。因此一次修复过程消耗的带宽为γ≤2ωt(c)。
推论3 对一个[n,k,d]准循环再生码,使用修复算法进行节点修复时,修复带宽γ满足:k+1≤γ≤n-1。
根据该修复性质,可以给出一种准循环MSR (QCMSR)码的构造方法,使α=2,β=1,令ϑ={j1,j2,…,jk}⊆{2,3,…,n},其中,j1,j2,…,jk是连续的自然数,且j∈J时,λi≠0;j∈{2,3,…,n}ϑ时,λi= 0;得到QCMSR码,具有以下性质:
(1)当d=k+1时,根据MSR码满足的条件,即式(2),有α=d-k+1,从而得到d=k+1;
(2)当B=n=2k时,根据式(2)有B=k(d-k+ 1),将性质(1)代入等式即可得到。
下面给出一个采用修复算法进行节点修复并达到带宽最小割下界的示例,一个[6,3,4]QCMSR码,冗余系数向量c2,1=(0,0,0,1,1,1),根据循环结构可以得到其他节点的冗余系数向量,假设第2个节点S2失效,则修复过程如图5所示。

图5 算法对[6,3,4]QCMSR码失效节点S2的修复情况
在图5中,用1和2表示修复步骤(1)、步骤(2),点线箭头指明了反置后的冗余系数向量c2,2=(1,0,0,0,1,1)的第1个非零位所匹配到的节点,计算过程如修复算法所述。可以看出,步骤(1)、步骤(2)共消耗的带宽为γ=k+1=4,参与修复的节点只进行数据传输,然后在新节点通过2次线性运算最终完成对节点的精确修复。修复算法具有“传递并修复”的性质,即节点中不需要对其2个分块进行线性运算,运算复杂性较低。
5 结束语
本文将网络编码技术应用于分布式存储系统的编码方案中,利用中间节点编码优化修复过程的带宽消耗。在研究再生码及不同数据模型,并与传统纠错码的性能进行比较后,提出一种适用于分布式存储系统的新型准循环再生码编码方案,阐述了其定义和构造方法,并对其构造条件和性质进行分析和证明。同时,针对该编码方案的节点修复性质进行分析,给出一种改进的节点修复算法,并证明算法修复带宽在最好情况能够达到最小割下界,在最坏情况下也优于MDS码,并通过对参数的设置给出一种准循环MSR码构造方案,不仅存储消耗小而且能够达到修复带宽的最小割下界。
在接下来的工作中将进一步优化该修复算法,以及讨论在α>2的情况下第2个分块为循环结构的准循环结构再生码的性质。因为修复算法在一些情况下并不是最优化的修复策略,即修复一个节点所消耗的带宽并不一定达到最小带宽,所以可以针对算法继续进行优化,使得当编码结构中每个节点的第2个分块都用循环结构时,修复带宽尽可能为最小[11]。此外,本文只讨论了α=2下的情况,未讨
论此参数推广到更大范围的情况。现有研究结果表明[12-13],当α=3且k≥4时,使每个节点的第2个分块用循环结构的构造方式不存在精确修复。对于α推广到更大范围时准循环再生码的节点修复还没有相关结论,是下一步需要深入研究的问题。
[1]Dimakis A G,Ramchandran K,Wu Y,et al.A Survey onNetworkCodesforDistributedStorage[J].Proceedings of the IEEE,2011,99(3):476-489.
[2]Dimakis A G,Godfrey P G,Wu Y,et al.Network Coding for Distributed Storage Systems[J].IEEE Transactions on Information Theory,2010,56(9): 4539-4551.
[3]卢开澄,卢华明.图论及其应用[M].北京:清华大学出版社,2005.
[4]Wu Y,DimakisA G,RamchandranK.Deterministic Regenerating Codes for Distributed Storage[C]//Proceedings of the 45th Annual Allenton Conference on Communication,Control,and Computing.Washington D.C., USA:IEEE Press,2007:2276-2280.
[5]Wu Y,Dimakis A G.Reducing Repair Traffic for Erasure Coding-based Storage via Interference Alignment[C]// Proceedings of IEEE International Symposium on Information Theory.Washington D.C.,USA:IEEE Press,2009: 2267-2280.
[6]Suh C,Ramchandran K.Exact Regeneration Codes for DistributedStorageRepairUsingInterferenceAlignment[C]//Proceedings of IEEE International Symposium on Information Theory Proceedings.Washington D.C., USA:IEEE Press,2010.
[7]Shah N B,Rashmi K V,Kumar P V,et al.Interference Alignment in Regenerating Codes for Distributed Storage: Necessity and Code Constructions[J].IEEE Transactions on Information Theory,2012,58(4):2134-2158.
[8]Yeung R W,Li Y R,Cai N,et al.Network Coding Theory[M].Boston,USA:Now Publishers Inc.,2006.
[9]Gaston B,Pujol J,Villanueva M.Quasi-cyclic Minimum StorageRegeneratingCodesforDistributedData Compression[C]//Proceedings of Data Compression Conference.Washington D.C.,USA:IEEE Press,2011: 33-42.
[10]Gaston B,Pujol J,Villanueva M.Quasi-cyclic Flexible Regenerating Codes[EB/OL].(2012-12-13).http:// arxiv.org/licenses/nonexclusive-distrib/1.0/.
[11]Kan Haibin,Shen Hong.Lower Bounds of the Minimal Delays of Complex Orthogonal Designs with Maximal Rates[J].IEEE Transactions on Communications,2006, 54(3):383-388.
[12]Kan Haibin,Shen Hong.A Relation Between the Characteristic Generators of a Linear Code and Its Dual[J].IEEE Transactions on Information Theory,2005,51(3): 1199-1202.
[13]Yuan C,Kan Haibin.A Characterization of Solvability for a Kind of Networks[J].Science China Information Sciences,2012,55(4):747-754.
编辑 陆燕菲
Construction Scheme of Quasi-cyclic Regenerating Code for Distributed Storage System
LI Chenhui
(Shanghai Key Laboratory of Intelligent Information Processing,Fudan University,Shanghai 200433,China)
Traditional erasure coding scheme is universally adopted to enhance the fault tolerance,which produces too much data transmission in a repair process.A new construction scheme of quasi-cyclic Minimum Storage Regenerating (MSR)regenerating codes is proposed in this paper.According to its property of exact repair about the weight of encoding vector and the bound of repair bandwidth,it proposes an improved node repairing algorithm which optimizes the repair bandwidth to the cut-set bound,and it is also better than Maximum Distance Separable(MDS)codes in the worst case.Experimental result shows that the construction scheme not only can save the storage space but also has simple structure,low operation cost and low repair bandwidth,etc.
network coding;Distributed Storage System(DSS);quasi-cyclic;regenerating code;Minimum Storage Regenerating(MSR)code;data recovery
李晨卉.应用于分布式存储系统的准循环再生码构造方案[J].计算机工程,2015,41(3):81-87.
英文引用格式:Li Chenhui.Construction Scheme of Quasi-cyclic Regenerating Code for Distributed Storage System[J].Computer Engineering,2015,41(3):81-87.
1000-3428(2015)03-0081-07
A
TP393
10.3969/j.issn.1000-3428.2015.03.015
上海市科委基础研究基金资助重点项目(12JC1401400)。
李晨卉(1989-),女,硕士研究生,主研方向:网络编码,信息安全,密码学。
2014-04-18
:2014-05-16E-mail:chenhuili11@fudan.edu.cn

