山岭隧道涌水量预测方法分类及相关因素分析

顾博渊， 史宝童， 黄　嫚

(中交第一公路勘察设计研究院有限公司， 陕西 西安　710075)



山岭隧道涌水量预测方法分类及相关因素分析

顾博渊， 史宝童， 黄嫚

(中交第一公路勘察设计研究院有限公司， 陕西 西安710075)

摘要：准确预测隧道涌水量能有效减少隧道病害，保护生态环境，科学指导隧道的设计与施工，而如何正确选择和应用预测方法，是准确预测的前提条件。通过广泛调研，在总结分析各类涌水量预测方法的原理和适用范围基础上，以六盘山隧道某断面为例，深入探讨了围岩渗透系数、洞室尺寸、地下水位净高变化、注浆圈厚度、注浆水平和衬砌抗渗等级等因素对隧道涌水量的影响，重点指出各类解析方法的局限性和适用条件，突出了注浆水平在实际工程中的作用，并建议山岭公路隧道衬砌抗渗等级不宜小于S8。

关键词：隧道涌水量； 地下水动力学； 注浆； 抗渗等级； 预测方法

0引言

涌水量是隧道动态设计信息化施工的关键参数，同时也是隧道修建对区域环境影响评价的关键因素之一。目前,我国已建、在建的隧道均存在不同程度的涌水和渗漏水问题。鉴于隧道地下水问题的重要性，国内外学者对隧道地下水涌水量问题进行了大量研究。王晓明等[1]采用降水入渗法，结合蒙特卡洛随机模拟技术，对河北省水峪隧道的涌水量进行概率研究，为隧道涌水量预测提供了一种概率分析方法；陈冬等[2]试用SWMM模型，模拟以管道为主的岩溶隧洞涌水过程，分析SWMM模型对岩溶隧道涌水量动态变化模拟的适用性；王建宇[3]从地下水的渗流作用出发对作用于隧道衬砌的水压力荷载的计算进行了讨论，着重指出了不同水头高度情况下水压力的折减方法和排导系统的设置方式；喻成云[4]通过收集隧道实际涌突水样本数量，从数学统计的角度分析隧道涌突水量的主要影响因素，并从统计角度建立了回归方程；肖智兴等[5]使用遗传算法优化BP神经网络的初始权值和阈值，建立了水下隧道涌水量的遗传-神经网络预测模型，并进行了计算分析。从调研的成果不难发现，很多学者针对某一种涌水量预测方法研究的比较深入、透彻，但缺少预测方法之间横向、定量的比较，本文在归纳总结常用涌水量预测方法的基础上，重点针对影响隧道涌水量的几个主要因素进行分类讨论，详细分析了相同水文地质条件下不同预测方法的变化规律，希望为实际应用中涌水量预测方法的选择和有效预测提供借鉴和参考。

1隧道涌水量预测方法对比分析

1.1隧道涌水量预测方法简介

我国自20世纪80年代起，随着技术水平和施工要求的提高，开始对隧道涌水量的预测进行系统的研究，尤其是在90年代取得了长足的进步，从定性分析逐步转变为定量评价与计算，而随着计算技术的不断发展和渗流理论的不断完善，提出了很多新的隧道涌水量计算方法，归纳起来主要有2大类，即确定性数学模型方法和随机性数学模型分析方法[6-9]。前者主要包括比拟法、径流模数法、解析法等，后者主要包括灰色关联度法、时间序列分析及频谱分析法等，详细分类及应用条件如表1所示。

表1　隧道涌水量计算方法分类

1.2各种预测方法适用范围

水均衡法原理简单明了，但预测结果偏差较大，适用于工程可行性研究阶段宏观概略地预测隧道涌水量；若初测、定测阶段已逐步开展了相应的地勘工作，气象水文地质资料详尽，可采用地下水动力学法、降雨入渗法和水文地质比拟法预测隧道涌水量；数值计算法建立在正确的水文地质模型基础上，是目前解决复杂条件下水文地质问题的有效方法，其计算精度主要取决于模型参数的准确性，特别适用于运营期隧道排水量的预测。

从隧道埋深、地层岩性等角度考虑，浅埋隧道适合采用降雨入渗法和水文地质比拟法；深埋隧道适合采用地下水动力学法和数值计算方法；泥岩、砂岩等均质围岩地区适合采用水文地质比拟法和地下水动力学法；岩溶区隧道或地下水系发育的地区适合采用随机性数学模型分析方法和地下径流模数法等方法综合预测。

2地下水动力学法预测隧道涌水量影响因素分析

2.1地下水动力学法预测隧道最大涌水量

隧道涌水量预测通常包括正常涌水量预测和最大涌水量预测。正常涌水量是指隧道的涌水达到大致稳定时的涌水量，最大涌水量是指隧道在含水体中掘进时的峰值涌水量。预测隧道涌水量是隧道工程建设的重要内容之一，而地下水动力学法理论成熟，原理简单，推导方便，相对于随机性数学模型分析方法或数值计算方法，现场勘察和计算工作量较少，便于应用，是宏观研究山岭公路隧道涌水量控制的有效方法之一，也是高速公路隧道工程地质勘察中最常用的方法。其简化模型如图1所示。

隧道最大涌水量常用计算公式有以下几种[10-13]：

1) Goodman(1965)

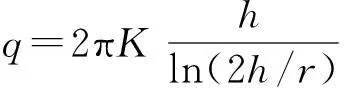
(1)

h—隧道中心到地下水位线的距离；r—隧道半径；pa—大气压力水头，一般pa=0； d—地表水深度，若无地表水，则d=0。

图1计算模型简图

Fig. 1Computation model diagram

2)karlsrud (2001)

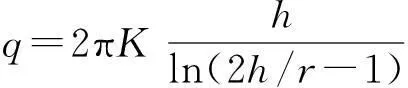
(2)

3)Lei(1999)

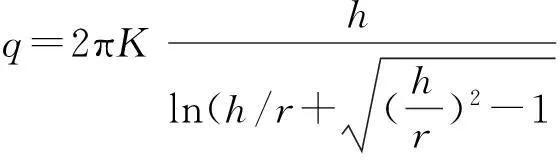
(3)

4)Lombardi(2002)

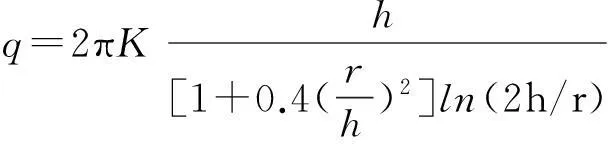
(4)

5)均质解析解

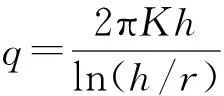
(5)

6)EI Tani(2003)

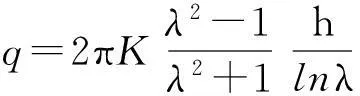
(6)

7)佐藤邦明

(7)

式中：m为换算系数，一般取0.86；hc为含水层厚度。

8)大岛洋志公式

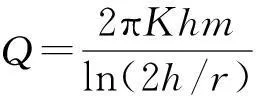
(8)

比较式(1)和式(8)可知，大岛洋志预测隧道涌水量的公式增加了一个经验修正系数m(m=0.86)，以综合考虑实际工程水文地质边界条件的复杂性和不确定性。

9)朱大力公式

TB 10049—2004《铁路工程水文地质勘察规程》根据工程实例总结出预测隧道最大涌水量的经验公式

q0=0.025 5+1.922 4 K×H。

(9)

式中H为含水层中原始静水位到隧道底板的距离。

上述预测隧道最大涌水量公式可概括为3个类型，经典解析解，式(1)—(6)；半理论半经验公式，式(7)和(8)；纯经验公式，式(9)。式(1)—(8)公式组成结构类似，推导原理相似，均可概括为

q0=2πmKh·f(h,r)。

(10)

式中f(h,r)为h、r的函数[14]，表达式不同，取值不同，可理解为原静止地下水位的折减系数。

2.2隧道最大涌水量影响因素比较分析

从式(10)可以看出，地下水动力学解析解预测隧道涌水量的因素主要有围岩渗透系数、地下静止水位高度和洞室尺寸3种，为比较分析这3种因素在预测隧道涌水量中的作用和变化规律，以六盘山隧道某断面为例，等效圆半径为5.85 m，渗透系数3.20×10-7m/s，隧道埋深为200 m，计算若无特殊说明上述参数均保持定值不变。

2.2.1围岩渗透系数

围岩渗透系数是隧道涌水量预测的重要参数，施工现场一般通过地质钻孔抽水试验获取。在地下水位高度、洞室尺寸不变的情况下，隧道涌水量随围岩渗透系数变化曲线如图2所示。从图2可以看出朱大力经验公式预测值最大，地下水动力学经典理论解析解预测值居中，其中，除均质解析解预测值稍大外，其他解析解预测值基本相同；大岛洋志公式在Goodman公式的基础上考虑了经验系数m=0.86，实则是对Goodman公式的折减；佐藤邦明公式除了考虑经验系数m，还考虑了含水层厚度的影响，预测值最小。

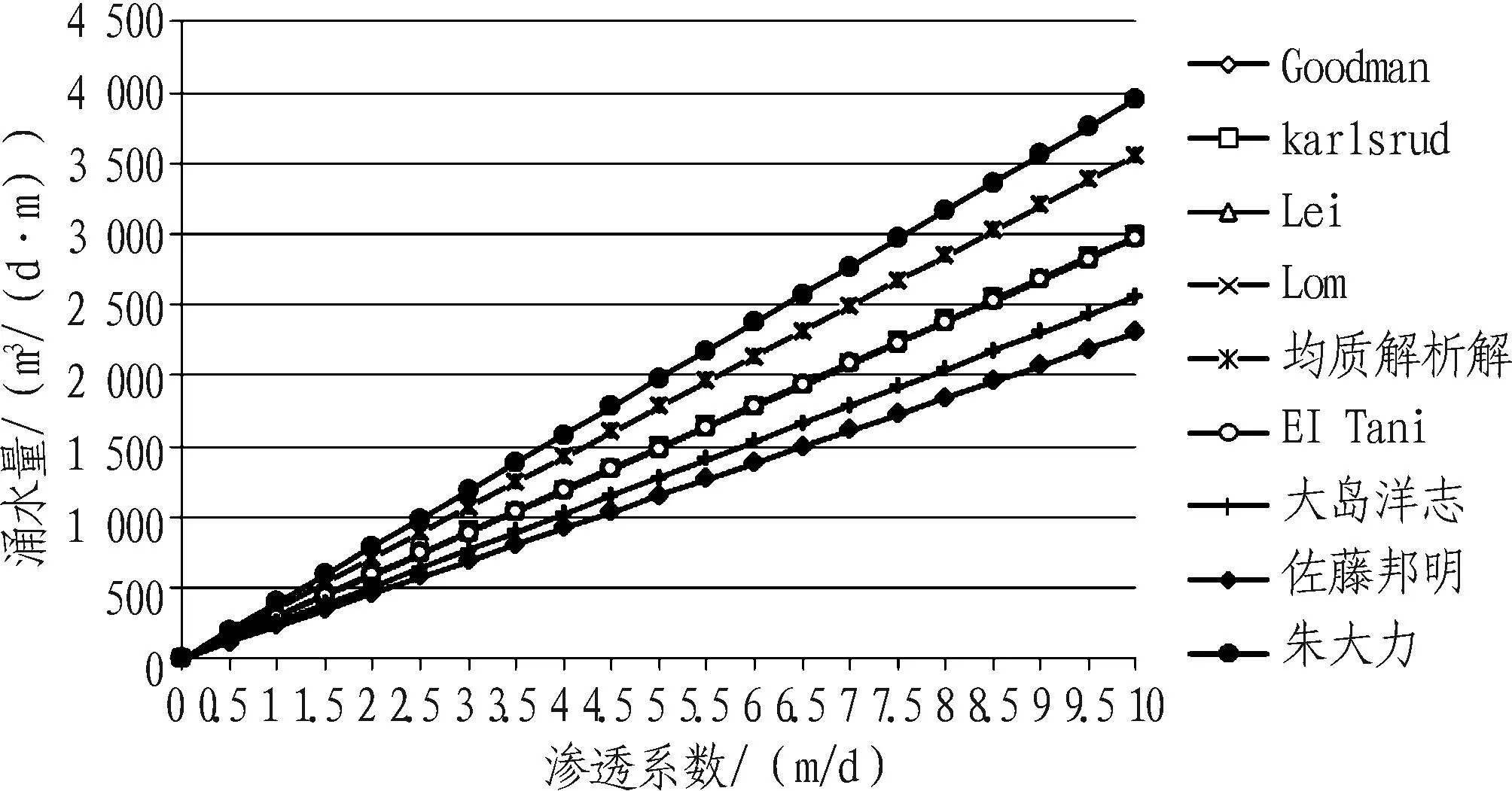
图2　涌水量随渗透系数变化曲线

2.2.2洞室尺寸

在围岩渗透系数和地下水位高度不变的情况下，隧道涌水量随洞室尺寸变化情况如图3所示。除朱大力公式外，其他公式预测隧道涌水量随洞室尺寸增大而增大，变化趋势基本相同，当隧道洞径小于5 m时，变化曲率较大，大于5 m时，变化趋势逐渐平缓。朱大力公式预测值基本不随洞径尺寸变化，这与该公式的计算参数有较大关系，仅在H(原始静水位到隧道底板的距离)中考虑了洞室尺寸效应，因一般情况下隧道半径远小于H，故其预测值随洞室尺寸变化不明显，且在洞径尺寸较小时，预测值明显偏大。

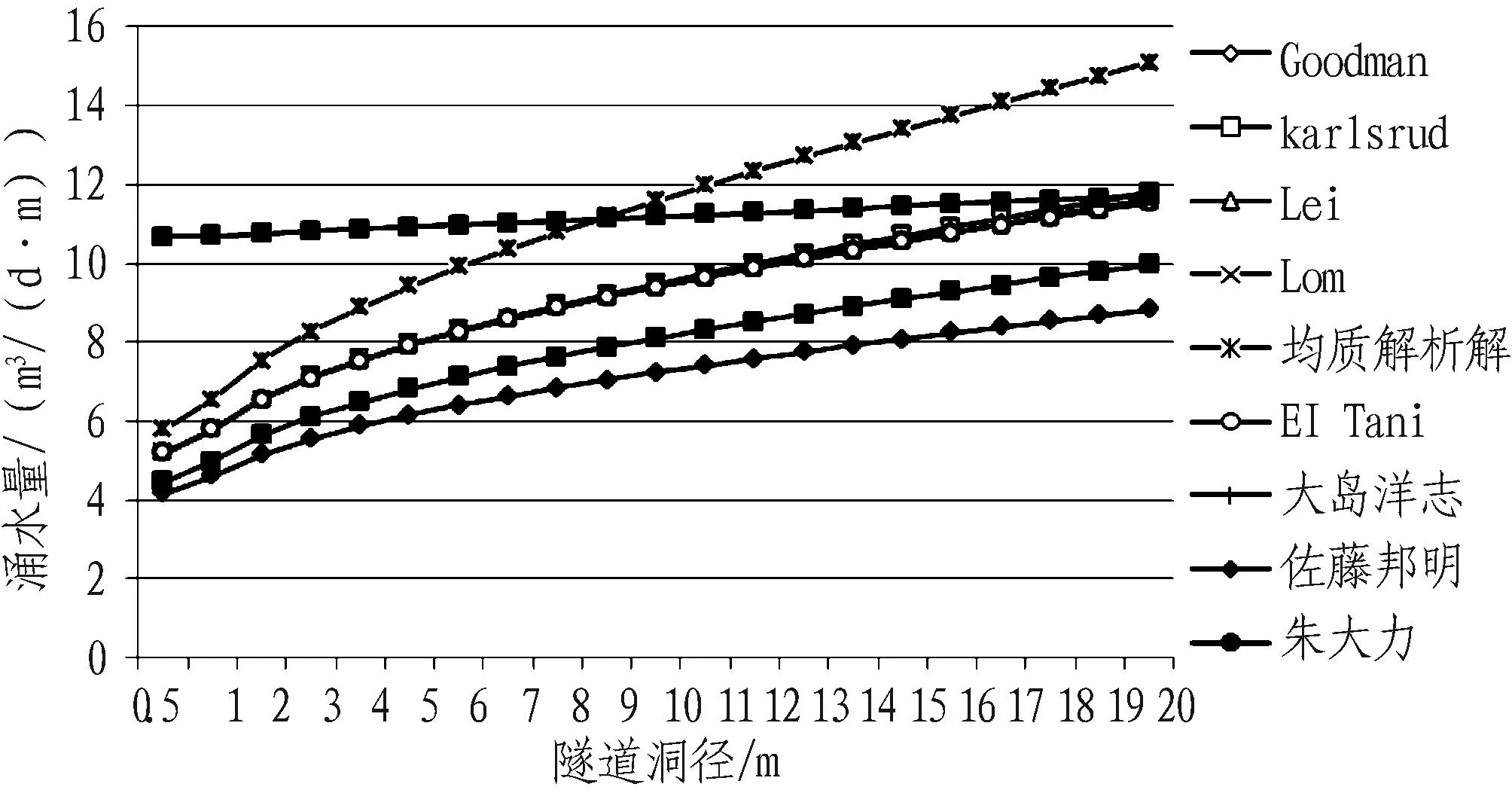
图3　涌水量随洞室尺寸变化曲线

除经验公式外，同一洞径尺寸各公式预测隧道涌水量大小关系与图2所示规律基本一致，均质解析解预测值最大，佐藤邦明最小。

2.2.3地下水位净高变化

地下水位净高是指地下稳定水位面到隧道中心的距离，在围岩渗透系数和洞室尺寸不变的情况下，隧道涌水量随地下水位净高变化曲线如图4所示。从图4可以看出，隧道涌水量随地下水位的增加出现一个先减小后增大的过程，即存在一特定水位净高，可使隧道涌水量最小，按本例计算参数，这一水位净高约为10 m。在地下水位净高较小时，均质解析解预测值偏大，其他理论解析解居中，随着水位的不断增加，均质解析解预测值与经验公式预测值拟合度较高，其他理论解析解和半理论半经验解析解预测值偏小。

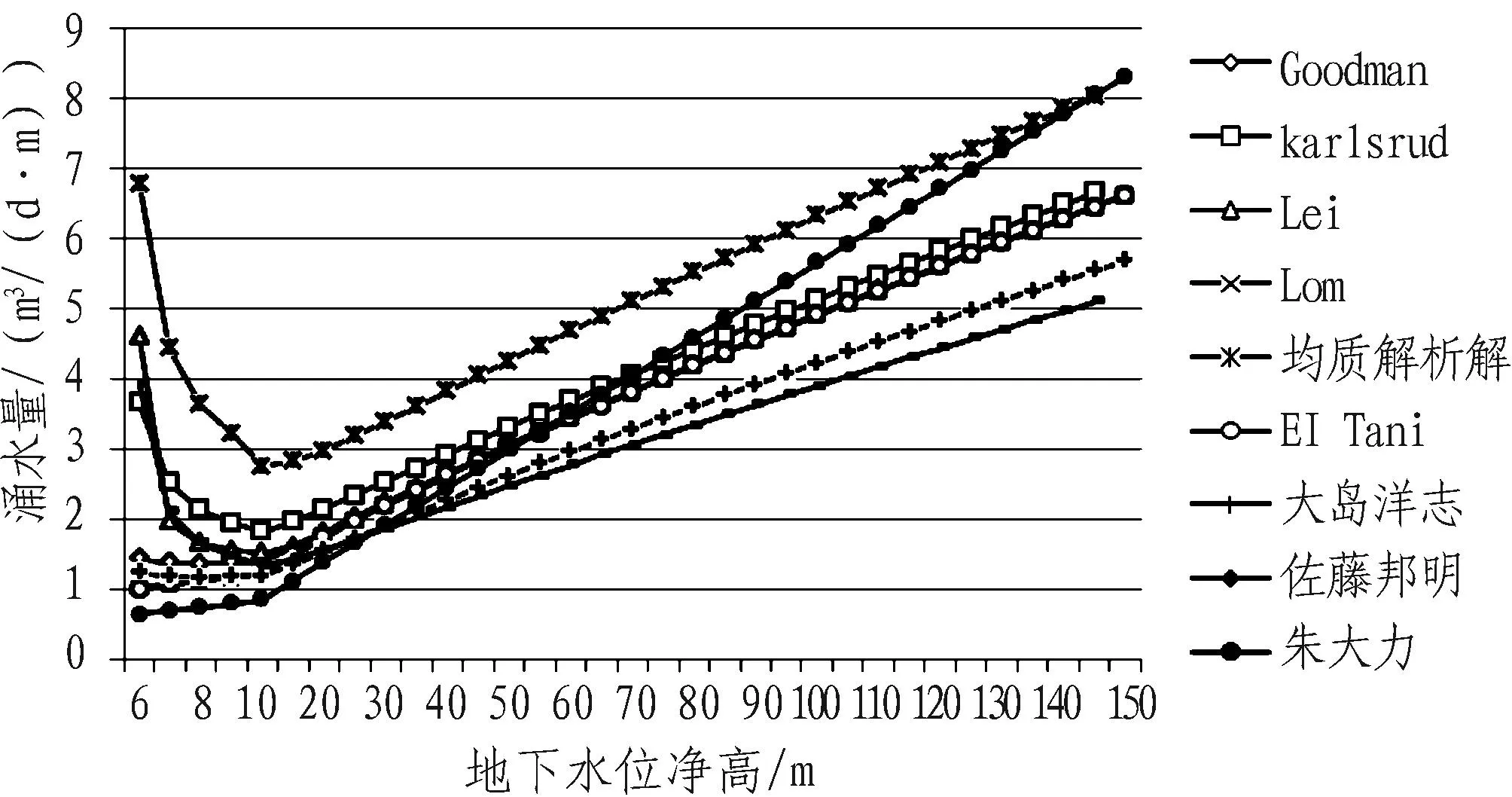
图4　涌水量随地下水位高度变化曲线

综合以上隧道涌水量预测与各因素的变化规律，经典理论解析解(Goodman、karlsrud、Lei、Lom、EI Tanis)适用于地下水位净高较小时涌水量预测，当水位净高较大时预测结果偏小；均质解析解适用于高水位隧道涌水量预测，当水位较低时预测结果偏大；在应用朱大力经验公式时，应注意洞室尺寸规模，当尺寸较小时预测结果偏大；半理论半经验公式(大岛洋志、佐藤邦明)折减系数m=0.86，预测结果相对偏小，可做为上述方法的对比和补充。

3洞周注浆技术及衬砌抗渗等级对隧道涌水量的影响

除地层岩性、地质构造及地下水位等地理地质因素外，隧道施工本身，如施工方案、衬砌参数等也会对隧道涌水量的大小产生影响，其中，洞周注浆技术及衬砌抗渗性能是影响最显著的因素，高水位地区多采用增设注浆圈的方法来降低衬砌外水压力，控制地下排水量；而衬砌抗渗等级的选择更显“随意”性，缺少必要的设计依据，本节主要针对隧道施工过程中该2种因素对隧道涌水量的影响展开论述。

3.1洞周注浆技术对隧道涌水量的影响

一般而言，作用在隧道上的水荷载是渗流产生的体积力，需要通过对实际地层进行渗流场分析才能确定作用在衬砌上的水荷载以及隧道的排水量。假定围岩为均质各向同性连续介质，王秀英等[15]提出了一种新型隧道涌水量计算方法，假设隧道为圆形，地下水头很高，设为H，水流为稳定流，其运动规律服从达西定律。r0为衬砌内径；r1为衬砌外径；rg为注浆圈半径；r2为远场距离，等于H，计算简图如图5所示。

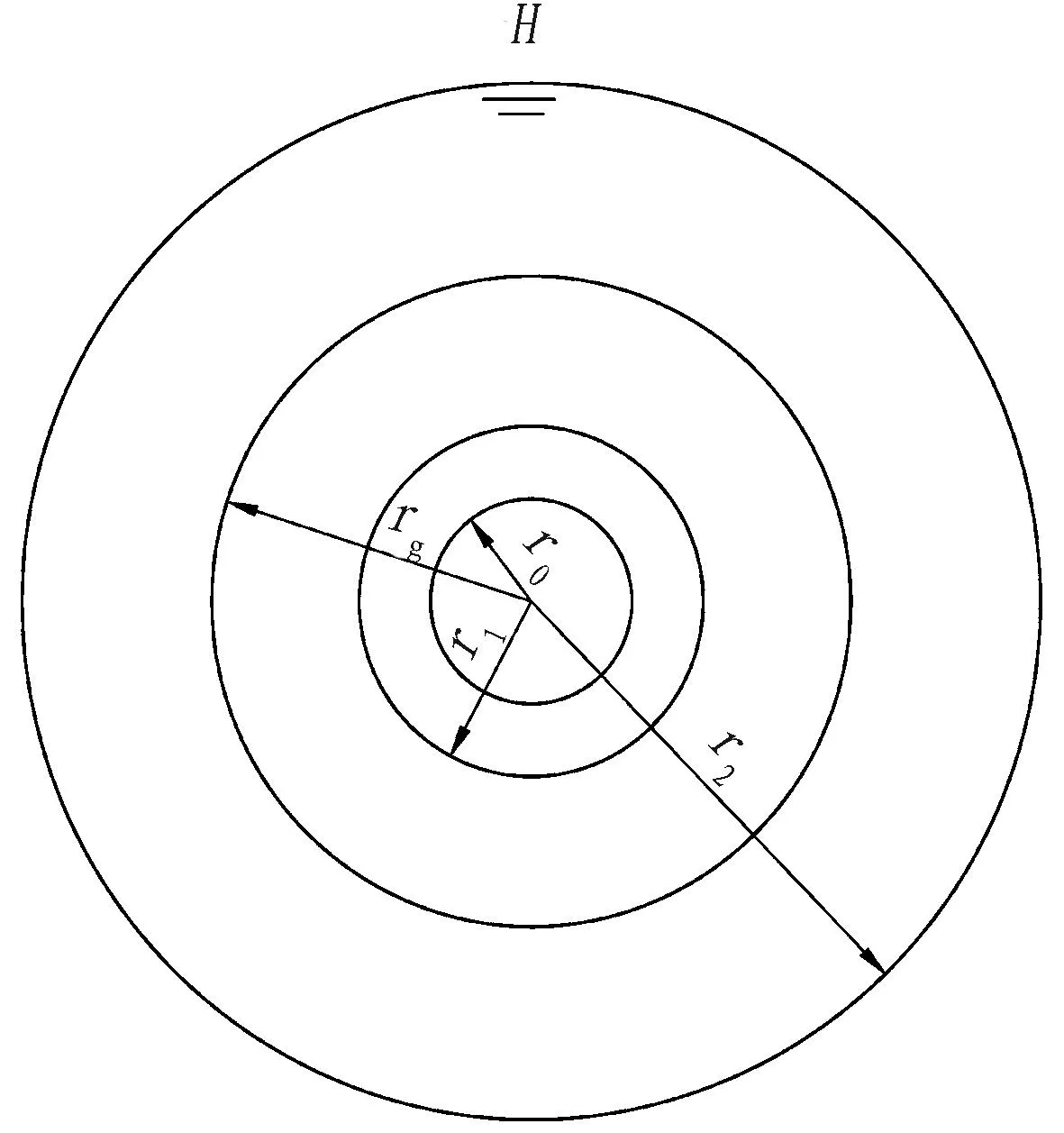
图5　隧道涌水量计算简化模型

根据渗流连续性方程(即Laplace方程)，可推导得出未注浆情况下每延米隧道涌水量

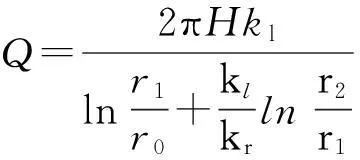
(11)

有注浆止水帷幕的情况下每延米隧道涌水量

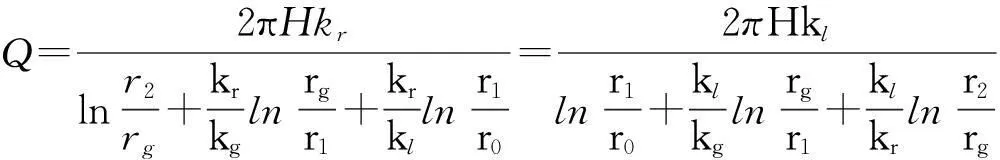
(12)

式中：kl为衬砌渗透系数；kg为注浆体渗透系数；kr为围岩渗透系数。

由上述公式可知，隧道涌水量不仅与注浆圈厚度密切相关，还与围岩和注浆圈渗透系数的比值、地下水位高度等条件有关。现以六盘山隧道最高水位断面为例，应用式(12)分析围岩注浆条件下隧道涌水量的变化规律。

1)不同注浆圈厚度与隧道涌水量的关系如图6所示，隧道涌水量随着注浆圈厚度的增大而逐渐减小，在相同注浆效果情况下，当注浆圈厚度≤10 m时，隧道涌水量随注浆圈厚度的增加明显减小，当注浆圈厚度>10 m时减小趋势变缓，说明注浆水平和注浆圈厚度均存在一个经济合理的范围，不能盲目地通过增加注浆圈厚度来减少隧道涌水量。

图6　注浆圈厚度与隧道涌水量的关系

2)注浆效果与隧道涌水量的关系如图7所示，在相同注浆圈厚度Lq的条件下，随着kr/kg的增大(即注浆效果的提高)，隧道排水量逐渐降低。若设定隧道涌水量小于5 m3/(d·m)，当注浆圈厚度为3 m时，kr/kg需大于200；当注浆圈厚度为5 m时，kr/kg需大于115；当注浆圈厚度为7 m时，kr/kg需大于85。注浆圈厚度越小，要求注浆圈的渗透系数越小，即注浆效果更好，而相对于增加注浆圈厚度，进一步提高注浆水平来控制隧道涌水量更合理、经济。

图7　注浆水平(kr/kg)与隧道涌水量的关系

3.2衬砌抗渗等级对隧道涌水量的影响

衬砌结构是隧道防排水体系中的重要一环，同时兼顾承载、安全和防水的目的，其施工质量和抗渗性能直接关系到后期隧道运营安全。目前，山区高速公路隧道设计中衬砌抗渗等级多采用S6，部分项目采用S8，主要依据隧址区地下水位高度和围岩渗透性能来定，本节通过数值计算方法建立了隧道涌水量与衬砌抗渗等级的关系曲线，如图8所示，表2为各抗渗等级混凝土对应的渗透系数。

图8　隧道涌水量与衬砌渗透系数的关系曲线

Table 2Impermeability grade and permeability coefficient of tunnel lining

渗透等级渗流系数/(cm/s)隧道渗流量/(m3/(d·m))S10.32×10-73.219S20.16×10-71.095S40.66×10-80.554S60.34×10-80.234S80.21×10-80.077S100.14×10-80.056S120.10×10-80.041

由图8可以看出，随着衬砌抗渗等级的提高，隧道涌水量逐步减少，当衬砌抗渗等级由S1提高到S8时，隧道的涌水量显著减少，减小量达97.61%；而当抗渗等级由S8提高到S10、S12时，减小量分别为0.66%、1.1%，抗渗等级超过S8之后，隧道涌水量减小程度明显变缓，逐渐趋于平稳，综合目前我国施工技术水平及环境保护的需求，建议山岭公路隧道衬砌抗渗等级不宜小于S8，同时在混凝土凝胶材料中可掺入CMA抗裂剂等掺料25～30 kg/m3，以进一步提高衬砌的自防水能力和结构的耐久性。

4结论与体会

1)预测隧道最大涌水量的方法可概括为以下3个类型： 地下水动力学经典理论解析解、半理论半经验公式和纯经验公式。经典理论解析解适用于地下水位净高较小时涌水量预测；纯经验公式不能考虑洞室尺寸的效应，断面较小时预测结果偏大；半理论半经验公式存在折减系数，预测结果相对偏小。

2)隧道涌水量随着注浆圈厚度的增大及注浆水平的提高逐步减小，注浆水平和注浆圈厚度均存在一个经济合理的范围，不能盲目地通过增加注浆圈厚度来减少隧道涌水量，而相对于增加注浆圈厚度，进一步提高注浆水平来控制隧道涌水量更合理、经济。

3)建议山岭公路隧道衬砌抗渗等级不宜小于S8，同时在混凝土凝胶材料中可掺入CMA抗裂剂，进一步提高衬砌抗渗性、抗裂性和耐久性。

由于山岭隧道地下水运动规律复杂，涌水量预测应根据项目具体的工程地质条件、地形地貌特征和水文边界条件有针对性地选择，目前较为常用的是确定性数学模型方法，随机性方法涉及因素多，计算复杂，一般做为确定性方法的补充和验证。但各种预测方法就实际应用情况来看，预测精度还远远不够，特别是针对运营期隧道排水量的预测还有待进一步研究。

参考文献(References)：

[1]王晓明，曹正波.基于水均衡方法的隧道涌水量概率预测[J].交通标准化,2014, 42(23): 112-114,118.(WANG Xiaoming,CAO Zhengbo. Probabilistic prediction of water inflow into a tunnel using water balance method[J]. Transportation Standardization,2014, 42(23): 112-114,118.(in Chinese))

[2]陈冬，许模，曾科，等. SWMM模型模拟岩溶隧道涌水量的动态变化过程分析： 以中坝隧道为例[J].地下水,2014, 36(1): 82-84.(CHEN Dong,XU Mo,ZENG Ke,et al. SWMM model to simulate the dynamic process analysis of karst tunnel water inflow[J].Ground Water，2014,36(1): 82-84.(in Chinese))

[3]王建宇.对隧道衬砌水压力荷载的讨论[J].现代隧道技术,2006(增刊)： 67-73.(WAGN Jianyu.The discussion about water pressure load on the tunnel lining [J]. Modern Tunnelling Technology, 2006(S): 67-73.(in Chinese))

[4]喻成云.基于统计分析的西南岩溶区隧道涌水量预测探析[D].成都: 成都理工大学,2013.(YU Chengyun. Based on statistical analysis of southwest China karst tunnel inflow forecast analysis[D]. Chengdu: Chengdu University of Technology, 2013.(in Chinese))

[5]肖智兴,黄涛,李政,等. 遗传-神经网络算法在水下隧道涌水量预测中的应用[J].水资源与水工程学报,2011, 22(3): 102-105.(XIAO Zhixing,HUANG Tao,LI Zheng,et al. Application of genetic-neural network algorithm to forecast water inflow in underwater tunnel [J]. Journal of Water Resources & Water Engineering, 2011, 22(3): 102-105.(in Chinese))

[6]田海涛,董益华,王延辉.隧道涌水量预测的研究[J].水利与建筑工程学报,2007, 5(3): 75-77,97.(TIAN Haitao,DONG Yihua,WANG Yanhui. Study on forecasting for water-gushed yield of tunnel[J]. Journal of Water Resources and Architectural Engineering, 2007, 5(3): 75-77,97.(in Chinese))

[7]姜爱民,杨辉,张明.确定性数学模型方法预测隧道涌水量研究[J].工程勘察,2012,40(6): 37-41.(JIANG Aimin,YANG Hui,ZHANG Ming. Study on deterministic mathematical model for predicting water gushing yield of tunnel [J]. Geotechnical Investigation & Surveying, 2012, 40(6): 37-41.(in Chinese))

[8]陶玉敬,彭金田,陶炳勋.隧道涌水量预测方法及其分析[J].四川建筑,2007, 27(6): 109-113.(TAO Yujing,PENG Jintian,TAO Bingxun. Tunnel water inflow forecasting methods and analysis. [J]. Sichuan Architecture,2007, 27(6): 109-113.(in Chinese))

[9]郑黎明.隧道涌水灾害预测的随机性数学模型方法[J].西南交通大学学报,1998,33(3): 273-278.(ZHENG Liming. A stochastic mathematic method for predicting gushing water from tunnel surrounding rockmasses [J]. Journal of Southwest Jiaotong University,1998,33(3): 273-278.(in Chinese))

[10]Karlsrud K.Water control when tunneling under areas in the Oslo region[J].NFF Publication,2001,12(4): 4-27.

[11]LEI Shizhong.An analytical solution for steady flow into a tunnel[J].Ground Water,1999,37(1): 23-26.

[12]李鹏飞,张顶立,周烨.隧道涌水量的预测方法及影响因素研究[J].北京交通大学学报,2010,34(4): 11-15.(LI Pengfei,ZHANG Dingli,ZHOU Ye.Study on prediction methods and its influence factors of water inflow into tunnels[J]. Journal of Beijing Jiaotong Universety,2010,34(4): 11-15.(in Chinese))

[13]王建秀,朱合华,叶为民.隧道涌水量的预测及其工程应用[J].岩石力学与工程学报，2004,23(7): 1150-1153.(WANG Jianxiu,ZHU Hehua,YE Weimin. Forward and inverse analyses of water flow into tunnels[J].Chinese Journal of Rock Mechanics and Engineering，2004,23(7): 1150-1153.(in Chinese))

[14]袁广祥,杨莉,李刚.解析法预测隧道可能最大涌水量的对比研究[J].华北水利水电学院学报,2013,34(6): 12-15.(YUAN Guangxiang,YANG Li,LI Gang. Contrastive research on analytical methods to predict probable maximum water yield into tunnel [J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power,2013,34(6): 12-15.(in Chinese))

[15]王秀英,王梦恕,张弥.计算隧道排水量及衬砌外水压力的一种简化方法[J].北方交通大学学报, 2004,28(1): 8-10.(WANG Xiuying,WANG Mengshu,ZHANG Mi. A simple method to calculate tunnel discharge and external water pressure on lining[J].Journal of Northern Jiaotong Universety, 2004,28(1): 8-10.(in Chinese))

Classification of Water Inflow Prediction Methods for

Mountain-crossing Tunnels and Analysis on Related Factors

GU Boyuan, SHI Baotong, HUANG Man

(CCCCFirstHighwayConsultantsCo.,Ltd.,Xi’an710075,Shaanxi,China)

Abstract:The accurate prediction of the tunnel water inflow is helpful in minimizing the tunnel disease, protecting the environment and guiding the design and construction of the tunnel. However, the selection of proper water inflow prediction method, as well as its proper application, is a prerequisite for the accurate prediction of the water inflow. In the paper, the principles and application scopes of various water inflow prediction methods are summarized and analyzed, and the influence of the surrounding rock permeability coefficient, tunnel dimension, groundwater level, grouting ring thickness, grouting effect and lining impermeability grade on the water inflow is analyzed, with Liupanshan tunnel as an example. Furthermore, the limitations and application scopes of the analytical methods are provided, the application of the grouting effect in the water inflow prediction is highlighted, and it is proposed that the impermeability grade of the lining of mountain-crossing highway tunnels should not be inferior to S8.

Keywords:tunnel water inflow; groundwater dynamics; grouting; impermeability grade；prediction methods

中图分类号：U 45

文献标志码：A

文章编号：1672-741X(2015)12-1258-06

DOI:10.3973/j.issn.1672-741X.2015.12.004

作者简介：第一 顾博渊(1981—)，男，上海崇明人，2003年毕业于同济大学，隧道及地下工程专业，硕士，高级工程师，现从事高速公路隧道设计工作。

收稿日期：2015-03-30; 修回日期: 2015-05-13