考虑双重竞争的供应链系统定价策略研究

李 扬，曲铁平，李慧玲

(1.沈阳理工大学 理学院，辽宁 沈阳 110159；2.沈阳市第一私立高中，辽宁 沈阳 110043)

考虑双重竞争的供应链系统定价策略研究

李 扬1，曲铁平1，李慧玲2

(1.沈阳理工大学 理学院，辽宁 沈阳 110159；2.沈阳市第一私立高中，辽宁 沈阳 110043)

在由一个制造商和两个零售商组成的闭环供应链中，考虑两个零售商之间对同质产品的销售竞争和回收竞争，分别将制造商和两个零售商作为两个系统，研究这两个集中式供应链的系统最优定价策略，及定价受回收竞争系数的影响。结果表明，两个系统的销售价均与回收竞争系数负相关，而回收价均与回收竞争系数正相关。

供应链；双重竞争；定价策略

环境保护是我国政府一直重视的问题，近些年由于科技进步，回收的旧产品也可以经重新制造后如同新产品一样卖给消费者。这样做不但环保，而且制造商也有利润可图，因为用旧产品重新制造的费用往往都小于用原材料加工的费用。现代市场中回收并重新制造的例子很多，比如美国施乐公司、惠普公司等。既然回收并重新制造可多获利，那零售商之间销售竞争和回收竞争就自然会同时存在。本文主要考虑销售与回收双重竞争下供应链系统的定价策略问题。

研究闭环供应链成员竞争与定价策略的文献很多，Kannan Govindan等[1]涵盖了从2007年1月至2013年3月国际发表的382篇高水平文章，并从多方面进行了详细的分类总结。Liang等[2]给出了一种对重新制造产品的定价选择方法。Savaskan等[3]提出了对于废旧产品回收不同渠道结构选择问题，并考虑了不同回收渠道中零售商的竞争对渠道成员所做决策的影响。不同于单渠道问题，文献[4-5]研究了多个回收渠道下闭环供应链的定价及决策问题，丰富了闭环供应链的回收渠道形式。

以上研究都集中在供应链定价策略上，并没有讨论是否可达到供应链的完美协调。Dekker等[6]定性分析了闭环供应链协调问题的关键，并讨论了价格决策的协调问题。Shantanu Bhattacharya等[7]研究了一个零售商向制造商订购新产品和向再制造商订购再造品的最优订购数量问题，采用收益共享机制可使供应链达到完美协调。

以上文献主要针对确定性需求的问题，有关需求不确定的文献也有很多，比如Shi等[8]和OnurKaya[9]研究了需求不确定情况下考虑再制造闭环供应链的生产决策和激励问题。Kemal[10]研究了随机需求下闭环供应链的协调问题，研究结果表明，在处理需求不确定问题时，下行风险值比其他风险评估工具有更好的效果。徐兵等[11]使用博弈论和条件风险值理论，讨论随机需求下生产商为风险中性，零售商为风险厌恶的闭环供应链。

关于销售竞争或回收竞争的文章也有很多，比如Huang M等[12]研究了闭环供应链中零售商回收与第三方回收的双重回收竞争问题，得出了回收竞争强度对供应链成员利益的影响规律。Ofek等[13]研究了消费者对旧产品的回收选择对零售商的定价策略、存储水平的影响。Majumder等[14]研究了当回收品会刺激新产品的市场需求时，第三方重新制造商促近竞争行为的方法。然而，上述研究竞争的文献中都是单方面从正向物流的销售竞争或者逆向物流的回收竞争考虑，而没有将二者同时考虑，然而现实生活中由于经济市场的激烈竞争，使得销售竞争和回收竞争同时存在的例子比比皆是。本文的主要工作即在闭环供应链中同时考虑销售和回收竞争，供应链由一个制造商和两个零售商组成，将制造商和两个不同零售商分别作为两个系统，研究这两个集中式供应链的最优定价策略，及定价受回收变化系数的影响，并有数值实验加以验证。

1 问题及模型

在此闭环供应链中，分别将制造商和两个带有竞争关系的零售商看作两个集中式的供应链系统，制造商使用原材料的制造成本为cm，由于地域经济和周边环境不同，两个互相竞争的零售商分别以不同的批发价p1,p2将产品卖给消费者，根据现实情况假设一部分使用过的产品可以由零售商回收，则逆向回收过程是两个不同的零售商以不同的回收价r1,r1将旧产品回收，而制造商可将得来的旧产品经过拆卸修理后重新制造成新产品再次销售，假设重新制造的成本费用cr小于原材料的制造成本cm，这样便达到回收重新制造可以节省企业制造成本、保护环境的双重目的。如同文献[5]假设消费者对产品的需求受双方零售价影响的关系为

Di(pi,pj)=αi-pi+βpj,(0≤β<1,i、j=1,2,i≠j)

(1)

式中:αi表示零售商i面对的市场规模;pi是零售商i的零售价;pj是他竞争对手的零售价;β是销售竞争系数。假设零售商i在逆向供应链中面对的回收函数是

Qi(ri,rj)=ai+ri-δrj,(0≤δ<1,i、j=1,2,i≠j)

(2)

式中：ai表示零售商i面对的回收市场规模;ri是零售商i付给消费者的回收价;rj是他竞争对手付给消费者的回收价;δ是回收竞争系数，反映废旧产品的回收市场上回收者的竞争强度。由于回收品来源于消费者市场对此类产品的需求，因此设回收品的市场规模ai和消费者的市场需求有如下关系：ai=γDi(pi,pj)，其中γ视为回收系数。文献[6]有类似的用法。根据市场实际，假设系数满足：0≤δ<β<1,0≤γ<β<1。

由上述问题假设及相关概念，在集中式下由一个制造商和两个带有竞争的零售商组成的供应链的系统利润可表示为

(cm-cr)Qi]

(3)

式中：(pi-cm)Di表示正向销售利润;riQi表示逆向回收付出的成本;(cm-cr)Qi表示对回收品重新制造所节省的成本。

2 模型求解及结果分析

此部分对模型(3)求解，并研究两个充满竞争的零售商的定价规律，即回收竞争系数对双方零售价及回收价的影响。

记重新制造的单位节省成本为Δ=cm-cr，此问题对应的数学规划模型为

(Δ-ri)Qi]

(4)

定理1 模型(4)中两个零售商的最优零售价p1、p2及两个最优回收价r1、r2分别为

i,j=1,2,i≠j

(5)

i,j=1,2,i≠j

(6)

证明：由式(4)可求系统利润函数Π(p1,p2,r1,r2)对决策变量p1、p2、r1、r2的二阶海赛矩阵：

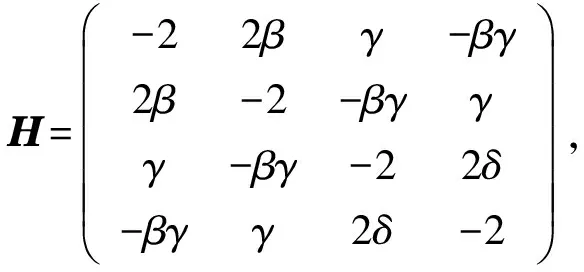
所以二阶海赛阵为负定矩阵，因此利润函数Π(p1,p2,r1,r2)关于决策变量p1、p2、r1、r2是凹函数，可由一阶条件求出稳定点即为利润函数的最优解。

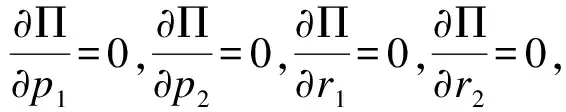
定理2 模型(4)中，两个零售商的零售价p1,p2分别关于回收竞争系数δ均为严格单调递减。

证明：由式(5)对δ求一阶导数得

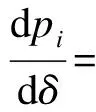
式中A=γ2(1-β)+4δ-4，B=4(1-δ)+γ2(1+β)。

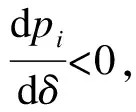
定理3 模型(4)中，两个零售商的零售价r1、r2分别关于回收竞争系数δ均为严格单调递增。

证明：由式(6)ri对δ求一阶导数得

式中A=γ2(1-β)+4δ-4，B=4(1-δ)+γ2(1+β)。

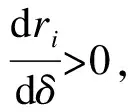
定理2和定理3表明当制造商和零售商组成的系统以利润最大为目标进行生产活动时，其最优零售价和回收价会受到市场中的一个重要参数回收竞争系数影响，具体的影响是销售价均与回收竞争系数负相关，而回收价均与回收竞争系数正相关，而回收竞争系数的大小反映了两个零售商回收竞争强度的大小。所以研究结果表明，两个零售商回收竞争强度越大，他们的零售价均会定的越低，而回收价格均会定的越高。这不但体现了现今竞争激烈的市场环境，而且给零售商和回收商提供了有规律的指导，比如在市场竞争环境不太激烈的乡镇，零售商可以将零售价定的较高，而回收商应以较低的回收价回收旧产品，这样便是最优的;相反在市场竞争环境激烈的市中心，零售商应适当降低零售价，而回收商可以较高的回收价回收旧产品。

3 数值实验

将一些参数取固定值，用数值实验对上述定理进行验证。不失一般性，本文取参数值如下：α1=100,α2=50,cm=20,Δ=10,γ=0.1,β=0.8，零售价和回收价随回收竞争系数的变化关系如图1所示。

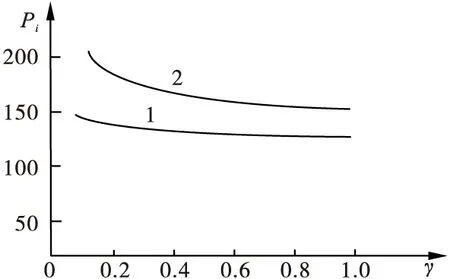
(a)零售价随回收竞争系数的变化

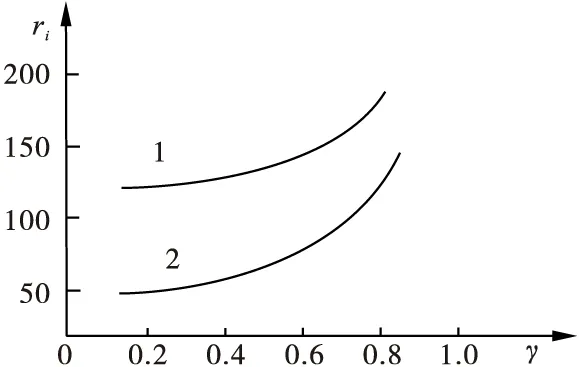
(b)回收价随回收竞争系数的变化

图中:曲线1分别表示零售商1对应的零售价和回收价p1、r1;曲线2分别表示零售商2对应的零售价和回收价p2、r2。

数值结果表明两个零售价随回收竞争系数的增大而降低，两个回收价随回收竞争系数的增大而提高，这与定理2及定理3的结论一致。

4 结束语

回收并重新制造是近年来企业十分关注的问题，这不单是环境保护的一种方式，而且对提高企业利润增强企业的核心竞争力有着不可估量的作用。本文在闭环供应链中同时考虑销售和回收双重竞争，研究市场参数δ对零售价和回收价的影响，研究结果也符合市场的实际情况，当市场竞争较为强烈时，零售商就会降价搞促销，而且抬高回收价用以回收更多旧产品进行重新制造节约成本。这也体现了如今竞争激烈的市场中定价决策规律。

[1]Kannan Govindan，Hamed Soleimani，Devika Kannan.Reverse logistics and closed-loop supply chain：A comprehensive review to explore the future[J].European Journal of Operational Research，2015，(240)：603-626.

[2]Y.Liang，S.Pokharel，G.H.Lim.Pricing used products for Remanufacturing[J].European Journal of Operational Research，2009，193(2)：390-395.

[3]R.C.Savaskan，S.Bhattacharya，L.N.Van Wassenhove.Closed-loop supply chain models with product remanufacturing[J].Management Science，2004，50(2)：239-252.

[4]洪宪培，王宗军，赵丹.闭环供应链定价模型与回收渠道选择决策[J].管理学报，2012，12(9)：1848-1855.

[5]Ma W，Zhao Z，Ke H.Dual-channel closed-loop supply chain with government consumptionsubsidy[J].European Journal of Operational Research，2013，(226)：221-227.

[6]Dekker R，Fleischmann M.Reverse logistics：quantitative models for closed-loop chains[M].Berlin：Springer，2004：4-5.

[7]Shantanu B.V，Daniel R.G.J，LukN.V.W.Optimal order quantities with remanufacturing across new product generations[J].Production and Operations Management，2006，15(3)：421-431.

[8]Shi J.M，Zhang G.Q，Sha J.C.Optimal production and pricing policy for a closed-loop system[J].Resources，Conservation and Recycling，2011，55(6)：639-647.

[9]Onur-Kaya.Incentive and production decisions for remanufacturing operations[J].European Journal of Operational Research，2010，(201)：442-453.

[10]Kemal S.A case-oriented approach to a lead/acid battery closed-loop supply chain network design under risk and uncertainty[J].Journal of Manufacturing Systems，2014.doi：10.1016/j.jmsy，2014.07.013

[11]徐兵，贾艳丽.基于CVaR准则的闭环供应链决策模型与协调研究[J].西南交通大学学报,2013，48(4)：715-723.

[12]Huang M，Song M，Lee L.H，et al.Analysis for strategy of closed-loop supply chain with dual recycling channel[J].International Journal of Production Economics，2013，144(2)：510-520.

[13]Ofek E,Katona Z,Sarvary M.Bricks and clicks’：the impact of product returns on the strategies of multichannel Retailers[J].Marketing Science，2011，30(1)：42-60.

[14]Majumder P,Groenevelt H.Competition in remanufacturing[J].Production and Operations Management，2001，10(2)：125-141.

(责任编辑：马金发)

Strategic Analysis of Supply Chain System’s Pricing Based on Dual Competition

LI Yang1，QU Tieping1，LI Huiling2

(1.Shenyang Ligong University，Shenyang 110159，China;2.The first private high school of Shenyang，Shenyang 110043，China)

In a closed-loop supply chain consisting of one manufacturer and two retailers,there exists two retailers’ retailing and recycling competition for the homogeneous product.We see the manufacturer and the two retailers respectively as two systems,and study the two centralized supply chain systems’optimal pricing strategy.We also study how the recycling competitive coefficient affects the price.The results show that the two systems’ retailing prices decrease with respect to the recycling competitive coefficient and the returning prices increase with respect to the recycling competitive coefficient.

supply chain;double competition;pricing strategy

2015-03-02

李扬(1981—)，男，讲师，研究方向：应用数学；通讯作者：曲铁平(1960—)，男，副教授，研究方向：基础数学.

1003-1251(2015)04-0055-04

F252.2

A