基于离散粒子群算法的应急救灾物资配送问题

宫 华,张 彪

(沈阳理工大学 理学院，辽宁 沈阳 110159)

基于离散粒子群算法的应急救灾物资配送问题

宫 华,张 彪

(沈阳理工大学 理学院，辽宁 沈阳 110159)

研究自然灾害下应急物流中的救援物资配送调度问题，在多种运输工具衔接以及救援物资分配考虑的基础上，建立物资运输与物资分配的两阶段优化模型。目标是最小化运输成本与未满足的需求量。运用离散粒子群算法进行模型的求解与仿真，结果证明了算法的有效性与稳定性，能够为应急物流物资运输及分配提供有效方案。

应急物流；物资运输；物资分配；离散粒子群算法

自然灾害主要包括气象灾害、地震灾害、水旱灾害、地质灾害、森林草原火灾等，大规模自然灾害的频发使得应急物流成为近年来应急管理研究中的一个新课题。灾害发生后重点考虑如何迅速及时地将大量应急物资运送到灾区配送中心，再由配送中心运往受灾地。自然灾害情况下的应急物资配送不同于常规的物流活动，具有信息不确定，物资需求量大等特点，着重满足应急物流中物资运输和调度的时效性、突发性和弱经济性要求。

近年来对于应急物流中的物资配送问题，国内外学者进行了大量的研究。Sheu[1]以自然灾害下的快速响应为背景，基于受灾点聚类研究应急物资的调配。Chang等[2]以最小化物资未满足量、延误时间及运输费用为目标，根据受灾点对物资需求的变化研究应急物资调度。Najafi等[3]针对震后响应阶段的物资调配建立多目标鲁棒优化模型，考虑多种运输方式、多种物资多阶段的随机模型。Ali等人[4]研究了在不确定环境下应急物资的调配，将物资的需求和供给以及运送的费用，运送中心损害均考虑为不确定因素。Zheng等[5]使用一种协同模糊优化方法研究应急物流中的运输计划问题，综合不确定性考虑三种运输方式衔接。

对应急物流的研究大多集中在救援的某一个环节上，而较少考虑震后应急物流这一全过程的物资运输及物资分配。本文以自然灾害为背景研究救灾物资配送问题，分多种方式运输调度、物资分配两阶段进行救援物资配送的决策。第一阶段综合考虑三种运输方式：直升机、火车、汽车，及灾后的实际路况，为各受灾点决策以何种运输方式向该地运输救援物资；第二阶段综合考虑各受灾点的受灾人数、物资需求量，为各受灾点决策救援物资分配。

1 模型的建立

1.1 模型描述

灾害发生后，决策者应在最快的时间内根据受灾情况制定救援物资配送方案。第一阶段为物资运输调度阶段，运输方式包括：直升机、火车、汽车，对于三种运输方式的决策以最小化运输成本及运输效率为目标。第二阶段为物资分配阶段，在救援物资运输调度确定的基础上，决策为各受灾点救援物资的分配。目标函数为最小化受灾点未满足的需求量，即受灾点人均缺乏的物资数和受灾点转运伤员所缺乏的救援工具数(当直升机、火车、汽车装载着物资到达受灾点之后，可继续作为转运伤员的工具)。根据决策者得到的各受灾点数据，考虑上述两个指标，并为各受灾点赋予不同的权值，进而决策出能够使现有救援物资发挥最大作用的救援调度方案。

1.2 符号说明

W：救援物资集散中心物资总量；

N：受灾点个数；

p=1、2、3，1代表直升机，2代表火车，3代表汽车；

ei：第i个阶段的权重，i=1,2；

L：三种运输方式均可达到的受灾点个数，满足L≤N；

βlp：第l个受灾点使用第p种运输方式的风险值；

dlp：使用第p种运输方式从中心到第l个受灾点需要行驶的距离；

tlp(clp)：使用第p种运输方式从中心到第l个受灾点的时间(单位行驶距离成本)；

gl：第l个受灾点等待救援的单位时间造成的经济成本；

ωlp(Wlp)：由第p种方式运输救援物资的第l个受灾点的权值(所需的救援物资数)；

Zp：救援物资集散中心当前可调度的第p种救援工具的数量；

Z1p：第p种救援工具的运力；

alp(blp)：第l个受灾点缺少第p种方式救援引起的转运伤员(物资)单位数量损失；

ulp：派往第l个受灾点使用第p种方式的运输工具数量；

Mlp：使用第p种方式的第l个受灾点的人均物资缺乏数量；

Olp：使用第p种方式的第l个受灾点转运伤员所缺乏的救援工具数量。

1.3 模型建立

mine1f1+e2f2

(1)

式中：

(2)

(3)

约束条件：

(4)

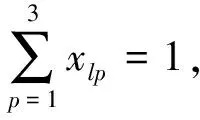
(5)

(6)

(7)

ulpZ1p≤Wlp;∀l∈Zp,p=1,2,3

(8)

Mlp=max{0,Wlp-ulpZ1p};∀l∈Zp,p=1,2,3

(9)

Qlp=max{0,Wlp/Z1p-ulp};∀l∈Zp,p=1,2,3

(10)

模型说明：式(1) 为总目标函数。式(2) 为第一阶段目标函数，最小化总运输时间成本(即受灾点等待第一批物资到达的时间)以及运输费用成本。式(3) 为第二阶段目标函数，最小化所有受灾点的未满足需求量，包括人均物资缺乏量引起的费用损失以及转运伤员的运输工具缺乏量引起的损失。式(4) 为所有运输数量的约束；式(5)表示三种方式均可采用的受灾点只采用其中一种方式。式(6)表示每种运输工具数量的可调度约束。式(7)表示救援物资集散中心在当前物资可调度量基础上进行分配，允许有剩余。式(8)表示各受灾点所需救援物资满足条件。式(9)、(10)表示人均物资缺乏数量和转运伤员所缺乏的救援工具数量。

2 算法设计

粒子群算法[6-7]是近些年应用比较广泛的一种智能算法，计算简单，收敛速度快。离散粒子群算法，其速度更新公式与原始PSO算法一样：

(11)

式中ω为惯性权重，表示粒子更新过程对上一代的依赖程度，采用如下线性变化公式进行更新效果更佳：

ω=ωmax-(k×(ωmax-ωmin))/Dmax

(12)

式中：ωmax为最大权重值0.9；ωmin为最小权重值0.1；k为当前迭代次数；Dmax为最大迭代次数。针对应急物资配送模型，本文提出采用两种不同编码方式的离散粒子群算法对运输调度及物资分配两个阶段进行求解，为决策者提供可行性较高的救援安排方案。

2.1 第一阶段

第一阶段运输调度中，采用二进制编码的离散粒子群算法简称BPSO。将粒子设计为一个XL×p的0-1矩阵，xlp=1表示第l个受灾点使用第p种运输方式，xlp=0表示不采用。按照初始解的规则产生一个粒子种群，依照速度和位置更新在解空间搜索寻优，直至算法结束找到适应度最高的粒子。初始种群的产生要满足随机性及解的可行性，初始解产生规则如下：

Step 1 将1,0,0三个数字全排列，A，B，C为三个矩阵，其中A=[1,0,0]；B=perms(A)；C共有6行，每一行是1,0,0的一个全排列；

Step 2 初始解设为X=zeros(L,p);L为地点数目，p为运输方式的种类；

Step 3 产生1～6的随机数，存储在c向量：a=rand(1,6)；b=a×5+1；c=floor(b)；

Step 4 以c中第一个数字作为角标，取出B中对应行的数据作为X中的第一行数据，以此类推，便可生成初始解X。

为表示速度值是二进制位取1的概率，速度值采用sigmoid函数被映射到区间[0,l]：

(13)

s(vid)表示位置xlp取1的概率，通过下式改变粒子的位值

(14)

规定速度的范围[-vmax,vmax]，根据经验值，文中取vmax=4。

本文采用改进的BPSO算法[8]：将sigmoid函数表达式作如下修改：

(15)

对粒子的位值改变函数作修改：

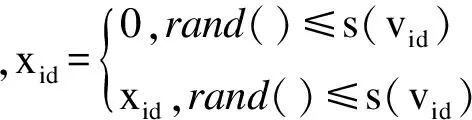
(16)

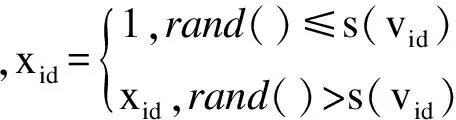
(17)

此时算法收敛速度较快，局部搜索能力强,但全局搜索能力变弱。为使算法后期具有较强的局部搜索能力，仍需要对上述改进的BPSO算法继续改进。

Ifk<γ×Dmax选用式(13)、式(14)进行粒子位置更新；

Else 选用式(15)、式( 16)、式(17)进行粒子位置更新。

其中k为当前迭代次数，γ为系数，取值范围为[0,1]。

2.2 第二阶段

物资分配中，采用自然数编码的离散粒子群算法，其核心在于对粒子位置进行取整计算。将粒子设计为一个Ip维向量，Ip为使用第p种运输方式的地点个数，向量中元素均为自然数，其和为救援物资集散中心当前可调度的第p种运输工具的数量Zp。按照初始解的规则产生一个粒子种群，依照速度和位置更新方式在解空间搜索寻优，直至算法结束找到适应度最高的粒子。

初始解产生：

Step 1 随机产生Ip个(0,1)内的随机数，存入a向量：a=rand(1,Ip)；

Step 2 对a中所有元素求和记为b，计算a中每个元素与b的比值，结果存入c向量：b=sum(a)；c(i)=a(i)/b；

Step 3 救援物资集散中心当前可调度的第p种运输工具数量为Zp，将c中每个元素与Zp相乘，结果存入向量d:d(i)=c(i)×Zp;

Step 4 对d中各元素取整，结果存入向量e：e(i)=round(d(i))；

Step 5 判断e中元素之和是否等于第p种运输工具数量Zp，若不等于则重复Step 1～4，若等于则e中数据即为一个初始解。

速度更新公式为式(11)，位置更新公式如下：

(18)

之后对位置进行取整操作：

(19)

3 模型求解

3.1 数值算例

为验证离散粒子群算法性能，在Matlab 7.0平台上进行仿真实验。以土耳其地震灾区为例，地震灾区有1个救援物资集散点，8个受灾点。采用直升机运输的受灾点5个，直升机运力13架次；采用火车运输的受灾点4个，火车运力12节车厢；采用汽车运输的受灾点8个，汽车运力50辆。算法参数设置如下：最大迭代次数1 000次，粒子群规模20，学习因子c1,c2均为2。其他参数如表1～表4所示。

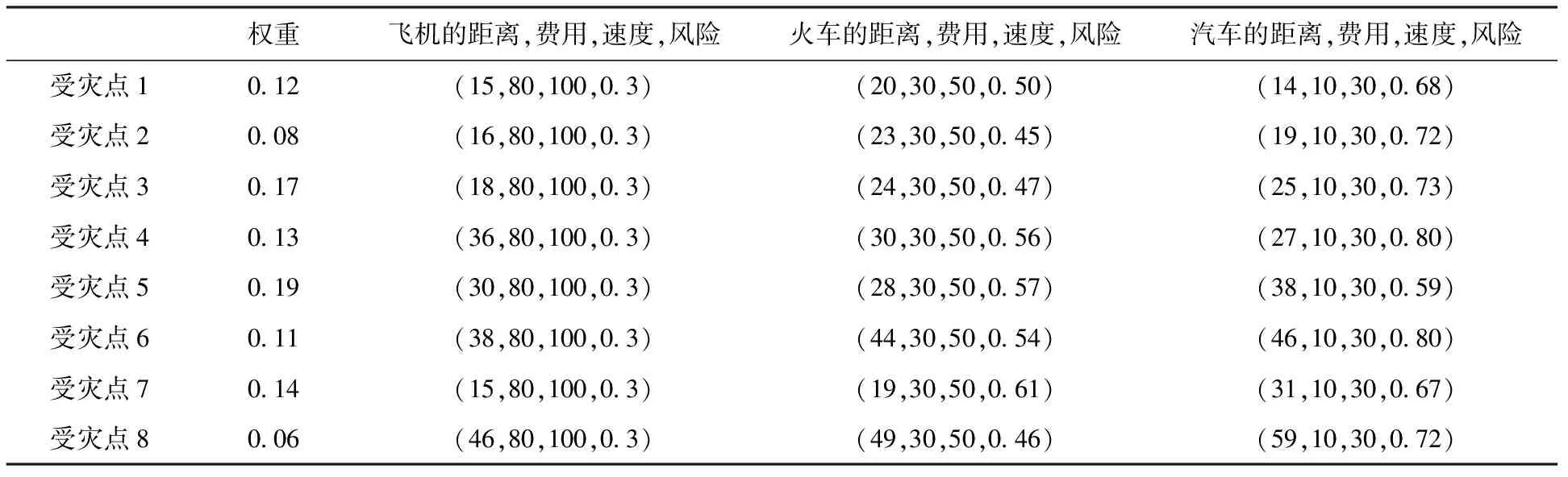
表1 三种方式均可采用的受灾点参数表

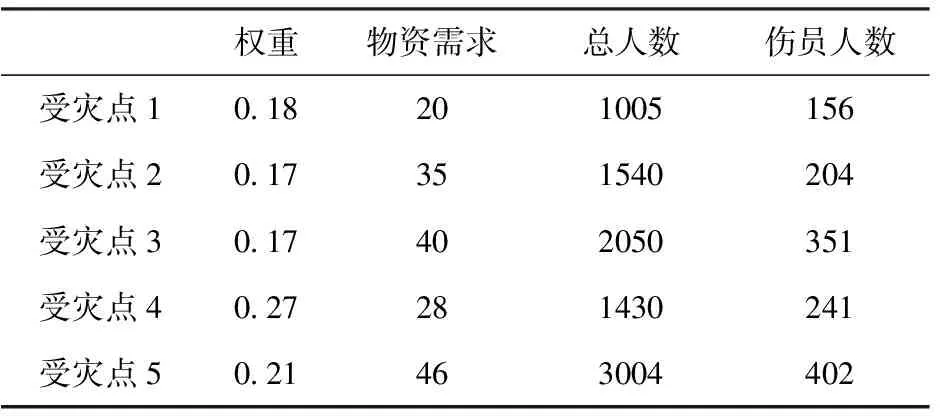
表2 使用直升机运输的各受灾点参数表

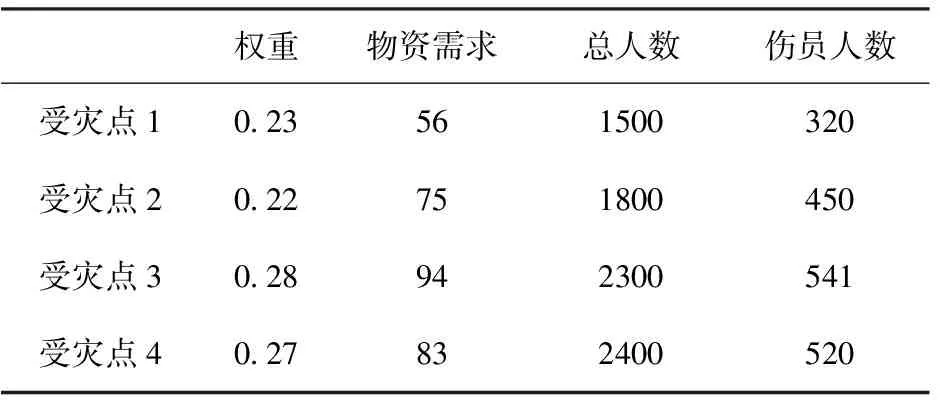
表3 使用火车运输的各受灾点参数表

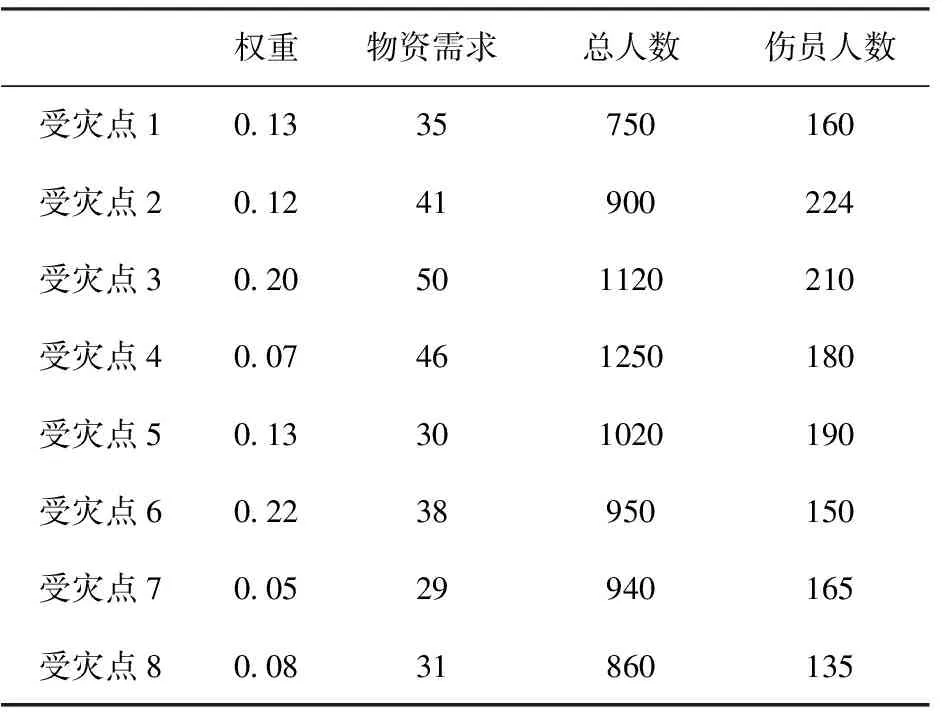
表4 使用汽车运输的各受灾点参数表

3.2 求解结果

第一阶段运输调度求解过程及结果如图1、表5所示。

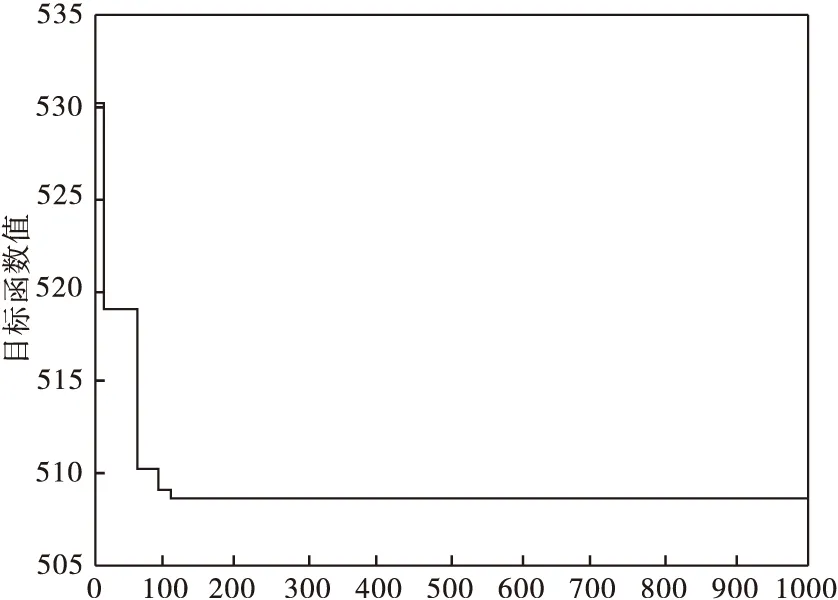
图1 第一阶段求解过程示意图

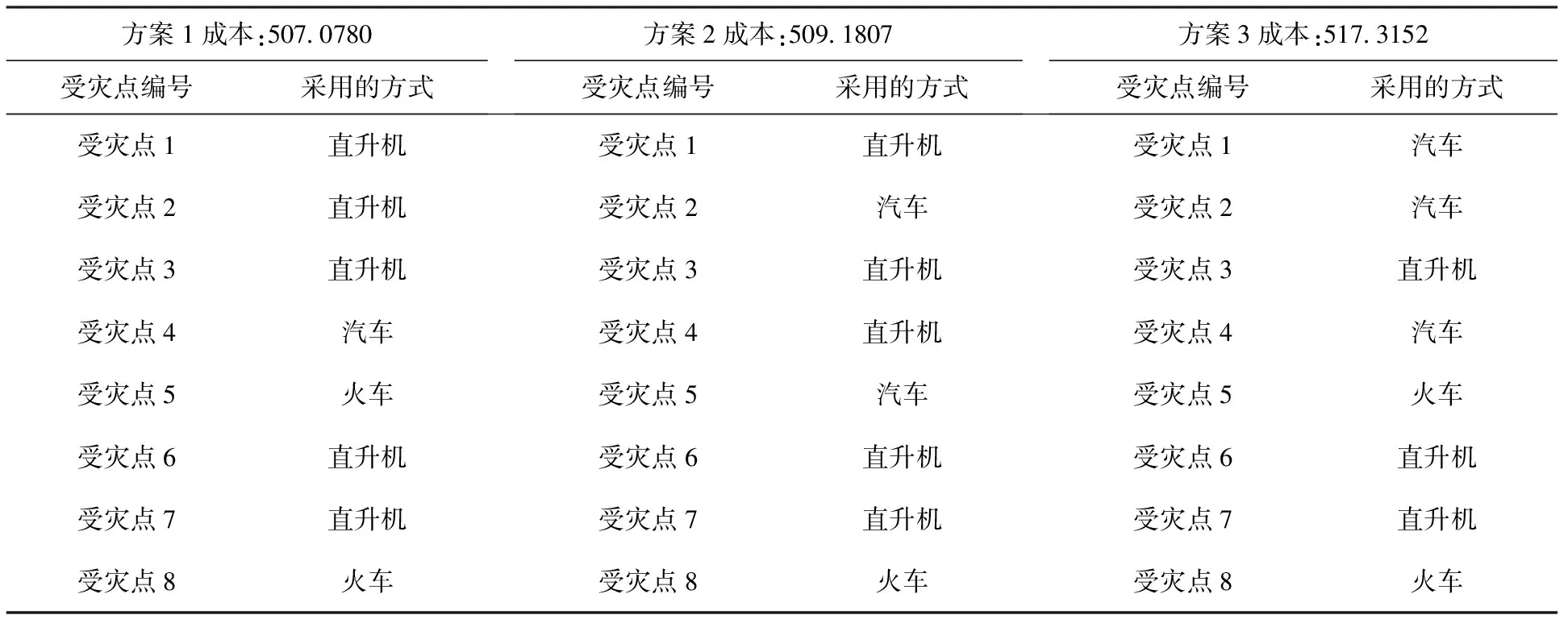
表5 第一阶段三种决策方案

第二阶段汽车、直升机和火车运输物资分配方案求解过程及结果如图2、表6～表8所示。

由此可得，两个子目标分别给出了三个参考解，方案1中：f1=507.07，f2=3922.9；方案2中：f1=509.18，f2=4033.9；方案3中：f1=517.31，f2=4055.8。对于总目标e1f1+e2f2，子问题的权重分别为0.4,0.6，可以求得最小目标值e1f1+e2f2=2556.57；相应救援方案为：第一阶段在8个受灾点中选出第1、2、3、6、7个采用直升机运输，第5、8个采用火车，第4个采用汽车；第二阶段从集散点向5个受灾点派直升机救援，采用方案1；向4个受灾点派火车救援，采用方案1；向8个受灾点派汽车运输，采用方案1。

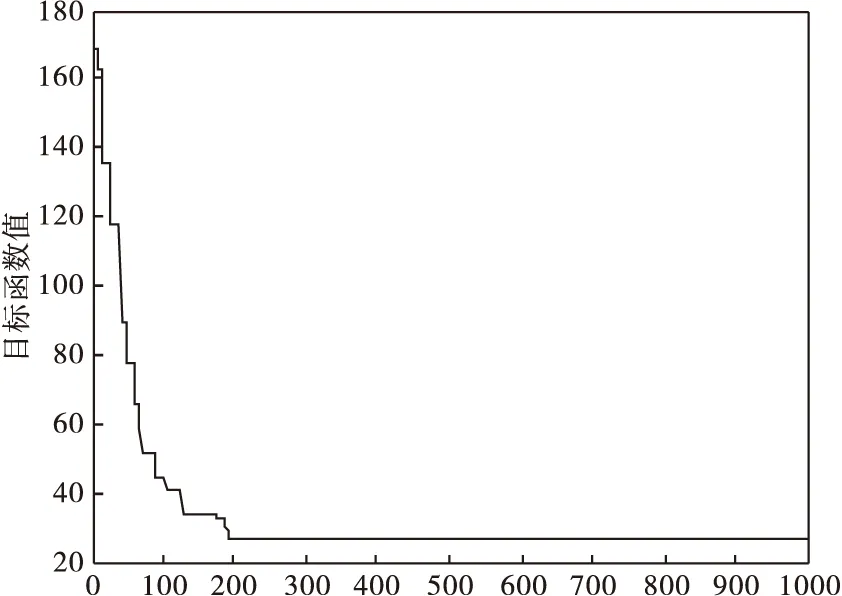
图2 汽车运输救援物资分配方案求解过程示意图

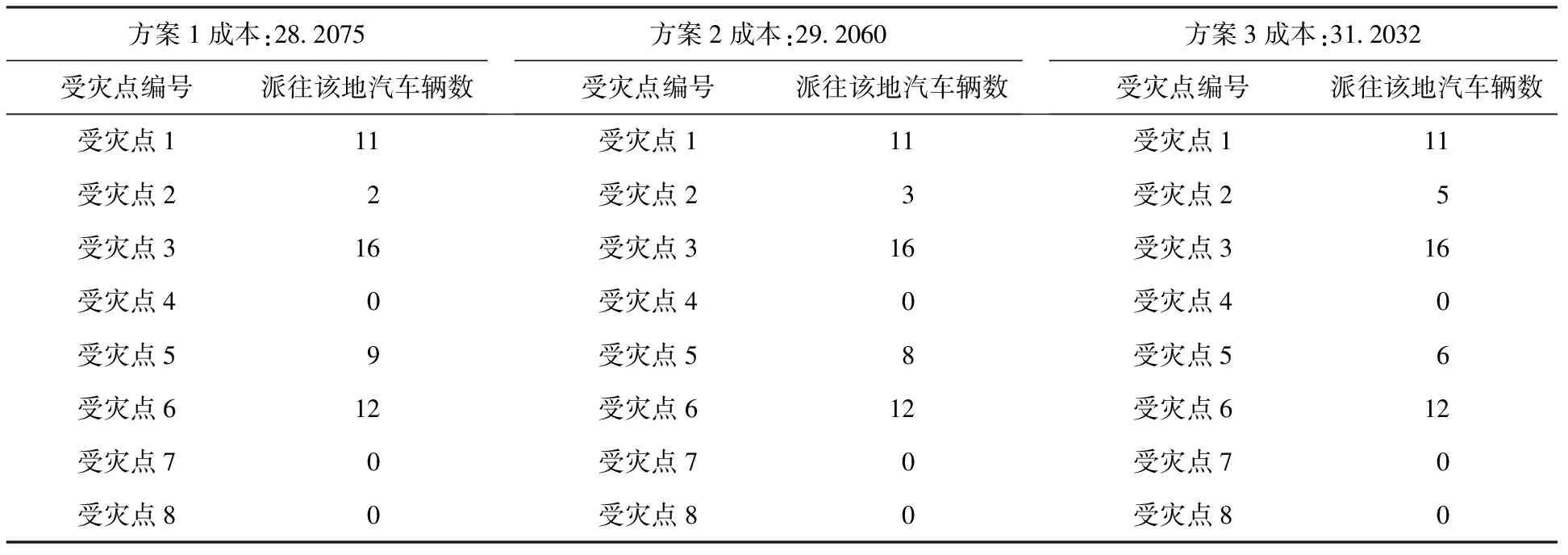
表6 汽车运输救援物资的三种分配方案

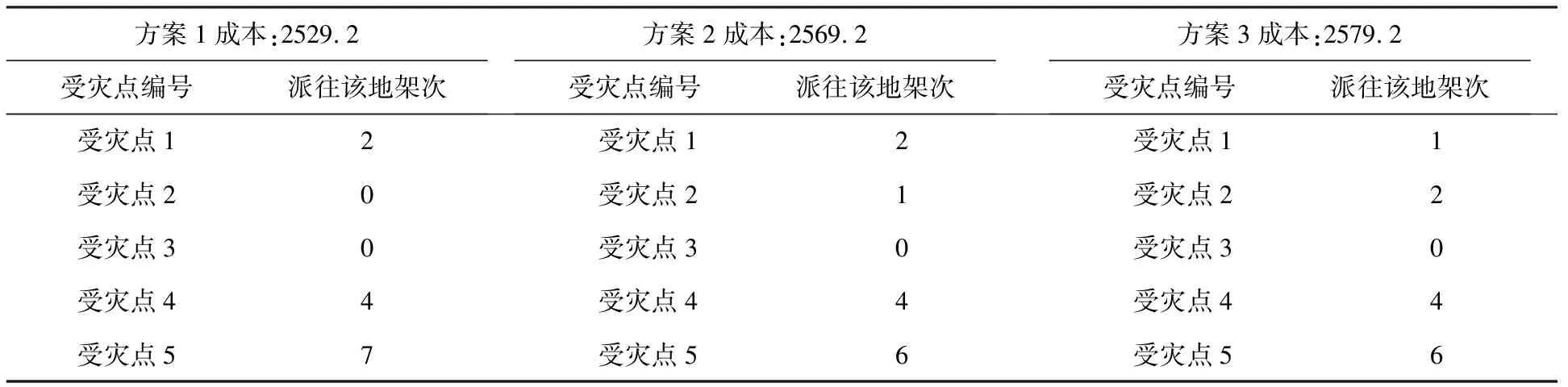
表7 直升机运输救援物资的三种分配方案

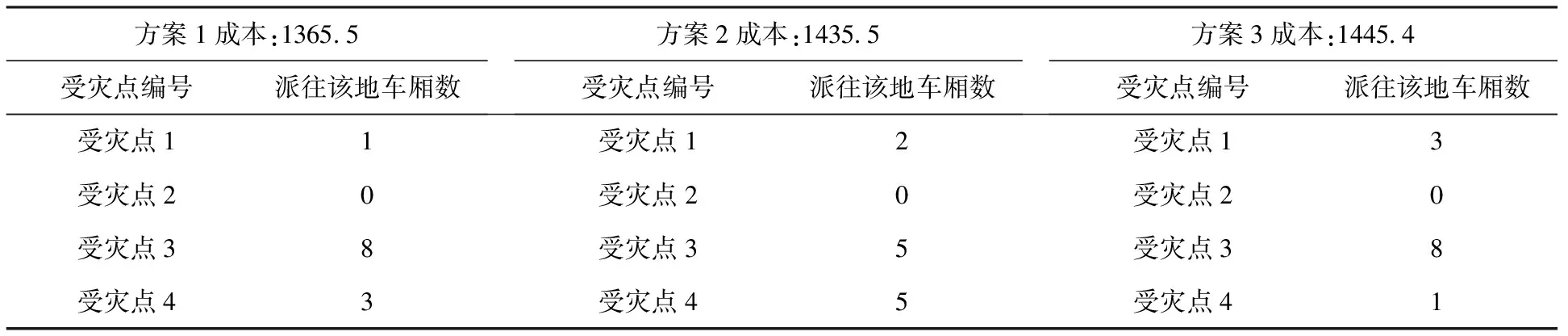
表8 火车运输救援物资的三种分配方案

4 结束语

以自然灾害为背景，建立应急物资运输及分配的两阶段优化模型，第一阶段以运输成本最小化为目标，决策运输工具的使用；第二阶段在确定应急物资运输方案后，以未满足的需求量最小化为目标，研究救援物资分配问题。基于离散粒子群算法，分别采用二进制和自然数编码设计算法。仿真结果证明了算法的有效性与稳定性。对于应急物流调度，可以进一步研究按照物资需求随时间的变化进行划分救援过程，汽车在地震发生后的行驶时间的随机性，以及汽车运送救援物资时的路径选择等问题。

[1]Sheu J B.An emergency logistics distribution approach for quick response to urgent relief demand in disasters[J].Transportation Research Part E,2007,43(6):687-709.

[2]Chang F S,Wu J S,Lee C N,et al.Greedy-search-based multi-objective genetic algorithm for emergency logistics scheduling[J].Expert Systems with Applications,2014,41(6):2947-2956.

[3]Najafi M,Eshghi K,Dullaert W.A multi-objective robust optimization model for logistics planning in the earthquake response phase[J].Transportation Research Part E,2013,49(1):217-249.

[4]Ali B A,Mohammad S J,Mehdi A,et al.A modified particle swarm optimization for disaster relief logistics under uncertain environment[J].The International Journal of Advanced Manufacturing Technology,2012,60(4):357-371.

[5]Zheng Y J,Ling H F.Emergency transportation planning in disaster relief supply chain management:a cooperative fuzzy optimization approach[J].Soft Computing,2013,17(7):1301-1314.

[6]Kennedy J,Eberhart R C.Particle swarm optimization[C].In proceedings of IEEE International Conference on Neural Networks,IV.Pis-cataway,NJ:IEEE Service Center,1995:1942-1948.

[7]Kennedy J,Eberhart R C.A discrete binary version of the particle swarm algorithm[C].In proceeding of the World Multi conference Systemics,Cybemeties and Information,NJ:Pis-cataway,1997:4104-4108.

[8]刘建华.粒子群算法的基本理论及其改进研究[D].长沙:中南大学,2009.

(责任编辑：马金发)

An Emergency Relief Supplies Distribution Problem Based on the Discrete Particle Swarm Optimization Algorithm

GONG Hua，ZHANG Biao

(Shenyang Ligong University,Shenyang 110159,China)

A relief supplies distribution problem in emergency logistics in the natural disasters is studied.A two-stage supplies optimization model of transportation and allocation is considered that takes into consideration the connection of various transportation facilities and the allocation of the relief supplies.The objective is to minimize transportation cost and the unmet demand.A discrete particle swarm optimization algorithm is applied to solve the model.The simulation results show the effective and stability of the proposed algorithm and provide the scheme of transportation and allocation for the emergency supplies.

emergency logistics;supplies transportation;supplies allocation;DPSO

2015-01-04

国家自然科学基金资助项目(71101097)；辽宁省“百千万人才工程”培养资助项目(2014921043)

宫华(1976—)，女，副教授，博士，研究方向：生产调度与物流优化.

1003-1251(2015)02-0065-06

O224

A