禁忌搜索的单机总加权拖期最小化问题
郭 宇,曲铁平
(沈阳理工大学 理学院,辽宁 沈阳 110159)
禁忌搜索的单机总加权拖期最小化问题
郭 宇,曲铁平
(沈阳理工大学 理学院,辽宁 沈阳 110159)
总加权拖期最小化(SMTWT)的单机调度问题是一个NP难问题,特别是当问题规模较大时,其求解时间面临巨大的挑战。提出采用禁忌搜索(TS)算法进行求解。首先介绍了禁忌搜索算法的原理及影响其性能的关键因素,进而针对本问题设计了定制化的禁忌搜索算法。最后通过60组基准问题对算法的性能进行了测试。实验结果证明本算法可行且所得结果质量较高。
单机调度;加权拖期;禁忌搜索
SMTWT问题已经被证明是一个NP难问题[1],特别是当工件个数超过50件时,常用的优化方法如动态规划方法、分支定界方法等都难以对其进行求解[2]。同时,也没有统一的分配规则适用于所有的问题,比如对于最多只有一个工件延迟的调度问题,可以由EDD规则给出最优排序,而对于所有工件都发生延迟的调度问题,可以由WSPT规则给出最优排序。因此,对于负荷较低的调度问题,EDD规则会给出较好的解,而对于负荷较重的调度问题,则可以通过WSPT规则获得较好的解。有很多启发式算法[3-6]就是利用这一思想。本文针对问题特点设计了禁忌搜索算法进行求解。
1 应用禁忌搜索算法求解SMTWT问题
1.1 SMTWT问题描述

1.2 禁忌搜索算法原理
禁忌搜索算法最早由Glover在1986年提出,其本质上是对局部搜索的一种拓展,是一种全局搜索的方法[2]。通过模拟人类的记忆机制,采用禁忌策略避免重复搜索,同时也可避免搜索过程陷入局部最优。同时采用解禁准则来释放已经被禁忌的优良状态,以保证搜索过程的有效性和多样性。TS算法可以克服搜索过程早熟的缺陷从而达到全局最优。禁忌搜索算法的求解过程可描述为:首先获得一个初始解,然后搜索其邻域内的最优解,并判断是否满足事先给定的终止准则,若满足,则输出最优解,否则,继续迭代直至满足终止准则。同时为避免重复搜索或是陷入局部最优,引入一个禁忌表用于记录已经搜索过的局部最优解以及曾经搜索的路径,将其作为下次搜索的依据。禁忌搜索算法流程如图1所示。

图1 禁忌搜索算法流程图
1.3 SMTWT问题的禁忌搜索算法实现
针对禁忌搜索算法的四大关键因素设计求解SMTWT问题如下:
1)初始解的获得:在本算法中,用1,…,n的一个排列表示一组解,即n个工件的一种加工顺序。同时采用EDD准则获取初始解,其中EDD准则即是按照交货期从前到后对工件进行排序。
2)邻域的构造:常用的构造邻域的方法包括插入和交换两种操作。本文采用交换两工件的位置来构造当前解的邻域集。
3)禁忌对象:文中将“弧”作为禁忌对象。在一个排序中,若工件i-1在工件前,则定义为一条弧((i-1),i)。如果当前的操作为交换工件i与工件j的位置,则将弧((i-1),i)、((j-1),j)及(j,(j+1))作为禁忌对象,将其加入到禁忌表中。
4)候选解策略:如果在当前解的整个邻域内寻优,会导致计算量过大,降低整个算法的求解速度,因此,需设定一个搜索策略以缩小搜索范围。文中将基于如下性质选择候选解:在SMTWT问题中,对于工件i与工件j,若满足dj≤Ci,ωj≥ωi,pj≤pi,则在最优排序中,工件j将优先于工件i。
2 数据测试
为了测试算法的有效性,本文从OR数据库中选取60组基准问题(benchmark problem)进行测试,其中针对40个工件的问题30组,针对50个工件的问题20组,针对100个工件的问题10组,参数设置为:终止迭代次数40次,禁忌表长度7,候选解集大小20。实验结果显示,对包含40个工件的问题,平均迭代8次即可获得最优解,对包含50个工件的问题,80%可获得最优解,且平均迭代次数为40次,而对于包含100个工件的问题,经40次迭代之后也能获得相对误差低于1%的近优解。对于每一组测试,本文基于平均相对误差(averagerelative percent deviation,ARPD)与不能求得最优解的问题个数(the number of non-optimal,NO)两个标准对该算法进行评价,对比结果如表1所示。该实验结果表明,本文提出的禁忌搜索算法在求解中小规模的单机调度问题时可获得最优解,在求解大规模单机调度问题时也可在短时间内获得令人满意的近优解。
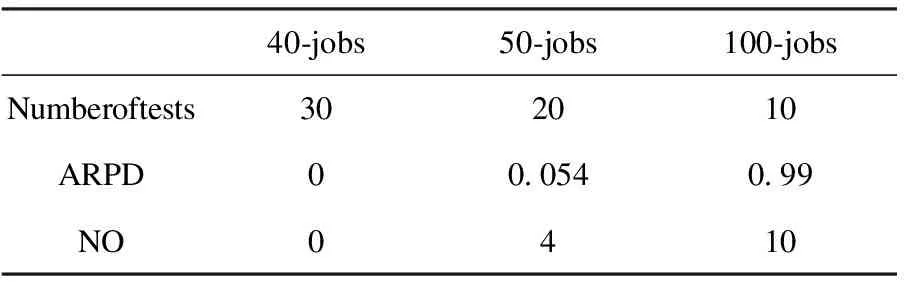
表1 对比结果
3 结论
采用禁忌搜索算法求解SMTWT问题。针对一组基准问题,可获得高质量的解。结果表明,针对40个和50个工件的问题,获得最优解的比例分别可以达到100%以及80%,对于100个工件的问题,相对误差率也仅有0.99%。这说明该算法对于大规模的SMTWT问题也可以获得质量较高的解。
[1]Du Jianzhong,Q.Leung,Joseph Y.T.Minimizing total tardiness on one machine is NP-hard[J].Mathematics of Operations Research,1990,15(3):483-495.
[2]Abdul-Razaq,L.Potts,Van Wassenhove.A survey of algorithms for the single machine total weighted tardiness scheduling problem[J].Discrete Applied Mathematics,1990,26(2-3):235-253.
[3]Carroll D.C.Heuristic Sequencing of Single and Multiple Components[J].European Journal of Operational Research,1999,165(3):423-443.
[4]Montagne JR,Crauwels ER.Sequencing with time delay costs[J].Industrial Engineering Research,2001,32(2):26-38.
[5]Morton TE,Rachamadugu ECY.Vesalainen.Accurate Myopic Heuristics for Tardiness Scheduling[J].Annals of Discrete Mathematics,2005,45(4):343-362.
[6]Koulamas C.The total tardiness problem:Review and extensions[J].Operations Research,1994,42(2):1025-1041.
(责任编辑:马金发)
A Tabu Search Algorithm for SMTWT
GUO Yu,QU Tieping
(Shenyang Ligong University,Shenyang 110159,China)
The single machine total weighted tardiness problem (SMTWT) is a NP-hard problem.The problem is extremely time-consuming,especially when jobs number is beyond 50.TS algorithm is presented to solve it.Firstly,the theory and the key elements of general TS are demonstrated.Then a set of specific strategies is devised for SMTWT.At last,60 benchmark problems are tested for examining the algorithm performance.Simulation results indicate that the algorithm is feasible and it could obtain better value.
single machine scheduling;weighted tardiness;tabu search
2014-12-04
郭宇(1981—),女,讲师,研究方向:机组调度,智能优化。
1003-1251(2015)03-0021-03
TP301.6
A

