综合机械化固体充填开采控制覆岩变形的力学分析

曹正正，姜海林，黄秀文，周跃进

(1.中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州221116; 2.中国矿业大学力学与建筑工程学院，江苏徐州221116)



综合机械化固体充填开采控制覆岩变形的力学分析

曹正正1，2，姜海林2，黄秀文2，周跃进1

(1.中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州221116; 2.中国矿业大学力学与建筑工程学院，江苏徐州221116)

［摘要］建立固体充填开采下覆岩变形的对称层合板模型，提出模型的定解条件，得到覆岩变形的解析解。采用FLAC建立充填开采覆岩运动的数值计算模型，系统研究充填体密实度、煤层采厚和采深对覆岩变形的影响变化规律。研究表明:采厚和采深对覆岩变形的影响均呈现线性关系;充填体密实度对覆岩变形的影响更为明显。当密实度η＜75%时，覆岩变形较大;当密实度η＞75%时，覆岩变形量显著减小。研究结果可为固体充填开采理论研究与工艺设计提供参考。

［关键词］综合机械化固体充填开采;覆岩变形;对称层合板; FLAC

［引用格式］曹正正，姜海林，黄秀文，等.综合机械化固体充填开采控制覆岩变形的力学分析［J］.煤矿开采，2015，20 (2) : 70－74.

综合机械化固体充填开采技术是为了解决目前“三下”压煤难题以及合理处理煤矸石、粉煤灰等矿山废弃物而研发的一种安全高效采煤技术［1－4］，并且已经得到良好的推广和应用［5－8］。由于固体充填开采条件下的覆岩变形以及地表沉陷规律与全部垮落法开采显著不同［9－10］，因此必须深入研究固体充填采煤的覆岩变形的力学机理，建立相应的充填采煤岩层控制理论。

目前，在充填采煤岩层控制方面的研究主要集中在岩梁力学模型方面［11－12］，即将其归结于平面应变问题进行处理，这对于工作面中部区域符合的很好，但并不能很好地揭示工作面两端具体情况。因此，本文根据充填开采上覆岩层的变形特征，采用对称层合板力学模型对上覆岩层的变形进行求解，对固体充填开采条件下覆岩变形进行较为深入地分析。

1　充填开采覆岩变形的力学分析

1.1对称层合板力学模型

相对于全部垮落法开采，综合机械化固体密实充填开采可以有效地控制上覆岩层的变形和运动，上覆岩层间不会出现离层现象，覆岩仅产生微小的连续弯曲变形。根据覆岩分层结构和软硬相间的特征，将充填开采覆岩结构简化为多个各向同性岩层组成的对称层合板覆岩结构，如图1所示。覆岩结构上表面作用有表土层施加于覆岩的均匀分布载荷，覆岩结构的下表面支承于充填固体。

1.2覆岩变形的控制方程

在综合机械化固体密实充填采煤条件下，当覆岩发生弯曲变形时，由于岩层间紧密叠合，层状岩层间抗剪切力较弱，岩层发生同步变形，即各个岩层的曲率和扭率趋于一致，即:

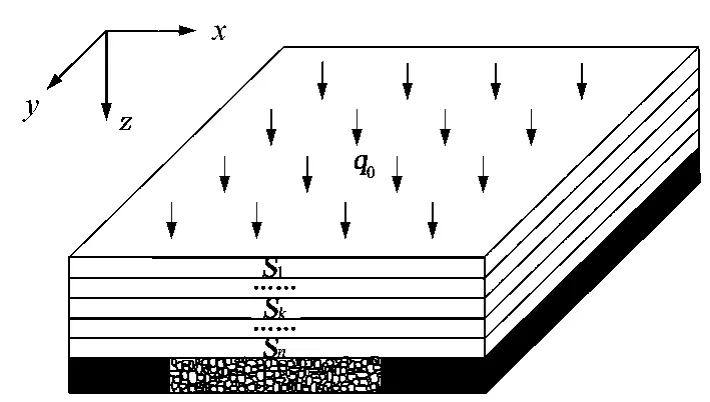
图1　充填开采覆岩结构的对称层合板模型

覆岩的变形曲率和扭率完全确定了覆岩所有各点的形变分量，称为岩层的形变分量［13］。岩层曲率和扭率为:

将式( 3)代入式( 1)和式( 2)，得到:

由于覆岩层合板结构在每个截面上的总弯矩和总扭矩都由覆岩层合板结构的单层岩层的各自小截面共同承担，即:

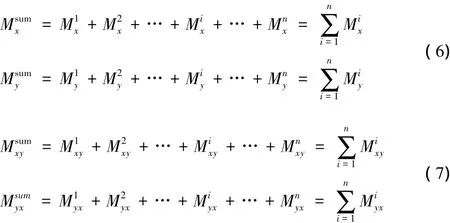
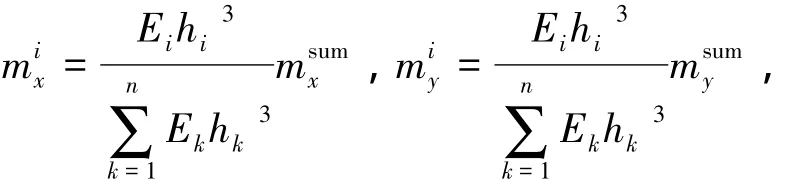
对于横截面单位长度上，第i个岩层内力用挠度wi表示如下［13］:

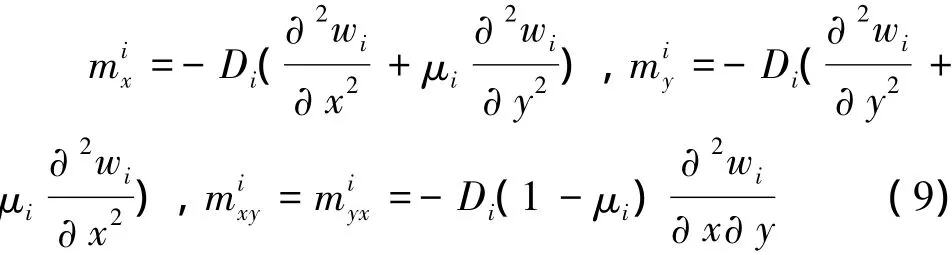
将式(9)代入式(8)中，得到:

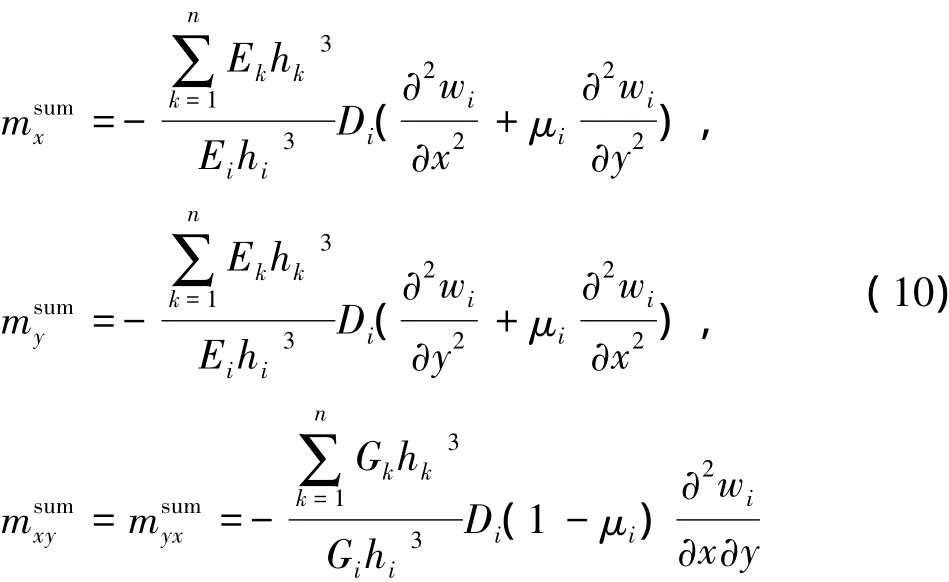
从对称层合板覆岩结构中取出h·dx·dy的六面体，根据覆岩结构的对称性，分别合成的主矢量均为0，因此，为了分析的方便，只画出覆岩层合板结构六面体的中面，并将载荷及横截面上内力加在中面上，如图2所示。

图2　覆岩层合板结构六面体中面示意

以通过微分块中心而平行于y轴和x轴的直线为矩轴，分别写出力矩的平衡方程，同时沿z方向列出力的平衡方程，进而联立化简可得:

设:

则:

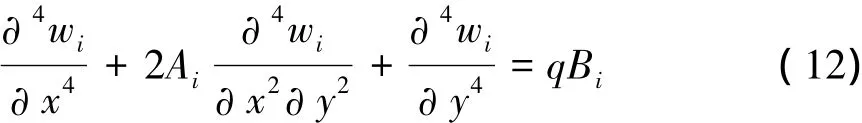
这就是基于对称层合板理论的覆岩变形控制微分方程。

一般而言，覆岩结构上的载荷q(x，y)包括两部分:一部分为覆岩表土层作用的载荷，可以简化为均布力q0;另一部分为充填体对覆岩结构的支撑作用力，根据文克勒弹性地基假设［14］，其数值为p =－kw，因此，覆岩结构上的载荷q(x，y)满足:

q(x，y) = q0+ p = q0－kw(13)

将式(13)代入式(12)，化简得到:

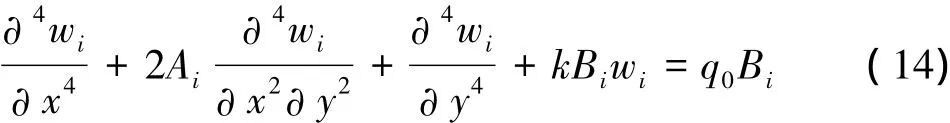
当煤层埋藏较浅时，其边界条件可以视为四边简支情况，将挠度表达式设为重三角级数:

将式(15)代入式(14)中，得到:

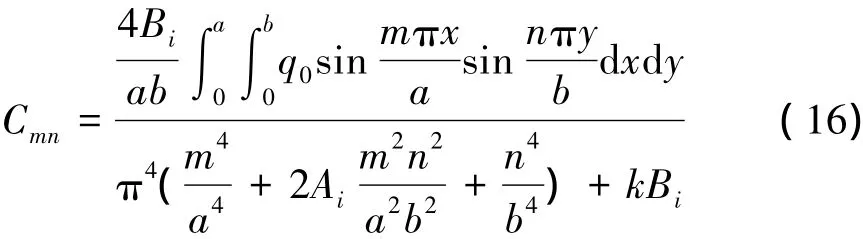
将式(16)代入式(14)，得到挠度wi表达式:

1.4算例分析

第三，辅助网络规划建设功能。这方面主要对系统技术指标进行确定，从而实现自动生成理论技术参数的目的，比如系统图、拓扑图等，通过对物理资源和逻辑资源的计算，完成对辅助功能的规划和设计，主要包括光节点位置、线缆路由、光缆交接位置以及传输机房等方面。辅助建设功能主要体现在网络实施期，对设计结果进行分析，从而计算工程需要的基本材料，利用电子派单的方式对材料的领用、补充和退还等，从而促进工作效率的提升，在很大程度上减少材料的不合理使用，同时缓解库存压力，有助于建设工程的顺利开展。

某固体充填试验区开采面的走向长度为800m，倾向长度为200m，煤层采厚为3m，煤层埋深为250m，其中表土层为150m，表土层平均容重γ为25000N/m3。表土层的重量可以简化为均布载荷q0，其值为q0=γd = 3.75MPa。上覆岩层厚度为100m。根据岩层实际条件，将上覆岩层简化为3层岩层组成对称层合板覆岩结构，其力学参数如表1所示。

取充填物的泊松比为0.4，弹性模量为0.35GPa。以第1层岩层为例，根据式(17)，利用数学软件Mathematica绘制上覆岩层的垂直位移场，如图3所示。

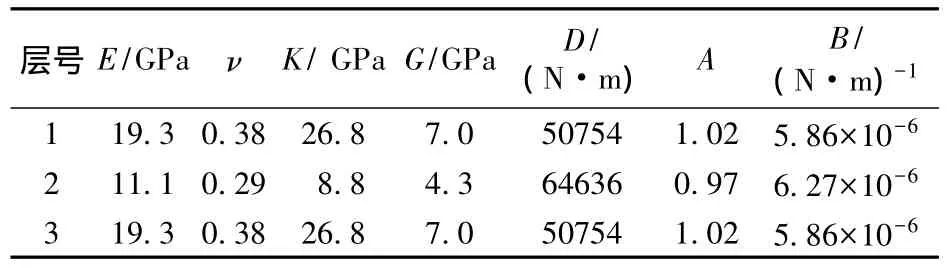
表1　覆岩结构的物理力学参数

图3　覆层的垂直位移场

以第1层岩层为例，根据式(17)，研究岩层中点垂直位移随充填体的弹性模量的变化规律。利用数学软件Mathematica绘制岩层中点垂直位移随充填体的弹性模量的变化曲线，如图4所示。

图4　岩层中点垂直位移随充填体的弹性模量的变化曲线

当充填体的弹性模量E = 0.2GPa时岩层中点垂直位移约为0.09m，随着充填体的弹性模量增加，岩层的垂直位移不断降低;当充填体的弹性模量增至1.5GPa时，岩层中点垂直位移为0.01m，相对于弹性模量E=0.2GPa时减少了近90%左右。由此可见，适当增大充填体弹性模量对控制覆岩变形是可行的。

在工程实践中，根据固体充填材料的应力应变规律测试结果［15］，可以换算出充填体弹性模量与充填体密实度之间的关系。因此，可以在充填方案中设计合理的充填体密实度，将覆岩变形和地表沉陷量控制在许可的范围之内。为了进一步研究充填体密实度、煤层采厚和煤层采深对覆岩变形的影响变化规律，下节将采用数值计算方法对此进行定量研究分析。

2　数值计算分析

2.1数值计算模型

2.1.1计算模型的建立

利用FLAC软件建立数值计算模型，以某矿工程地质条件为背景，各岩层物理力学参数如表2所示;根据固体充填材料的应力应变规律测试结果［15］，经换算得到充填体的K和G，充填体的力学参数如表3所示。

建立的数值计算力学模型尺寸为1400m× 390m，工作面推进由400m处到1000m处，工作面推进长度为600m。模型两侧约束水平方向位移，底部约束垂直方向位移。

表2　各岩层物理力学参数

表3　充填体力学参数

2.1.2数值计算方案

为了研究充填开采条件下覆岩变形规律，主要考虑充填体密实度、煤层采厚和煤层采深对覆岩变形的影响。数值计算方案如下:

方案1固定采厚为3m、采深为360m，分别取:η= 50%，60%，75%，80%，85%，95%，研究充填体密实度对覆岩变形的影响。

方案2固定充填体密实度为85%、采深为360m，变化采厚分别为: h = 2.5m，3m，3.5m，4m，4.5m，6m，研究煤层开采厚度对覆岩变形的影响。

方案3固定充填体密实度为85%、采厚为3m，变化采深分别为: H = 300m，350m，400m，450m，500m，550m，研究煤层开采深度对覆岩变形的影响。

2.2计算结果分析

2.2.1充填密实度对覆岩变形的影响

图5给出了不同充填体密实度时覆岩结构关键层下沉曲线，图6给出了不同充填密实度时覆岩结构关键层下沉量的变化曲线，可以看到:

图5　不同密实度时结构关键层下沉曲线

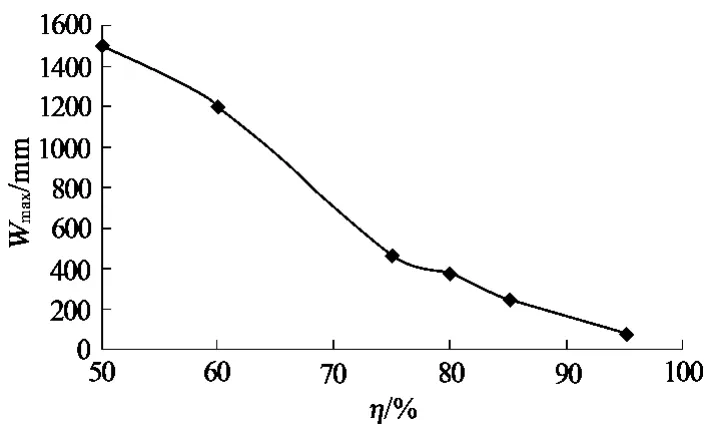
图6　结构关键层下沉量随密实率变化曲线

(1)当充填体的密实度分别为η= 50%，η= 60%时，随着工作面的推进，工作面围岩破坏区域高度随之增大，覆岩结构关键层仍有较大的下沉变形。

(2)当充填密实度η＞75%时，覆岩结构关键层仅呈现较小的连续弯曲变形。当充填密实度由50%增大到75%时，覆岩结构关键层从1500mm减小到467mm，减小了1033mm。

2.2.2采厚对覆岩变形的影响

图7给出了不同采厚时覆岩结构关键层下沉变形曲线，图8给出了不同采厚时覆岩结构关键层下沉量的变化曲线。可以看到:

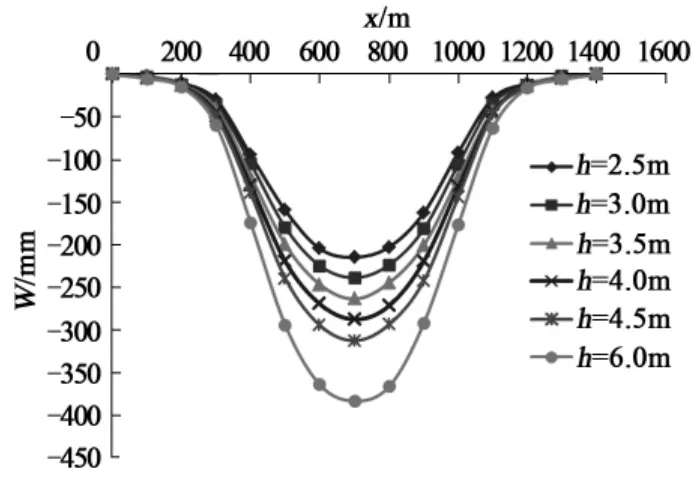
图7　不同采厚时结构关键层下沉变形曲线

(1)随着采厚的增加，在相同充填体密实度(η= 85%)的条件下，覆岩结构关键层的下沉量随之增加，覆岩结构关键层下沉量随采厚变化近似呈线性关系。

(2)当采厚由2.5m增加到6.0m时，覆岩结构关键层的下沉量由215mm增加到384mm，增加量仅为169mm。这表明:在控制覆岩结构关键层不破断的密实充填开采情况下，采厚对覆岩结构关键层变形的影响较小。

图8　结构关键层下沉量随采厚的变化曲线

2.2.3采深对覆岩变形的影响

图9给出了不同采深时覆岩结构关键层下沉变形曲线，图10给出了不同采深时覆岩结构关键层下沉量的变化曲线，可以看到:

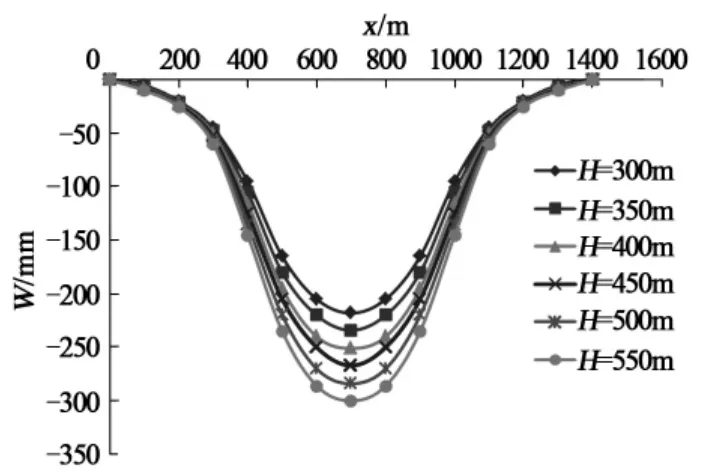
图9　不同采深时结构关键层的下沉变形曲线

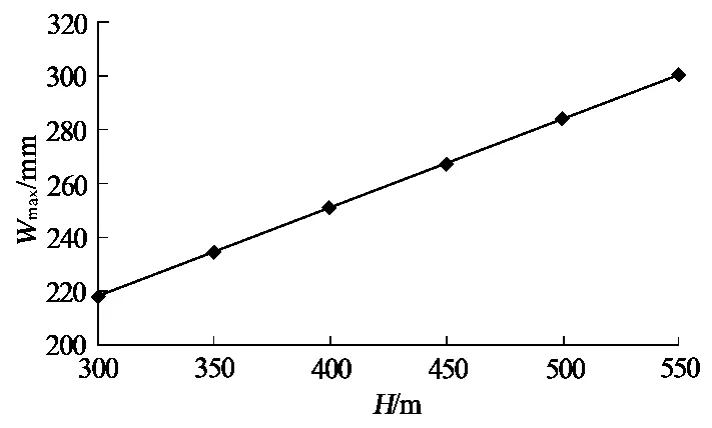
图10　结构关键层下沉量随采深的变化曲线

(1)随着采深的增加，在相同充填体密实度(η=85%)的条件下，覆岩结构关键层的下沉量随之增加，覆岩结构关键层下沉量随采厚变化近似呈线性关系。

(2)当采深由300m增加到550m时，覆岩结构关键层的下沉量由218mm增加到300mm，增加量仅为82mm。这表明:在控制覆岩结构关键层不破断的密实充填开采情况下，采深对覆岩结构关键层变形的影响较小。

3　结论

(1)建立综合机械化固体充填开采覆岩变形的对称层合板力学模型，在引入文克勒弹性地基的情况下，得到上覆岩层变形的控制微分方程，并提出相应的定解条件，计算得到上覆岩层变形的弹性解，通过算例分析，认为通过控制充填体密实度可以有效控制覆岩变形。

(2)数值计算表明，充填密实度对控制覆岩变形效果显著，当充填密实度η＜75%时，覆岩变形较大;当充填密实度η＞75%时，覆岩变形显著减小，结构关键层仅呈现较小的连续弯曲变形。同时，覆岩变形随采厚和采深呈线性变化，采厚和采深对覆岩变形影响较小。

(3)控制地表沉陷的关键在于控制覆岩结构关键层的变形，特别是控制覆岩结构关键层的破断。在工程实践中，可根据覆岩结构关键层随充填体密实度的变化规律，选取合适的充填方案，从而将覆岩变形及地表沉陷控制在许可的范围内。

［参考文献］

［1］缪协兴，张吉雄，郭广礼．综合机械化固体充填采煤方法与技术研究［J］．煤炭学报，2010，35 (1) : 1－6.

［2］钱鸣高．煤炭的科学开采［J］．煤炭学报，2010，35 (4) : 529－534.

［3］钱鸣高，缪协兴，许家林，等．论科学采矿［J］．采矿与安全工程学报，2008，25 (1) : 1－10.

［4］缪协兴．综合机械化固体充填采煤技术研究进展［J］．煤炭学报，2012，37 (8) : 1247－1255.

［5］张吉雄，缪协兴，郭广礼．矸石(固体废物)直接充填采煤技术发展现状［J］．采矿与安全工程学报，2009，26 (4) : 395－401.

［6］钱鸣高，许家林，缪协兴．煤矿绿色开采技术［J］．中国矿业大学学报，2003，32 (4) : 343－348.

［7］钱鸣高，缪协兴，许家林．资源与环境协调(绿色)开采［J］．煤炭学报，2007，32 (1) : 1－7.

［8］缪协兴，张吉雄，郭广礼．综合机械化固体废物充填采煤方法与技术［M］．徐州:中国矿业大学出版社，2010.

［9］钱鸣高，石平武．矿山压力与岩层控制［M］．徐州:中国矿业大学出版社，2003.

［10］缪协兴，张吉雄．矸石充填采煤中的矿压显现规律分析［J］．采矿与安全工程学报，2007，24 (4) : 379－382.

［11］缪协兴，黄艳利，巨峰，等．密实充填采煤的岩层移动理论研究［J］．中国矿业大学学报，2012，41 (6) : 863－867.

［12］张吉雄，李剑，安泰龙，等．矸石充填综采覆岩关键层变形特征研究［J］．煤炭学报，2010，35 (3) : 357－362.

［13］徐芝纶．弹性力学(下册)［M］．北京:高等教育出版社，2007.

［14］张吉雄．矸石直接充填综采岩层移动控制及其应用研究［D］．徐州:中国矿业大学，2008.

［15］马占国，浦海，张帆，等．煤矸石压实特性研究［J］．矿山压力与顶板管理，2003，6(1) : 95－96.

［责任编辑:王兴库］

矿山压力与灾害控制

Mechanics Analysis of Applying Solid Stowing to Controlling Surrounding Rock
Deformation with Full-mechanized Equipment

CAO Zheng-zheng1，2，JIANG Hai-lin2，HUANG Xiu-wen2，ZHOU Yue-jin1

(1.State Key Laboratory of Deep Rock and Soil Mechanics and Underground Engineering，China University of Mining＆Technology，Xuzhou，221116，China;
2.Mechanics＆Architecture Engineering School，China University of Mining＆Technology，Xuzhou，221116，China)

Abstract:By setting up symmetry laminate model of surrounding rock deformation in solid-stowing mining and presenting definite condition，analytical solution of surrounding rock deformation was obtained.Applying FLAC to building up numerical simulation of stowing mining model，the influence of stowing body＇s dense，mining height and mining depth on surrounding rock deformation was researched.Results showed that influence of mining height and depth on surrounding rock deformation took on linear relationship.The influence of stowing body＇s dense on surrounding rock deformation was more obvious.When dense η＜75%，deformation was large，and when it was minor than 75%，deformation largely reduced.Research result could provide reference for solid stowing mining theory and technique design.

Keywords:full-mechanized solid-stowing mining; surrounding rock deformation; symmetry laminate; FLAC

［作者简介］曹正正(1990－)，男，安徽砀山人，博士研究生，从事采动岩体力学与充填开采研究工作。

［基金项目］国家自然科学基金(51374201，51322401) ;国家重点基础研究发展计划(973)项目(2013CB227900) ;中国矿业大学校级大学生创新训练计划项目(X1029014017)

［DOI］10.13532/j.cnki.cn11－3677/td.2015.02.020

［收稿日期］2014－09－04

［中图分类号］TD325

［文献标识码］A

［文章编号］1006-6225 (2015) 02-0070-05