低应力水平下时间效应对岩石蠕变模型参数的影响
李成波
(安阳工学院 数理学院,河南 安阳 455000)
低应力水平下时间效应对岩石蠕变模型参数的影响
李成波
(安阳工学院 数理学院,河南 安阳 455000)
[摘要]在岩石蠕变实验数据基础上,通过拟合分析,得到了蠕变模型的相关参数。通过对比理论计算数据与实验数据,结果发现:不考虑参数受时间尺度的影响将引起较大的误差,对于蠕变模型来说,其参数不是常数,而是随时间变化的量,时间尺度对模型参数影响较为明显;如考虑参数的时间相关性,建立非定常参数的蠕变模型方程,将比定常蠕变模型更能准确地反映岩石的蠕变变形特征。
[关键词]蠕变实验; 蠕变模型;标准线性体;伯格斯;时间效应
1引言
为了预测岩石在应力长期作用下的变形规律,往往需要进行一系列蠕变实验,确定岩石的蠕变模型。一条完整的蠕变曲线通常分为:瞬态蠕变、稳态蠕变和加速蠕变等三个阶段[1]。在实验室中,对于低强度的岩石样品,稳态蠕变可以在中等应力水平下很快出现,而第三期蠕变很难出现,只有在高应力水平(大于80%时)下才有可能能够出现。所以在这里主要是针对前两阶段蠕变的研究,即低应力水平下的蠕变现象。
本文在蠕变实验结果的基础上,主要针对标准线性体模型和伯格斯模型之间的讨论比较,以及蠕变模型参数随时间效应的变化关系。通常的拟合计算中,所采用的蠕变模型参数大多认为是与时间无关的,称为定常参数模型。而实验表明,如果忽略时间效应的影响,两种模型都能很好地拟合数据。如果把实验数据分成不同的时间阶段,发现这些模型的参数都是与时间相关的,直接用这些固定参数来“预测”将来的蠕变趋势和蠕变值将存在较大偏差。而事实上,岩石在水和风化等因素作用下,其某些力学参数随时间的变化是明显的,比如岩体弹性模量和强度等参数随时间的增长而降低[2]等。
2蠕变实验
实验用的样品为采自郯庐断裂带附近的花岗岩、大理岩和砂岩3类岩石,加工成50×50×50 mm3大小。实验装置为全自动伺服液压试验机(YAW4605)系统,加有水冷设施,可保证压机系统连续稳定工作两个月。在样品表面对称贴有两组电阻应变片,与数字式应变仪(WS-3811)联接,采样频率为1Hz。用钢块对实验装置进行了的稳定性测试,应力和应变测量值是二条基本平行的直线,分别有±0.2MPa和±3微应变的波动。每次实验开始时,首先对样品迅速加压,让应力在几分钟内到达设定值,然后保持,应力可看成是阶跃函数。分别对不同类岩石在35、50和70MPa的应力下进行了蠕变实验,整个实验过程中,基本保持室温在±1℃的波动范围。图1中的实线为砂岩的蠕变实验曲线,该实验持续时间为20天。应变随应力达到设定值后上升到4830微应变,这一部分为弹性阶段。接下来让应力保持不变,而应变随时间继续缓慢增加,但其应变增长速率却在不断地减小。为了能够更好地突出蠕变变形部分,图中已经把弹性阶段的变形部分截去。图1仅为砂岩的蠕变曲线,其它种类岩石(大理岩、花岗岩)在不同应力下的蠕变曲线大致相近,限于篇幅没有一一列出。
Fig. 1The creep experiment curves of sandstone at 35MPa
3蠕变模型的比较与分析
在这里,仅将常用的标准线性体和伯格斯(Burgers)模型进行对比。
3.1 标准线性体模型
如图2(a)所示为标准线性固体模型,图中E1代表弹性元件的弹性系数,产生瞬时弹性应变。E2和η分别代表并联弹性元件的弹性系数和粘性元件(阻尼盘)的粘性系数,产生随时间变化的蠕变变形,该模型的本构方程[3]为:
(1)
式中ε为轴向应变,σ0为轴向应力,τ=η/E2为弛豫时间,t为实验持续时间,渐近模量Ef=E1·E2/(E1+E2)。从图1中可看出式(1)能够很好地模拟岩石在恒定应力作用下的蠕变特性,实测曲线和反演曲线的相关系数可达到0.99。式(1)也可以写成如下形式:
ε(t)=εf-εcexp(-t/τ)
(2)
式中,εf为渐进应变,εc为整个蠕变量。
当t=0 时,有初始的弹性应变ε0和模型的初始模量E0,由弹性模量E1决定,且E0=E1。当t趋于无穷时有渐近应变εf和蠕变量εc=εf-ε0,模型的渐近模量Ef=(E1·E2)/(E1+E2),且可推导得出E1/E2=εc/ε0,定义模量比值为:C=E2/E1。
Fig. 2 (a)standard linear model and (b) Burgers model
3.2 伯格斯模型(Burgers)
Burgers模型是Kelvin模型和Maxwell模型的串联体,如图2(b)所示。模型的四个参数: GK和GM,ηK和ηM分别为Kelvin和Maxwell模型的弹性模量和粘滞系数。蠕变方程为[4]:
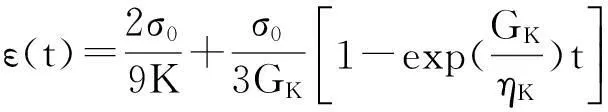
(3)
式中ε为轴向应变,t为时间,K为体积模量,σ0为恒定应力。
由于在轴向应力条件下,σ2=σ3=0,所以偏向应力σ1,dev=2σ1/3,偏向应变ε1,dev=ε1-εm,这里的εm为平均应变值。假设泊松比=0.25,有σm=3Kεm,ε1=σ1,devG /2+σmK /3,σm为平均应力值。
标准线性体模型主要是描述暂态蠕变的。标准线性体表现为固体,其中的阻尼器单元是固体的滞弹性,该阻尼器单元与并联弹簧单元一起,表征了弛豫时间的长短。而伯格斯模型包含了稳态蠕变阶段,能够求出稳态变形时的粘滞系数。如果实验时间不是太长,有可能只观测到暂态蠕变部分;如果实验时间足够长,往往也能够观测到稳态蠕变部分,所以选择这两个代表性的蠕变模型作为理论依据。
4非定常蠕变模型
4.1 时间尺度对模型参数的影响
为了进一步寻找蠕变模型参数受时间尺度的影响规律,做如下分析。对实验所得数据进行了分段处理,即假定实验分别在5天、10天、15天和20天的时间结束。假定蠕变实验在5天时结束,所得模型的参数分别代入蠕变方程(1)和(3),然后再将时间外延到20天,就得到每个模型对应的预测应变曲线,如图1虚线所示。图1箭头所示的右半部分, 是模型在5天~20天预测曲线,与实验曲线比较有明显的偏离。伯格斯模型预测值偏大,而标准线性体模型预测值偏低。分段的实验数据都用两种模型来反演,所得的各参数值见表1。表1中所有参数计算的理论值与实测数据的相关系数都在0.99以上,说明无论实验时间多长,这两个模型都可以很好地拟合实验数据,但对后面的“预测”这一标准而言,模型都不是合适的模型,即模型的预测曲线,与实测曲线都有明显偏离。如果假定实验在10天时结束,也得到相似的结果。

表1 对实测数据分段反演蠕变模型所得的参数(应力水平为0.21)
为了更进一步了解时间尺度对蠕变模型的影响,选用更为大的时间尺度进行分析。引用文献[5]中的数据,该数据所测试样为边长5cm的立方体,岩性为具有一定胶结的断层岩(大理岩区),岩石强度为2MPa,结构比较均匀,实验在轴向应力条件下持续了近80天,应力水平为0.14,也进行了类似的反演计算,计算结果见表2。
对实验数据分几个不同时间尺度来反演并绘出理论曲线,再和实测曲线作比较,目的是为了说明各个模型在不同时间尺度上和实际情况的吻合程度。每个模型都可用于岩石蠕变数据的模拟,拟合用到数据的时间范围越长模拟的结果越和实际相吻合,参数也接近实际情况。从表1和表2可以看出,在两个模型中,除弹性元件参数E1、K和GM外,其他参数都随实验时间变化而变化,三个模型的参数都是和时间相关的。不管应力水平为多少,或者实验持续时间的长短,同样存在着模型参数随时间有规律地变化,对于标准线性体来说,模型的参数呈现明显的规律,驰豫时间越来越长,C值越来越小。
4.2 非定常蠕变模型
由实验数据可以拟合计算出全部模型参数,如弹性模量E1和E2,渐近模量Ef和渐近应变εf,最大蠕变量εc等,所得参数都是固定的。而从表1和表2的结果可见,不同时间尺度的实验计算出的参数不尽相同,并且它们都是和时间相关的。如在标准线性体模型的计算中,时间越长,则弛豫时间也变长,渐近应变εf不断增加,相应的蠕变量εc也逐渐变大,但弹性模量E2却变小,称为模量亏损。针对实验数据的拟合计算具有模型和参数的不唯一性特点。
为了取得较好的计算模拟效果,提出了变参数的标准线性体模型,即非定常蠕变模型。假设模量比和粘滞系数都是随时间变化的,可表示为C(t)=E2/E1和η(t),根据不同实验时间分段计算,得其规律性:C(t)=6.389+13.57×exp(-t/528219)和η(t)=4.289+1.205×10-6t (1016Pa·s),代入式(1)中,修正前后的理论曲线见图3和图4。图中Ⅰ区为用于反演计算的实测数据段,Ⅱ区为用于将理论预测曲线和实测曲线比较的数据段。可以看出修正后的标准线性体模型比原来未修正之前的预测能力有了很大提高。对于80天的断层岩实验,也能用相同的方法进行处理提高标准线性体的预测能力,图4所示,它在第Ⅰ和第Ⅱ阶段与实验曲线符合较好,满足模型判断标准。
5结论
各种岩石的蠕变特征,主要由岩石蠕变曲线来体现。对实验数据分不同时间尺度来反演并绘出理论曲线,再和实测曲线作比较,目的是为了说明各个模型在不同时间尺度上和实际情况的吻合程度。结果表明,两种模型都可用于岩石蠕变数据的模拟,拟合用到数据的时间范围越长模拟的结果越和实际相吻合,参数也接近实际情况。但把实验数据分成不同的阶段时,蠕变模型的参数都在随时间变化。不考虑参数的时间相关性,其计算值与实测值相差较大,尤其是应力水平较大时,这种误差更大。
由于实验室中的蠕变实验的持续时间远比实际环境下岩体的蠕变时间尺度小很多,直接从实验结果外推的话势必将导致一系列偏差。如果在蠕变模型中引入非定常参数,可以减小理论计算值与实测值的差异,吻合较好。这种将岩石蠕变力学参数看作是非定常的,将会更加直接而客观地反映岩石的非线性黏性时效特征。采用非定常的非线性蠕变模型代替传统上定常的线性蠕变模型将能以更加准确地预测岩石的时效非线性变形特征,它将是下一步深化研究的一个努力方向[6]。这种变化一直持续到更大时间尺度上,如地震后的形变和冰后期的地面回升。如果时间效应机制能够明确或是有规律变化被发现,对蠕变速率和软流层粘滞系数的估计将会很大程度的提高。目前,从可用的数据来总结,这一机制还没有很清楚的认识,还有待进一步研究。
[参考文献]
[1]Boukharov G.N., Chanda M.W., Boukharov N.G.. The three processes of brittle crystalline rock creep[J]. International journal of rock mechanics and mining sciences, 1995, 32(4):325-335.
[2]吕爱钟, 丁志坤, 焦春茂, 等. 岩石非定常蠕变模型辨识[J]. 岩石力学与工程学报, 2008, 27(1):16-21.
[3]尹祥础. 固体力学[M]. 北京: 地震出版社. 1985.
[4]沈振中, 徐志英. 三峡大坝地基花岗岩蠕变实验研究[J]. 河海大学学报, 1997, 25(2):1-7.
[5]邓荣贵, 周德培, 张倬元, 等. 一种新的岩石流变模型[J]. 岩石力学与工程学报, 2001, 20(6):780-784.
[6]孙钧. 岩石流变力学及其工程应用研究的若干进展[J]. 岩石力学与工程学报, 2007, 26(6):1081-1106.
[责任编辑:D]
[中图分类号]TU 45
[文献标识码]A
[文章编号]1671-5330(2015)02-0010-04
[作者简介]李成波(1980—),男,安阳人,讲师,博士,主要从事岩石物理实验方面的研究。
[收稿日期]2015-02-20

