基于SIMPLE算法的大型浮顶油罐温度场数值模拟
张 琰 ,白 云 ,王常莲 ,陆翌伦
1.中国石油大学(北京) (北京 102249)
2.北京化工大学 (北京 100029)
3.中国石油天然气股份有限公司规划总院 (北京 100083)
4.北京市二十一世纪国际学校 (北京 100142)
油罐是原油储备库的主要储存设备,其建设投资和生产过程中的能耗费用均在总费用中占很大比例。浮顶油罐建设大型化是当今油库建设的主要趋势,因其具有单位罐容耗钢量小、相对能耗小、总占地面积较省和管理方便等优点[1-3]。
原油储运在生产运行过程中,由于原油与周围环境存在温差,会通过罐顶、罐壁和罐底土壤进行热交换。若罐内原油降到凝点以下,罐内部分原油发生凝固,即在浮顶、罐壁和罐底内沿处形成一定厚度和强度的凝油。凝油可能阻塞油罐出油管,导致事故发生;在油罐恢复作业时,这些凝油尤其是罐顶的凝油会威胁大型浮顶罐的安全启动[4-5]。为了防止罐内原油的凝固,需要对罐内原油适时进行加热或者倒罐。加热周期太短,会浪费大量能源;加热周期太长又可能会导致凝油危险。为了经济合理地运行油库加热系统,科学确定加热或倒罐周期,必须掌握罐内原油的温度场变化规律[6]。因此,为了得到油罐内原油冷却到凝点的时间以及冷却过程中原油的运动情况,需要对罐内原油冷却过程中的温度场进行模拟。
1 数学模型建立
1.1 控制方程
流体的流动与传热过程都遵守质量守恒定律、动量守恒定律和能量守恒定律。针对大型浮顶油罐的特性,在柱坐标下建立控制方程。柱坐标下的控制方程如下:


式中:u,v为 x,r方向上的无量纲速度;p为无量纲压力;ρ为无量纲密度;t为无量纲时间;T为无量纲温度;Pr为普朗特数;ψ为流函数;η为扩散系数;φ为通用变量,可以代表u,v,T等求解变量;Γφ为广义扩散系数;Sφ为广义源项。
1.2 封闭方程的条件和定解条件
大型浮顶油罐中的自然对流处于低速范围内,且能够忽略流体的压缩性,故本研究利用粘性不可压缩流体运动的封闭方程组[7-9]。为使控制方程在封闭条件下能够得出确定的解,还必须要有合适的定解条件,即初始条件和边界条件。研究中罐壁处的速度边界采用无滑移条件,罐顶和罐壁处采用第三类边界条件。
1.3 计算区域和控制方程的离散
本问题属于压力、速度耦合数值求解,故在交错网格中对动量方程进行离散。在离散时,速度项采用一阶迎风格式,压力项采用向前差分格式,扩散项采用中心差分格式,具体离散结果见式(6):

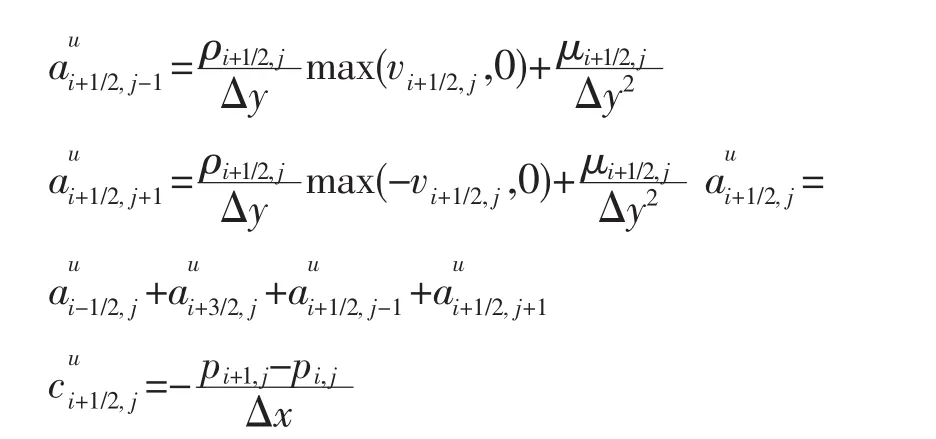
动量方程y方向的离散形式与上面相同,此处不再叙述。
1.4 SIMPLE算法
SIMPLE算法就是求解压力耦合方程的半隐方法,此算法的压力修正基本思想如下:在迭代某一层次上,可以给定一个压力场,他可以是假定的或者是上一层次计算得到的,但是这样的压力场不能满足连续性方程,需要对压力场进行修正,但是必须使改进后的压力场所对应的速度场能够满足这一层次的连续性方程[10]。
利用SIMPLE算法继续将式(6)离散,在某个迭代层次,压力为pˆ,根据此压力值从动量方程中得到预估的速度,根据连续性方程对压力与速度进行修正(上标为“’”的为修正项),使其同时满足这一轮次上的动量方程和连续性方程。设修正后的压力值p为:

需要注意的是,在求解压力修正方程时,将压力值代入方程得到修正后的压力和速度值,压力修正方程式中,忽略了邻点速度的修正值,因此需对压力项进行亚松弛处理。
2 数值模拟计算
2.1 建立模型
由于大型浮顶油罐尺寸较大,故选取油罐纵断面的一半为研究对象,将三维问题转化为二维旋转轴问题。模型的最上方为浮顶区,忽略浮仓内隔板的影响,将浮仓简化为1m的空气层;中间部分为原油区,储罐半径设置为40m;下方为土壤区,将其视为半无限大的均匀介质,厚度10m;罐壁保温层厚度80mm。以油高18m的储罐为例,模型如图1所示。
为便于模型的求解,将基本条件作如下简化:
1)整个油品区域在初始时刻的温度为恒定值,本文取298K。
3)因此,输入序列x(n)可以表示为单位抽样序列δ(n)的移位相加;输出序列y(n)可以表示为单位脉冲响应序列h(n)的移位相加。相对于输出序列的卷积表达式而言,输入序列的卷积表达示中,由于单位抽样序列仅在零点有值,因此序列翻转前后没有变化,相乘运算只是乘以1个采样点的值,且幅度为1,因此相当于没有翻转和相乘的运算步骤。
2)忽略辐射换热,只考虑导热和自然对流。
3)设土壤、保温层、空气等物性均匀,它们的热容及导热系数为常数,相关物性参数见表1。
4)假设在距地表以下10m埋深处地温恒定,本文为10℃。
5)设大气温度每天变化相同,每天大气温度随时间变化的函数为:
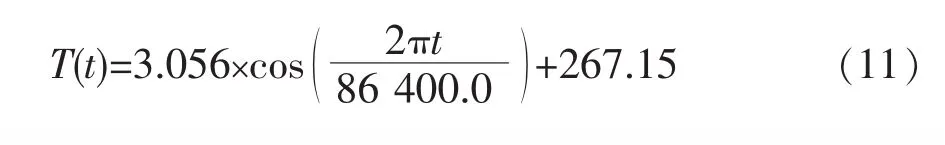

图1 大型浮顶油罐数学模型

表1 相关物性参数表
2.2 网格划分
所建模型属于旋转轴问题,在Gambit划分网格时,必须以x轴方向为旋转轴,故需将模型旋转90°。温度变化较剧烈处进行网格加密,相邻网格宽度之比应该接近1,文献推荐相邻网格宽度之比宜保持在0.8到1.2之间[9]。储罐及周围土壤的模型网格划分如图2所示,其中红色为土壤区,蓝色为原油区,绿色为空气区。

图2 模型的计算网格
2.3 前处理及计算求解
计算了外界环境温度周期性变化时,油高为10m的储罐在10天内的温度场变化分布;为研究油罐内液面高度变化对储罐内原油温度场的影响,该研究选取18m、10m和5m作对比算例;为研究浮顶加盖保温层对储罐内原油温降的影响,计算了油高为10m的浮顶加盖保温层的储罐10天内的温降变化。
2.4 计算结果合理性分析
由于油库单位不可能测量罐内每处的温降,现仅有若干天的平均温降数据,其中秦皇岛油库、冀东油库、鄯善油库的储罐温降在0.2~0.4℃/d,研究中18m、10m和5m液高的储罐温降分别为0.34℃/d、0.25℃/d和0.22℃/d,符合工程实际情况,故表明计算数据比较可靠。
3 影响储罐原油温度场因素分析
3.1 储罐内原油随时间的变化
为探讨储罐内原油随时间的变化,计算了外界环境温度周期性变化时,原油高度为10m的储罐在10天内的温度场变化分布。图3~图6为储罐的原油部分在第1、3、5和10天后的温度场分布(为使图例直观,适当调节了温度标尺)。
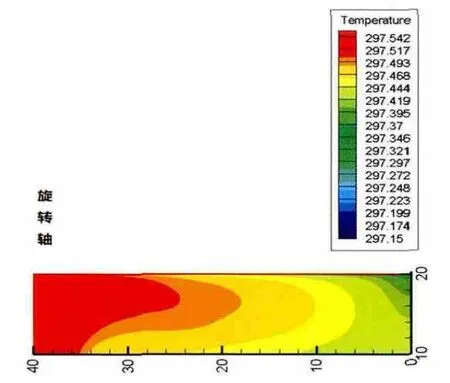
图3 油罐静置1天后温度场分布
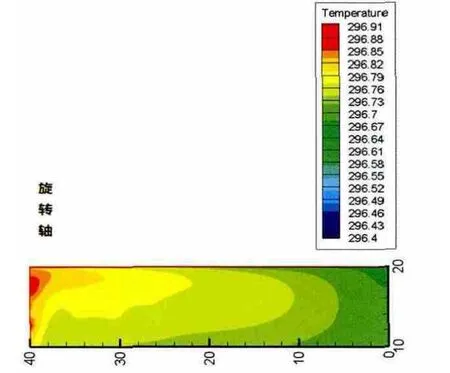
图4 油罐静置3天后温度场分布
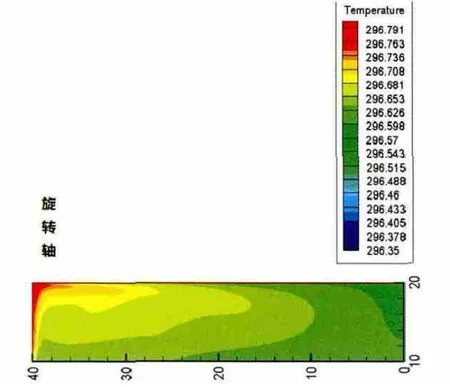
图5 油罐静置5天后温度场分布
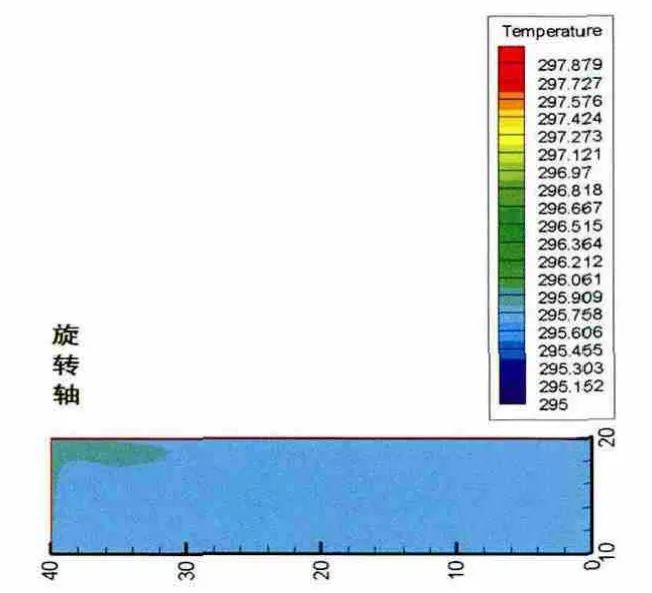
图6 油罐静置10天后温度场分布
大型浮顶油罐随时间的平均温降如图7所示,可见初期温降速率较大,随时间的增长温降速率逐渐降低。故初期将罐内原油加热到很高的温度并不能有效地延长原油的加热周期,反而使热量损耗变大,增加运营成本。
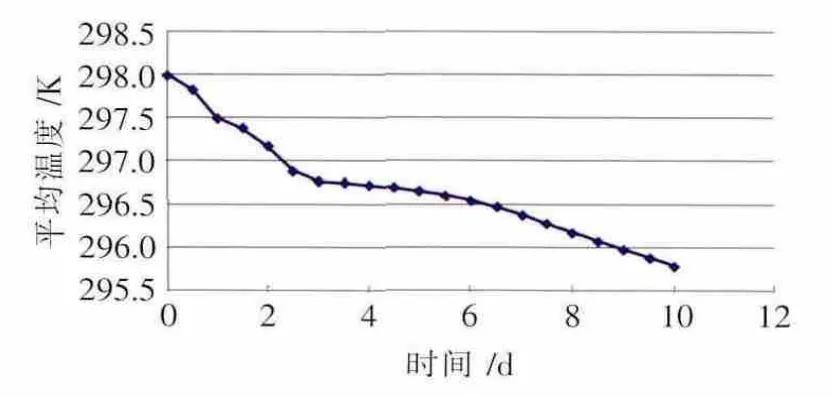
图7 储罐液高10m时原油平均温度变化
3.2 储罐存油量对温降的影响
选取储罐原油液位为18m、10m和5m为研究对象,计算出3种情况下原油在10天后的平均温度以及温度场分布。其中大型浮顶储罐原油液位为18m时,在静置10天后的平均温降为0.22℃/d;液位为10m的平均温降为0.25℃/d;液位为5m的平均温降为0.34℃/d。故储罐内原油的液位越高,储罐内原油的温降速率越低。其中2种液位的储罐在10天后的温度场分布如图8~图9所示。
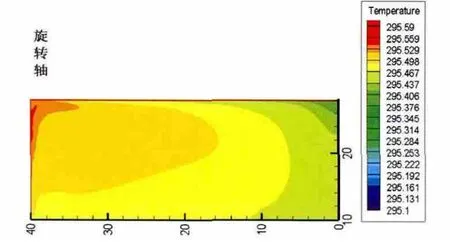
图8 18m液高10天后温度场分布
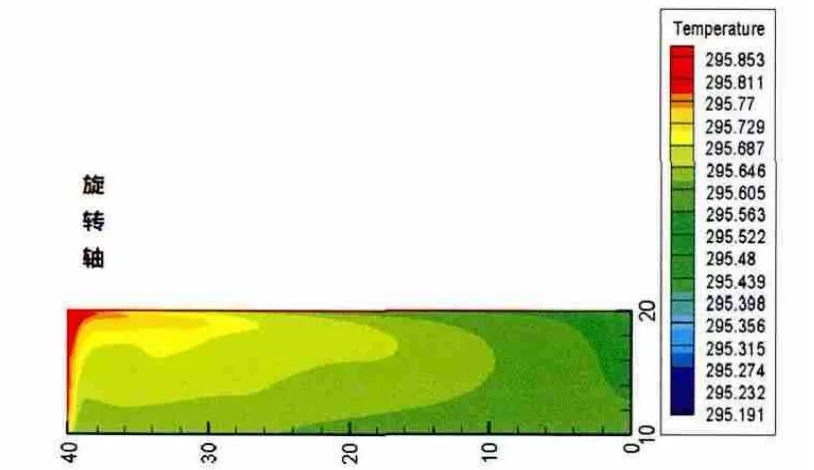
图9 10m液高10天后温度场分布
3.3 储罐浮顶是否加盖保温层的探讨
当前我国许多大型浮顶油罐罐顶没有加盖保温层,仅靠双盘之间的空气层保温,为讨论罐顶加盖保温层是否具有明显的保温效果,计算了罐顶加盖保温层的储罐在液高10m时的温降特点,其10天后的温度场如图10和图11所示。
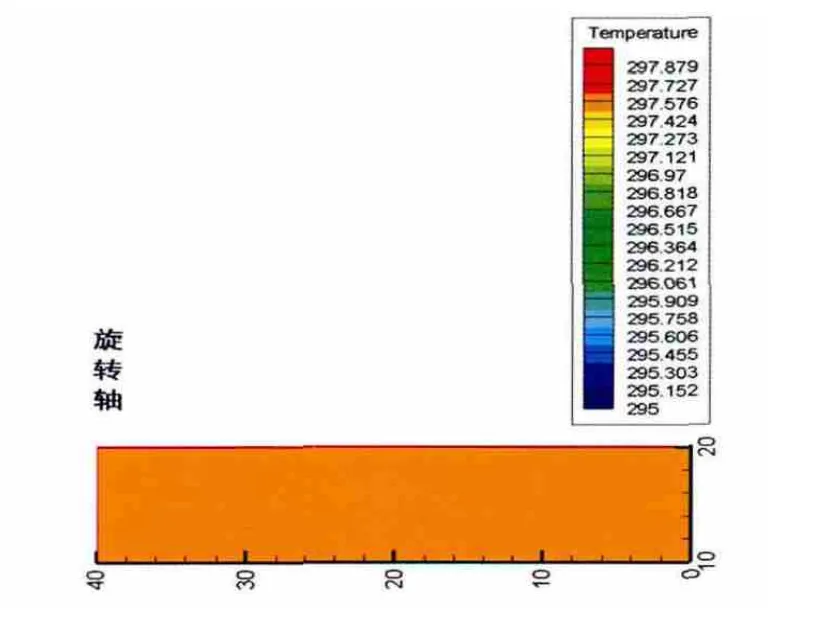
图10 罐顶加盖保温层
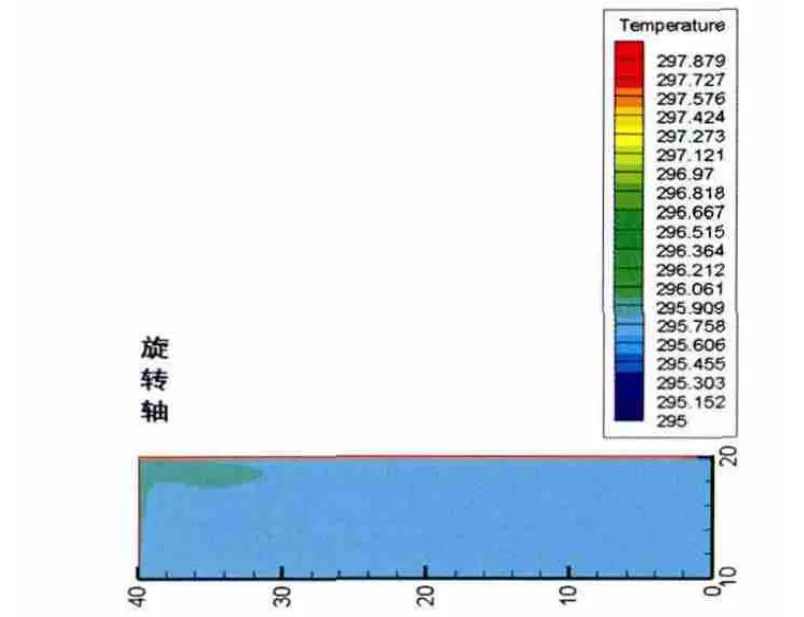
图11 罐顶没有保温层
大型浮顶油罐罐顶加盖保温层后,平均温降为0.07℃/d,与罐顶没有加盖保温层时的0.25℃/d相比,温降速率降低72%。所以罐顶敷设保温层具有良好的保温效果,但是罐顶保温层一旦受到破坏,水和原油进入保温层后,使其变成一层“湿棉被”,其保温效果大打折扣,甚至不如罐顶不敷设保温层。
4 结论
1)浮顶罐的热量主要从罐顶和罐壁散去。靠近储罐中轴线的上方部分原油温度较高,而靠近罐壁上层的原油是罐内温度最低的。
2)大型浮顶油罐内原油前3天的温度降低速率较快,但随着时间的推进,温降速率逐渐减低。
3)储罐内原油的液位越高,罐内原油的温降速率越低。
4)较罐顶没有保温层的储罐相比,罐顶加盖保温层具有较强的保温效果,在保温层良好的情况下,温降速率可降低70%左右。
5)通过与秦皇岛油库、冀东油库和鄯善油库的储罐温降范围对比,表明计算数据可靠,对储罐的建设及运营有一定的借鉴意义。

[1]刘晓山,邱宏宇,张斌.150000m3浮顶油罐国产化设计展望[J].压力容器,2004,21(5):32-35,44.
[2]于达.大型浮顶油罐测温系统的研发[J].油气储运,2005,24(8):41-43.
[3]于达,方徐应,李东风,等.大型浮顶罐储油温降特点[J].油气储运,2003,22(9):47-49.
[4]朱作京,于达,宫敬.储油罐温度场模拟过程中传热相似理论[J].油气储运,2007,26(12):37-42.
[5]李超,李旺,刘人玮,等.大型油罐加热技术及温度场研究现状与展望[J].油气储运,2013,32(11):61-66.
[6]侯磊,白宇恒,黄维秋.浮顶罐内原油温降计算方法研究[J].科技通报,2010,26(1):159-164.
[7]Masoud Rahimi,Arsalan Parvareh.CFD study on mixing by coupled jet-impeller mixers in a large crude oil storage tank[J].Computers and Chemical Engineering,2007(31):737-744.
[8]张宁,李光正.特殊条件下矩形封闭空腔内自然对流数值研究[J].华中科技大学学报:自然科学版,2002,30(7):95-97.
[9]李旺,王情愿,李瑞龙,等.大型浮顶油罐温度场数值模拟[J].化工学报,2011,62(S1):108-112.
[10]陶文铨.数值传热学[M].西安:西安交通大学出版社,2001.

