一种基于平面波静态编码的最小二乘逆时偏移方法

黄建平， 李闯*， 李庆洋， 郭书娟， 段心彪， 李继光， 赵胜天， 步长城

1 中国石油大学(华东)地球物理系， 青岛 266580 2 中国石化南京物探研究院， 南京 210000 3 胜利油田物探研究院， 山东东营 257000



一种基于平面波静态编码的最小二乘逆时偏移方法

黄建平1， 李闯1*， 李庆洋1， 郭书娟2， 段心彪2， 李继光3， 赵胜天3， 步长城3

1 中国石油大学(华东)地球物理系， 青岛 266580 2 中国石化南京物探研究院， 南京 210000 3 胜利油田物探研究院， 山东东营 257000

平面波偏移是一种面炮偏移方法，相对于常规逐炮偏移，其具有较高的计算效率.然而常规平面波偏移方法成像精度低，且成像时会产生串扰噪音.为此，本文在实现常规平面波偏移算法基础上，引入反演思想实现了基于静态平面波编码的最小二乘偏移理论方法及处理流程，在优化算法基础上对平层模型和复杂砂砾断块模型进行了成像测试并与其他成像策略进行对比.研究结果表明：基于时移编码的平面波最小二乘偏移能有效抑制低频成像噪音和串扰噪音，补偿中深部成像能量，是一种较为有效的保幅成像策略.

平面波偏移； 岩性成像； 平面波编码； 最小二乘偏移； 保幅成像

1 引言

近年来，油田勘探开发已进入中、晚期阶段，为了满足目前油田开发的需要，小面元、高覆盖次数的高密度地震采集方法开始得到关注，特别是在国外海上勘探区块，已经普遍推广应用高密度空间采样技术(夏颖等，2008；赵会欣等，2008).高密度采集得到的海量数据符合平面波偏移对覆盖次数的要求，同时其计算效率问题也能通过面炮合成压缩炮记录解决( Berkhout, 1992).另一方面，目前地震勘探成像研究逐渐步入精细成像阶段，常规叠前深度偏移已不能满足构造成像向岩性成像过渡的需求，而基于反演思想的最小二乘偏移是高精度保幅成像的有效方法，但存在计算效率低的缺陷.因此，基于平面波编码加速的最小二乘偏移方法具有一定的研究意义.

“面炮”偏移首先由Berkhout(1992)提出, 通过某种合成算子将所有的炮道集合成为一个面炮记录,然后采用适于常规炮集的偏移算法进行偏移.Monsher等(1997)提出应用Randon变换的偏移距道集数据平面波偏移.随后，张叔伦和孙沛勇(1999)将面炮技术应用于傅里叶有限差分叠前深度偏移,提高了波动方程叠前深度偏移的计算效率.陈生昌等(2002)、冯伟等(2004)通过平面波合成算子合成不同角度的平面波记录，一系列方向的平面波偏移结果相叠加,进而得到较高精度的地下复杂介质的图像.为了进一步提高计算效率，孙沛勇和张叔伦(2000)提出了最大能量震源波场的平面波叠前深度偏移方法.此外，叶月明等(2007)、杨海生等(2011)将平面波偏移用于起伏地表的情况.

近年来，最小二乘算法在地震资料处理解释方面发挥了越来越重要的作用，其思想由LeBras和Beudoun(1988)等人提出，Lambare等(1992)在他们研究基础上，使用最速下降法(王彦飞，2007)反演相对于背景速度的速度扰动.Nemeth等(1999)早期将最小二乘算法引入到地震偏移以求取地下反射系数，他通过Kirchhoff最小二乘偏移方法对不完整的反射地震数据进行成像.此外，黄建平等(2013a)也应用Kirchhoff最小二乘偏移对我国西部探区碳酸盐岩裂缝型储层进行成像研究，刘玉金等(2013)应用Kirchhoff最小二乘偏移解决了地震数据中采样不规则、地震道缺失对成像造成的影响.随后，Kuehl和Sachhi (2001, 2003)和黄建平等(2014b)将Stoffa等(1990)提出的裂步算子应用到最小二乘偏移，贾晓峰和胡天跃(2005)也提出采用滑动最小二乘窗求解波动方程.黄建平等(2014c)将分频编码应用于最小二乘裂步法偏移，在提高计算效率的同时压制了串扰噪音.为了增加最小二乘偏移方法对剧烈横向变速的适应性，杨其强和张叔伦(2008)、黄建平等(2013b)实现了基于最小二乘的叠前深度偏移算法.近年来，国内外研究学者也将逆时偏移算子应用到最小二乘偏移中来进行复杂构造的保幅成像处理(Dai and Schuster, 2009, 2013; Dai et al., 2010, 2011, 2012; Li et al, 2014, 黄建平等, 2014a；郭振波和李振春, 2014).

本文在前人工作的基础上实现了基于静态平面波编码的最小二乘逆时偏移方法.为了加快收敛速度，本文加入了基于照明补偿预条件算子，并混合使用共轭梯度法与最速下降法进行寻优.通过成像测试深入分析了该方法在保幅性、成像分辨率以及横向能量均衡性等方面的优势，解决了常规成像时的复杂小断块边界难以分辨的问题，有利于后期断块油气藏的储层划分及油藏描述工作.

2 平面波最小二乘偏移方法原理

2.1 观测记录的平面波编码

对于一个二维工区，对炮记录编码的过程可表示为

(1)

其中，d(xg,t;xs)为观测炮记录，δ(t-pxs)为编码函数，编码过程等价于通过tau-p变换合成平面波记录，图1为平面波编码的原理图(Zhangetal., 2005)，时移量pxs随震源点位置xs线性变化，p为射线参数，

(2)

其中,θ是地表入射角，v是地表速度.

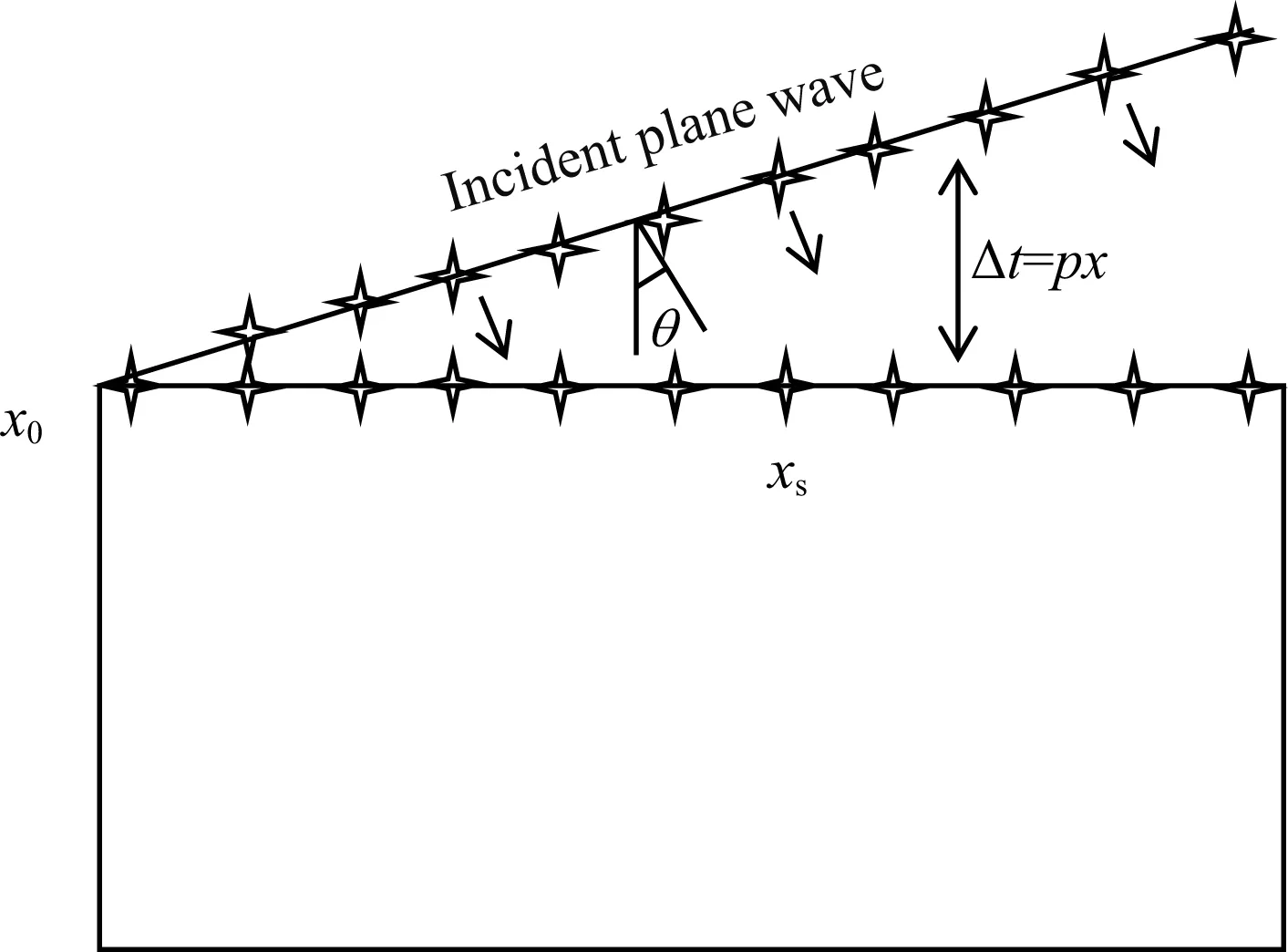
图1 平面波编码示意图(Zhang et al.，2005)Fig.1 Diagram of plane-wave encoding

2.2 震源的平面波编码

逆时偏移时需要进行震源波场的正向延拓，同样地，对第i个震源的编码过程可表示为

(3)

其中，s(t)为震源函数，wi(p,t)为时移后的震源，该过程相当于对各炮点进行一次与其位置有关的时移，注意对炮记录和震源的编码是一一对应的.编码完成后，激发平面波震源，模拟得到正向延拓的震源波场.

平面波记录的逆时偏移算子和炮域逆时偏移(Baysaletal., 1983)相同，由反传的合成平面波记录和平面波震源激发得到的震源波场相关成像.

2.3 平面波域反偏移算子

反偏移时仍然要对震源进行平面波编码，假设W(p,ω)为按式(3)编码后的平面波震源，给定一个背景慢度场s0，亥姆霍兹方程的解可表示为

(4)

其中，G0(x;xp)为背景慢度s0对应的格林函数，U0(p,x)为该平面波震源对应的波场，xp对应不同参数p的平面波震源.

假设慢度扰动为δs(x)，真实速度场可表示为s(x)=s0+δs(x)，求解Helmholtz方程可求得全波场：

(5)

震源项为F(p,x,ω)=-δ(x-xp)W(p,ω)，将s(x)=s0+δs(x)代入(5)式，并舍去高阶项O(δs2)得

(6)

将方程(6)的第三项移到右边，两边同乘以格林函数G0(x;x′)，再在整个介质中积分可得：

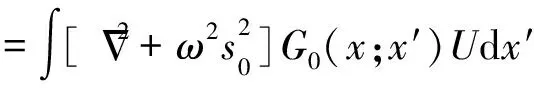
=-∫Uδ(x-x′)dx′

=U(x)

右边 = ∫G0(x;x′)Fdx′-2ω2∫s0δs(x′)U(x′;xp)

×G0(x;x′)dx′

=U0(x)+ω2∫m(x′)U(x′;xp)G0(x;x′)dx′,

(7)

其中，m(x′)=-2s0δs(x′)代表反射率.而全波场U(x′;xp)=W(p,ω)G(x′;xp)，假设慢度扰动足够小，即G(x′;xp)≈G0(x′;xp)，则Born近似下的散射波场为

U1(p,x) =U(p,x)-U0(p,x)

≈ω2∫m(x′)W(p,ω)G0(x′;xp)G0(x;x′)dx′.

(8)

为了简化公式，用矢量矩阵符号来表示Born正传算子：

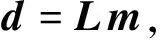
(9)

其中，m为偏移剖面或反射系数的矩阵形式；d是反偏移得到的平面波记录的矩阵形式；L为Born近似下的平面波域反偏移算子矩阵形式.

2.4 预条件算子

为了更好地补偿深部照明的不足，本文使用一种照明算子进行补偿(Beydoun and Mendes, 1989; Luo and Schuster, 1991)，该算子可表达为

(10)

其中，U(p;x,z;t)为射线参数为p时、t时刻的震源波场，I(p,x,z)为射线参数为p的平面波记录的照明算子.

2.5 平面波最小二乘逆时偏移

假设有Np个平面波道集，平面波域的误差函数可表示为

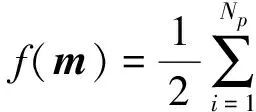
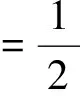
(11)

其中，di代表第i个平面波道集，而Li是与该平面波道集有关的正演算子，mi是与第i个平面波道集有关的偏移剖面.本文使用共轭梯度法求解平面波域的误差函数：

(12)

其中，I即为2.4节讨论的照明补偿预条件算子.

当目标函数为n维的二次可微函数时,利用共轭梯度法理论上最多只要n次迭代即可达到极小值点，但在实际计算中存在舍入误差、计算误差等因素，n次迭代后往往不能收敛，而n维函数问题的共轭方向最多只有n个，所以n次以后的迭代将失去意义，同时误差的积累会对收敛不利(陈开周，1985).因而，本文使用的共轭梯度法会在n次迭代之后将方向重设为最速下降方向重新启动算法.本文所使用的共轭梯度法的流程为：

(1)令迭代步数k=0，k1=0,设定允许误差ε和一轮搜索的最大次数n，初始搜索方向为最速下降方向；

(2)计算最速下降方向g(k)，若‖g(k)‖≤ε，则停止迭代，输出当前模型m(k)；

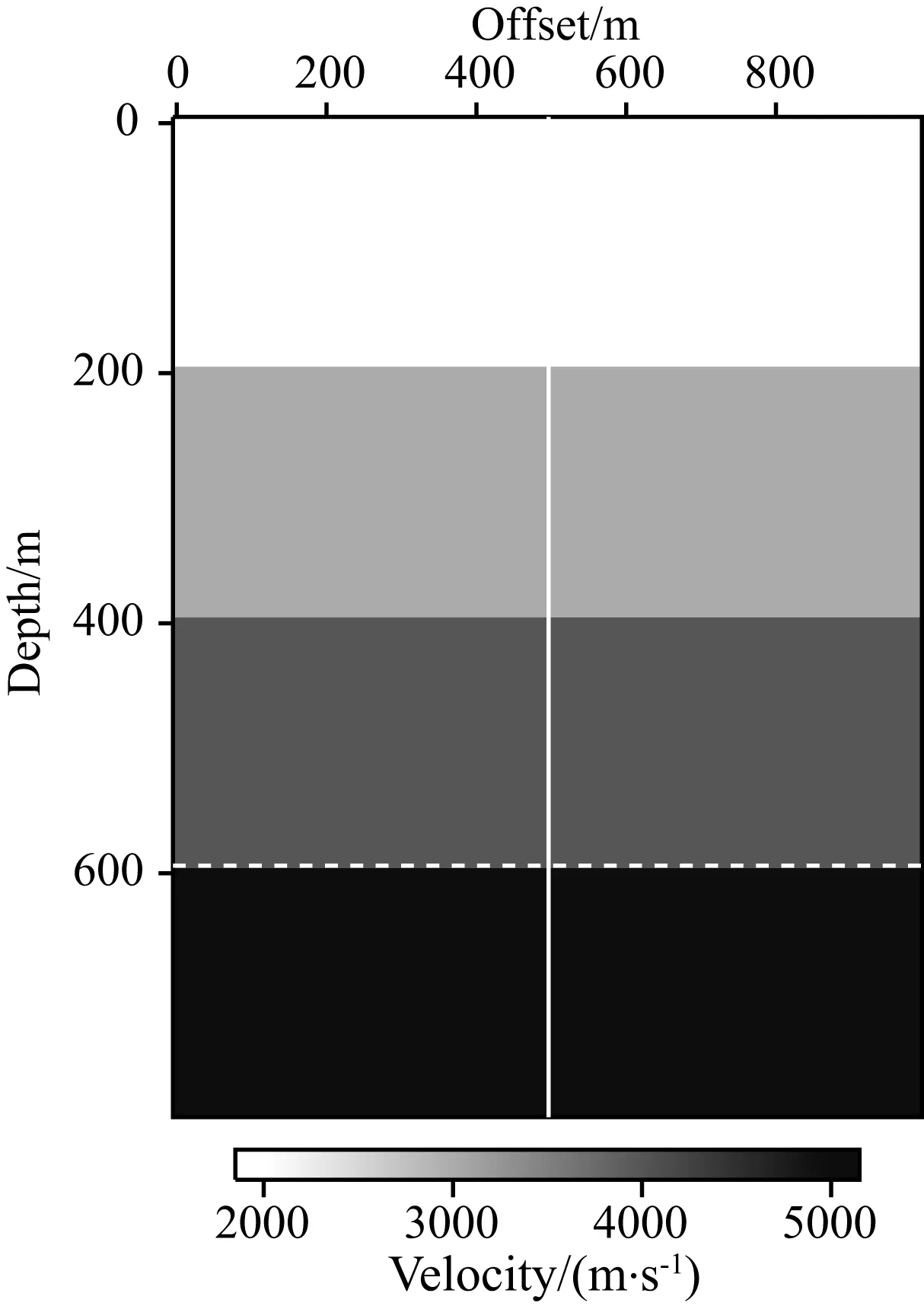
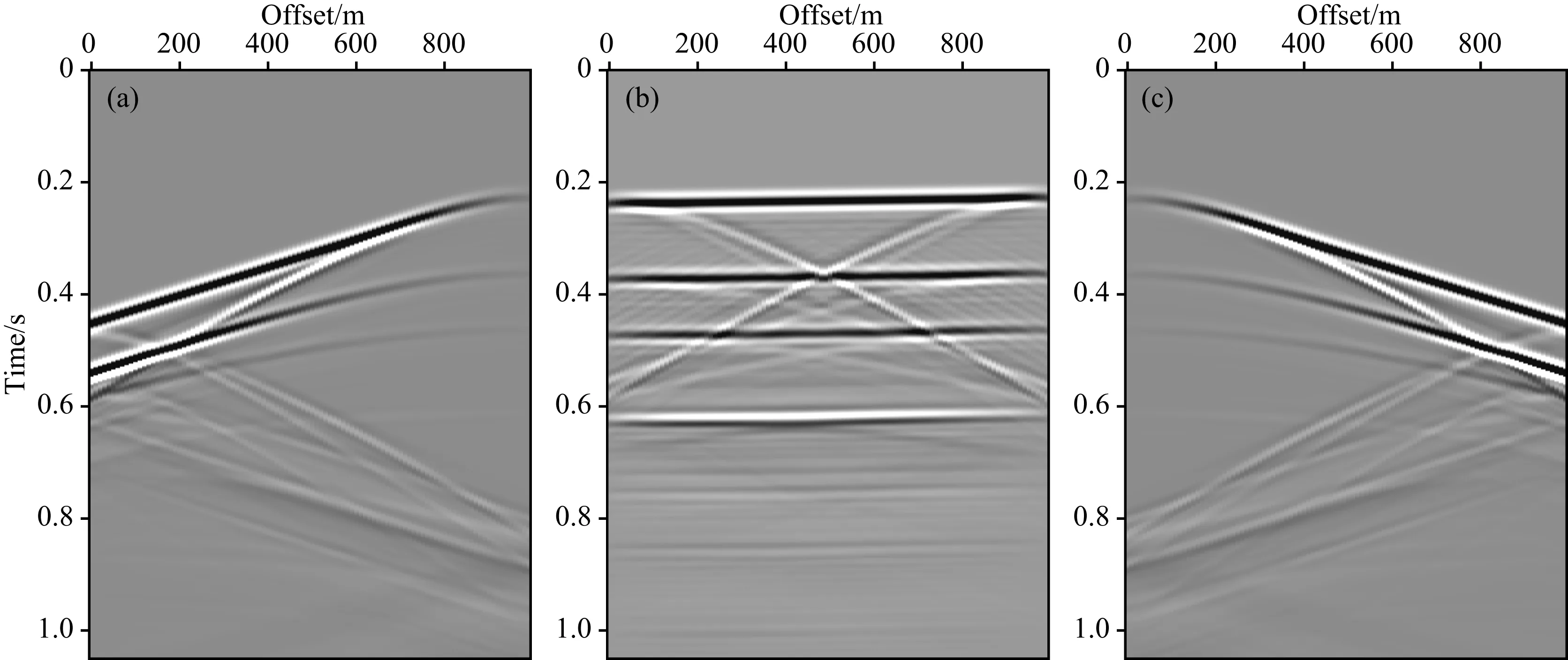
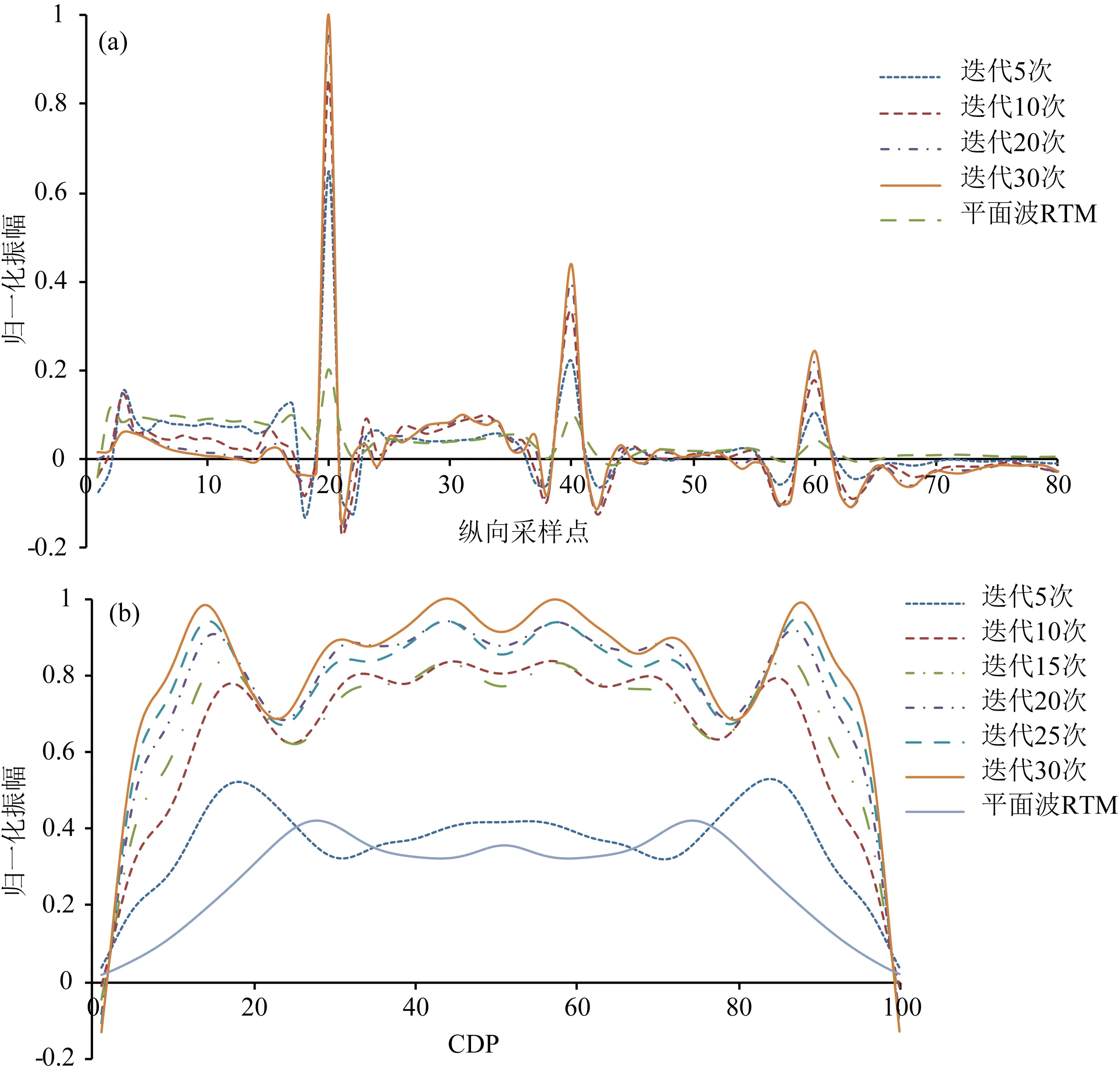
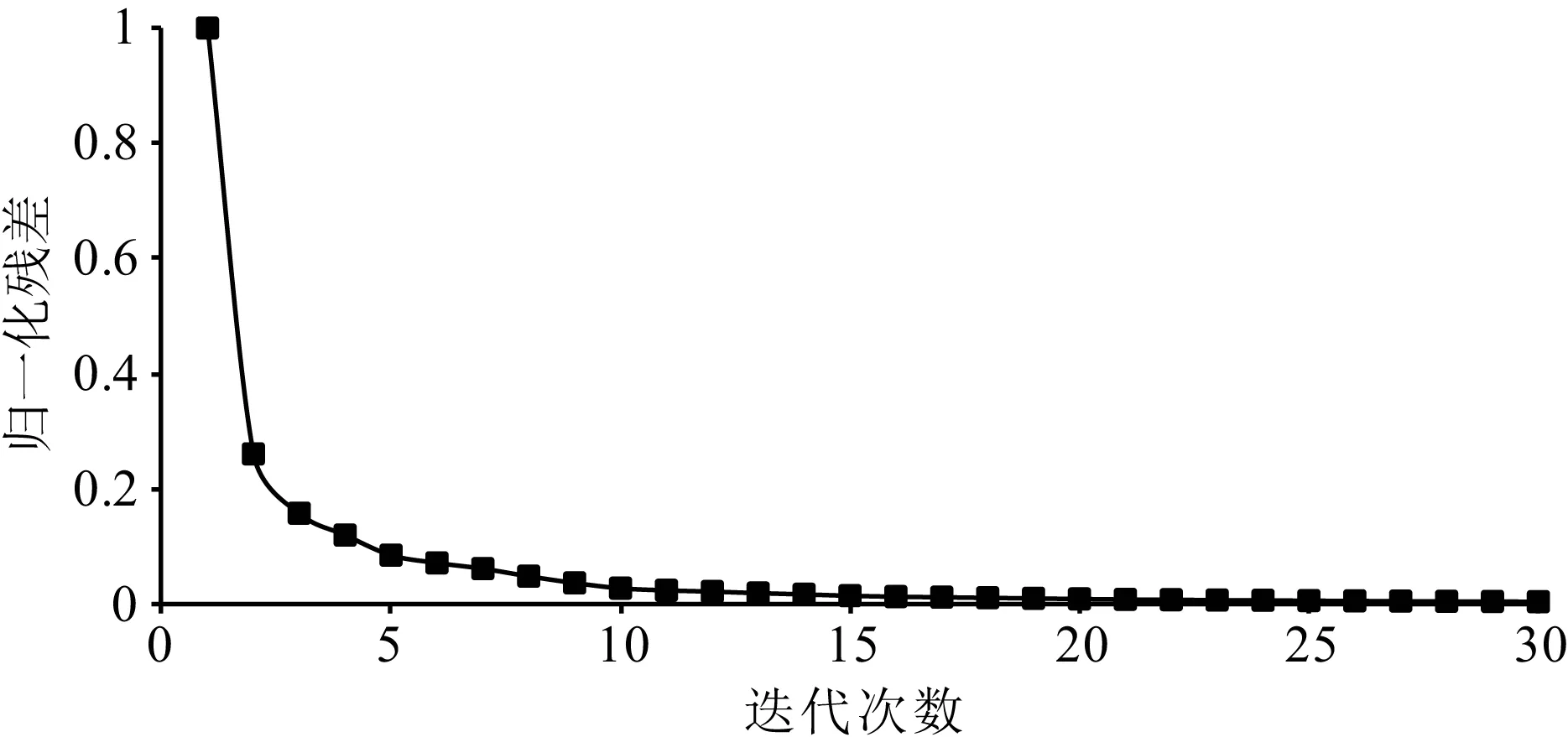
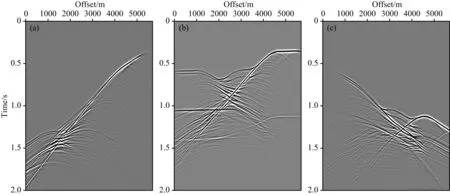
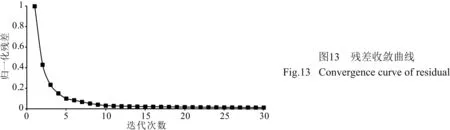
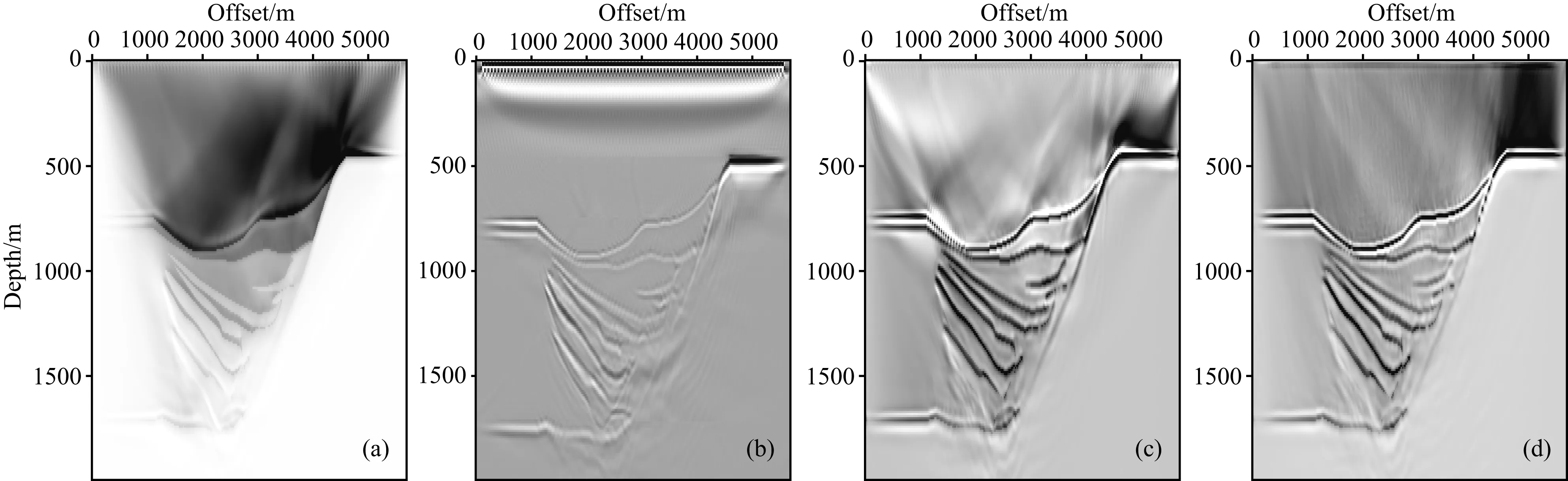
(3)判断是否满足条件k1

(5)更新反射率模型m(k+1)=m(k)-α(k+1)z(k+1)，k=k+1，k1=k1+1.

平面波最小二乘逆时偏移的实现流程如图2所示，其中初始模型赋0值，即第一次迭代的结果为逆时偏移的偏移剖面，在随后的迭代中通过公式(11)

图2 平面波最小二乘逆时偏移实现流程Fig.2 Flow chart of plane-wave LSRTM

使其向真实的反射率模型收敛.通过平面波编码压缩数据将Ns个炮记录压缩为Np个平面波记录，最小二乘逆时偏移的计算效率可提高Ns/(Np×2)倍.需要强调的是，在反偏移时仍然要对震源进行平面波编码，且与炮记录的编码是一一对应的.

图3 平层模型速度场Fig.3 Horizontal layered velocity model

3 模型试处理

3.1 平层模型

在编程实现方法的基础上，本文建立了如图3所示的平层模型进行成像方法正确性测试.其中，模型参数为：深度方向80个采样点，水平方向100个采样点，网格间距10 m.其次，计算参数如下：震源为主频30 Hz 的雷克子波，时间采样间隔0.5 ms，时间采样点2101个，使用时间2阶、空间8阶有限差分正演模拟.观测系统的设计：总炮数101炮，101道检波器接收，炮间距和道间距都为10 m.

使用如上参数计算得到炮记录后，根据公式(3)合成不同参数p的平面波记录，p的取值范围为-0.25～0.25 ms·m-1(对应的倾角范围-30°～ 30°)，呈线性变化，共合成24个平面波记录.图4展示了3个不同角度的平面波道集(已切除直达波).

图5为对如图4b所示的平面波记录(p=0.0 ms·m-1)RTM成像结果，剖面中含有较强的低频噪音、串扰噪音以及震源效应，剖面信噪比及分辨率不高.

该平面波记录(p=0 ms·m-1)的P-LSRTM成像结果如图6所示，从图6可知，随着迭代次数增加震源效应减弱；深部反射同相轴能量逐渐增强；成像剖面信噪比和分辨率得到改善；但对于由稀疏采集产生的串扰噪音的压制效果较差.

为了进一步压制串扰噪音，本文将24个平面波记录偏移结果叠加起来，结果如图7所示.由图7可以看到，串扰噪音基本被压制，剖面分辨率和信噪比也得到了改善.对于不同倾角的平面波记录，其偏移产生的串扰噪音相干性差，因此通过叠加不同倾角的平面波偏移结果，可以使反射同相轴能量增强，压制串扰噪音.此外，平面波源具有方向性，其照射方向与目标结构方向垂直时成像分辨率最高(冯伟等，2004).对于平层模型，p=0 ms·m-1时成像分辨率最高，来自其他p参数的成像结果的叠加可以压制串扰噪音，但在一定程度上降低了叠加结果的分辨x率.当模型复杂时，这一分辨率差异的现象将不再明显.

图4 p取值为-0.25 ms·m-1 (a)， 0 ms·m-1 (b)， 0.25 ms·m-1 (c) 时的平面波记录Fig.4 Plane-wave records with p= -0.25 ms·m-1 (a), p=0 ms·m-1 (b), p=0.25 ms·m-1 (c)

图5 P-RTM偏移结果Fig.5 Image of P-RTM

为了更清楚地观察平面波LSRTM对反射同相轴的能量补偿效果，本文提取了偏移距为500 m时(图7a实线所示)P-RTM和P-LSRTM的单道记录对比，对比结果如图8a所示，随迭代次数增加，P-LSRTM结果振幅能量增强，更接近雷克子波的形态，其保幅性优于常规P-RTM.

图8b展示了P-RTM和P-LSRTM深层反射同相轴(图7a中虚线位置所示)的振幅对比，主要探究P-LSRTM对横向振幅均衡性的改善效果.由图8b可知，由于深部的照明效果较差，P-RTM结果反射振幅弱，且横向振幅能量不均衡；而P-LSRTM的横向振幅能量及均衡性均随迭代次数增加而变强.

P-LSRTM的残差收敛曲线如图9所示，由图9可知，成像反演结果较为稳定；随着迭代次数的增加，残差逐渐减小，成像结果逐渐趋近于真实模型；在第10次迭代时结果已基本收敛.

通过平层模型正演及偏移成像结果，验证了本文方法的正确性.

3.2 砂砾断块模型

在验证了偏移方法正确性的基础上，本文引入了胜利某探区典型的砂砾断层模型，对方法的适应性进行测试.计算用到的模型如图10所示，模型水平方向大小为5.7 km，深度方向为2.0 km，网格间距10 m，上覆岩层厚度约700 m，模型右侧为一个高速的高陡倾构造.模型自上而下依次分布5个高速小断块体，且埋藏较深，倾角较大，断块间间距小，分界不明显.由于高速断块体造成的深部照明不足、强烈的横向变速以及模糊的断块边界都将给断块体的高精度成像带来巨大的挑战.

成像测试的计算参数为：震源为主频30 Hz的雷克子波，网格间距10 m，时间采样间隔0.5 ms，采集时长2 s，使用时间2阶、空间8阶有限差分正演模拟.观测系统的设计：总炮数571炮，571道检波器接收，炮间距和道间距均为10 m.

使用如上参数计算得到炮记录后，根据公式(3)合成不同参数p的平面波记录，p的取值范围为-0.1742～0.1742 ms·m-1，呈线性变化，共合成24个平面波记录.图11展示了3个不同角度的平面波道集(已切除直达波)，可以看到反射同相轴十分复杂、错乱.

图12为24个平面波记录P-LSRTM成像后的叠加结果，由图12可知，在残差收敛过程中，由成像产生的低频噪音和串扰噪音得到压制；反射同相轴能量增强；深部反射同相轴能量均衡性变好；但对成像结果右侧平层上的强低频噪音不能完全压制，这可能是模型右侧的平层反射系数过大造成的.根据Zhang等(2005)给出的计算公式，需要90个平面波记录偏移结果的叠加才能完全压制串扰噪音，但是LSRTM本身具有压制噪音的作用，因此本文只叠加了24个平面波记录，串扰噪音已基本压制.

图6 P-LSRTM迭代5次(a)、10次(b)、15次(c)、20次(d)、25次(e)、30次(f)偏移结果(p=0 ms·m-1)Fig.6 Image of P-LSRTM after 5(a),10(b),15(c),20(d),25(e),30(f) iterations (p=0 ms·m-1)

图7 P-LSRTM迭代5次(a)、10次(b)、15次(c)、20次(d)、25次(e)、30次(f)的叠加结果Fig.7 The stacked image of P-LSRTM after 5 (a),10 (b),15 (c),20 (d),25 (e),30 (f) iterations

图8 保幅性及能量均衡性对比(a) 单道振幅对比(Offset=500 m)； (b) 横向振幅对比(图2红线所示).Fig.8 Comparison of amplitude preservation and energy equilibrium(a) Comparison of vertical amplitude at CDP=50； (b) Comparison of horizontal amplitude (the red line showed in Fig.2).

图9 残差收敛曲线Fig.9 Convergence curve of residual

图10 砂砾断层模型速度场Fig.10 Gravel fault model velocity model

P-LSRTM的残差收敛曲线如图13所示，由图13可知，成像反演结果稳定；对于复杂模型，10次迭代后数据残差基本收敛.

图14为几种常用叠前深度偏移算法的成像对比，由图14(a—d)可知，RTM成像剖面中含有较强的低频偏移噪音，在一定程度上掩盖了地下的真实构造，尤其是深层构造难以辨认；SSF对高陡倾构造成像效果差；LSRTM成像质量最高，低频噪音得到压制，深层反射轴能量得到补偿，高陡构造和小断块都准确地成像；平面波LSRTM成像质量接近LSRTM.

图11 p取值为 -0.1742 ms·m-1 (a)、0 ms·m-1 (b)、0.1742 ms·m-1 (c) 时的平面波记录Fig.11 Plane-wave records with p=-0.1742 ms·m-1 (a), p=0 ms·m-1 (b), p=0.1742 ms·m-1 (c)

图12 P-LSRTM迭代5次(a)、10次(b)、15次(c)、20次(d)、25次(e)、30次(f)的叠加结果Fig.12 The stacked image of P-LSRTM after 5(a),10(b),15(c),20(d),25(e),30(f) iterations

图14 各偏移方法成像效果对比(a) 逆时偏移； (b) 分步傅里叶法偏移； (c) 最小二乘逆时偏移(迭代30次)； (d) 平面波最小二乘逆时偏移(迭代30次).Fig.14 Comparison of images of different pre-stack migration methods(a) RTM； (b) SSF； (c) LSRTM(after 30 iterations)； (d) P-LSRTM(after 30 iterations).

LSRTM迭代一次所用的时间是RTM的2倍，计算效率低.通过平面波编码压缩数据，P-LSRTM的计算时间是炮域RTM的24×30×2/571≈2.52倍.RTM偏移时需要先读取炮记录并存入内存，P-LSRTM存入内存的数据量为RTM的24/571≈0.042倍.

4 结论与讨论

本文发展了基于静态平面波编码的最小二乘逆时偏移方法，在实现算法的基础上，通过对简单平层模型和复杂砂砾断块模型的成像试处理以及与其他几种叠前偏移方法的对比，得到了如下认识：

(1)基于平面波编码的LSRTM成像算法能够较好地抑制RTM算法中的低频噪音，减弱稀疏采集造成的震源效应，补偿深层反射同相轴能量，对复杂小构造的高精度成像具有一定的优势；

(2)串扰噪音可以通过叠加不同倾角的偏移剖面压制，此外迭代次数的增加也对串扰噪音有一定的压制作用；

(3)通过平面波编码压缩数据体，提高了计算效率，减小了I/O消耗，提高了最小二乘高精度成像理论方法在生产中应用的可能性.

基于静态平面波编码的最小二乘逆时偏移对不同角度的平面波记录分别进行偏移，计算效率高，有利于平面波域共成像点道集和角道集的提取，可用于成像质量的控制和偏移速度分析.但是，本文所实现的平面波编码只适用于固定的观测系统，无法处理炮点和接收点分布不固定的情况.因此，角道集的提取以及适用于非固定观测系统的P-LSRTM方法都将是作者下一步研究的重点.

Baysal E, Kosloff D D, Sherwood J W C. 1983. Reverse time migration.Geophysics, 48(11): 1514-1524.

Berkhout A J. 1992. Areal shot-record technology.JournalofSeismicExploration, 1(3): 251-264.

Beydoun W B, Mendes M. 1989. Elastic ray-born L2-migration/inversion.GeophysicalJournalInternational, 97(1): 151-160.

Dai W, Schuster J. 2009. Least-squares migration of simultaneous sources data with a deblurring filter. ∥ SEG Houston International Exposition and Annual Meeting. 2990-2994. Dai W, Boonyasiriwat C, Schuster G T. 2010. 3D multi-source least-squares reverse time migration. ∥ 2010 SEG Technical Program Expanded Abstracts 2010: 3120-3124.

Dai W, Wang X, Schuster G T. 2011. Least-squares migration of multisource data with a deblurring filter.Geophysics, 76(5): R135-R146.

Dai W, Fowler P, Schuster G T. 2012. Multi-source least-squares reverse time migration.GeophysicalProspecting, 60(4): 681-695.

Dai W, Schuster G T. 2013. Plane-wave least-squares reverse-time migration.Geophysics, 78(4): S165-S177. Kuehl H, Sachhi M D. 2001. Split-step WKBJ least-square migration / inversion of incomplete data. ∥5th SEGJ International Symposium Imaging Technology. Kuehl H, Sacchi M D. 2003. Least-squares wave-equation migration for AVP/AVA inversion.Geophysics, 68(1): 262-273. Lambare G, Virieux J, Madariaga R, et al. 1992. Iterative asymptotic inversion in the acoustic approximation.Geophysics, 57(9): 1138-1154. LeBras R, Clayton R W. 1988. An iterative inversion of back-scattered acoustic waves.Geophysics, 53(4): 501-508.

Li C, Huang J P, Li Z C, et al. 2014. Application of plane-wave least square migration in fault block reservoirs-a case study. ∥76th EAGE Conference and Exhibition.

Luo Y, Schuster G T. 1991. Wave-equation traveltime inversion.Geophysics, 56(5): 645-653.

Mosher C C, Foster D J, Hassanzadeh S. 1997. Common angle imaging with offset plane waves. ∥Expanded Abstract of 67th Annual Internat SEG Mtg., 1379-1382.

Nemeth T, Wu C J, Schuster G T. 1999. Least-squares migration of incomplete reflection data.Geophysics, 64(1): 208-221.

Stoffa P L, Fokkema J T, de Luna Freire R M, et al. 1990. Split-step Fourier migration.Geophysics, 55(4): 410-421.

Zhang Y, Sun J, Notfors C, et al. 2005. Delayed-shot 3D depth migration.Geophysics, 70(5): E21-E28.

附中文参考文献

陈开周. 1985. 最优化计算方法. 西安: 西北电讯工程学院出版社.

陈生昌, 曹景忠, 马在田. 2002. 平面波偏移. 勘探地球物理进展, 25(3): 37-41.

冯伟, 王华忠, 吴如山等. 2004. 面向目标控制照明的合成波源偏移. 石油物探, 43(3): 223-228.

郭振波, 李振春. 2014. 最小平方逆时偏移真振幅成像. 石油地球物理勘探, 49(1): 113-120.

黄建平, 李振春, 孔雪等. 2013a. 碳酸盐岩裂缝型储层最小二乘偏移成像方法研究. 地球物理学报, 56(5): 1716-1725.

黄建平, 李振春, 刘玉金等. 2013b. 复杂介质最小二乘叠前深度偏移成像方法. 地球物理学进展, 28(6): 2977-2983.

黄建平, 曹晓莉, 李振春等. 2014a. 最小二乘逆时偏移在近地表高精度成像中的应用. 石油地球物理勘探, 49(1): 107-112.

黄建平, 薛志广, 步长城等. 2014b. 基于裂步DSR的最小二乘偏移方法. 吉林大学学报: 地球科学版, 44(1): 369-374.

黄建平, 孙郧松, 李振春等. 2014c. 一种基于分频编码的最小二乘裂步偏移方法. 石油地球物理勘探, 49(4): 702-707.

贾晓峰, 胡天跃. 2005. 滑动最小二乘法求解地震波波动方程. 地球物理学进展, 20(4): 920-924.

刘玉金, 李振春, 吴丹等. 2013. 局部倾角约束最小二乘偏移方法研究. 地球物理学报, 56(3): 1003-1011.

孙沛勇, 张叔伦. 2000. 平面波最大能量叠前深度偏移. 石油地球物理勘探, 35(3): 283-289.

王彦飞. 2007. 反演问题的计算方法及其应用. 北京: 高等教育出版社.

夏颖, 祝彩霞, 孙灵群. 2008. 地震勘探仪器在高密度采集中的应用. 物探装备, 18(1): 7-10, 21.

杨海生, 王必金, 陈玉明, 等. 2011. 基于起伏地表的合成平面波叠前深度偏移. 石油物探, 50(2): 129-138.

杨其强, 张叔伦. 2008. 最小二乘傅立叶有限差分法偏移. 地球物理学进展, 23(2): 433-437.

叶月明, 李振春, 仝兆岐等. 2007. 起伏地表条件下的合成平面波偏移及其并行实现. 石油地球物理勘探, 42(6): 622-628.

张叔伦, 孙沛勇. 1999. 基于平面波合成的傅里叶有限差分叠前深度偏移. 石油地球物理勘探, 34(1): 1-7.

赵会欣, 晋志刚, 张宇生等. 2008. 高密度空间采样地震采集覆盖次数的选择. 天然气工业, 27(增刊A): 68-69.

(本文编辑 胡素芳)

Least-squares reverse time migration with static plane-wave encoding

HUANG Jian-Ping1, LI Chuang1*, LI Qing-Yang1, GUO Shu-Juan2, DUAN Xin-Biao2,LI Ji-Guang3, ZHAO Sheng-Tian3, BU Chang-Cheng3

1DepartmentofGeophysics,ChinaUniversityofPetroleum(EastChina),Qingdao266580,China2SINOPECGeophysicalResearchInstitute,Nanjing210000,China3ShengliGeophysicalResearchInstituteofSINOPEC,DongyingShandong257000,China

To solve the exploration problem of widely distributed fault block reservoirs in China, high-density seismic acquisition methods with small surface element and high coverage times become more popular recently which results in the huge dataset for seismic processing. Plane-wave migration is a kind of areal shot migration method which can process enormous data of high-density acquisition with much higher computational efficiency compared with shot domain migration. But conventional plane-wave migration produces low quality images with crosstalk. To solve these problems, the paper introduces the plane-wave migration to the inversion framework and presents the theory and work flow of least-squares reverse time migration with static plane-wave encoding.The key points of plane-wave least squares reverse time migration can be divided into two parts. Firstly, the plane-wave decomposition is applied to the shot data which can be performed by using some delayed-shot variant of slant-stack processing. This involves applying a linear time delay to the shot records. And the time delay is also applied to the corresponding sources. Note that there is one-to-one correspondence between source encoding and encoding to common shot gathers. The input data of migration is compressed a lot after plane-wave encoding which improves the computational efficiency. Secondly, the misfit function of plane-wave least squares reverse time migration is defined as the data difference between predicted plane-waves by Born modelling and observed plane-waves in the pre-stack migration. The conjugate gradient method is implemented to find the solution that minimizes the misfit function. However, the searching of CG method becomes very slow after several iterations in practical application, so we set the steepest descent direction as the gradient after several iterations to restart the CG method. One other thing to note is that the migration results are updated separately with different plane-waves and stacked together after the iterations are finished.The plane-wave least squares reverse time migration is firstly tested via the synthetic data set with the three layer medium model to verify the validity of the proposed method. The plane-wave reverse time migration is also applied to the model for better comparison. The comparison of imaging quality, vertical amplitude and transverse amplitude balance are presented which illustrates the advantages of the proposed method. The stable convergence also proves the robustness of the method. Then, the proposed method is applied to a complex fault block model in Shengli Oil-field to test its applicability. Several fault blocks are distributed in the mid-deep part and a high steep structure locates on the right of the model. The strong velocity variation, the burial depth and fuzzy boundary of fault blocks make it a good velocity model to test the resolution of the imaging method. The imaging results of the proposed method is compared with the reverse time migration, the split step migration and least-squares revere time migration results, which show that the proposed method can produce high quality images similar to least-squares reverse time migration but onlynp/nstimes computation is needed (nsis the number of the shots andnpis the number of the encoded plane-waves).The paper presents the theory of prestack least-squares reverse time migration with a static plane-wave encoding technique. From the imaging test we can get the conclusions including: (1) the proposed method has the advantages of resolution enhancement and amplitude compensation in mid-deep part with the increase of iterations; (2) the crosstalk introduced by plane-waves can be suppressed by the stacking of images from different plane-waves and the optimization; (3) the computation and input/output cost is reduced a lot with the plane-waves encoding. Besides, the common image gathers can be extracted efficiently from the migration results of the proposed method which is also available for the migration velocity analysis and our next work will be focused on this part. However, the proposed method is only implemented with the fixed geometry and another point of our next work is to modify the method to fit irregular geometry.

Plane-wave migration； Lithology imaging； Plane-wave encoding； Least-square migration； Amplitude persevered migration

10.6038/cjg20150619.

国家973课题(2014CB239006，2011CB202402)，国家自然科学基金(41104069，41274124)，山东省自然科学基金(ZR2011DQ016)，中央高校科研业务费专项基金(R1401005A)联合资助.

黄建平，男，1982年生，副教授，主要从事地震波正演及偏移成像工作.E-mail：jphuang@mail.ustc.edu.cn

*通讯作者 李闯,男, 1992年生, 博士生，主要研究方向为地震波最小二乘逆时偏移. E-mail:chli0409@126.com

10.6038/cjg20150619

P631

2014-05-28，2015-03-19收修定稿

黄建平， 李闯， 李庆洋等. 2015. 一种基于平面波静态编码的最小二乘逆时偏移方法.地球物理学报，58(6):2046-2056,

Huang J P, Li C, Li Q Y, et al. Least-squares reverse time migration with static plane-wave encoding.ChineseJ.Geophys. (in Chinese),58(6):2046-2056,doi:10.6038/cjg20150619.