2015年尼泊尔MS8.1地震的地壳重力均衡背景与地表形变响应特征
付广裕, 高尚华, 张国庆, 佘雅文, 孙和平
1 中国地震局地震预测重点实验室(中国地震局地震预测研究所), 北京 100036 2 大地测量与地球动力学国家重点实验室, 武汉 430077
2015年尼泊尔MS8.1地震的地壳重力均衡背景与地表形变响应特征
付广裕1,2, 高尚华1*, 张国庆1, 佘雅文1, 孙和平2
1 中国地震局地震预测重点实验室(中国地震局地震预测研究所), 北京 100036 2 大地测量与地球动力学国家重点实验室, 武汉 430077
对2015年尼泊尔MS8.1地震的地壳均衡背景及其引起的地表形变特征进行了研究,结果表明:(1)尼泊尔MS8.1地震震中以南的印度板块岩石圈有效弹性厚度大约为9 km,加载主要来自地幔;地震以北的拉萨地块岩石圈有效弹性厚度大约为2 km,加载主要来自地表.(2)尼泊尔MS8.1地震震中以南地区的地壳均衡异常大约为-100 mGal(10-5m·s-2),但其北部的地壳均衡异常则为300~400 mGal,尼泊尔MS8.1地震发生在地壳均衡负异常向正异常过渡的高梯度带上.(3)尼泊尔MS8.1地震使震中周围地区的地壳整体向南运动,最大水平位移超过1.5 m,分布在震中东南.震中以北的同震垂向位移总体为负值,最大下降幅度超过0.5 m,同震重力变化总体为正值,最大超过60 μGal(10-8m·s-2);震中以南的垂向位移总体为正值,最大升幅超过0.7 m,同震重力变化总体为负值,最大降幅超过-120 μGal. (4)尼泊尔MS8.1地震使“世界屋脊”喜马拉雅山脉产生沉降,最大同震降幅超过120 mm,震后松弛效应将使“世界屋脊”持续缓慢下降.该强震使世界最高峰珠穆朗玛峰降低了2~3 mm,有可能被GPS、InSAR等现代大地测量工具检测到.
2015年尼泊尔MS8.1地震; 岩石圈有效弹性厚度; EGM2008重力场模型; 球体位错理论; 喜马拉雅山脉
1 引言
北京时间2015年4月25日14时11分,在喜马拉雅山脉南麓的尼泊尔(北纬28.2°,东经84.7°)发生MS8.1地震,震源深度约为20 km(中国地震台网测定),造成8000以上人员死亡,1万以上人员受伤,许多珍贵文物损坏,同时还造成珠穆朗玛峰雪崩,触发我国西藏日喀则地区定日县5.9级地震和聂拉木县5.3级地震.尼泊尔MS8.1地震的余震多发生在震中东南,总体分布在长约140 km、宽约40 km的范围内,其中包括3次7级以上强余震.本次地震是由于印度板块低角度俯冲到欧亚板块之下冲造成的,属于典型的俯冲型地震.震中处于喜马拉雅块体上,该块体位于印度—欧亚大陆主碰撞带的前沿部位,喜马拉雅造山带的中段,距离尼泊尔首都加德满都约80 km.
跨喜马拉雅山脉的GPS观测显示,西藏南部与尼泊尔之间的相对运动速率为17 mm·a-1(王琪等,1998).北向运动的印度板块俯冲到欧亚板块之下,导致了非常多的地震,使喜马拉雅构造带成为一条全球知名的地震带.历史上,沿这条长达2500 km的喜马拉雅构造带发生过多次8级及以上巨大地震,仅20世纪就有:1905年印度8.0级地震、1934年尼泊尔比哈尔邦8.1级地震和1950年我国察隅8.6级地震,早年有记录的大地震还有1505年尼泊尔格尔纳利河8.2级地震,等等(Bollinger et al., 2014).本次地震位于1934年地震和1505年地震之间的地震空区内,靠近1934年地震的西北部.
尼泊尔MS8.1地震发生在喜马拉雅山脉附近,是21世纪以来第五次八级以上内陆强震,也是本世纪距离世界最高峰珠穆朗玛峰最近的8级以上强震.该强震的发震背景如何?对“世界屋脊”喜马拉雅山脉造成了什么样的影响?是否再次抬升了地球最高峰珠穆拉玛峰的高度?等等,都是值得关注的科学问题.本研究计划依据地球重力场模型EGM2008和地形模型Topo,用重力导纳方法(Fielding and McKenzie,2012)研究尼泊尔MS8.1地震周边地区岩石圈有效弹性厚度和加载机制,给出区域重力均衡分布与该地震之间的位置关系;本研究还计划利用球体位错理论(Tanaka et al.,2006;Sun et al.,2009)研究尼泊尔MS8.1地震引起的同震与震后位移与重力变化,计算该地震发生后喜马拉雅山脉,包括穆拉玛峰,的高度变化,为阐明“世界屋脊”的后续演化规律提供地震形变场理论参考.
2 尼泊尔MS8.1地震周边地区岩石圈有效弹性厚度及其加载机制
岩石圈有效弹性厚度Te定义为与岩石圈板块中实际应力分布所产生的弯矩相等的弯曲弹性板的厚度,标志着在地质时间尺度内,岩石圈承受超过100 MPa压力时,发生弹性行为向流体行为转变的深度(付永涛等,2000;胡敏章等,2015).Te的确定,对认识其力学性质及演化过程等问题具有重要意义(杨亭等,2012),可为板块动力学模型的构建、岩石圈挠曲形变动力学机制等研究提供依据(胡敏章等,2015).地震活动是断层活动的结果,由挠曲加载产生的弯曲应力可能是引起地壳断裂的应力来源之一,可以通过重力导纳方法(McKenzie,2003)计算.全球范围的活动造山带Te的分布与相应深度发震次数的分布极为相似,因此Te与地震活动之间存在密切的联系(Watts,2001).
本文通过地球重力场数据,利用自由空气重力导纳方法(Watts, 2001),计算尼泊尔MS8.1地震震中周围地区岩石圈有效弹性厚度Te及其加载位置.自由空气重力导纳方法是通过分析自由空气重力异常和相应地区地形的波数域相关性来估计Te和形成挠曲的加载位置.本文使用McKenzie(2003)给出的计算方法进行研究,可有效消除自由空气重力异常与地形不相关的干扰成分.
本文使用EGM2008自由空气重力异常数据及其配套的DEM数据(研究区域为102°E—110°E,33°N—38°N)计算导纳值.具体地说,为了压制数据中高频成分的影响,分别对重力数据和DEM数据在频率域进行了50 km和20 km的低通滤波处理(Fielding and McKenzie,2012),可在确保去除低频成分的同时,得到较高的重力与地形的相关性.在对自由空气重力异常与DEM数据进行谱估计的计算中,使用多窗谱分析方法(Thomson,1982)将空间域的数据转换为波数域数据,该方法可减小频谱泄露,同时可增加频峰宽度,减少信息丢失,提高频谱分辨率.在模型参数中,不同的Te和加载比Ff(F1、F2和F3分别代表地表加载、上地壳和下地壳界面加载以及地幔与下地壳界面加载在总加载中所占比例,且F1+F2+F3=1)对应不同的理论导纳,在得到模型导纳和实测导纳之后,使二者拟合度最佳的Te和加载比Ff即为研究区域岩石圈有效弹性厚度Te和加载比.
Bai等(2013)系统分析了喜马拉雅山脉和拉萨地块三维岩石圈密度构造,发现喜马拉雅山脉南北地壳地幔结构明显差异.本文依据Bai等(2013)的研究成果,以尼泊尔MS8.1地震震中附近的喜马拉雅山脉为界,分别设定岩石圈密度参数.在喜马拉雅山脉以北,上地壳深度为20 km,密度为2.7 g·cm-3,下地壳深度为35 km,密度为2.9 g·cm-3,地幔密度为3.3 g·cm-3(模型1).但在喜马拉雅山脉以南,上地壳深度为20 km,密度为2.7 g·cm-3,下地壳深度为55 km,密度为2.95 g·cm-3,地幔密度为3.3 g·cm-3(模型2).
根据上述地壳模型参数,本文分别计算区域岩石圈有效弹性厚度与加载机制,结果见图1和图2,分别适用于喜马拉雅山脉以南的印度板块与我国的拉萨地块.图1和图2中,(a)表示自由空气重力导纳计算结果及其拟合曲线,在甚长波长域,自由空气导纳应该为零,图1和图2中,长波长域的计算结果与拟合值的不符合应该与喜马拉雅山脉南北地壳地幔结构明显差异有关;(b)表示自由空气重力导纳的相位角,理想情况下该值为0;(c)表示自由空气重力异常与地形的相干性,理想情况下该值为1;(d)表示实测导纳与模型导纳的不符合度,当不符合度最小时,相应的厚度即为岩石圈有效弹性厚度.
据图1d可知,喜马拉雅山脉以南的印度板块的岩石圈有效弹性厚度大约为9 km,相对坚硬,相应的加载比为F1=0.29,F2=0.11,F3=0.60,该结果表明,印度板块的初始加载主要来自地幔与下地壳界面的深部加载,意味着印度板块岩石圈的加载主要来自深部的地幔.据图2d可知,喜马拉雅山脉以北的拉萨地块的岩石圈有效弹性厚度大约为2 km,相对柔软,相应的加载比为F1=0.78,F2=0.12,F3=0.10,该结果表明,拉萨地块岩石圈的加载主要来自地表荷载.综合图1和图2可知,来自深部地幔的驱动力驱动坚硬的印度板块北向运动,挤压北部相对柔软的拉萨地块;拉萨地块被动承受来自印度板块的挤压、变形,形成喜马拉雅等山脉,山脉自身物质的重量是拉萨地块岩石圈的主要加载来源.
3 尼泊尔MS8.1地震周边地区地壳重力均衡分布
依据岩石圈弹性板均衡模型,利用布格重力异常数据和DEM数据,可以计算弹性板均衡重力异常(陈石等,2011).依据上述思路,本文研究了尼泊尔MS8.1地震震中周围地区地壳重力均衡分布.布格重力异常为EGM2008模型给出的自由空气重力异常数据、经过地形改正后获得的布格重力异常数据(图3).由于采样点较密集,在进行地形重力校正时,将近场、中场和远场的网格地形数据分别定义为5″×5″、25″×25″和50″×50″,以减少计算时间.地形数据为Topo V18.1版本的DEM数据.本文使用的数据范围为东经80°E—90°E,北纬21°N—35°N,以避免傅里叶变换的边缘效应,最后采用中心区域(东经82°E—88°E,北纬26°N—30°N)的均衡重力异常,结果见图4.
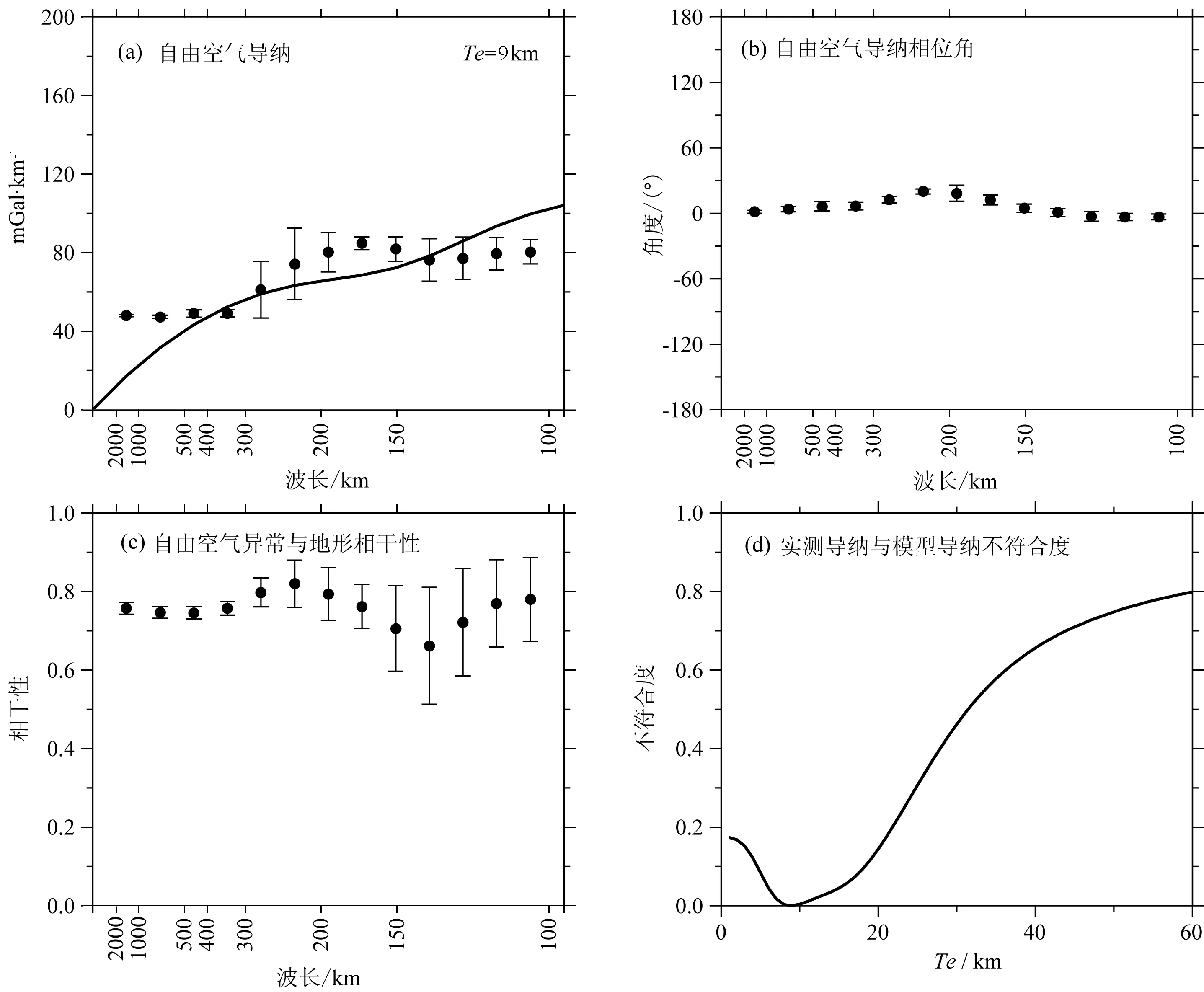
图1 尼泊尔MS8.1地震以南印度板块自由空气重力导纳与岩石圈有效弹性厚度Fig.1 The free-air gravity admittance and the lithosphere effective elastic thickness at Indian block, south to the Nepal MS8.1 earthquake
图3显示,尼泊尔MS8.1地震以北的拉萨地块的布格重力异常为显著的负异常,最大达到-600 mGal左右.地震以南布格重力异常较小,在-100 mGal左右变动.喜马拉雅山区的布格重力异常变化显著,短波长信息较多.
依据图3给出的布格重力异常数据,结合第2节给出的地壳模型1(基于印度板块岩石圈建立的地壳模型)和模型2(基于拉萨地块岩石圈建立的地壳模型),分别计算区域地壳均衡异常分布.计算结果显示,两种岩石圈模型对应的地壳均衡异常总体分布基本一致.图4给出了模型1对应的地壳均衡分布模型.该图显示,尼泊尔MS8.1地震以南地区的地壳均衡异常大约为-100 mGal左右,北部的喜马拉雅山脉地区的地壳正均衡异常可达到300~400 mGal.尼泊尔MS8.1地震就发生在地壳均衡负异常向正异常过渡的高梯度带上.喜马拉雅山脉以北的拉萨地块,地壳均衡异常大约在0值附近变化.
4 尼泊尔MS8.1地震引起的地表位移与重力变化
4.1 尼泊尔MS8.1地震断层模型
尼泊尔MS8.1地震发生后,USGS网站即刻刊出他们的断层模型反演结果(http:∥earthquake.usgs.gov/earthquakes/eventpage/us20002926 scientific_finitefault [2015-04-27];张贝等,2015),为我们的正演分析提供了断层模型数据.Hayes从NEIC 波形服务中心下载宽带GSN波形数据,根据数据质量及台站分布,选取并分析了其中的42条远震宽频带P波波形数据,15条宽频带SH波波形数据,和62条长周期表面波数据.Hayes首先把波形数据转换成位移数据,然后利用有限断层反演方法(Ji et al., 2002)约束尼泊尔MS8.1地震的断层破裂过程.反演结果表明,尼泊尔MS8.1地震释放的能量大约为8.1×1027达因(10-5kg·m·s-2),对应的矩阵级为Mw7.9,断层的方位角为295°,是一个倾角为10°的低倾角俯冲断层(图5).图5中,五角星表示震源所在位置,白色线条为“世界屋脊”喜马拉雅山脉,红色三角为世界最高峰珠穆拉玛峰.色标表示断层面滑动量.结果表明,断层的最大滑动量超过3 m,分布在震中东南.本文依据图5给出的断层模型进行正演计算.
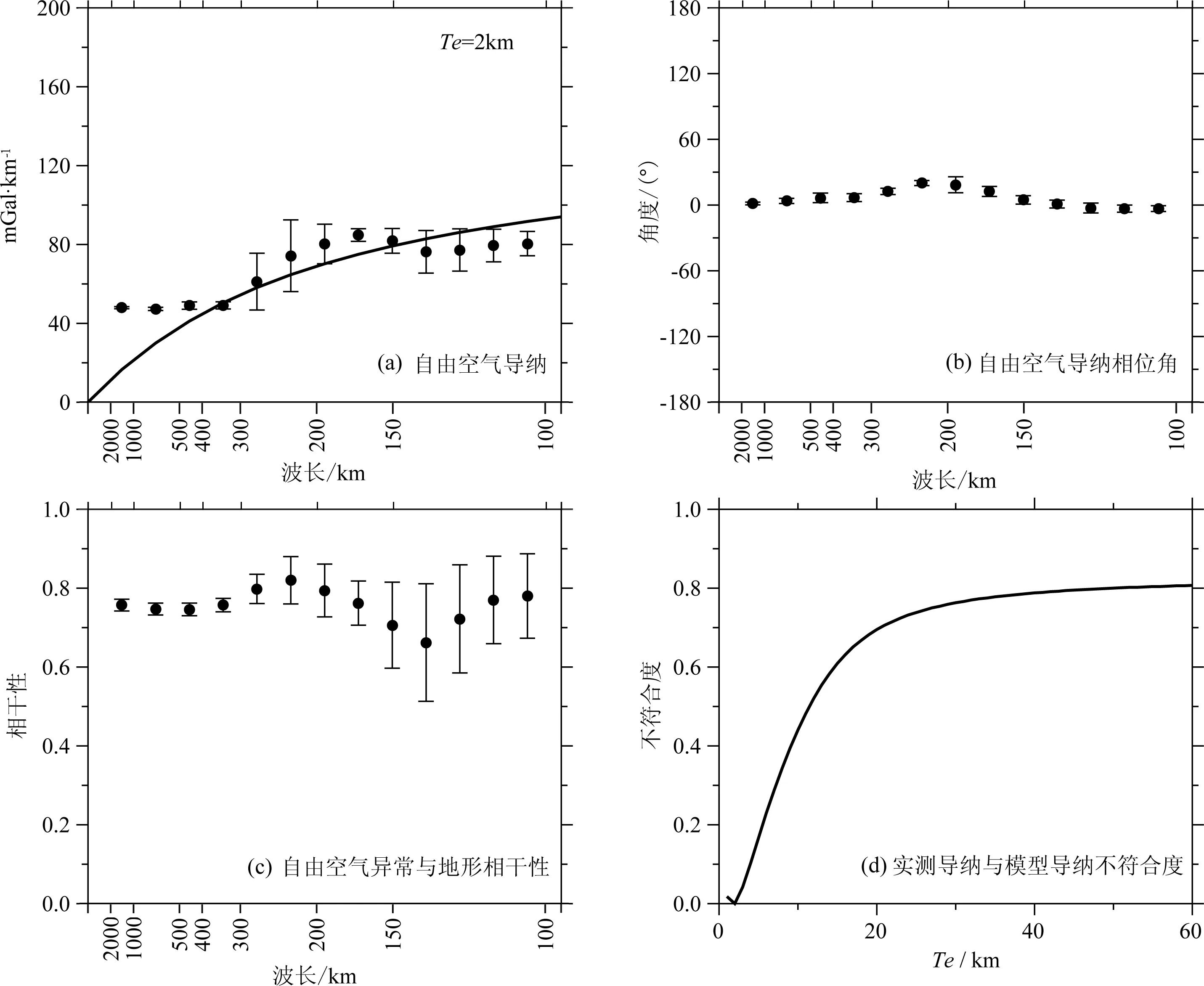
图2 尼泊尔MS8.1地震以北拉萨地块自由空气重力导纳与岩石圈有效弹性厚度Fig.2 The free-air gravity admittance and the lithosphere effective elastic thickness at Lhasa block, north to the Nepal MS8.1 earthquake
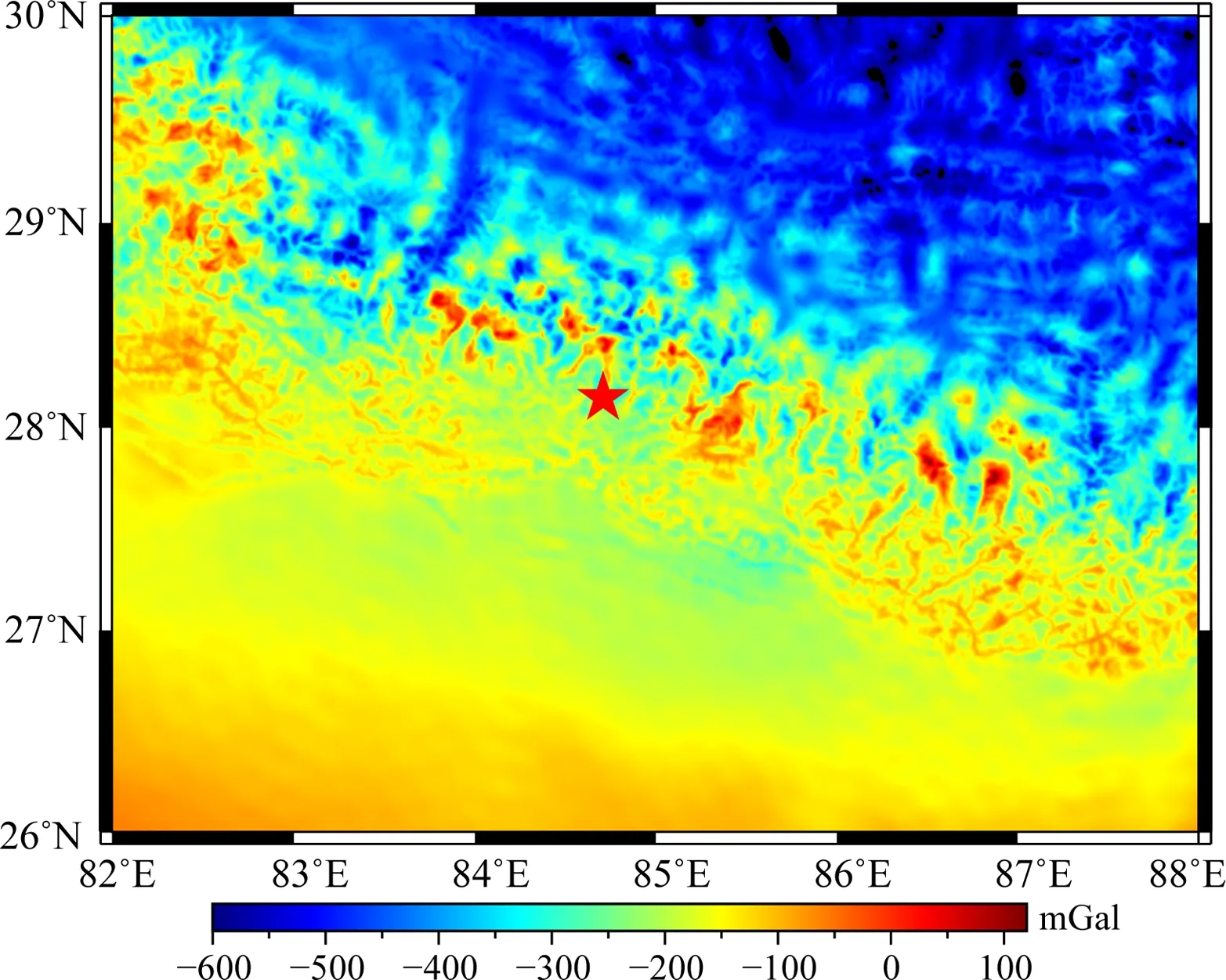
图3 EGM2008给出的尼泊尔MS8.1地震周边地区布格重力异常图.红色五角星为尼泊尔MS8.1地震震中位置Fig.3 The Bouguer gravity anomalies around the Nepal MS8.1 earthquake, which are calculated from EGM2008 gravitational model. Red Star denotes the epicenter of the great earthquake
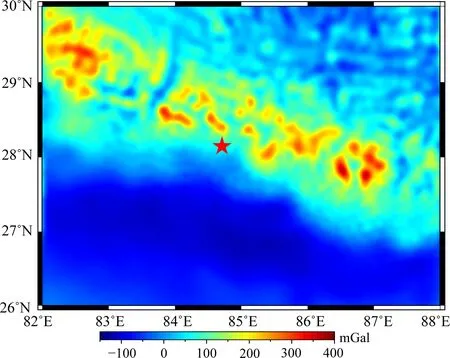
图4 尼泊尔MS8.1地震周边地区地壳均衡异常分布图.红色五角星为尼泊尔MS8.1地震震中位置Fig.4 The isostasy anomalies around the Nepal MS8.1 earthquake. Red Star denotes the epicenter of the great earthquake
4.2 位错理论
位错理论可视为地震发震断层模型与地表形变场之间的一个桥梁,给出一个地震的发震断层模型,就可以利用位错理论计算该地震在地球表面(或内部)产生的同震与震后地壳形变,如位移、应力、应变、倾斜、重力位与重力变化等.Steketee(1958)最早把位错理论引入地震学中,之后很多学者研究了地震的同震与震后形变问题.基于平面半空间地球模型,Okada(1985)总结并整理了前人的研究成果,给出了完整、简洁、实用的地表同震形变计算公式,适用于计算任意剪切与引张位错引起的位移、应变与倾斜变形,并成为平面半空间位错理论的经典表达式.随后,为了考虑地球曲率和层状构造的影响,更高精度地计算同震与震后形变,特别是远场同震形变,Sun和Okubo(1993)、Sun等(1996,2009)以弹性球对称地球模型为基础建立了球体位错理论,Tanaka等(2006, 2007)以黏弹性球对称地球模型为基础建立了黏弹性球体位错理论,提高了位错理论的计算精度.
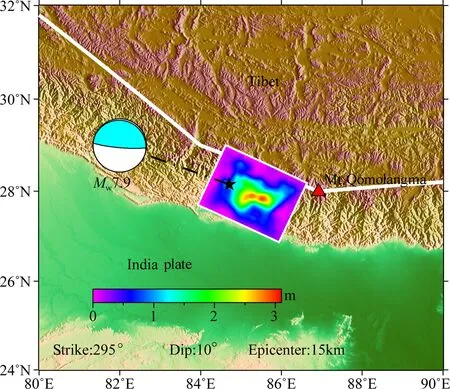
图5 USGS给出的尼泊尔MS8.1地震断层破裂模型Fig.5 Finite fault model of the Nepal MS8.1 earthquake presented by USGS
本文将利用精度较高的球体位错理论(Sun et al.,2009;Tanaka et al.,2006),针对尼泊尔MS8.1地震展开研究,分析该地震对周边地区地壳形变场与重力场的影响.
4.3 尼泊尔8.1地震引起的地表形变与重力变化
首先,本文利用Sun等(2009)给出的弹性球体位错理论,计算了尼泊尔MS8.1地震引起的地表同震位移与重力变化(图6).计算程序来自付广裕和孙文科(2012),地球模型使用PREM模型(Dziewonski and Anderson,1981).
图6a中,箭头代表同震水平位移,色标代表同震垂向位移.尼泊尔MS8.1地震使震中周围地区的地壳整体向南运动,最大值超过1.5 m,发生在震中东南部地区,也就是断层面位移较大、余震分布较为密集的区域.较大的形变集中发生在北纬27.5°N—28.5°N,东经84.5°E—86.0°E之间的长方形区域内部.在断层面以北的喜马拉雅山脉地区,总体同震垂向位移为负值,最大下降幅度超过-0.5 m;而在断层面以南的山麓地区,总体同震垂向位移则为正值,最大上升幅度超过0.7 m.
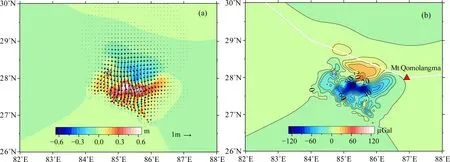
图6 尼泊尔MS8.1地震引起的同震位移(a)与重力变化(b)Fig.6 Co-seismic displacements (a) and gravity changes (b) caused by the Nepal MS8.1 earthquake

图7 尼泊尔MS8.1地震引起的地表震后垂向位移分布图.黑色五角星为尼泊尔MS8.1地震震中(a)震后7年;(b)震后70年.Fig.7 Post-seismic vertical displacements caused by the Nepal MS8.1 earthquake. Black star denote the epicenter of the great earthquake. (a) The vertical displacements at 7 years after the great earthquake; (b) The ones at 70 years after the great earthquake
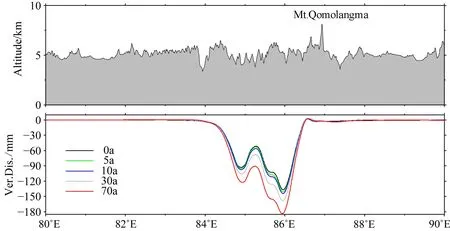
图8 尼泊尔MS8.1地震在喜马拉雅山脉引起的同震与震后垂向位移Fig.8 Co-/post-seismic vertical displacements caused by the Nepal MS8.1 earthquake at the Himalayas
图6b给出尼泊尔MS8.1地震震中周围地区同震重力变化图.白色线条为喜马拉雅山脉,红色三角为珠穆拉玛峰.由此图可知,尼泊尔MS8.1地震断层面北部的喜马拉雅山脉的重力变化总体为正值,最大值超过60 μGal(10-5m·s-2);而在断层面以南的山麓地区,同震重力变化总体为负值,最大下降幅度超过-120 μGal.

图9 尼泊尔MS8.1地震在珠穆朗玛峰引起的同震与震后垂向位移Fig.9 Co-/post-seismic vertical displacements caused by the Nepal MS8.1 earthquake at Mt. Qomolangma
本文利用黏弹性球体位错理论(Tanaka et al.,2006)计算尼泊尔MS8.1地震引起的震后垂向位移,以了解震中周围地区的震后松弛效应.计算程序来自张国庆等(2015),该程序改编自Tanaka给出的黏弹性位错理论(Tanaka et al.,2006)配套计算程序与付广裕和孙文科(2012)给出的弹性球体位错理论配套计算程序.根据石耀霖和曹建玲(2008)的研究可知,青藏高原上地幔黏滞系数可等效为1×1020Pa·s .因此本文在计算过程中,区域地幔黏滞性系数取为1×1020Pa·s .图7给出了震后7年和震后70年震中周围地区垂向位移分布图.与同震垂向位移(图6a)比较后发现,尼泊尔MS8.1地震引起的垂向位移总体分布形态不变,呈现北降南升的态势,但变化幅度和变化区域渐渐变大.
图8的横轴为喜马拉雅山脉(图5中白色折线)对应的经度值.图8给出了尼泊尔MS8.1地震后0、5、10、30和70年在喜马拉雅山脉上引起的垂向位移.总体上,喜马拉雅山脉在尼泊尔MS8.1地震时产生下降,最大同震降幅达到-120 mm左右,随着时间的推移,震后垂向位移还会缓慢增加,70年后可达到-180 mm左右.
图9给出了珠穆朗玛峰因为尼泊尔MS8.1地震而产生的同震与震后垂向位移.由图9可知,尼泊尔MS8.1地震使珠穆朗玛峰下降了2.4 mm以上.震后1年,珠穆朗玛峰的下降量将达到2.5 mm以上.但随着时间的进一步推移,珠穆朗玛峰会缓慢地上升,世界最高峰的高度将再度攀升.珠穆朗玛峰上的震后垂向位移变化趋势与图8所示的喜马拉雅山脉较大垂向位移变化趋势并不完全一致,显示了震后位移的分区性.
5 结论
2015年尼泊尔MS8.1地震发生在喜马拉雅构造带的中部,对周边地区形变场,包括“世界屋脊”喜马拉雅山脉和世界最高峰珠穆朗玛峰,产生了显著的影响.本文对尼泊尔MS8.1地震的地壳重力均衡背景与地表形变响应特征进行了研究,得到以下结论.
(1) 尼泊尔MS8.1地震震中以南的印度板块岩石圈有效弹性厚度大约为9 km,相对坚硬,相应的加载比为F1=0.29,F2=0.11,F3=0.60,意味着印度板块岩石圈的加载主要来自深部地幔.震中以北的拉萨地块岩石圈有效弹性厚度大约为2 km,相对柔软,相应的加载比为F1=0.78,F2=0.12,F3=0.10,意味着拉萨地块岩石圈的加载主要来自地表荷载.
(2) 尼泊尔MS8.1地震震中以南地区的地壳均衡负异常大约为-100 mGal(10-5m·s-2),但其北部的喜马拉雅山脉地区的地壳均衡正异常却达到300~400 mGal.尼泊尔MS8.1地震发生在地壳均衡负异常向正异常过渡的高梯度带上.
(3) 尼泊尔MS8.1地震使震中周围地区的地壳整体向南运动,最大值超过1.5 m,分布在震中东南余震较为密集的区域.较大水平位移集中分布在北纬27.5°N—28.5°N,东经84.5°E—86.0°E之间的长方形区域内部.断层面以北的同震垂向位移总体下降,最大降幅超过-0.5 m,同震重力变化总体为正,最大值超过60 μGal(10-8m·s-2);断层面以南的垂向位移总体为正值,最大升幅超过0.7 m,同震重力变化总体为负,最大降幅超过—120 μGal.
(4) 尼泊尔MS8.1地震使“世界屋脊”喜马拉雅山脉产生沉降,最大同震降幅超过-120 mm;由于地幔的黏滞性响应,70年后,尼泊尔MS8.1地震对喜马拉雅山脉最大垂向位移的贡献将达到-180 mm.尼泊尔MS8.1地震使世界最高峰珠穆朗玛峰下降了2~3 mm,可能会被GPS、InSAR等现代大地测量工具检测到.
Bai Z M, Zhang S F, Braitenberg C. 2013. Crustal density structure from 3D gravity modeling beneath Himalaya and Lhasa blocks, Tibet.J.AsianEarthSci., 78: 301-317.
Bollinger L, Sapkota S N, Tapponnier P, et al. 2014. Estimating the return times of great Himalayan earthquakes in eastern Nepal: Evidence from the Patu and Bardibas strands of the Main Frountal Thrust.J.Geophys.Res., 119: 7123-7163.
Chen S, Wang Q S, Zhu Y Q, et al. 2011. Temporal and spatial features of isostasy anomaly using gravitational admittance model at eastern margin of Tibetan Plateau.ChineseJ.Geophys. (in Chinese), 54(1): 22-34.
Dziewonski A M, Anderson D L. 1981. Preliminary reference earth model.Phys.EarthPlanet.Inter., 25(4): 297-356.
Fielding E J, McKenzie D. 2012. Lithospheric flexure in the Sichuan Basin and Longmen Shan at the eastern edge of Tibet.Geophys.Res.Lett., 39(9): doi: 10.1029/2012GL051680.
Fu G Y, Sun W K. 2012. Overall design and specific structures of the computing codes for coseismic deformations on a layered spherical earth.Earthquake(in Chinese), 32(2): 73-87.
Fu Y T, Li J L, Zhou H, et al. 2000. Comments on the effective elastic thickness of continental lithosphere.GeologicalReview(in Chinese), 46(2): 149-159.
Hu M Z, Li J C, Li H, et al. 2015. The lithosphere effective elastic thickness and its tectonic implications in the Northwestern Pacific.Chinese.J.Geophys. (in Chinese), 58(2): 542-555.
Ji C, Wald D J, Helmberger D V. 2002. Source description of the 1999 Hector Mine, California, earthquake; Part I: Wavelet domain inversion theory and resolution analysis.Bull.Seism.Soc.Am., 92(4): 1192-1207.
McKenzie D. 2003. EstimatingTein the presence of internal loads.J.Geophys.Res., 108(B9): doi: 10.1029/2002JB001766.
Okada Y. 1985. Surface deformation due to shear and tensile faults in a half-space.Bull.Seism.Soc.Am., 75(4): 1135-1154.
Shi Y L, Cao J L. 2008. Effective viscosity of China continental lithosphere.EarthScienceFrontiers(in Chinese), 15(3): 82-95.
Steketee J A. 1958. On Volterra′s dislocations in a semi-infinite elastic medium.Can.J.Phys., 36(2): 192-205.
Sun W, Okubo S, Vanicek P. 1996. Global displacements caused by point dislocations in a realistic earth model.J.Geophys.Res., 101(B4): 8561-8577.
Sun W K, Okubo S, Fu G Y, et al. 2009. General formulations of global co-seismic deformations caused by an arbitrary dislocation in a spherically symmetric earth model-applicable to deformed earth surface and space-fixed point.Geophys.J.Int., 177(3): 817-833.
Tanaka T, Okuno J, Okubo S. 2006. A new method for the computation of global viscoelastic post-seismic deformation in a realistic earth model (I)—vertical displacement and gravity variation.Geophys.J.Int., 164(2): 273-289.
Tanaka T, Okuno J, Okubo S. 2007. A new method for the computation of global viscoelastic post-seismic deformation in a realistic earth model (II)—horizontal displacement.Geophys.J.Int., 170(3): 1031-1052.
Thomson D J. 1982. Spectrum estimation and harmonic analysis.ProceedingsoftheIEEE, 70(9): 1055-1096.
Wang Q, You X Y, Wang W Y, et al. 1998. GPS measurement and current crustal movement across the Himalaya.CrustalDeformationandEarthquake(in Chinese), 18(3): 43-50. Watts A B. 2001. Isostasy and Flexure of the Lithosphere. Cambridge: Cambridge University Press.
Yang T, Fu R S, Huang J S. 2012. On the inversion of effective elastic thickness of the lithosphere with Moho relief and topography data.ChineseJ.Geophys. (in Chinese), 55(11):
3671-3680.
Zhang B, Cheng H H, Shi Y L. 2015.Calculation of the co-seismic effect ofMS8.1 earthquake, Apirl 25, 2015, Nepal.ChineseJournalGeophysics,58(5): 1794-1803,doi:10.6038/cjg20150529.
Zhang G Q, Fu G Y, Zhou X, et al. 2015. Retrieve post-seismic gravity changes induced by Sumatra earthquake (Mw9.3) based on the viscoelastic dislocation theory.ChineseJ.Geophys. (in Chinese), 58(5): 1654-1665.
附中文参考文献
陈石, 王谦身, 祝意青等. 2011. 青藏高原东缘重力导纳模型均衡异常时空特征. 地球物理学报, 54(1): 22-34.
付广裕, 孙文科. 2012. 球体位错理论计算程序的总体设计与具体实现. 地震, 32(2): 73-87.
付永涛, 李继亮, 周辉等. 2000. 大陆岩石圈有效弹性厚度研究综述. 地质论评, 46(2): 149-159.
胡敏章, 李建成, 李辉等. 2015. 西北太平洋岩石圈有效弹性厚度及其构造意义. 地球物理学报, 58(2): 542-555.
石耀霖, 曹建玲. 2008. 中国大陆岩石圈等效粘滞系数的计算和讨论. 地学前缘, 15(3): 82-95.
王琪, 游新兆, 王文颖等. 1998. 跨喜马拉雅的GPS观测与地壳形变. 地壳形变与地震, 18(3): 43-50.
杨亭, 傅容珊, 黄金水. 2012. 利用Moho面起伏及地表地形数据反演岩石圈有效弹性厚度的莫霍地形导纳法 (MDDF). 地球物理学报, 55(11): 3671-3680.
张贝, 程惠红, 石耀霖 .2015.2015年4月25日尼泊尔MS8.1大地震的同震效应. 地球物理学报,58(5): 1794-1803,doi: 10.6038/cjg20150529.
张国庆, 付广裕, 周新等. 2015. 利用震后黏弹性位错理论研究苏门答腊地震(Mw9.3)的震后重力变化. 地球物理学报, 58(5): 1654-1665.
(本文编辑 胡素芳)
Gravitational isostasy background and surface deformation response characteristics of the 2015 NepalMS8.1 earthquake
FU Guang-Yu1,2, GAO Shang-Hua1*, ZHANG Guo-Qing1, SHE Ya-Wen1, SUN He-Ping2
1KeyLaboratoryofEarthquakePrediction,InstituteofEarthquakeScience,CEA,Beijing100036,China2StateKeyLaboratoryofGeodesyandEarth′sDynamics,Wuhan430077,China
We studied the gravitational isostasy background and the surface deformation response characteristics of the 2015 NepalMS8.1 earthquake. The results showed that: (1) the lithosphere effective elastic thickness of Indian block, an area south to the epicenter of 2015 NepalMS8.1 earthquake, is about 9 km, and the load comes mainly from the mantle. However, the lithosphere effective elastic thickness of Lhasa block, an area north to the great earthquake, is about 2 km, and the load comes mainly from the tomography. (2) The gravitational isostasy anomalies are about -100 mGal (10-5m·s-2) at area south to the NepalMS8.1 earthquake, while at area north to the earthquake, the values become 300~400 mGal. The NepalMS8.1 earthquake occurred at a high gradient belt where the isostasy varies from negative anomalies to positive anomalies. (3) Due to the NepalMS8.1 earthquake, the earth surface around the epicenter moved southward as a whole. The maximum of the co-seismic horizontal displacements is above 1.5 m, located at the area southeast to the epicenter. At the area north to the epicenter, the co-seismic vertical displacements are negative and the maximum exceeds -0.5 m, the gravity changes are positive and the maximum is above 60 μGal (10-8m·s-2). However, the values at the area south to the epicenter are vice versa. The maximum co-seismic vertical displacements and gravity changes are 0.7 m and -120 μGal respectively. (4) The NepalMS8.1 earthquake made the roof of the world, the Himalayas, decease as a whole, and the maximum decrease magnitude is more than 120 mm. It is expected the Himalayas will continue to decrease because of the relaxation effects of the mantle. The NepalMS8.1 earthquake made Mt. Everest decrease about 2~3 mm, which may be detectable by modern measuring tool such as GPS and InSAR.
The 2015 NepalMS8.1 earthquake; The lithosphere effective elastic thickness; EGM2008 gravitational model; Spherical dislocation theory; The Himalayas
10.6038/cjg20150606.
国家自然科学基金(41461164004;41331066),国家国际科技合作专项(2105DFR21100),地震预测研究所基本科研业务费专项(2013IES010103),大地测量与地球动力学国家重点实验室开放基金(SKLGED2014-4-3-E)资助.
付广裕,男,研究员,主要从事地震位错形变与地壳重力均衡研究.E-mail:fugy@cea-ies.ac.cn
*通讯作者 高尚华,女,副研究员,主要从事地震观测技术与地震位错理论研究.E-mail:gao966@cea-ies.ac.cn
10.6038/cjg20150606
P315
2015-05-06,2015-06-04收修定稿
付广裕,高尚华,张国庆等. 2015. 2015年尼泊尔MS8.1地震的地壳重力均衡背景与地表形变响应特征.地球物理学报,58(6):1900-1908,
Fu G Y, Gao S H, Zhang G Q, et al. 2015. Gravitational isostasy background and surface deformation response characteristics of the 2015 NepalMS8.1 earthquake.ChineseJ.Geophys. (in Chinese),58(6):1900-1908,doi:10.6038/cjg20150606.

