大连市旅游交通线网优化

于丽莎，杜 红，谢新连

（大连海事大学 交通运输管理学院，辽宁 大连 116026）

1 引言

旅游业作为朝阳行业已成为许多城市的“支柱产业”和“新的经济增长点”，城市旅游的地位和作用越来越突出，与此同时，随着旅游需求的增加，如何合理地优化城市旅游交通线网以解决旅客量迅速增长所引发的旅游交通需求，是目前各大旅游城市关注的重点问题[1]，因此，城市旅游交通规划引起了许多学者的关注[2-4]。但目前对旅游交通的研究主要集中在旅游交通理论、旅游交通管理及发展对策等方面，对城市旅游交通优化模型的研究几乎没有。为此，本文设计并建立一个城市旅游交通线网优化模型，并以大连市为例，研究证明模型具有可行性和有效性，可以为其他城市旅游交通线网优化提供借鉴和参考。

大连市依山傍水、风景秀丽，是具有代表性的旅游城市之一，下辖六区三市一县，拥有丰富且品质较高的旅游资源，现有国家4A 级及以上旅游景点8 个、国家级森林公园6 个和国家级自然保护区4个，省市级风景名胜区、自然保护区和文物保护单位也有多处[5]。目前市区内有百余条公交路线，一条旅游专线。大连市市区旅游专线的线路比较单一，以观光为主，各种旅游资源整合观光的科学性不强。旅游专线对大连市旅游业的发展起到了一定的促进作用，但是其积极作用未得到应有的发挥，整体来看，大连市旅游交通没有形成系统网络、通达度不够，安全和舒适性也得不到保证。因此，合理优化大连市旅游交通线网，对大连市旅游业的发展有着重要意义。

2 旅游交通线网优化模型

2.1 问题描述

旅游交通线网优化就是在对旅游规划地的旅游交通发展历史、现状和未来进行调查、分析和预测的基础上，针对旅游线路现实和潜在的市场需求并适应旅游发展对交通运输的要求，编制旅游线路未来发展的蓝图。大连市市区旅游交通线网规划要结合市区的特点，根据市区旅游景点地理位置、旅游景点客流量以及旅游客运量信息，遵循全面覆盖、经济效益、市场导向、兼顾“冷热”和主体特色的原则，因地制宜地进行规划设计。

本文选取了大连市域内劳动公园（2）、人民广场（3）、会展中心（4）、星海公园（5）、星海广场（6）、金沙滩（7）、森林动物园（8）、付家庄公园（9）、燕窝岭婚庆公园（10）、北大桥（11）、老虎滩海洋公园（12）、俄罗斯风情街（13）、海之韵公园（14）共13个景点及火车站（1）作为旅游交通线网的站点，为表达方便，对各站点进行了编号。

初步拟定可行旅游客运班线共10 条，见表1。在确定可行班线时，充分考虑了各旅游景点的地理位置及客流的分布情况，可以确定拟定的班线中包含线网最优班线。为了方便管理，假设同一条旅游客运班线每天发车班次数是相同的，并且，在同一条旅游客运班线上经营的班车的型号、规格以及载客能力也是相同的。

表1 可行旅游班线集

2.2 数学优化模型

旅游交通线网优化设计追求的总目标是在尽可能全面满足大连市各旅游景点的游客运输需求的基础上，追求运输总效益最好。建立数学模型如下[6]：

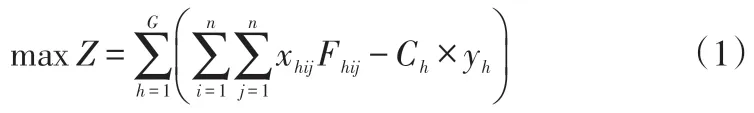
约束条件：

式中：Z为目标函数，表示旅游交通线网每天的营运利润；xhij为决策变量，表示h班线上i,j两站点之间每天完成的游客运输量；yh为整数决策变量，表示h班线每天发车的班次数；Fhij表示h班线上i,j两站点之间的运价；Ch为h班线上班车运行一个往返班次的总成本，包括固定成本和可变成本；Vij为预测或确定的i,j两站点之间每天的客运需求量；n为旅游客运班线站点总数；nh为h班线上站点总数；PPh为h班线上行站点编号的集合；PDh为h班线下行站点编号的集合；APhr为h班线上行前r个站点编号的集合，DPhr为集合APhr在集合PPh中的补集，即PPh=APhr∪DPhr，r=1，2，…，nh-1；ADhr为h班线下行前r个站点编号的集合，DDhr为集合ADhr在集合PDh中的补集，即PDh=ADhr∪DDhr，r=1，2，…，nh-1；θh为h 班线上班车平均载客率（0≤θh≤1）；CAh为h班线上运营班车的单车最大载客人数。

对于车辆运行往返班次总成本Ch，可以采用式（7）计算[7]：

式（7）中：Dh表示h 班线上的车辆每天均摊的折旧费；Wh表示h班线上的车辆每天均摊的维修费；dh表示h班线上一辆车每天可以完成的往返班次数；FOh表示h班线上的车辆一个往返班次所消耗的燃油费；FGh表示h班线上的车辆一个往返班次所分担的管理费用以及其他费用。

上述优化模型中，式（2）为游客需求量约束，所有旅游客运班线从i站点运往j站点的旅客总量不能超过i,j两站点间每天的客运需求量Vij；式（3）和式（4）分别为每一站点正反两方向运输时班车游客承载量约束，班车在任何站点上（下）完游客驶向下一个站点时，车上所载游客总量不能超过其客运承载量（单车最大载客人数与平均载客率之积）；式（5）和式（6）是决策变量的非负约束。式（1）-式（6）就构成了一个完整的混合整数规划模型，既可以实现可行路线的优选，又能求出各旅游班车路线每天的最优发车班次数。

3 优化计算及结果分析

3.1 变量处理

用式（1）-式（6）求解旅游交通线网问题，在形式上，共有G×n2+G=1 970 个变量，包括整数变量G 个，即10 个；有即282个约束条件。

通过分析可以看出，模型中有些变量和约束条件没有实际意义，例如，当i=j时，xhij表示每个站点向本站点运输游客的变量，Vij表示每个站点到本站点的游客运输需求量。在运用混合整数规划方法求解模型之前，可以选择如下两种方式对这些变量和约束条件进行处理：

（1）在确定模型的计算参数时，对h班线上不能够停靠的站点对（i，j），可以采取预先设定Fhij为一个适当负值的方法，从而保证在求得的最优解中，h 班线上（i，j）站点对间无运量发生，即xhij=0；在约束条件（2）中，对于所有班线都不能停靠的站点对（i，j），令Vij=0；

（2）从模型中将这些变量和约束条件消除。

本文将采用第二种处理方式进行求解。根据上述分析，可以消除的变量包括：xhij（h=1，2，…，G；i=j）和xhij（h=1，2，…，G；i或j不是h线上的站点）；可以消除的约束条件包括：式（2）中当i=j 时对应的约束条件和（i，j）不是任何线路上的站点对时所对应的约束条件。本算例中，消除这类变量和约束条件后，有效变量为302 个，有效约束条件为222 个。消除这些变量和约束条件后，可以大大提高模型的求解速度。

3.2 计算参数准备

在建立的旅游交通线网优化模型中，有票价Fhij、游客客运需求量Vij、车辆运行一个往返班次的总成本Ch以及车辆单车最大载客量CAh共4 组参数需要作为已知量预先确定。对于票价Fhij，有Fhij=Fhji，并且在本文中相同站点对间的票价相同，与路线无关。各站点对间的票价及通过历史数据分析预测得出的各站点对间的运量需求见表2。按式（7）计算所得各线路上班车一个往返班次的总成本Ch和各线路上营运的班车最大载客量CAh具体见表3。在计算中，各线路的平均载客率θh都取0.8。

3.3 优化结果及分析

根据表1中列出的可选班线，将已知参数代入化简后的旅游交通线网优化数学模型中，用Lingo 编程求解模型，得到的最优旅游客运班线设置方案及对应的每天发车班次数详见表4，最优目标函数值Z为231 172。可以看到，最终有线路1、2、3、4、7、8、10共7条班线被选中。

表2 游客运输需求量（人次/天）及票价（元）

表3 车辆单车运输成本（元/次）与最大载客量（人/辆）

表4 最优旅游客运班线设置方案

作为最优旅游客运班线运输方案示例，表5给出了线路3上各站点间实际发生的客运量。按照表4给出的旅游客运班线方案安排运输，除了部分线路上的个别客运需求以外，基本可以满足表2中给出的各站点对之间的游客运输需求。由此得到的优化方案是仅根据各站点对每天客运需求量确定的各班线发车班次数，而各班线每天具体的发车时间尚需要进一步根据客流分布特征来确定。

表5 旅游客运班线4站点间客运量（人次/天）

从优化结果的形式上来看，本算例具有多个最优解（xhij值），但各最优解的目标函数值（Z 值）及最优客运班线方案（yh值）都相同，参照表4 中最优旅游客运班线设置方案，区别仅在于客运量xhij值不同。显然，如果两站点对之间的票价是一样的，而且班车在没有所有站点都达到满载的情况下，游客可以在不同线路（具有重叠路段）的班车间发生适当转移，这种客流转移的发生并不会改变运输的总收入及总成本，这也是最优解不唯一的原因。这种最优解的多值性也同时表明，通过优化计算设置的旅游客运班线方案对客流在一定范围内的变化具有适应性。

由于大连市所处的沿海风景区整体背景环境的影响，形成了旅游业明显的季节性。旅游旺季与淡季客流量差别较大，一年中90%的游客集中在4-10 月份，尤以7-9 月最为集中。所以，在实际安排运输时也可根据不同月份的旅游客运需求运用式（1）-式（6）来计算各线路合理的发车班次，以更好地满足不同时期的旅游客运需求。

4 结语

旅游交通的便利程度是衡量旅游业发达程度的重要标志，在食、住、行、游、购、娱等旅游活动六大要素中，属于先决条件，对旅游活动能否顺利进行起着决定性的作用。旅游交通线网优化是旅游交通的重要研究内容之一。本文在充分分析大连市旅游资源现状的基础上，通过建立混合整数优化模型对大连市旅游交通线网进行了研究，通过借助Lingo软件求解，给出了最优的旅游班线设置方案，证明了模型的有效性和实用性，也可以为其他城市旅游交通线网优化提供借鉴。

[1]曹鸿雁.基于TOD 模式的蓬莱市旅游交通规划[J].山东大学学报,2011,26(3):215-218.

[2]雷翔.论旅游城市可持续发展的道路交通[J].规划师,2001,17(2):35-39.

[3]张兴平,杨建军,毛必林.杭州市旅客流量的时空分析及旅游交通对策[J].地理学与国土研究,2000,16(2):61-64.

[4]梁业章.桂林旅游交通优化对策研究[J].产业经济,2013,(2):16-17.

[5]肖瑜.大连市旅游资源深度开发利用研究[J].集团经济研究,2007,(3):172-174.

[6]谢新连,王少成,杨秋平,凡亚军.一种公路客运线网优化设计方法[J].大连海事大学学报,2009,35(4):59-62.

[7]王少成,凡亚军,杨秋平,谢新连.大连市域内公路长途客运主要班车线网优化研究[J].公路,2009,(10):171-175.