云计算环境下基于改进离散粒子群的并行调度算法*

徐华　张庭

(江南大学 物联网工程学院, 江苏 无锡 214122)

云计算环境下基于改进离散粒子群的并行调度算法*

徐华张庭

(江南大学 物联网工程学院, 江苏 无锡 214122)

摘要：针对云计算环境下的任务调度优化问题和传统离散粒子群优化(DPSO)算法早熟、精度低等缺点,提出了一种适合云计算环境下动态调整惯性权重因子的方法,并给出了云计算环境下改进后的离散粒子群优化算法.该算法能快速确定合适的并行任务分配方案,使其达到调度长度最短的优化目标.仿真结果表明:文中改进的DPSO算法的收敛性、前期全局搜索和后期局部探索性能均优于传统的DPSO算法和遗传算法;在任务数较大的情况下,采用改进DPSO算法的并行任务调度算法的调度长度明显优于采用传统DPSO算法和遗传算法的并行任务调度算法.

关键词：云计算;并行算法;离散粒子群优化

随着系统虚拟化和网络技术的发展,云计算已经成为一种新的计算平台.云计算作为一种新兴的并行计算技术,是分布式计算、网格计算和并行计算等计算机技术的商业实现,从其诞生开始就具有巨大的商机[1-2].云计算的主要目的是为了更好地利用分布式资源和解决大规模计算问题.在“云”中如何对任务进行高效合理的调度,实现系统全局最优化,成为云计算研究的重点与难点[3].

一般来说,云计算可以分为3种主要类型的服务:基础设施、平台和软件,这些服务可以通过网页浏览器和移动应用等云客户端进行访问[4].云计算的透明性、可扩展性、冗余性、可用性和经济性使得任务调度的地位更重要[5-6].

在云计算环境中,任务调度是一个NP完全问题[7],其主要目的是优化总调度长度.目前,求解NP完全问题的主要智能优化算法有模拟退火算法、遗传算法和粒子群算法等.并行任务调度是指将任务分成更多、更小的子任务,并将资源分配给这些符合条件的子任务使用,没有依赖关系的子任务可以并行执行.云计算环境下任务量和资源量是非常庞大的,系统时刻都在处理着海量的任务.考虑到大量的任务是在分散的地理资源上执行,因此云计算环境下高效的任务调度算法的设计与实现是一个具有挑战性的问题.

针对传统离散粒子群优化(DPSO)算法早熟、精度低等缺点,文中提出了一种适合云计算并行任务调度的改进离散粒子群优化算法,并通过实验分析该改进离散粒子群优化算法的前期全局搜索和后期局部探索能力、收敛性能.

1云计算并行任务调度数学模型

云计算并行任务调度是指将N个任务通过某种调度策略调度到R个资源上并行执行,使调度长度最短.其中,N个任务可以分为S个子任务,T={T1,T2,…,TN}表示任务集,r={r1,r2,…,rR}表示资源集.Tsub是一个S×N的矩阵,表示任务与子任务之间的依赖关系,第i个任务的第j个子任务Tsub,ij(i=1,2,…,N;j=1,2,…,S)没完成之前,第k(k>j)个子任务Tsub,ik(k=1,2,…,S)不能执行.

在并行执行过程中,te是一个R×S的矩阵,其元素te,p j表示第j(j=1,2,…,S)个子任务在资源rp(p=1,2,…,R)上的执行时间,

临时资源池st是一个S×6的矩阵,它总是存放正在执行或即将执行的子任务.st中第1至第6列分别表示资源集合、执行的子任务集合、执行对应资源的任务数量集合、任务集合、子任务在任务中的位置集合、任务执行时间集合.每个子任务只能在一个资源上执行;一个资源上如果有一个子任务在执行,则该资源不再接受其他子任务.ts,i为任务Ti执行的起始时刻,tex,pi(p=1,2,…,R;i=1,2,…,N)为Ti在资源rp上执行完成的时刻,tpi=max(tex,pi-ts,i),则tpi为任务Ti在资源rp上执行所需的时间.优化目标是使tpi最小.

2并行任务调度算法

2.1　粒子编码与解码

采用DPSO算法求解任务调度问题的关键是建立有效的粒子编码结构,粒子编码可以采用直接编码和间接编码方式.文中采用间接编码方式对每个子任务占用的资源进行编码,编码长度为子任务的个数,这样一个编码对应着一个并行任务调度策略,通过对粒子解码产生调度方案.

2.2　适应度函数

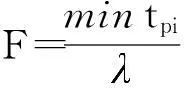
2.3　离散粒子群优化算法

PSO算法是一种随机优化算法,它源于对鸟群捕食行为的研究[8].在粒子群优化算法中,粒子m在进化的过程中有两个向量,分别是位置向量xm=[xm,1,xm,2,…,xm,D]和速度向量vm=[vm,1,vm,2,…,vm,D],其中D为求解问题的维度.粒子的速度决定了粒子运动的方向和速率,位置代表了粒子解在解空间中的位置.PSO算法适用于计算连续的搜索空间,故其研究也主要集中在连续函数方面.然而许多实际工程应用问题是离散的,变量也是有限的,为了使PSO算法能够解决离散优化问题,Kennedy等[9]提出了离散二进制粒子群优化(BPSO)算法.在BPSO算法中,一个二进制空间表示为一个超立方体,每个粒子用一个二进制变量来表示,通过变量的某些位在0或1之间的变化来实现粒子的移动.之后BPSO算法广泛应用于离散优化问题,如经济规划、图形图像、旅行商问题、背包问题和工作流调度问题等[10-15].

在云计算环境下,并行任务调度问题是离散优化问题,将DPSO算法应用到并行任务调度中,数学中的加、减、乘、除运算不再适用,需要重新定义.在DPSO算法中,粒子的位置为一个S维向量,表示为x=[x1,x2,…,xj,…,xS],粒子的速度被定义为粒子位置改变的概率,是一个S维向量,表示为v=[v1,v2,…,vj,…,vS],位置与速度的加法运算实现了粒子位置的移动,即粒子进入新的位置.

云计算环境下位置减去位置等于速度,速度加速度等于速度,位置加速度等于位置,μ(μ∈R)乘以速度等于速度.

求解云计算并行任务调度问题有如下操作：

(1)假设粒子的位置为x,置换序列(f,g)的操作为交换x中的第f和第g个元素.

(2)加法算子(⊕)分为速度和速度相加、位置和速度相加.速度和速度相加表示把后一个速度的置换序列依次加入到前一个置换序列列表的结尾.如A=(1,9,3,7,5,6)⊕(3,5)=(1,9,5,7,3,6),B=A⊕(1,6)=(1,9,5,7,3,6)⊕(1,6)=(6,9,5,7,3,1).

(3)减法算子(-)在云计算环境下只有1种情况,即全局最优解或者个体最优解位置减去个体位置,结果为置换序列.如A=(3,1,2,4,5,6),B=(1,2,4,3,6,5),那么A-B=(4,1,2,3,6,5).

(4)乘法算子(⊗)在云计算环境下只有1种情况,即w(w∈R)与速度相乘,表示以概率w保留粒子的速度.

根据上面的操作,在云计算环境下粒子i的速度和位置更新公式为

vt+1=w⊗vt⊕c1⊗(Pm,t-Pt)⊕c2⊗(Pg,t-Pt)

(1)

xt+1=xt⊕w⊗vt+1

(2)

式中,w为惯性权重,Pm,t为个体当前最优值,Pg,t为全局当前最优值,Pt为粒子的当前位置,c1、c2为学习因子.

随机产生粒子种群的初始位置和速度,然后按照式(1)和(2)进行迭代,直到满足终止条件为止,此时的全局最优值就是优化运算后的近似最优解.

2.4　惯性权重的调整

惯性权重w是粒子群算法中很重要的一个参数,它平衡了粒子群体的全局搜索能力和局部探索能力.为了使算法在初期能进行较强的全局搜索、而在后期进行较强的局部搜索,文中采用指数增长的惯性权重计算公式,即

(3)

式中:K=wmax-wmin,wmax和wmin分别为惯性权重的最大值、最小值;M=I/Imax,I为当前迭代次数,Imax为最大迭代次数;a(a∈[0.6,1.2])、b(b∈[10,25])为调节因子.调节因子a和b的取值由经验决定,经过a、b的调整,随着进化次数的增加,惯性权重w加速减小,前期有利于全局搜索,后期有利于局部探索.

2.5　算法流程图

文中提出的改进离散粒子群优化算法的流程图如图1所示.

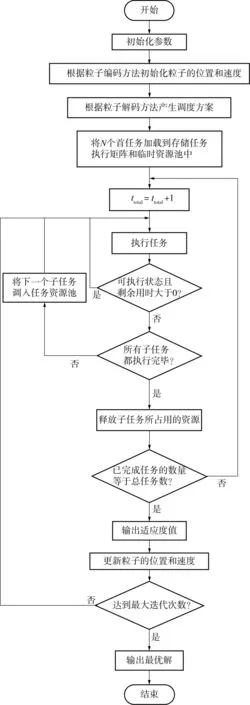
图1　文中算法流程图Fig.1　Flowchart of the proposed algorithm

3仿真实验

为测试文中算法在云计算任务调度中的应用效果,采用CloudSim平台进行测试,在Matlab 2012中进行仿真.本实验的硬件环境为:内存8 GB,硬盘500 GB;软件环境为:Windows 7操作系统,Eclipse kepler开发工具.模拟仿真了8个虚拟资源、40个不同的子任务,在相同的实验条件下对传统DPSO算法[8]、遗传算法[16]和文中算法的性能进行比较与分析.实验参数设置如下:种群规模为500,最大迭代次数为400,惯性权重最大值和最小值分别为0.96、0.36,学习因子c1=0.1、c2=0.3.

在不同迭代次数下反复进行50次实验,并对实验结果取平均值,结果如表1所示.从表中可以看出:文中算法在求解并行任务调度问题时,找到的最优解远远小于DPSO算法和遗传算法,且其最优解精度分别比DPSO算法、遗传算法提高了2.96%、6.65%;对于最优解中的最差解,文中算法略大于DPSO算法和遗传算法,表明文中算法的全局搜索能力强于DPSO算法和遗传算法;文中算法找到最优解的平均迭代次数大于其他两种算法,表明文中算法有较好的收敛性能.

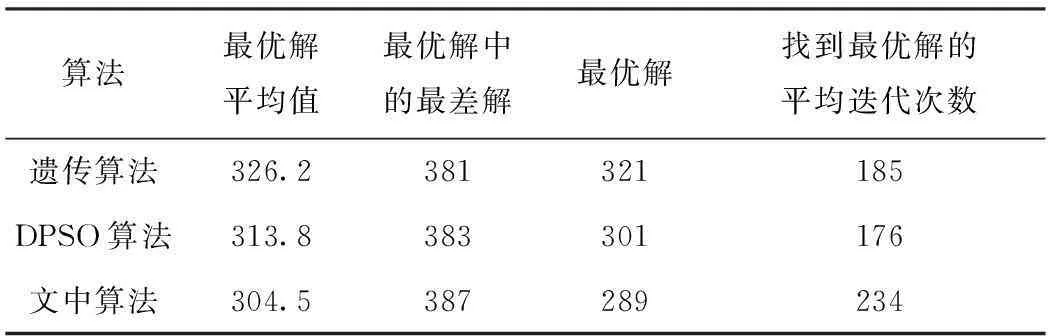
表1　3种算法的实验结果比较Table 1　Comparison of experimental results among three algorithms

为进一步分析文中算法的全局搜索能力和收敛性特性,对文中算法和传统DPSO算法在400次迭代过程中的任务调度长度进行仿真,结果如图2所示.

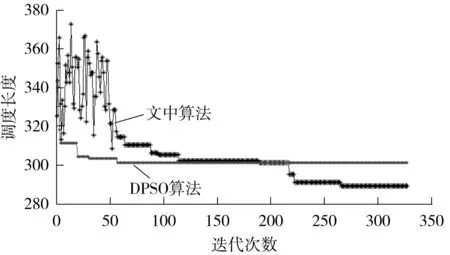
图2　不同迭代次数下两种算法的调度长度对比Fig.2　Comparison of scheduling length between two algorithms under different iteration times

从图中可以看出,传统DPSO算法因只重视总完成时间而造成了一些潜在的优良粒子丢失,很快陷入局部极优,进入收敛状态,并最终收敛于最优解301.文中改进算法在迭代次数小于50时,粒子一直处于搜索状态,多次跳出局部极优,这表明文中算法在迭代前期具有较强的全局搜索能力;在此之后粒子慢慢局部探索,逐步寻找到全局最优解,与传统DPSO算法相比,文中算法在迭代后期具有较强的局部探索性能.文中改进算法在迭代50次时,粒子开始收敛,最终靠近全局最优解289.表1和图2表明,文中算法的收敛性、全局探索能力和局部探索能力圴优于传统DPSO算法和遗传算法.

文中算法、传统DPSO算法和遗传算法在不同任务数量(20、40、60、80、100)下的适应度如图3所示.从图中可以看出,在任务数量较小的情况下,3种算法的适应度差别并不明显,但随着任务的增多,文中算法的调度长度明显优于其他两种算法,并且任务越多这个趋势越明显.

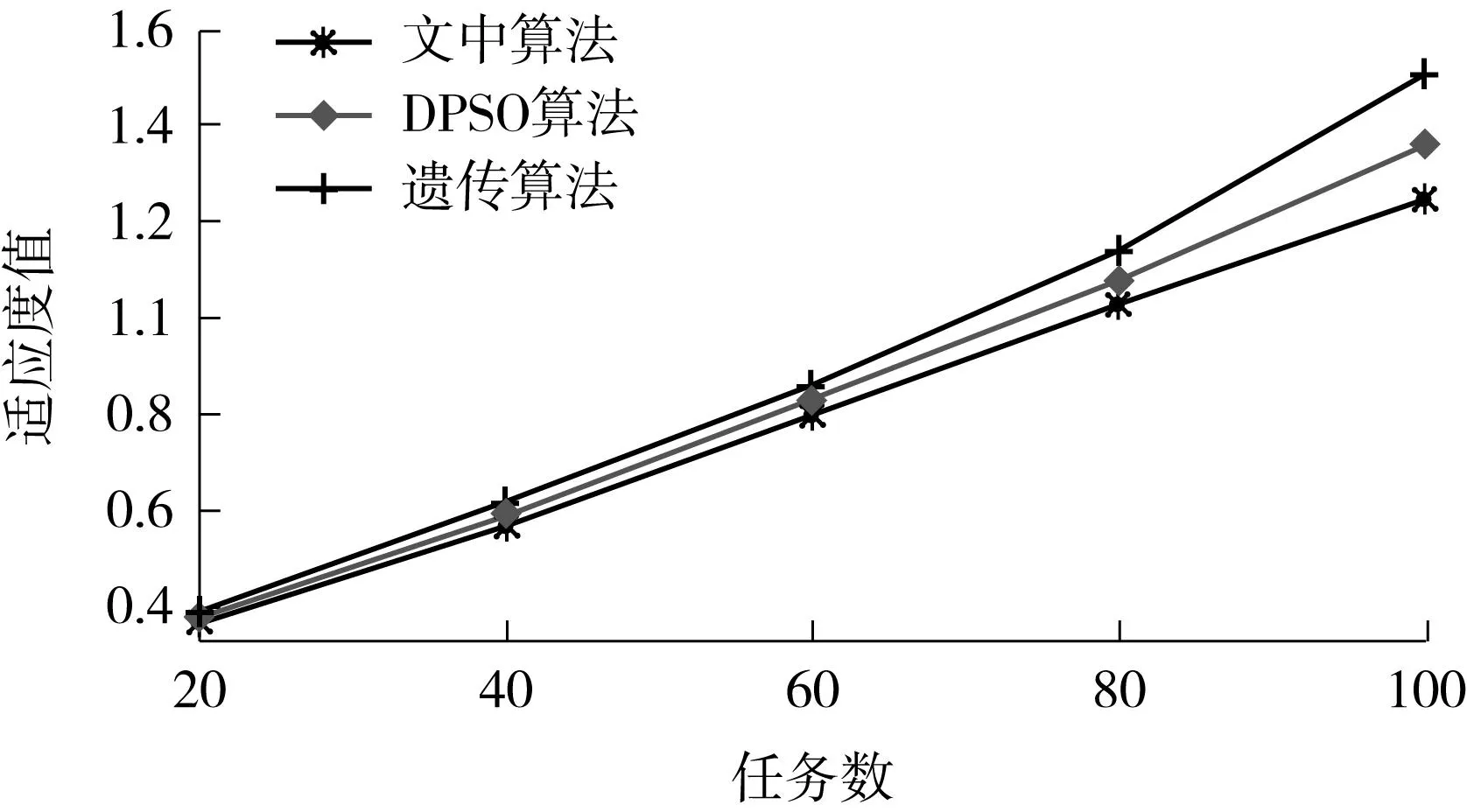
图3　3种算法在不同任务数下的适应度值Fig.3　Fitness values of three algorithms with different numbers of tasks

4结论

文中提出了一种适用于云计算环境下的并行任务调度算法,首先定义了云计算环境下的并行任务调度数学模型,然后进行粒子的编码与解码并定义操作算子,最后采用改进的DPSO算法对任务调度方案进行并行调度迭代寻优.仿真结果表明,文中算法获得的最优解、前期全局搜索能力和后期探索性能均优于传统DPSO算法和遗传算法,并且在迭代后期具有良好的收敛性能.

参考文献:

[1]Sadiku M N O,Musa S M,Momoh O D.Cloud computing:opportunities and challenges [J].IEEE Potentials,2014,33(1):34-36.

[2]Stieninger Mark,Nedbal Dietmar.Characteristics of cloud computing in the business context:a systematic literature review [J].Global Journal of Flexible Systems Management,2014,15(1):59- 68.

[3]董丽丽,黄贲,介军.云计算中基于差分进化算法的任务调度研究 [J].计算机工程与应用,2014,50(5):90-95.

Dong Li-li,Huang Ben,Jie Jun.Task scheduling based on differential evolution algorithm in cloud computing [J]. Computer Engineering and Applications,2014,50(5):90-95.

[4]Chong H Y,Wong J S,Wang X.An explanatory case study on cloud computing applications in the built environment [J].Automation in Construction,2014,44:152-162.

[5]Deng Qian-ni,Chen Quan.Cloud computing and key technology [J].Development & Application of High Perfor-mance Computing,2009,26(1):2- 6.

[6]Lin Weiwei,Liang Chen,James Z,et al.Bandwidth-aware divisible task scheduling for cloud computing [J].Software:Particle and Experience,2014,44(2):163-174.

[7]Arfeen M A,Pawlikowski K,Willig A.A framework for resource allocation strategies in cloud computing environment [C]∥Proceeddings of 2011 IEEE the 35th Annual Computer Software and Applications Conference Workshops.Munich:IEEE,2011:261-266.

[8]Kennedy J,Eberhart R.Particle swarm optimization [C]∥Proceedings of IEEE International Conference on Neural Networks.Piscataway:IEEE,1995:1942-1948.

[9]Kennedy J,Eberhart R.A discrete binary version of the particle swarm algorithm [C]∥Proceedings of the World Multiconference on Systemics,Cybernetics and Informa-tics.Piscataway:IEEE,1997:4104-4109.

[10]Shao X Y,Liu W Q,Liu Q,et al.Hybrid discrete particle swarm optimization for multi-objective flexible job-shop scheduling problem [J].The International Journal of Advanced Manufacturing Technology,2013,67(9/10/ 11/12):2885-2901.

[11]Iman Z,Gerard L,Arindam G.A new technique for optimal allocation and sizing of capacitors and setting of LTC [J].International Journal of Electrical Power & Energy Systems,2013,46:250-257.

[12]Wang Xiao-hua,Mu Ai-qin,Zhu Shi-song.ISPO:a new way to solve traveling salesman problem [J].Intelligent Control and Automation,2013,4(2):122-125.

[13]Amira G,Abdesslem L,Salim C.Solving 0-1 knapsack problems by a discrete binary version of cuckoo search algorithm [J].International Journal of Bio-Inspired Com-putation,2012,4(4):229-236.

[14]Cao J F,Chen J J,Zhao Q S.An optimized scheduling algorithm on a cloud workflow using a discrete particle swarm [J].Cybernetics and Information Technologies,2014,14(1):25-39.

[15]陈自郁,何中市,何静媛.一种求解集合组合问题的离散粒子群优化模型 [J].华南理工大学学报:自然科学版,2010,38(4):141-146.

Chen Zi-yu,He Zhong-shi,He Jing-yuan.Discrete particle swarm optimization model for set-based combinatorial optimization problems [J].Journal of South China University of Technology:Natural Science Edition,2010,38(4):141-146.

[16]Fogel D B.An introduction to simulated evolutionary optimization [J].IEEE Transactions on Neural Networks, 1994,5(1):3-14.

Improved Discrete Particle Swarm-Based Parallel Schedule Algorithm in Cloud Computing Environment

XuHuaZhangTing

(School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, Jiangsu, China)

Abstract:Aiming at the optimization problem of task scheduling in the cloud computing environment and the defects of prematurity and low precision of traditional discrete particle swarm optimization (DPSO) algorithms, a method of dynamically adjusting the inertia weight factor is proposed in a cloud computing environment, and an improved discrete particle swarm optimization algorithm is put forward. This algorithm can determine the appropriate parallel task allocation scheme quickly, and makes the scheme achieve the shortest scheduling length. Simulation results show that the improved DPSO algorithm is superior to the traditional DPSO algorithm and the genetic algorithm in terms of the convergence, the previous global search capability and the late local exploration performance, and that, in the case of a large number of tasks, the parallel task scheduling algorithm using the improved DPSO algorithm is superior to those using the traditional DPSO algorithm or the genetic algorithm in terms of scheduling length.

Key words:cloud computing; parallel algorithms; discrete particle swarm optimization

中图分类号：TP301

doi：10.3969/j.issn.1000-565X.2015.09.015

作者简介：徐华(1978-)，女，博士，副教授，主要从事人工神经网络、模糊系统、水污染等研究.E-mail: joanxh2003@163.com

*基金项目：国家留学基金委资助项目(201308320030)；江苏省自然科学基金资助项目(BK20140165)

收稿日期：2014-09-28

文章编号：1000-565X(2015)09-0095-05

Foundation items： Supported by the National Scholarship Fund Program(201308320030) and the Natural Science Foundation of Jiangsu Province(BK20140165)