基于三重赋权和系统聚类分析法的全国空气污染实证分析

陈迎欣,魏 薇

（哈尔滨工程大学a.经济管理学院；b.灾难与危机管理研究所，哈尔滨 150001）

0 引言

随着雾霾问题的层层升级，空气污染评价、防治与治理问题亟待解决。目前国内外经典的空气质量评价方法主要有API指数评价法[1]，单因子指数法[2]，模糊综合评价法[3]、美国橡树岭大气质量指数法[4]、白勃考大气污染综合指数[5]、格林大气污染综合指数法[6]等。此外，国内外学者多角度对空气质量进行了研究。

以往对空气质量的研究大多在已有的方法或模型上进行特定类型区域的个别案例研究，或者对环境与经济之间的关系进行研究，而且对于污染物的研究趋于复杂化，很少有人对包括数据的处理，权重的确定等评价方法本身入手，缺少应用简洁的方式对大范围地区空气质量进行归类研究。本文通过运用一种基于德尔菲法、均方差法和极差法的新型综合赋权方法建立模型，有机结合了每种算法的优势，对我国31个省市空气质量进行综合评价，根据废气中二氧化硫、氮氧化物以及烟尘粉尘三种污染物的情况，应用系统聚类中Q-型聚类分析方法，对31个省市进行全面分类，针对不同类型地区提出了相应建议和解决办法。并且应用系统聚类中R-型聚类分析方法对废气中二氧化硫、氮氧化物以及烟尘粉尘三种污染物进行类别划分，基于同一类别中元素的特性是相同或类似的思想，提出了一种新型的适用于快速评价我国境内某地区空气质量的方法。

1 理论基础与研究假设

1.1 理论基础

由于系统聚类分析法[7]是比较成熟的研究方法，这里不再赘述，下面阐述三重赋权法。目前在多指标综合评价中，应用的最广泛的确定指标属性权重的方法有三类：主观赋权法、客观赋权法及主客观相结合的综合赋权法[8]。

本文采用的三重赋权法是为减少单一主观或客观赋权的弊端，基于德尔菲法[9]、均方差法[10]和极差法[11]的一种新型综合赋权方法，实现了主观赋权法和客观赋权法的有机结合，充分利用各自的优点,使得在进行综合评价的实证中计算出的指标权重值具备较强的实际意义，在评价中有效的减少计算误差。

计算步骤：

(1)先将原始数据经标准化后的数据用德尔菲法的权重值做乘积变换。

(2)用均方差赋权方法求出各个指标权重，并归一化。(3)用极差赋权方法求出各个指标权重，并归一化。(4)在以上三步的基础上，求均方差方法和极差方法求得的权重值的算术平均值，并归一化。

1.2 研究假设

环保专家普遍认为，以重化工业为主的产业结构，包括水泥、钢铁、焦化等生产过程中废气的排放是对资源环境造成的压力主要来源，而以二氧化硫、氮氧化物、烟尘粉尘为首的主要空气污染物排放增加的趋势仍然在延续[12]，因此，本文提出如下假设：

(1)不考虑其他环境因素，空气污染完全由空气中废气排放过度引起；

(2)不考虑其他污染物，废气中的污染物由二氧化硫、氮氧化物、烟尘粉尘组成；

(3)空气质量对空气污染天气起决定性作用；

(4)不考虑各地区间污染物的扩散。

2 研究方法及研究结果

2.1 空气质量综合评价模型的建立

根据问题的分析及模型假设，查阅了《中国统计年鉴》中历年资源与环境资料，选取了2011年度31个省市废气中主要污染物的排放情况数据(单位：万吨)，如表1所示。对31个省市空气质量进行综合评价，并且根据废气中污染物的构成情况对各地区进行分类，找出同类型地区，以便进行空气治理。

基于三重赋权法建立模型如下：

其中：Sj为 j地区空气质量的综合得分；aji为 j地区i指标标准化后数据；W=(b1，b2，b3)为各地区的权重向量，bi为三个指标的权重值，由三重赋权法求得；i为空气污染物指标，依次为二氧化硫、氮氧化物、烟尘粉尘；j为地区，j=1，2，…，31，依次为北京、天津、河北、山西、内蒙古、辽宁、吉林、黑龙江、上海、江苏、浙江、安徽、福建、江西、山东、河南、湖北、湖南、广东、广西、海南、重庆、四川、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆，以上地区包含了中国大陆所有省份和直辖市以及自治区。

原始数据矩阵为

德尔菲法为主观赋权法的一种，由学者和环保专家的经验共同得出，其权重向量为：

根据(8)式至(11)式，归一化后可计算出基于均方差赋权法的最终权重值，经MATLAB编程计算求得，各指标综合权重向量如下：

根据(11)式至(13)式，归一化后可计算出基于极差赋权法的最终权重值，经MATLAB编程计算求得，各指标综合权重向量如下：

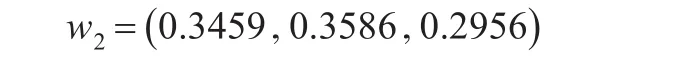
综上，根据计算步骤(4)，基于德尔菲法、均方差法和极差法的三重赋权法的最终权重向量为：

三个指标依次为二氧化硫、氮氧化物、烟尘粉尘，指标权重向量代表各个指标在空气质量综合评价中所占比重。

2.2 空气质量综合评价模型的实证结果

31个省市的空气质量综合评分根据(1)式，由各指标的标准化后对应数据与对应权重值的乘积取得。并根据各地区的污染物的构成情况应用SPSS软件对地区进行分类，见表1所示。

3 评价结果SPSS聚类分析

运用SPSS进行聚类分析的方法有两步聚类、K均值聚类以及系统聚类。两步聚类能够同时处理分类变量和连续变量，继而有效分析具有复杂类别结构的海量数据的大样本，聚类个数既可以自己指定，也可以系统自动选择。K均值聚类法适用于样本数据量较大且分类数目确定的聚类分析。系统聚类要求样本数据量较小且无异常值的聚类分析[13]。本文选取全国31个省市的3种空气污染物的排放量为研究对象，数据量较小，且分类数目未知，故本文应用系统聚类法进行分析。

根据对象不同，系统聚类分析既可以对样本进行分类（Q-型聚类分析[14]），又可以对指标进行分类（R-型聚类分析[15]）。在本文中对31个省市的环境空气类别进行分类时，选用Q-型聚类分析，对二氧化硫、氮氧化物和烟尘粉尘三种指标进行分类的时，选用R-型聚类分析。

表1 31个省市空气污染物排放数据及空气质量评价表

基于样本数据使用SPSS软件，在方法和距离的选用上分别采取类间平均链锁法和相关系数距离，运行结果如表2，表3，图1，图2所示。

表2 案例处理汇总表

由表2可知，31个样本完全有效，有效率为100%，无缺失；

从图1系统聚类分析树状图可见，按空气污染情况的差异本文选取的我国31个省市可分成四类。如表3所示。

表3 聚类结果表

31个省市的空气质量评分以及聚类结果如表1和表3所示。综合评分越高的地区，空气污染越严重。根据各地区空气中污染物的构成情况和评分情况，将各地区的环境空气类别划分为A、B、C、D四类，分别为轻度污染、中轻度污染、中度污染、重度污染。

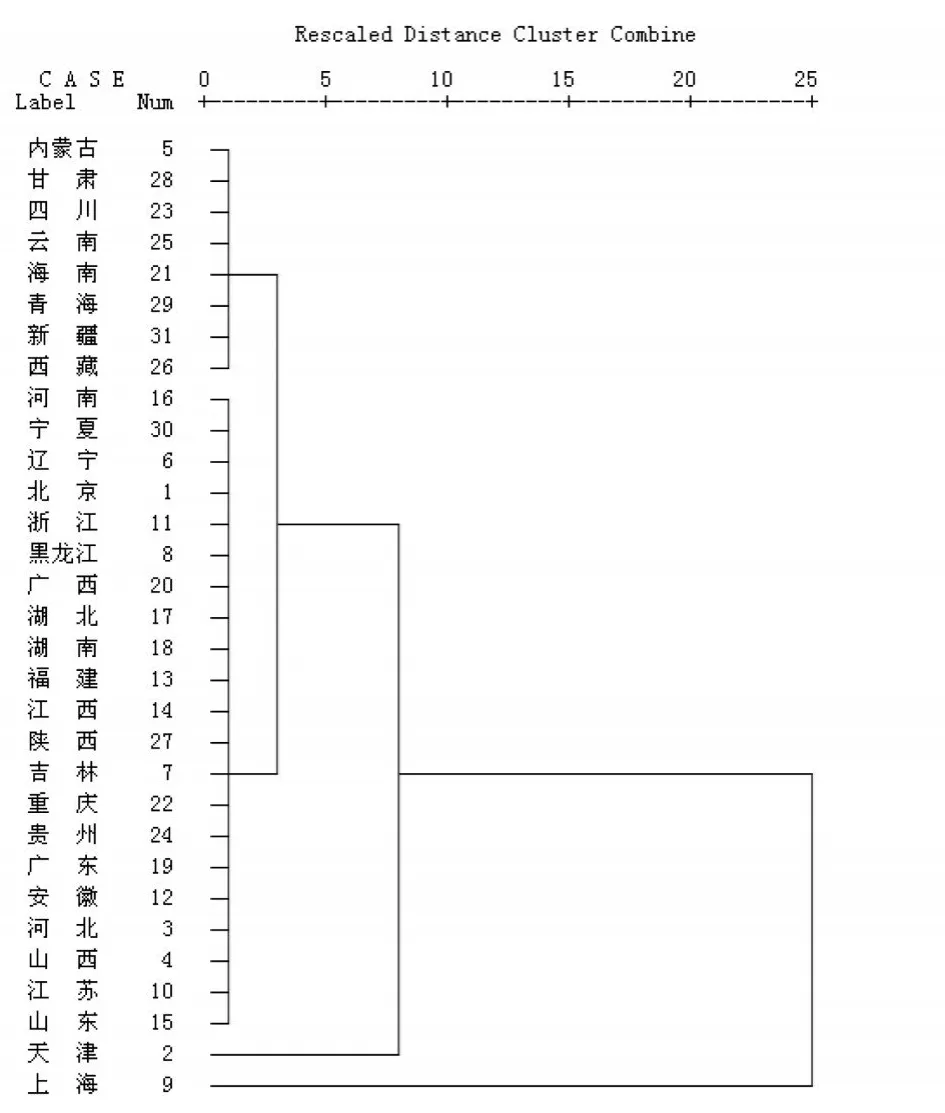
图1 SPSS系统聚类分析树状图

根据全国各地区的空气污染情况以及聚类分析的方法，将各地区按污染轻重划分为四类，其城市类型、发展战略以及预期目标如表4所示。

表4 全国各地区发展水平与空气环境类型分析

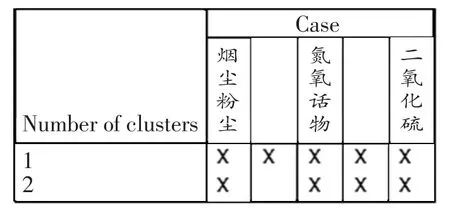
图2 冰柱聚类图

图2是对二氧化氮、烟尘粉尘和氮氧化物三种指标进行聚类的冰柱图，可以直观的看出，当将指标划分成两类的时候，氮氧化物与二氧化硫先聚合。这表明在评价本文31个省市空气污染状况的时候，可在氮氧化物和二氧化硫两个指标中选择一个，再加上烟尘粉尘即可。氮氧化物和二氧化硫在其中的作用是基本等价的。在氮氧化物和二氧化硫中选择一个典型的代表性指标的方法应遵循公式(14)，选取该类中相关指数的平均值Rˉ2最大者。

其中k为该类变量个数，rij为该类内变量xi对类中其它变量的相关系数。

表5 相似性矩阵表

根据(14)式与表5，二氧化硫对氮氧化物的相关系数与氮氧化物的相似系数相等。

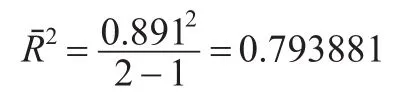
显然，选择氮氧化物或二氧化硫作为代表性指标的意义是等同的，应根据当地的实际情况而定。

4 结论

结果表明，所研究地区的空气污染与经济发展情况基本符合库兹涅茨环境污染的倒U型曲线的变化特征，即在城市化和工业化的进程中，空气污染的程度首先随人均GDP的增长而增加，当人均GDP的增长进一步加强，且到达一定临水平时，空气污染程度会显示下降趋势。上海、天津、北京和重庆，作为特大型城市，空气质量排名居于中下游,空气污染严重。位于西南西北地区的西藏、青海、新疆、甘肃、内蒙古、海南、四川、云南空气质量良好的。

目前我国实行的空气质量评价体系和数据检测系统尚不完善，因此对于各地区空气质量的排名和预测结果不够严谨。2012年起有多个试点采用新的空气质量评价体系，API监测的污染物比原有的标准增加了O3、CO、PM2.5三项，评价办法也变为从当天的0时至24时。新的空气质量评价标准正在逐步分期实施，根据环保部要求，2016年全面实施新标准，将为全面衡量各地区的小时空气质量、日空气质量以及对区域空气质量长期预测提供合理有效的依据。

[1]李小飞,张明军,王圣杰等.中国空气污染指数变化特征及影响因素分析[J].环境科学,2012,33(006).

[2]朱灵峰,王燕,王阳阳等.基于单因子指数法的海浪河水质评价[J].江苏农业科学,2012,40(3).

[3]王秀.模糊综合评价法在环境空气质量评价中的应用[J].环境保护与循环经济,2012，(12).

[4]Norby R J,Cotrufo M F.Global Change:A Question of Litter Quality[J].Nature,1998,396(6706).

[5]Schneider A M.An Effluent Fee Schedule for Air Pollutants Based on Pindex[J].Journal of the Air Pollution Control Association,1973,23(6).

[6]妙旭华.天水市环境空气质量评价与分析[J].甘肃科技,2011,27(19).

[7]Corpet F.Multiple Sequence Alignment with Hierarchical Clustering[J].Nucleic Acids Research,1988,16(22).

[8]陈国铁.我国企业生态化建设研究[D].福建师范大学,2009.

[9]袁勤俭,宗乾进,沈洪洲.德尔菲法在我国的发展及应用研究——南京大学知识图谱研究组系列论文[J].现代情报,2011,31(5).

[10]斯蔼,杜关记,王爽,等.基于均方差-模糊综合评判复合模型的地下水水质评价[J].地下水,2009,31(1).

[11]巫业山.测量不确定度A类评定的两种方法:贝塞尔法和极差法[J].衡器,2011,40(4).

[12]于鲁冀,青彩华,章显.基于主要污染物新增量的排污权指标来源研究[J].环境科技,2013(1).

[13]于秀林,数理统计,任雪松等.多元统计分析[M].北京：中国统计出版社,1999.

[14]黄学良,许礼刚.Q型聚类分析法在城市经济空间分区中的应用研究[J].广东交通职业技术学院学报,2006.

[15]潘俊,冷特.R型聚类对辽河不同断面水质指标相关性分析[J].环境科学与技术,2012.