关于增量极限学习机的逼近阶估计

崔新月，王 博，张 瑞，吕晓丽

(西北大学 数学学院, 陕西 西安 710127)



·数理科学·

关于增量极限学习机的逼近阶估计

崔新月，王 博，张 瑞，吕晓丽

(西北大学 数学学院, 陕西 西安 710127)

增量极限学习机;贪婪算法;字典集;逼近阶

近年来,人工神经网络已成功应用于自动控制、模式识别、机械工程以及生物医学等领域中,其中单隐层前向神经网络(Single-Hidden layer feedforward networks,SLFNs)由于结构简单、学习能力强、能解决传统学习算法无法解决的问题等特性,是目前为止研究最为广泛的一类神经网络模型。虽然著名的万有逼近定理[1-3]已经表明,通过适当调整网络中的所有参数单隐层前向神经网络能够以任意精度逼近一个给定的连续目标函数,但传统的神经网络学习算法往往是基于梯度下降法而设计的,因而具有学习速度慢、容易陷入局部最小、需要人为调整网络参数等不足。

极限学习机(Extreme learning machine,ELM)[4]是近年来提出的一种简单而高效的学习算法。其基本思想是通过随机机制来固定一个学习系统的隐变量将其化为线性系统, 从而大大提高学习速度并保证泛化能力,与传统的神经网络学习算法相比,极限学习机具有如下特点：①具有更快的学习速度和更强的泛化能力； ②结构简单,并且可以避免陷入局部最小和过度拟合等问题；③所适用的激活函数范围较广,既可以是连续的激活函数类,也可以是不连续的激活函数类；④不仅算法中所选取的隐节点参数之间相互独立,而且参数选取与训练集也是独立的。文献[4]中证明了当隐层激活函数无限可微且网络中的输入权重和隐层阈值服从某种连续概率分布随机选取时, 该算法能以任意小的误差来逼近给定的连续目标函数。

在极限学习机中,唯一需要人为调整的参数就是隐单元个数。在原始极限学习机中,隐单元个数是采用多次人工实验比较误差的方法确定的,但这种选取方法造成了很大的工作量,不仅很耗时而且最终确定的隐单元个数无法保证是最优的。网络结构直接影响其泛化能力,具体地说,当隐单元个数较少时会导致训练误差大且泛化能力差;当隐单元过多时虽然会减小训练误差,但其泛化能力仍然较差。基于这一问题，文献[5]进一步提出了网络结构增长型的极限学习机,即增量极限学习机(Incremental extreme learning machine, I-ELM)。

在增量极限学习机中,无需提前设置隐单元个数,而是通过逐个添加隐单元来逼近给定的目标函数。文献[5]中已经证明了增量极限学习机的全局逼近能力,当可加型隐节点或RBF型隐节点的激活函数g:R→R满足span{g(a,b,x):(a,b)∈Rd×R}在L2中稠密时,由增量极限学习机所生成的网络序列可以以概率1逼近任意给定的连续目标函数。

然而，学习理论的核心问题之一是对学习算法的性能进行量化评估,已有的理论结果只是从定性角度对增量极限学习机的逼近能力进行了分析。本文将从定量角度对增量极限学习机的逼近能力进行具体分析,进而对其快速收敛的本质给出理论保证。

1 增量极限学习机回顾

不失一般性,本文只考虑含有n个隐节点以及一个线性输出节点的单隐层前向神经网络,其数学模型可表示为

其中gi(x)表示第i个隐节点的输出,βi表示连接第i个隐节点与输出节点的输出权重。最常见的两种隐节点类型为

1) 可加型隐节点:gi(x)=g(ai·x+bi),ai∈Rd,bi∈R。其中ai是连接输入层与第i个隐节点的权重向量,bi是第i个隐节点的阈值。

2) RBF型隐节点:gi(x)=g(bi‖x-ai‖),ai∈Rd,bi∈R+。其中ai,bi分别表示第i个RBF型隐节点的中心和影响因子。

增量极限学习机的核心思想是通过逐个增加隐节点来确定最优的网络结构,并且在增加一个新隐节点时,已存在隐节点的输出权重保持不变,只需计算新增隐节点与输出层的连接权重。 其具体的网络产生迭代公式为

fn(x)=fn-1(x)+βngn(x)。

其中fn(x)表示第n步产生的网络,gn(x)是第n步新增隐节点的输出,βn表示连接第n个新增隐节点与输出层的权重,按照下式直接计算可得

limn→∞‖f-fn‖=0

以概率1成立。

引理1表明，当迭代步数n趋于无穷大时,由增量极限学习机所产生的网络序列以概率1无限逼近于给定的目标函数f。

2 增量极限学习机的逼近阶估计

2.1 准备知识

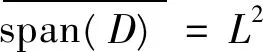
性质1[7]对于可加型隐节点g(a·x+b),若激活函数g:R→R不是多项式函数，则span{g(a·x+b):(a,b)∈Rd×R}在L2中稠密。

性质2[7]对于RBF型隐节点g(b‖x-a‖),若激活函数g:R→R是有界可积的连续函数,则span{g(b‖x-a‖):(a,b)∈Rd×R+}在L2中稠密。

2.2 字典集和目标函数空间的构造

2.3 增量极限学习机的逼近阶

引理2[10]若f∈A1(D*,M),则‖f‖≤M。

‖en‖=‖f-fn‖

成立。

证 明 由于f∈A1(D*),故由A1(D*)的定义可知,必存在一个M0>0，使得f∈A1(D*,M0)。

定义正项数列{bn}:

(1)

其中

则由数学归纳法可以证明

f-fn=en∈A1(D*,bn)。

接下来用数学归纳法证明上述结论。

当n=0时,由假设可知命题显然成立,即e0=f∈A1(D*,b0)。

假设en-1∈A1(D*,bn-1)成立,则有

成立,从而由fn=fn-1+βngn可推得f-fn=f-fn-1-βngn,即

其中,Λ′=Λ∪{n},

而

成立,所以en∈A1(D*,bn)。

综上可知,en∈A1(D*,bn)成立，于是可推得

即

(2)

成立。从而由式(1)可知

(3)

又由于{en}满足

‖en‖2=‖en-1-βngn‖2=

(4)

于是由式(3)，(4)可推得

‖en‖2bn≤

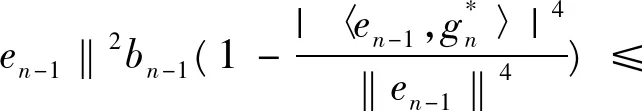
‖en-1‖2bn-1≤

⋮

(5)

又由式(2)可知

(6)

故由式(4)，(6)可知

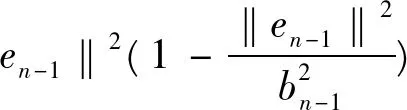
(7)

综合(5)，(7)两式即知

‖en‖6=

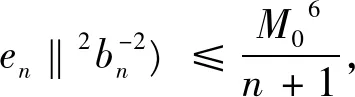
亦即

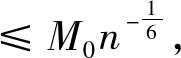
从而证得

‖en‖=‖f-fn‖

定理得证。

注1 这里AB表示存在一个常数C，使得A≤CB。

3 结 语

[1]BARRONAR.Universalapproximationboundsforsuperpositionsofasigmoidalfunction[J].IEEETransactionInformationTheory,1993(39)：930-945.

[2]HORNIKK.Approximatoncapabilitiesofmultilayerfeedforwardnetworks[J].NeuralNetworks,1991(4): 251-257.

[3]PARKJ,SANDBERGIW.Universalapproximationusingradial-basis-functionnetworks[J].NeuralCompute,1991(3): 246-257.

[4]HUANGGB,ZHUQY，SIEWCK.ExtremeLearningMachine:Theoryandapplications[J].Neurocomputing,2006, 70: 489-501.

[5]HUANGGB，LEIChen.UniversalApproximationUsingIncrementalConstructiveFeedforwardNetworksWithRandomHiddenNodes[J].IEEETransactionNeuralNetworks, 2006,17(4)：879-892.

[6]LEVIATAND，TEMLYAKOVVN.Simultaneousapproximationbygreedyalgorithms[J].AdvancedComputeMath, 2006，25：73-90.

[7]HUANGGB，CHENL.Convexincrementalextremelearningmachine[J].Neurocomputing, 2007，70：3056-3062.

[8]DEVORERA，TEMLYAKOVVN.Someremarksongreedyalgorithms[J].AdvancedComputeMath, 1996，5：173-187.

[9]BARRONR,COHENA，RONALDA.Denore.ApproximationAndLearningByGreedyAlgorithms[J].TheAnnalsofStatistics, 2008，36(1)：64-94.

[10]LIVSHITSED.RateofConvergenceofPureGreedyAlgorithms[J].Math.Notes, 2004，76(4)：497-510.

[11]KONYAGINSV，TEMLYAKOVVN.Rateofconvergenceofpuregreedyalgorithms[J].EastJApproximation, 1999，5：493-499.

(编 辑亢小玉)

The approximation order of Incremental extreme learning machine

CUI Xin-yue, WANG Bo, ZHANG Rui, LÜ Xiao-li

(School of Mathematics, Northwest University, Xi′an 710069， China)

Incremental extreme learning machine; greedy algorithm; dictionary; approximation rate

2014-07-11

陕西省自然科学基金资助项目(2014JM1016)

崔新月，女，山西运城人，从事ELMs技术的算法及理论研究。

张瑞，女，陕西西安人，西北大学教授，博士生导师，从事人工神经网络及ELMs技术的研究。

O29

：ADOI：10.16152/j.cnki.xdxbzr.2015-02-001