致密油藏体积压裂直井非稳态压力分析
刘 雄,田昌炳,纪淑红,王 磊
(1.中国石油勘探开发研究院,北京 100083; 2.中国石化石油勘探开发研究院,北京 100083)
致密油藏体积压裂直井非稳态压力分析
刘 雄1,田昌炳1,纪淑红1,王 磊2
(1.中国石油勘探开发研究院,北京 100083; 2.中国石化石油勘探开发研究院,北京 100083)
针对致密油藏开发特征,基于拉式空间变换,建立了直井体积压裂非稳态压力分析模型,并对影响非稳态压力动态传播的相关参数敏感性做了分析。结果表明:整个渗流过程包括6个阶段,即:线性流、复合边界流、过度流(双重介质裂缝系统径向流)、基质与裂缝间窜流、整个渗流系统径向流、封闭边界流;导压系数比越大,前期压力传播越快,相同生产时间内井控面积越大;裂缝传导率比越大,整个生产期的压力下降都很显著,井控面积会迅速增大;储容比影响过渡流及窜流阶段非稳态压力传播,储容比越小,窜流越剧烈;窜流系数对窜流阶段井底压力传播有影响,窜流系数越小,窜流发生的越晚;改造半径越小,单井泄流越小,越早出现封闭边界流特征。研究成果为致密油藏直井体积压裂后裂缝及储层属性参数解释提供了理论依据。
致密油藏;体积压裂;非稳态压力分析;两区复合;拉普拉斯变换
0 引言
连续性油气聚集理论的提出以及油气工艺技术的长足发展使得致密储层的有效开发成为可能。储层压裂后最小主应力方向会发生一定角度偏转,基于这一事实,对致密油藏直井实施多次压裂可以有效拓展改造泄流区域,保证单井高产。这方面的相关研究有很多,刘雄等[1-6]运用渗透率分形理论等效描述径向裂缝的改造程度及展布情况,构建了体积压裂直井评价模型;Changan M等[7-13]基于数值模拟方法,用高渗条带替代裂缝,近似替代体积压裂区域进行模拟;Yu-long Zhao等[14-15]基于点源函数,使用双重介质描述和刻画了体积压裂区域内流体在介质中的渗流规律。此次研究基于拉式空间变换及数值反演方法,建立了致密油藏直井体积压裂非稳态压力分析半解析模型,模型考虑了生产井井筒附近多条主裂缝同时生产的情况,可以通过拟合实际井底压降试井数据给出多重压裂酸化改造后裂缝及油藏基础属性参数解释。
1 模型建立
1.1 物理模型
致密储层压裂后地层最小主应力方向会发生一定角度偏转,因此,在原有裂缝基础上再次实施压裂或者酸化改造能极大拓展裂缝分布区域,彻底改变该区域内流体的流动方式。基于实际生产井压裂情况,模型使用多条均匀分布的等效裂缝来模拟井筒附近的压裂情况,外区脆性基岩受到力的作用被拉伸或挤压,从而生成很多剪切裂缝,这里使用Warren-Root模型来描述改造区域内裂缝网络与基质之间的渗流关系以及裂缝的空间延伸情况(图1)。MEDEIROS F[16]认为,没有受到体积压裂改造影响的外围区域油层渗透率极低(上覆压力下渗透率小于0.1×10-3μm2),没有形成有效的渗流通道,对生产井贡献很少,可以忽略不计。因此,体积改造区域外边界可以看作封闭边界。综上,假设条件包括:①均质、沿半径方向属性一致;②考虑岩石、流体微可压缩,流体在储层中的流动为等温层流;③内区裂缝无限导流,各属性参数相同,外区单位体积裂缝均匀分布。

图1 致密油藏体积压裂直井物理模型
1.2 数学模型

式中:pi为原始地层压力,MPa;K为储层渗透率,10-3μm2;h为地层厚度,m;q为生产井流量,m3/d; μ为流体黏度,mPa·s;B0为原始流体体积系数,m3/m3;t为生产时间,s;φ为储层孔隙度;c为储层压缩系数,1/MPa;rf为水平井裂缝参考半长,m;rw为井筒半径,m;re为外区半径,m;α为导压系数比;β为裂缝传导率比;γ为几何修正因子,m;ω为双重介质系统储容比;λ为双重介质系统窜流系数;n为内区等效裂缝条数;b为内区等效裂缝宽度,m;η为导压系数,10-3μm2·MPa/(mPa·s)。下标:1为体积压裂内区参数;2为体积压裂外区裂缝参数;2 m为体积压裂外区基质参数。
内区流体在裂缝中渗流为线性流,其控制方程经Laplace变换后有[17]:

外区warren-Root双重介质中流体渗流表现为径向流,其拉式空间控制方程可以表述为:
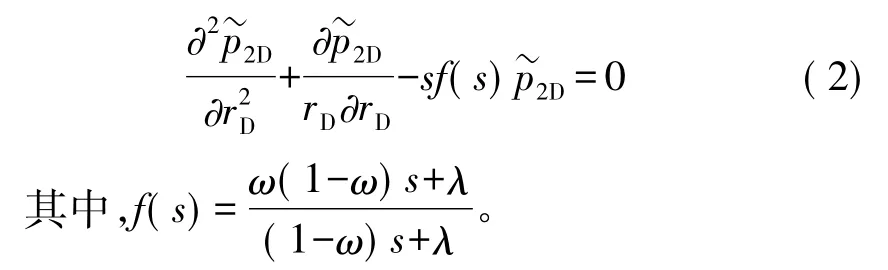
联合式(1)和式(2),结合内边界定产,外边界封闭,耦合边界处压力及流量连续等条件,可以求得内、外区拉式空间压力表达式分别为:

当rD=rwD时,带入式(3),可得拉式空间井底压力表达式:
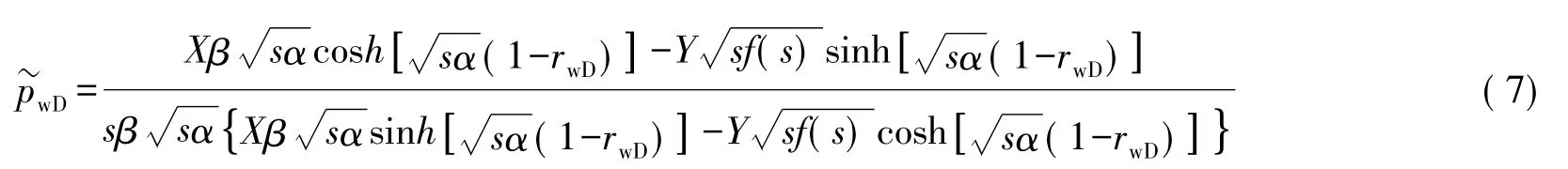
基于式(7),运用Stehfest数值反演[18]计算得到井底压力动态传播曲线图(图2)。由图2可知,整个渗流过程包括6个阶段:①人工主裂缝线性渗流阶段;②耦合边界流阶段,当储层体积压裂改造较好时,内区人工主裂缝导流能力远大于外区双重介质裂缝系统,人工主裂缝内流体迅速到达井筒,而后者不能提供足够的流体供应,压力及压力导数曲线上扬,类似弱补给或者封闭边界特征;③过渡流/双重介质裂缝系统径向流阶段;④基质与裂缝间窜流,基质渗透率极低,压力降落极其缓慢,基质与裂缝之间产生压力差,引发窜流,压力导数曲线下凹,这相比于常规双重介质,窜流发生的时间会更早,同时由于无量纲设定,窜流系数比常规双重介质大2~4个数量级;⑤整个渗流系统的径向流,压力导数曲线回归0.5水平线;⑥外封闭边界流,压力及压力导数曲线呈45°角上扬。
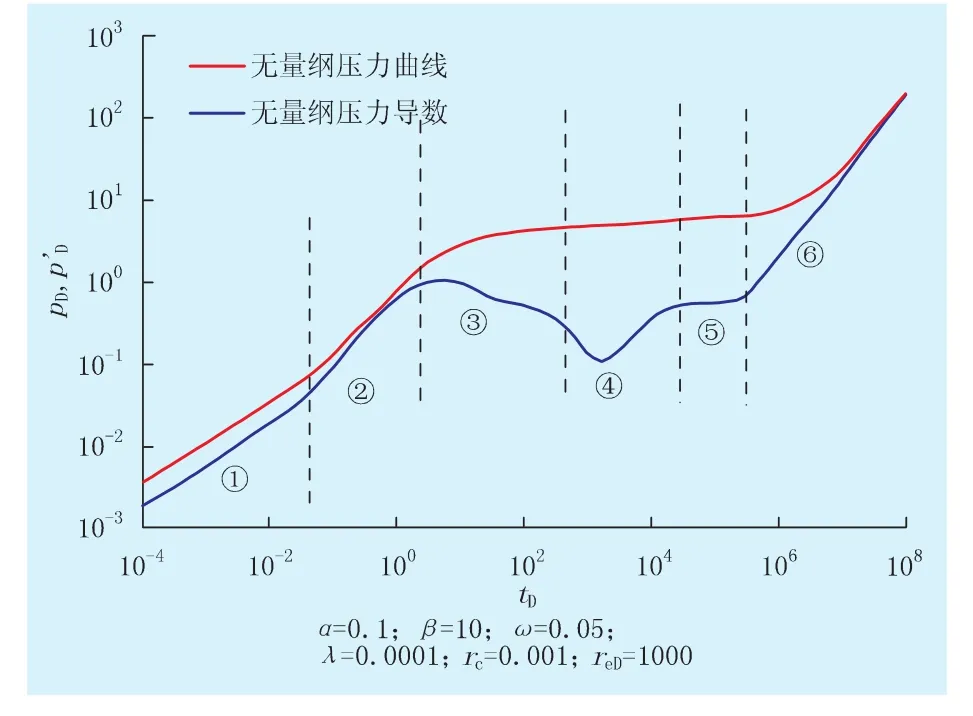
图2 井底压力响应渗流阶段划分
2 储层及裂缝参数敏感性分析
运用控制变量法,在原始模型基础上(原始模型参数见图2),变化单一参数,分析了各个储层及裂缝参数对压力动态传播的影响。
2.1 导压系数比
导压系数比α对压力传播的影响其实是体积改造区内多个裂缝参数综合影响的结果(图3),这些参数包括裂缝渗透率、裂缝储存流体的能力以及裂缝和流体对压力的敏感程度,其中内区裂缝渗透率影响最为显著。由图3可知,导压系数比对初期压力传播有影响,导压系数比越大,生产井前期压力传播越快,相同生产时间内井控面积越大,导压系数比对初期井底压力变化的影响随着其数值的增大而减弱,说明增加人工裂缝改造程度对单井控制面积的影响是存在优化范围的。另外,导压系数比变化对复合边界流影响微弱。

图3 导压系数比对压力传播的影响
2.2 裂缝传导率比
裂缝传导率比β体现了内外区改造体积比值对压力传播的影响,主要体现在内区裂缝条数的增加上(图4)。由图4可知,裂缝传导率比越大,整个生产期的压力下降都很显著,井控面积会迅速增大。说明增大近井区域压裂改造缝网,能大幅度提高泄流面积,且这样的改造措施对整个生产期都有显著效果。

图4 裂缝传导率比对压力传播的影响
2.3 储容比

图5 储容比对压力传播的影响
研究不同储容比ω对井底压力动态传播的影响(图5)。由图5可知,储容比主要影响外部双重介质系统窜流发生的程度,储容比影响过渡流及窜流阶段的非稳态压力传播,储容比越小,窜流越剧烈,在无量纲压力导数曲线上表现为下凹趋势越深,过渡流阶段井底压力变化更为剧烈。
2.4 窜流系数
研究不同窜流系数λ对井底压力动态传播的影响(图6)。由图6可知,窜流系数影响外部区域双重介质系统窜流发生的时间,窜流系数对窜流阶段井底压力传播有影响,窜流系数越小,基质向裂缝流动引发窜流就越晚。

图6 窜流系数对压力传播的影响
2.5 改造半径
研究改造半径reD对井底压力动态传播的影响情况(图7)。由图7可知:改造半径越小,单井泄流越小,越快出现封闭边界流特征,增加裂缝延伸长度能够延缓封闭边界流发生的时间,以确保较长稳产期。
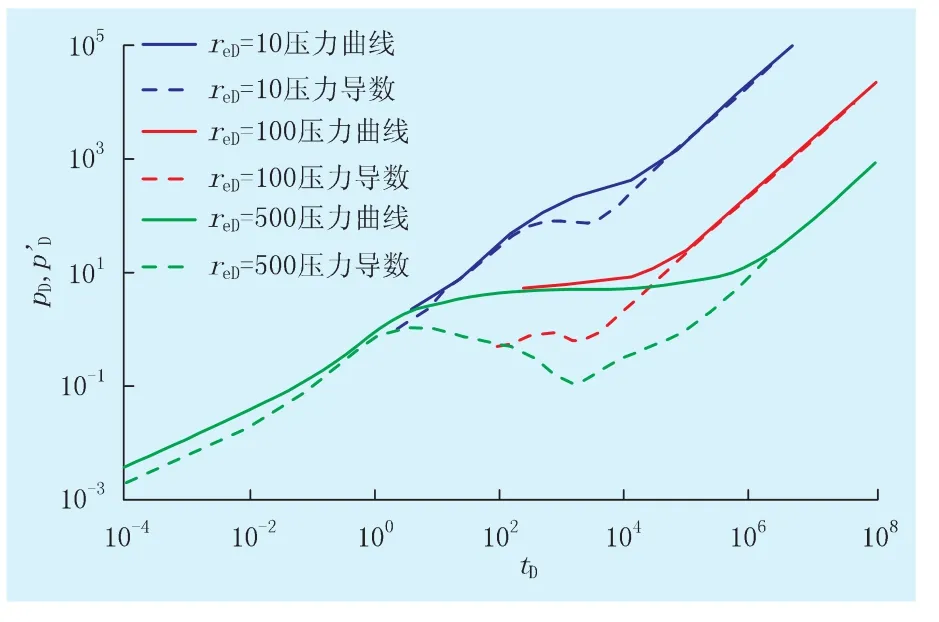
图7 改造半径对压力传播的影响
3 应用实例
目标区块为新疆某三叠系砂砾岩油藏,近源堆积,非均质性强,厚度大,储层致密,低孔低渗。实例井共经历了2次水力压裂和1次酸化压裂改造,由于压裂后地层最小主应力方向会发生改变,因此,井筒附近形成了多条主裂缝。利用已建立的数学模型对该井试井数据进行拟合(图8),结合无量纲化定义式,得到了多重压裂改造后该井裂缝及储层参数解释:内区渗透率为1.160×10-3μm2,外区渗透率为0.690×10-3μm2,基质渗透率为0.053× 10-3μm2,内区裂缝等效宽度为0.022 m,外边界改造半径为400 m。从解释数据可以看出,体积压裂对储层有明显的改造作用。内区裂缝改造不足,初期压力传播缓慢,井控范围小,单井产量偏低。但体积改造外边界半径大,较晚进入拟稳态阶段,保证了较长的生产期,在没有进一步压裂改造前提下,加密井在不考虑自身控制范围情况下,至少保证井距在400 m以上才能防止井间干扰。另外,基于上述模型参数,对该井改造后产能进行了预测,将实测产量数据与预测曲线进行对比(图9)。由图9可知,预测结果较为吻合,验证了模型的实用性。
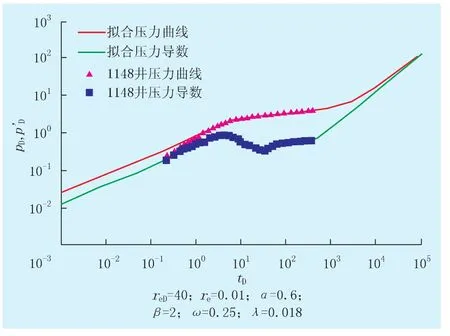
图8 井底压力响应曲线拟合
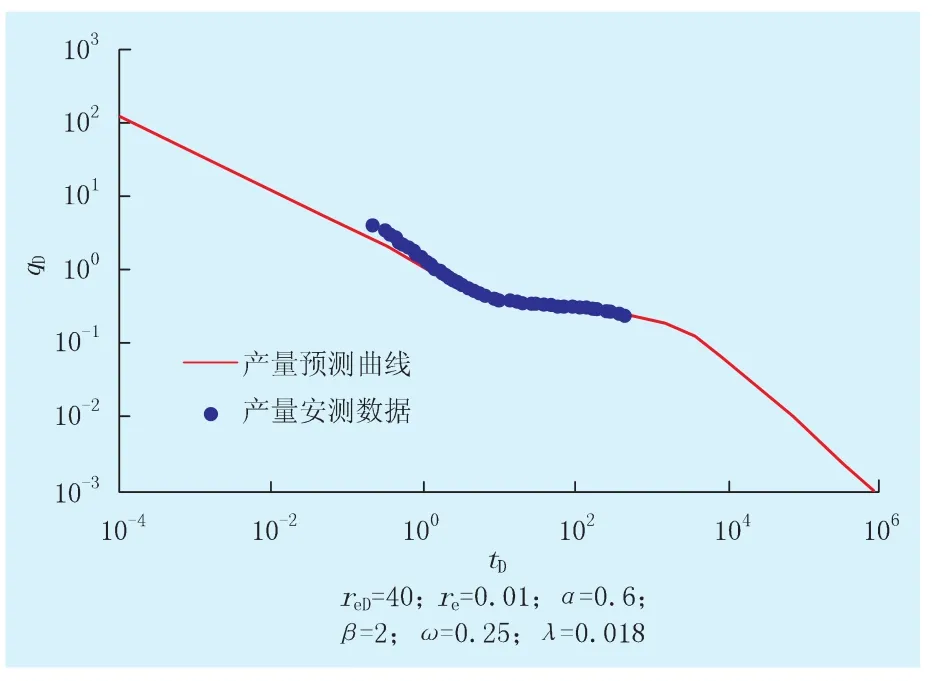
图9 产量预测与实测数据对比
4 结论
(1)建立了致密油藏直井体积压裂非稳态压力分析模型,渗流过程包括6个阶段即:线性流、耦合边界流、过度流、基质-裂缝窜流、径向流、封闭边界流。
(2)导压系数比对初期压力传播有影响,导压系数比越大,井底初期压力传播越快,相同生产时间内井控面积越大;裂缝传导率比越大,整个生产期的压力下降都很显著,井控面积会迅速增大,增大近井区域压裂缝改造范围,能大幅度提高单井泄流面积。
(3)储容比影响外部双重介质系统窜流发生的程度,影响过渡流及窜流阶段的非稳态压力传播,储容比越小,窜流越剧烈;窜流系数对窜流阶段井底压力传播有影响,窜流系数越小,基质向裂缝流动引发窜流就越晚。
(4)改造半径越小,单井泄流越小,越快出现封闭边界流特征,增加裂缝延伸长度能够延缓封闭边界流发生的时间,以确保较长稳产期。
[1]刘雄.致密油储层体积改造产能评价方法研究[D].中国地质大学(北京),2013:27-58.
[2]刘雄,田昌炳,姜龙燕,等.致密油藏直井体积压裂稳态产能评价模型[J].东北石油大学学报,2014,38 (1):91-96.
[3]刘雄,田昌炳,万英杰,等.裂缝性致密油藏直井体积改造产能评价模型[J].现代地质,2015,29(1):131-137.
[4]Lei Xiao,Gang Zhao.A novel approach for determining wormhole coverage in chops wells[C].SPE157935,2012.
[5]Liu X,Zhao G.A fractal wormhole model for cold Heavy oil production[J].Journal of Canadian Petroleum Technology,2005,44(9):31-36.
[6]王文东,赵广渊,苏玉亮,等.致密油藏体积压裂技术应用[J].新疆石油地质,2013,34(3):345-348.
[7]Chang M,Xu Zhang,Lang Zhan,et al.Modeling hydraulic fracturing induced fracture networks in shale gas reservoirs as a dual porosity system[C].SPE132180,2010.
[8]王文东,苏玉亮,慕立俊,等.致密油藏直井体积压裂储层改造体积的影响因素[J].中国石油大学学报:自然科学版,2013,37(3):93-97.
[9]陆程,刘雄,程敏华,等.页岩气体积压裂水平井产能影响因素研究[J].特种油气藏,2014,21(4):108-112.
[10]Arvind Harikesavanallur,Franz Deimbacher,Martin Crick,et al.Volumetric fracture modeling approach (VFMA):Incorporating microseismic data in the simulation of shale gas reservoirs[C].SPE134683,2010.
[11]Khalid M,Mansour A.Tight oil reservoir development feasibility study using finite difference simulation and streamlines[C].SPE126099,2009.
[12]Cipolla C L,Carbo Ceramics,Lolon E P,et al.Reservoir modeling and production evaluation in shale-gas reservoirs[C].IPTC13185,2009.
[13]Barry Rubin.Accurate simulation of non-darcy flow in stimulated fractured shale reservoirs[C].SPE132093,2010.
[14]Yu-long Zhao,Lie-hui Zhang,Feng Wu.Pressure transient analysis for multi-fractured horizontal well in shale gas reservoirs[J].Journal of Prtroleum Science and Engineering,2012,90/91(6):31-38.
[15]王晓冬,罗万静,侯晓春,等.矩形油藏多段压裂水平井不稳态压力分析[J].石油勘探与开发,2014,41 (1):74-78.
[16]Medeiros F,Kurtoglu B,Ozkan E,et al.Pressuretrasient performance of hydraulically horizontal well in locally and globally naturally fractured formations[C].Dubai:International Petroleum Technology Conference,2007:1-10.
[17]葛家理,宁正福,刘月田,等.现代油藏渗流力学原理[M].石油工业出版社,2003:189-194.
[18]Stehfest H.Numerical invesion of Laplace transforms[J].Communications of the ACM,1970,13(1):47-49.
编辑张耀星
TE348
A
1006-6535(2015)05-0095-05
20150519;改回日期:20150715
国家科技重大专项“低渗、特低渗油田数模方法与油藏工程研究”(2011ZX05013-004)
刘雄(1988-),男,2010年毕业于中国地质大学(北京)石油工程专业,现为中国石油勘探开发研究院油气田开发工程专业在读博士研究生,从事油气田开发方面的研究。
10.3969/j.issn.1006-6535.2015.05.020

