Taguchi optimization of process parameters in friction stir processing of pure Mg

*

School of Metallurgy and Materials,College of Engineering,University of,Tehran,PO Box 1155-4563,Tehran,Iran

Taguchi optimization of process parameters in friction stir processing of pure Mg

D.Ahmadkhaniha*,M.Heydarzadeh Sohi,A.Zarei-Hanzaki,S.M.Bayazid,M.Saba

School of Metallurgy and Materials,College of Engineering,University of,Tehran,PO Box 1155-4563,Tehran,Iran

Taguchi experimental design technique was applied to determine the most infuential controlling parameters of FSP such as tool rotational speed,travel speed,tilt angle and penetration depth on hardness value of Mg.In this case,9 combinations of these 4 essential processing parameters were set and Taguchi's method followed exactly.Signal to noise ratio(S/N)analysis showed that maximum hardness achieved when rotational and travel speeds,penetration depth and tilt angel were chosen as 1600 rpm,63 mm/min,0.1 mm and 2°,respectively.In addition, analysis of variance(ANOVA)technique indicated that tilt angle and rotational as well as travel speed are the signifcant infuential parameters in the hardness value of the treated samples,respectively.Finally a model for hardness values based on FSP parameters was calculated by design expert which was also confrmed by experimental results.

Mg;FSP;Hardness;Taguchi;ANOVA;Design-expert

1.Introduction

Magnesium and its alloys have received considerable attention as biodegradable implants during recent years. However,their biomedical applications are still limited due to their poor mechanical and corrosion resistance[1,2].High degradation rate of Mg based materials deteriorates their mechanical integrity during the healing process.Many techniques have been applied to improve corrosion resistance of magnesium alloys,such as alloy modifcation[3],producing composites[4,5]and surface treatment[6-8]. Among this variety of methods,the one which can improve both corrosion and mechanical properties of magnesium would be more promising.Previous studies have shown that the grain refnement can enhance mechanical properties [9,10]and corrosion resistance simultaneously[11-13]. Different severe plastic deformations have been used to modify the structure of materials[14-17].Friction stir processing(FSP),which can signifcantly refne structure [18,19]and fabricate composites[20,21]can be considered as a severe plastic deformation to modify the structure of materials.FSP requires a precise design of process parameters in order to achieve a defect free workpiece that is consistently reproducible.Since magnesium holds hexagonal close packed structure,the successful achievement of fne grains in Mg by FSP might be very sophisticated due to its limited slip systems.In addition,there are several FSP parameters that affect the structure and mechanical properties of Mg;therefore,a large number of experiments should be done to achieve a fne grained Mg structure with enhanced mechanical properties.

Jayaraman et al.[22]determined optimum welding condition for maximizing tensile stress of cast aluminum alloys byANOVA and signal to noise ratio.S.Rajakumar et al.[23] focused on the development of empirical relationship to predict tensile strength of friction stir welded AA 1100 aluminum alloy joints.The results showed that rotational speed is more sensitive than tool hardness,followed by axial force,shoulder diameter,pin diameter and welding speed on tensile strength. Lakshminarayanan et al.[24]indicated that the rotational speed,welding speed and axial force are the most infuential parameters on the tensile strength of aluminum alloy joints. Nourani et al.[25]confrmed that Taguchi's orthogonal design can be successfully used to minimize both the HAZ distance to the weld line and the peak temperature in aluminum alloys.M. Salehi et al.[26]applied design of experiment(DOE)to determine the most important factors of friction stir processing which infuence ultimate tensile strength(UTS)of AA6061/ SiC nanocomposites.Analysis of variance revealed that the rotational speed has signifcant impact.The statistical results depicted that higher UTS achieves by threaded pin,higher rotational and lower the transverse speed.

This work has been conducted to fnd optimal FSP parameters,such as rotational(W)and travel(V)speeds,tool penetration depth(PD)and tilt angle(Θ)in order to fabricate fne grained magnesium workpiece.Analysis of variance (ANOVA)along with the Taguchi technique and design-expert software was used to interpret experimental data.

2.Experimental design and procedure

The Design-Expert,statistical software along with Taguchi design with L9 orthogonal array which composed of 3 columns and 4 rows were employed to optimize the FSP parameters(Table 1).The selected FSP parameters for this study were:rotational speed(W),travel speed(V),tilt angle(Θ)and penetration depth(PD).The Taguchi method was applied to the experimental data and thesignal to noise ratio(S/N)for each level of process parameters is measured based on the S/N analysis.Regardless of the category of the quality characteristic,a higher S/N ratio corresponds to a better quality characteristic.Therefore,theoptimalleveloftheprocess parameters is the level with the highest S/N ratio[27].A detailed ANOVA framework for assessing the signifcance of the process parameters is also provided.The optimal combination of the process parameters can be then predicted. Finally,a model for hardness values based on FSP parameters is offered by design expert.

As cast Mg workpieces(100×50×7 mm)were prepared and FSP were applied on the surface of the workpieces using a conventional miller machine.A triangle FSP tool withshoulder diameter of 20 mm was machined from H13 tool steel.A Vickers microhardness tester(HV-5,Laizhou Huayin Testing Instrument Co.Ltd)with an applied load of 200 gf for 10 s was used to measure the hardness of the workpieces.In this study,the hardness value of stir zone which experiences the highest strain and heat input by FSP,is determined for optimizing the FSP parameters.

Table 1FSP parameters and design levels.

3.Results and discussion

3.1.Signal to noise ratio(S/N)analysis

Signal to noise ratios(S/N)for each control factor were calculated,in order to minimize the variances in hardness values.The signals indicate that the effect on the average responses and noises are calculated by the infuence on the deviations from the average responses,which will disclose the sensitiveness of the experiment output to the noise factors.The appropriate S/N ratio must be chosen according to previous knowledge,expertize and understanding of the process.When the target is determined and there is static design,it is possible to choose the S/N ratio based on the goal of the design.In this study,the S/N ratio was chosen based on the criterion thehigher-the-better,to minimize the responses and it was calculated according to Eq.(1)[27];

where n is repetitions that in this study is equal to 3 and Yiis the hardness result for the ith experiment.

The Taguchi experimental results are summarized in Table 2 and presented in Fig.1.

As is seen in Fig.1,the highest hardness was achieved when W,V,Θ and PD were chosen according to level 3,3,2, and 1,respectively.

FSP encourages recrystallization phenomena due to high strain and heat input and refnes the structure.Higher strain and lower heat input result in fner microstructure and enhance hardness value.Induced strain rate and heat input during FSP can be calculated by Eq.(2)[18]and Eq.(3)[28].Too high value of rotational to travel speed ratio(W/V)for a relativelysoft material such as pure Mg tends to generate high amounts of heat according to Arbegast and Hartley equation(Eq.(2)) [18].

Table 2Standard orthogonal arrays of 9 different groups following Taguchi's suggestion.

Fig.1.The effect of parameters(a)W,(b)V,(c)PD,(d)Θ on hardness and S/N ratio of the responses.

where the exponent α and the constant K are in the range of 0.04-0.06 and 0.65 to 0.75,respectively,Tm(°C)is the melting point,T is the achieved temperature,W and V are rotational and travel speed,respectively.Meanwhile,with increasing W,strain rate(3°)is increased according to Eq.(3), [28].

where re and Le are the average radius and depth of the dynamically recrystallized zone.Rm is about half of the rotational speed(W).Increasing PD,induces higher force to the materials.Θ determines the interface of shoulder and material.Higher Θ results in less interface and results in less friction of two surfaces.On the other hand,higher PD increases the interface of material with FSP tool and enhances stress as well as heat input.Therefore,a good combination of FSP parameters can result in fner structure and higher hardness.

3.2.ANOVA analysis of variance

Analysis of variance(ANOVA)test was performed to identify the most effective process parameters which affect the hardness of FSPed materials.The ANOVA results and dynamic response table for S/N ratio are listed in Tables 3 and 4, respectively.Precision of a parameter estimation is based on the number of independent samples of information which can be determined by degree of freedom(DOF).The degree of freedom is equal to the number of experiments minus the number of additional parameters estimated for that calculation.

The results of ANOVA indicate that Θ,V,Wand PD are the process parameters that have signifcant contribution on the hardness values of FSPed materials,respectively.

In addition,a numerical model by design expert has been developed and the analysis of variance(ANOVA)by design expert is presented in Table 5.The R2coeffcient indicates thegoodness of ft for the model.In this case,the value of the coeffcient(R2=0.9997)indicates that 99.97%of the total variability is explained by the model after considering the signifcant factors.The F-value of 434.96 implies the model is signifcant.There is only a 3.69%chance that a“Model FValue”this large could occur due to noise.Values of“Prob＞F”less than 0.05 indicate model terms are signifcant. In this case C(tilt angle),AB(rotational×travel speeds)are signifcant model terms.Values greater than 0.1 indicate the model terms are not signifcant.

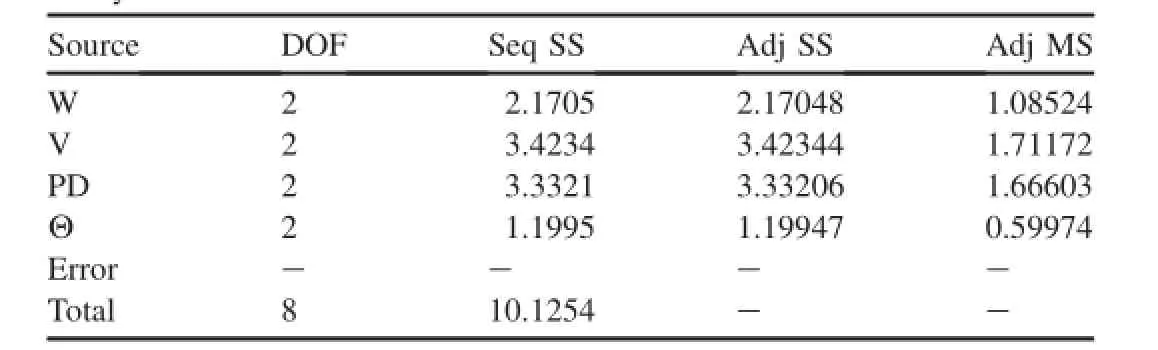
Table 3Analysis of Variance for SN ratios.

Table 4Response table for signal to noise ratios(dynamic response).

Table 5ANOVA for response surface reduced 2FI model.

The“Pred R-Squared”of 0.9544 is in reasonable agreement with the“Adj R-Squared”of 0.9974.The“adequate precision”measures the signal to noise ratio.A ratio greater than 4 is desirable.The ratio of 66.554 indicates an adequate signal. This model can be used to navigate the design space.

The fnal mathematical model in terms of actual factors as determined by design expert software is written in Eq.(4).

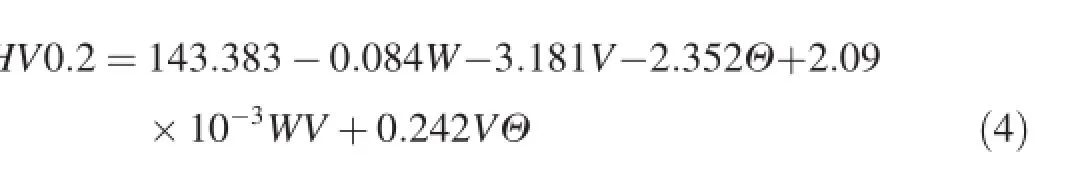
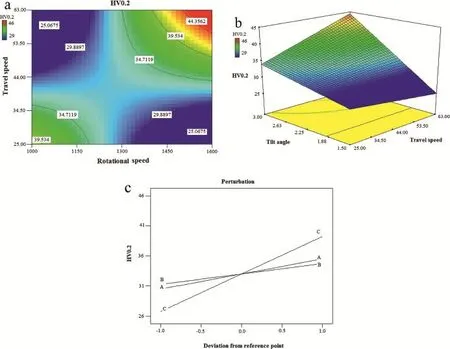
Fig.2.Effects of FSP parameters on hardness value(a)infuence of W and V,(b)infuence of Θ and V,(c)perturbation plots.

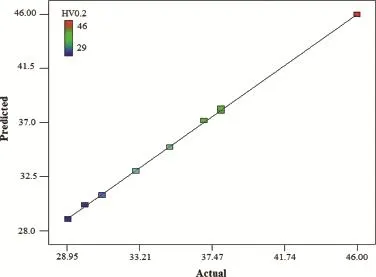
Fig.3.The graph of the predicted versus the experimental data.

The effect of processing parameters on the hardness values is shown in Fig.2.The hardness value is found to rise as rotational and travel speeds are increased(Fig.2a);while in mediate limits of rotational and travel speeds,the hardness values are decreased.The surface plot(Fig.2b)discloses the interaction between the tilt angle and the travel speed effect on hardness values.Hardness value is found to increase as tilt angle is increased at high travel speed.In addition,it is shown in Fig.2b that effect of tilt angle variation on hardness value is much more signifcant at high travel speed than low travel speed.Fig.2c demonstrates perturbation plots which illustrate the effect of the FSP parameters on hardness value for an optimization design,this graph shows how the response changes as each factor moves from a chosen reference point, with all other factors held constant at the reference value[29]. A steep slope or curvature of a factor indicates that the response is sensitive to that factor.Hence,the plot shows that tilt angle is mostly affected the hardness value followed by rotational and travel speeds.

To validate the model,a set of experiments were performed. The graph of the predicted versus the experimental data is shown in Fig.3.The graph shows that there is a good agreement between the model and the experimental data.Therefore, the model can be used to predict hardness values of friction stir processed pure Mg.

4.Conclusion

The present study was aimed to identify the optimal and most infuencing FSP parameters on hardness of pure Mg by conducting minimum number of experiments using Taguchi orthogonal array.Various combinations of processing parameters were considered to evaluate the relative importance of parameters.FSP parameters including W = 1600 rpm, V=63 mm/min,PD=0.1,Θ=2°have been found to be the optimal parameters.In addition,a numerical model has been developed by design expert and it was shown that tilt angle and rotational speed as well as travel speed have the most signifcant effect on hardness value of FSPed Mg.

[1]F.Witte,Acta Biomater.6(2010)1680-1692.

[2]M.P.Staigera,A.M.Pietaka,J.Huadmaia,G.Dias,Biomaterials 27 (2006)1728-1734.

[3]E.Zhang,L.Yang,J.Xua,H.Chen,Acta Biomater.6(2010) 1756-1762.

[4]A.Feng,Y.Han,Mater.Des.32(2011)2813-2820.

[5]K.Abdelrazek Khalil,A.A.Almajid,Mater.Des.36(2012)58-68.

[6]H.Hornberger,S.Virtanen,A.R.Boccaccini,Acta Biomater.8(2012) 2442-2455.

[7]L.Li,J.Gao,Y.Wang,Surf.Coat.Technol.185(2004)92-98.

[8]Y.Wang,M.Wei,J.Gao,Mater.Sci.Eng.C 29(2009)1311-1316.

[9]Y.J.Kwon,I.Shigematsu,N.Saito,Mater.Trans.45(2004)2304-2311.

[10]W.M.Gana,M.Y.Zhenga,H.Changa,X.J.Wanga,X.G.Qiaoa,K.Wua, B.Schwebkeb,H.G.Brokmeierb,J.Alloys Compd.470(2009) 256-262.

[11]H.Wang,Y.Estrin,H.Fu,G.Song,Z.Zu´berov′a,Adv.Eng.Mater.9 (2007)967-972.

[12]Y.Chino,T.Hoshika,M.Mabuchi,Mater.Trans.47(2006)1040-1046.

[13]G.Ben Hamua,D.Eliezer,L.Wagner,J.Alloys Compd.46(2009) 222-229.

[14]J.H.Gao,S.K.Guan,Z.W.Ren,Y.F.Sun,S.J.Zhu,Mater.Lett.65(2011) 691-693.

[15]H.Seop Hana,Y.Minghuia,H.Kwang Seoka,J.Young Byunb,P.Ryung Chac,S.Jo Yangd,Y.Chan Kima,J.Mech.Behav.Biomed.Mater.20 (2013)54-60.

[16]Q.Penga,X.Lia,N.Maa,R.Liua,H.Zhang,J.Mech.Behav.Biomed. Mater.10(2012)128-137.

[17]C.op't Hoog,N.Birbilis,Y.Estrin,Adv.Eng.Mater.10(2008)579-582.

[18]R.S.Mishra,Z.Y.Ma,Mater.Sci.Eng.R 50(2005)1-78.

[19]P.Asadi,M.K.Besharati Givi,N.Parvin,A.Araei,M.Taherishargh, S.Tutunchilar,Int.J.Adv.Manuf.Technol.63(2012)9-12.

[20]A.Shahi,M.Heydarzadeh Sohi,D.Ahmadkhaniha,M.Ghambari,Int.J. Adv.Manuf.Technol.75(2014)1331-1337.

[21]P.Asadi,G.Faraji,M.Besharati,Int.J.Adv.Manuf.Technol.51(2010) 247-260.

[22]M. Jayaraman, R. Sivasubramanian, V. Balasubramanian, A.K.Lakshminarayanan,J.Sci.Ind.Res.68(2009)36-43.

[23]S.Rajakumar,C.Muralidharan,V.Balasubramanian,Int.J.Microstruct. Mater.Prop.6(2011)132-156.

[24]A.K.Lakshminarayanan,V.Balasubramanian,Trans.Nonferrous Met. Soc.China 18(2008)548-554.

[25]M.Nourani,A.S.Milani,S.Yannacopoulos,Engineering 3(2011) 144-155.

[26]M.Salehi,M.Saadatmand,J.Aghazadeh Mohansedi,Trans.Nonferrous Met.Soc.China 22(2012)1055-1063.

[27]R.K.Roy,A Primer on the Taguchi Method,Van Nostrand Reinhold,NY, 1990,pp.100-154.

[28]C.I.Chang,C.J.Lee,J.C.Huang,Scr.Mater.51(2004)509-514.

[29]S.T.Manavalan,R.Muralidharan,J.Sep.Sci.30(2007)3143-3315.

Received 9 March 2015;revised 10 April 2015;accepted 16 April 2015 Available online 13 May 2015

*Corresponding author.Tel.:+98 9126174090.

E-mail address:ahmadkhany@ut.ac.ir(D.Ahmadkhaniha).

Peer review under responsibility of National Engineering Research Center for Magnesium Alloys of China,Chongqing University.

http://dx.doi.org/10.1016/j.jma.2015.04.002.

2213-9567/Copyright 2015,National Engineering Research Center for Magnesium Alloys of China,Chongqing University.Production and hosting by Elsevier B.V.All rights reserved.

Copyright 2015,National Engineering Research Center for Magnesium Alloys of China,Chongqing University.Production and hosting by Elsevier B.V.All rights reserved.