基于MOPSO的RC单柱墩全寿命抗震性能多目标优化设计

柳春光，吕晓莹，张士博

(大连理工大学 建设工程学部， 辽宁 大连 116024)

基于MOPSO的RC单柱墩全寿命抗震性能多目标优化设计

柳春光，吕晓莹，张士博

(大连理工大学 建设工程学部， 辽宁 大连 116024)

采用MATLAB模块化编程将多目标粒子群优化算法MOPSO和反应谱分析联合起来进行抗震优化设计。根据桥墩在E1和E2两级设防水准地震作用下的抗震性能，采用Pushover分析墩顶的最大漂移率以及概率统计的方法得到全寿命期费用模型对应的工程费用，从而得到费用最小的Pareto解。数值计算结果表明：MOPSO算法和反应谱分析结合能够很好的应用于桥梁全寿命抗震性能设计分析，算法的收敛性和稳定性好，所求得的Pareto最优解在解空间分布均匀且范围较广，可以为桥梁设计提供良好的方案选择空间。

单柱墩抗震；MOPSO算法；全寿命费用；抗震性能优化

桥梁工程作为生命线工程，一旦遭受地震破坏，除了结构的损坏，更重要的是对震后减灾和救援工作形成巨大的障碍。1971年美国的San Fernando地震对该地区一系列生命线工程造成的灾难性后果，推动了生命线工程的抗震发展。桥梁抗震技术也迅速发展[1-2]，逐渐由传统的保证结构强度向基于性能的全寿命设计转变[3]。基于“投资-效益”准则的性能设计和全寿命设计自20世纪90年代以来历经十几年的发展，取得了卓有成效的成果。Liu等[4]首先提出了以结构初始造价加上全寿命期间地震造成的损失作为总造价为目标来优化结构抗震设计的方法。王光远等[5]提出了结构抗震全寿命预期总费用的最优设计方法。马军海等[6]提出了一个桥梁全寿命设计的整体框架。邵旭东等[7]提出以桥梁全寿命成本最小为优化目标来进行桥梁性能的设计方法，通过对衡炎高速公路窑背大桥[8]进行分析，验证了全寿命设计方法的合理性和有效性。谢楠等[9]利用改进的遗传算法对桥梁抗震进行优化设计并快速得到优化解。进化多目标遗传算法的发展[10]，也促进了桥梁全寿命抗震的优化设计。郑玉国等[11]建立了一种将多目标遗传优化算法和桥梁抗震设计中常用的反应谱法相结合起来用于规则钢筋混凝土(Reinforced Concrete，RC)圆截面单柱墩优化设计的方法，将桥墩抗震优化设计转为多目标优化问题。同时柳春光等[12]也运用多目标非劣排序精英遗传优化算法(NSGA-Ⅱ)对规则圆形独柱桥墩全寿命性能优化分析并得到较好的性能解。然而Coello等[13]提出的多目标粒子群算法(MOPSO)具有很快的收敛速率，并且引入自适应网格的机制来保存Pareto最优解和新的变异机制来提高性能解的分布范围。因此，本文采用MOPSO算法来进行规则RC桥梁圆形截面独柱墩的全寿命多目标抗震优化设计，以验证该算法在桥梁工程中的适用性。

1 优化模型及算法

1.1 全寿命抗震多目标性能优化模型

鉴于柳春光等[12]提出的基于桥梁全寿命抗震性能的多目标优化模型考虑因素较全面，易于程序化，故本文依然采用该模型。该模型能够考虑结构初始造价，地震损伤期望，正常运行期间的检查维护费用，后期结构拆除费用和残余价值以及环境污染费用。目标函数是使C0(X)，E(X)和Ce(X)同时取得最小值，具体公式如下：

(1)

此外，本论文只考虑水平地震力下的作用，根据Wen等[14]的研究可认为单个随机荷载可用泊松分布来描述，此时结构的损失期望可简化以下公式：

(2)

其中：Ck为第k个破坏水平下的损失值；Pk为第k个破坏水平下的失效概率；υ为地震年发生概率。其中损失值及失效概率的计算是以Pushover计算出的墩顶位移漂移率(即墩顶位移与墩高的比值)为指标，详见文献[9]。

1.2 MOPSO多目标粒子群算法及优化过程

MOPSO多目标粒子群算法[13]与其他粒子群算法相比有以下两方面较大的改进：(1) 引入一个能够自适应扩展的外部存档来存储非劣解，即Pareto最优解；(2) 引入特殊的变异算子实现粒子群及决策变量的范围在求解过程中都不断变化,使得粒子群搜索空间能够最大化，提高最优解的分布。利用MATLAB对MOPSO进行模块化编程，以桥墩的纵筋配筋率ρ1、箍筋配筋率ρ2和直径D为设计变量。

采用MOPSO的规则RC桥梁圆截面单柱墩的全寿命抗震性能优化设计的求解过程见图1。

图1 基于MOPSO全寿命抗震性能的优化设计流程图

其中需要说明的是：(1) 编制MATLAB程序在循环迭代时自动调用外部程序OpenSees，按照《公路桥梁抗震细则》[15](JTG/TB02-01—2008)的要求对给定参数下桥墩抗震性能设计过程分别进行重现期较短的地震(E1水平地震作用，对应第一级设防水准)的验算和重现期较长的地震作用(E2水平地震作用，对应第二级设防水准)作用下的Pushover验算；(2) 对一次迭代时不能通过抗震性能验算的设计方案，其初始造价会增加一个非常大的正值(程序中取为1×1010)，使对应的粒子在该次迭代过程后不能选作为非支配解，从而保证算法循环迭代过程中粒子群数保持不变，同时也能够直观的判断算法求解得到的Pareto最优解的准确性；(3) 粒子更新速度、位置时会受到其自身的最优位置(即局部最优解Pbest)和全局粒子的最优解(即全局最优解Gbest)的双重影响；(4) 当粒子某个变量的值超越了边界值，算法会采取将粒子的速度乘以负1，使其超反方向继续搜索，再重新更新自身的位置；(5) 每次循环结束后都会在种群中选出非支配解，按照Pareto占优机制将其与外部存档中的非支配解进行二次对比筛选，从而获得新的最优解集；(6) 当外部存档中的非支配解的数量达到其最大存储能力，算法会自动启动自适应网格法则，动态调整粒子的位置。

2 实例计算

2.1 算例

为了验证MOPSO算法在规则RC桥梁圆截面单柱墩全寿命抗震性能优化设计中的适用性及合理性，对文献[12]中的算例进行数值分析，该算例的具体资料如下：

某高架桥：设计使用寿命100 a，中等规则，C类等级，抗震设防烈度7°，水平向设计地震加速度峰值0.15g，所处场地类型为Ⅱ类，场地特征周期为0.40 s，水平地震反应谱的场地系数Cs=1.0，E1地震作用下抗震重要性系数Ci=0.34，E2地震作用下Ci=1.0。此外，混凝土单价为295元/m3，纵筋单价为27 690元/m3，箍筋单价为26 676元/m3。

决策变量的约束条件如下：

(3)

2.2 结果分析

MOPSO算法的相应各参数如下：种群大小为100，外部存档最优解数为250，循环迭代次数为50，惯性权重w为0.73，外部存档网格剖分数为10。各参数的选取参照Coello等[13]建议的算法参数取值范围。

图2和图3分别给出了初始种群和循环迭代结束后外部存档中的非支配解(即Pareto最优解)在解空间的分布情况，由图可知采用MOPSO优化后的解分布均匀和覆盖范围广，表明算法收敛性较好，也验证了本文提出的抗震性能优化方法的有效性。其中图3中给出的全寿命费用最小的设计方案能为业主提供更广泛的选择空间。图4给出了最优解和初始解对应的全寿命中三种工程费用，其中初始解中有两个解不能满足抗震规范的要求，根据算法的设置其初始造价数值达到1 010元，因数值太大在图中未画出，同时也验证了本文提出的方法能有效提高方案比选的效率。图5给出了MOPSO算法三次分别计算的最优解，并与文献[12]中的计算结果进行了比较，由图可以看出三次计算结果与文献中的结果基本一致，表明该算法的稳定性较好。

图2 初始解空间的分布

图3 MOPSO优化及全寿命最优结果

图4 最优解与初始解费用的对比

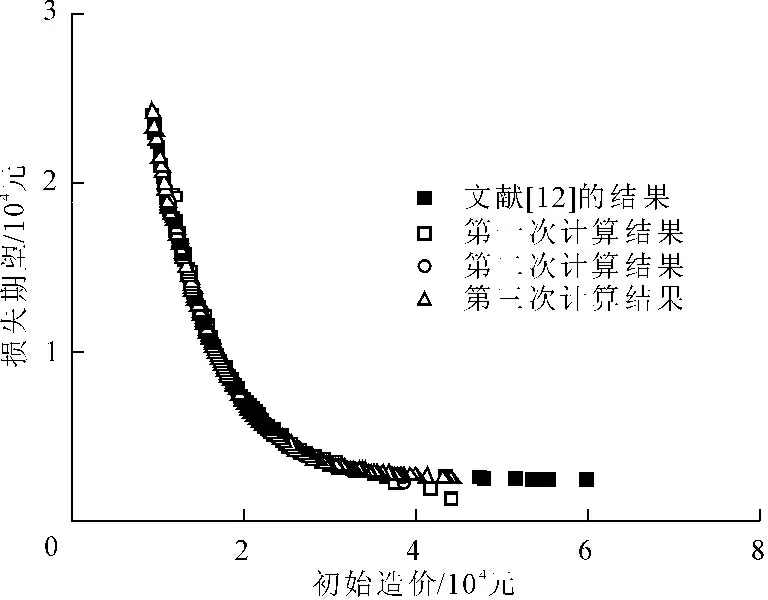
图5 计算结果对比

3 结 论

本文联合多目标粒子群优化算法(MOPSO)和反应谱分析，采用MATLAB编程，成功运用于规则RC桥梁圆截面单柱墩全寿命抗震性能优化设计，得出以下结论：

(1) 利用MATLAB编程能将MOPSO算法和Pushover分析很好的应用于桥梁全寿命抗震优化设计，并且算法的稳定性和收敛性较好；

(2) 数值计算结果表明：所求得的Pareto最优解在解空间分布均匀，范围较大，表明算法搜索能力能较好的覆盖所有决策变量的范围，保证解的准确性和可靠性；

(3) 该方法能够高效的计算出一定范围内并且满足抗震性能要求的单柱墩全寿命优化方案，为设计者或业主提供良好的方案选择空间。

[1] 杜修力，韩 强.桥梁抗震研究若干进展[J].地震工程与工程振动，2014(4):1-14.

[2] 杨仲会.高墩铁路大跨度连续梁桥抗震支座的设计与施工[J].水利与建筑工程学报，2009，7(4):103-104，133.

[3] 马 建，孙守增，杨 琦，等.中国桥梁工程学术研究综述[J].中国公路学报，2014，27(5):1-96.

[4] Liu, S C, F Neghabat. A cost optimization model for seismic design of structures[J]. Bell System Technical Journal, 1972，51(10):2209-2225.

[5] 王光远，季天健,张 鹏.抗震结构全寿命预期总费用最小优化设计[J].土木工程学报，2003，36(6):1-6.

[6] 马军海,陈艾荣,贺 君.桥梁全寿命设计总体框架研究[J].同济大学学报：自然科学版,2007，35(8):1003-1007.

[7] 邵旭东，彭建新，晏班夫.桥梁全寿命设计方法框架性研究[J].公路，2006(1):44-49.

[8] 彭建新，邵旭东，张建仁.桥梁全寿命设计理论、方法和实践[C]//第十九届全国桥梁学术会议.中国上海，2010.

[9] 谢 楠，陈英俊.遗传算法的改进策略及其在桥梁抗震优化设计中的应用效果[J].工程力学，2000，17(3):31-36.

[10] 公茂果，焦李成，杨咚咚，等.进化多目标优化算法研究[J].软件学报，2009，20(2):271-289.

[11] 郑玉国，袁万城.基于GA-RS的规则钢筋混凝土桥梁圆形单柱桥墩延性抗震优化设计[J].振动与冲击，2010，29(3):81-84.

[12] 柳春光，张士博，柳英洲.基于全寿命抗震性能的近海桥梁结构多目标优化设计方法[J].大连理工大学学报,2015(1)：39-46.

[13] Coello C A C, Pulido G T, Lechuga M S. Handling multiple objectives with particle swarm optimization. Evolutionary Computation[J], IEEE Transactions on Evolutionary Computation, 2004，8(3):256-279.

[14] Wen Y K, Kang Y J. Minimum building life-cycle cost design criteria. I: Methodology[J]. American Society of Civil Engineers, 2014，127(3):330-337.

[15] 中华人民共和国交通运输部.JTG/TB02-01—2008公路桥梁抗震设计细则[S].北京:人民交通出版社,2008.

Life-cycle Seismic Performance Multi-objective Optimization Design of RC Bridge Based on MOPSO

LIU Chunguang, LV Xiaoying, ZHANG Shibo

(FacultyofInfrastructureEngineering,DalianUniversityofTechnology,Dalian,Liaoning116024,China)

In this research, the Multiple Objective Particle Swarm Optimization(MOPSO) was incorporated with response spectrum analysis for the seismic optimization design. The total life-cycle costs were derived by using statistic method, which was based on the maximum displacement angle ratio at the top of the pier under the earthquake of two levels (E1 and E2) by Pushover analysis, and then the minimum cost Pareto solution was obtained. Numerical results indicate that the combination of MOPSO algorithm and response spectrum analysis are highly competitive and can be considered a viable alternative to solve the life-cycle seismic performance optimization problem. The convergence and stability of the algorithm is guaranteed, and the Pareto optimal solutions are distributed uniformity and extensively, which is favourable to the bridge design.

seismic design of single pier; MOPSO; total life-cycle costs; seismic optimization design

10.3969/j.issn.1672-1144.2015.05.001

2015-02-01

2015-03-15

国家重点基础研究发展计划资助“973计划”项目(2011CB013605-4)；国家自然科学基金项目(51178079)；辽宁省优秀人才基金资助项目(2014020012)

柳春光(1964—)，男，黑龙江牡丹江人，博士，教授，博导，主要从事生命线地震工程及城市防灾减灾信息技术方面的研究工作。 E-mail:liucg@dlut.edu.cn

TU375.3

A

1672—1144(2015)05—0001—04