嵌入式筒型结构抗倾稳定性简化计算方法

李彦平，史宏达，吕小龙

(1.中国海洋大学 工程学院，山东 青岛 266100；2.海洋工程山东省重点实验室，山东 青岛 266100)

嵌入式筒型结构抗倾稳定性简化计算方法

李彦平1,2，史宏达1,2，吕小龙1,2

(1.中国海洋大学 工程学院，山东 青岛 266100；2.海洋工程山东省重点实验室，山东 青岛 266100)

针对嵌入式筒型结构在淤泥质海床上的工作机理，建立其在软土地基上的理论计算模型，提出适用于该模型的土压力、摩阻力、地基反力的计算方法，由静力平衡方程，求解得到维持结构稳定的水平极限荷载。通过ANSYS数值模拟软件进行分析，并通过荷载-位移曲线找到结构发生倾覆破坏时的极限荷载，对理论计算进行验证。

嵌入式筒型结构；稳定性；荷载-位移曲线；水平极限荷载

海岸工程建设的迅速发展，导致地质条件优良的海岸线所剩不多，海岸工程开始向深厚软土、淤泥地质等不良地基条件发展。嵌入式筒型结构(或称椭圆形桶形基础结构)是2013年应用于连云港港徐圩港区东防波堤的一种新型结构，对淤泥质海床有良好的适应性，具有广阔的应用前景。嵌入式筒型结构与地基土相互作用复杂，探究其在波浪荷载作用下的抗倾机理尤为重要。对嵌入式筒型结构的物理模型试验已有部分研究成果，徐光明等[1]利用土工离心模型试验分析了该结构在下沉过程中的阻力、筒壁摩擦力及截面压应变随位移的变化；李武等[2-3]利用物理模型试验研究了地基土性质对结构位移及稳定性的影响；高志伟等[4]利用数值模拟的方法探讨了在荷载作用下，不同土层的土压力分布规律。以上研究成果都是基于物理模型试验或者数值模拟分析得到的，而理论计算方面尚无成熟方法。本文将对嵌入式筒型结构进行受力模型分析，探索结构在水平荷载作用下的抗倾稳定机理，进而通过简化的理论计算方法得到结构维持稳定的水平极限荷载。

1 嵌入式筒型结构简介

嵌入式筒型结构由上、下两部分组成，通过混凝土盖板连接在一起。下部是准椭圆形的嵌入结构，类似于倒扣的椭圆沉箱，内有纵横隔舱，顶板上有通气孔；上部可根据实际需要设计成双圆筒、扶壁或沉箱结构。软土封闭在筒仓内，将由盖板传递过来的荷载直接传递给地基，使结构与软土共同承担荷载。下筒、盖板及部分上筒通过预制厂预制，半潜驳运输，负压下沉到位，上筒现场浇注接高。

在水平力的作用下，结构有倾覆和滑移的趋势。此时，下筒一侧产生相对于周围及筒内土向上的位移，此时该侧筒内外壁受到土体向下的摩擦力，相对应的另一侧受到土体向上的摩擦力，两侧土压力共同发挥抗倾作用维持结构稳定；筒体沿外力方向发生水平滑移，背载侧土体受到挤压而产生被动土压力，连同筒底的水平切力共同发挥抗滑作用。

图1 嵌入式筒型结构示意图

2 结构受力分析

嵌入式筒型结构与大直径圆筒结构和负压桶形基础结构类似，属于插入式薄壁筒型结构，在水平荷载作用下，结构绕泥面以下一点转动，发生倾覆破坏[5]。本文忽略波浪荷载的周期性，采用拟静力法进行结构受力分析(图2)。认为在极限波浪力荷载作用下，水平土压力、地基反力、竖向摩阻力均达到极限值，在此情况下主要考虑结构自重G、波浪力P、结构左侧水平土压力PL、右侧水平土压力PR、准椭圆形筒底的水平切力T、垂直反力R和筒内外土体对桶壁的摩擦力f。借鉴大圆筒无锚板桩的计算方法，认为转动点O位于结构的轴心上并距离筒底距离为t处。

图2 结构失稳分析模型

2.1 水平土压力

假设地基土为均质黏土，作用于下筒拱形墙背上的土压力采用朗肯土压力计算，临海侧O点以上为主动土压力区，以下为被动土压力区；临陆侧O点以上为被动土压力区，以下为主动土压力区。采用朗肯土压力理论计算土压力强度及对结构的水平合力和合力矩。

左侧土压力合力为

(1)

式中，α为圆筒墙背土压力折减系数；D为下筒圆形部分外径；H为下筒的高度；h1为转动点到盖板的距离；t为转动点到筒底的距离；kp为被动土压力系数；ka为主动土压力系数；γ为土体重度；c为土体黏聚力。

右侧土压力合力为

(2)

左侧土压力对O点力矩：

(3)

右侧土压力对O点力矩：

(4)

林飘等[6]研究发现，结构倾斜时，仓内土压力基本不发育，接近静止土压力，仓壁两侧土压力关于转动点的力矩抵消，对抗倾没有贡献，因此本文不考虑仓内土压力作用。

2.2 竖向摩阻力

竖向摩阻力是结构在倾覆过程中与土体发生相对位移而产生的摩擦力，主要由土的性质、结构的材料及形状尺寸等决定。

准椭圆形筒壁竖向摩阻力f为

f=τS

(5)

式中，τ为摩阻力强度，单位为N/m2；S为接触面积，单位为m2。结构在波浪力的作用下，发生逆时针转动，认为竖向摩阻力在结构纵向方向上并不相等，而是呈线性分布，结构最左侧竖向摩阻力强度最大，为τmax，右侧摩阻力强度最小，为βτmax。根据美国API规范[7]，粘土中筒型结构的竖向摩阻力最大可取不排水剪切强度cu。

图3 竖向摩阻力在结构纵向上的分布

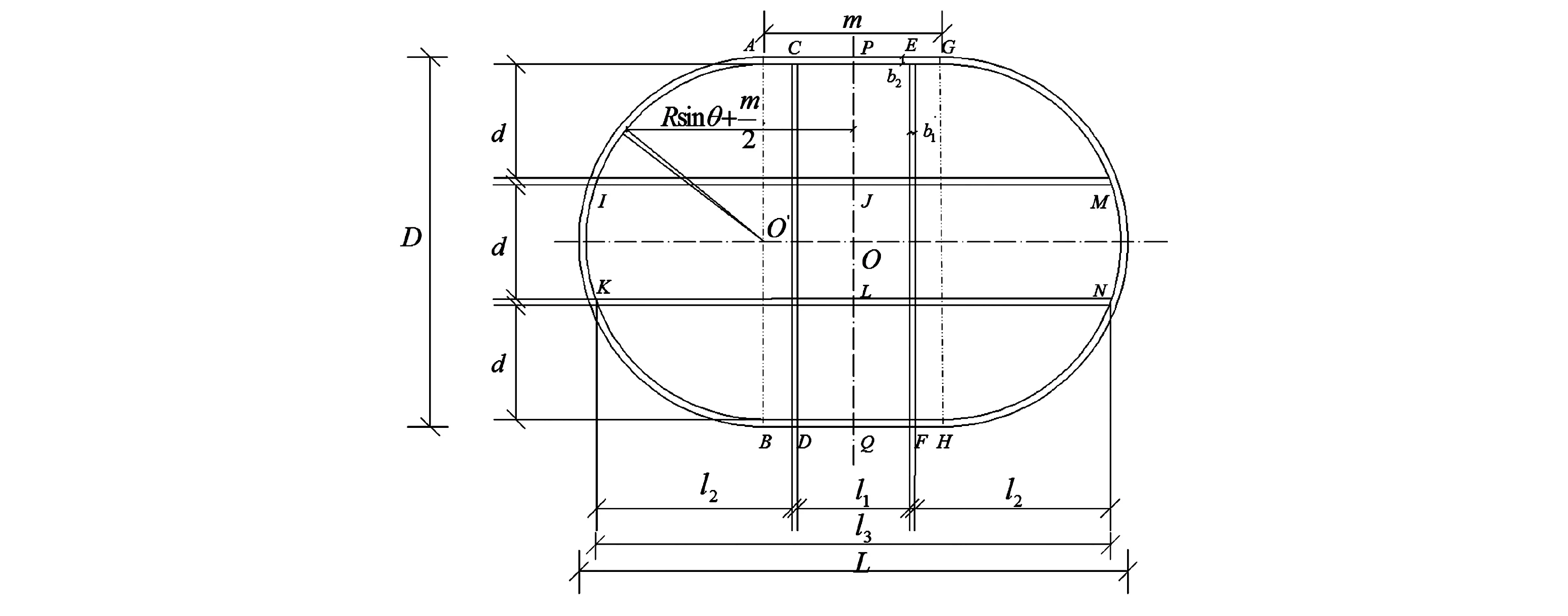
图4 竖向摩阻力示意图

1)弧段AB的摩阻力合力及合力矩为

(6)

(7)

2)CD段的摩阻力合力及合力矩为

f2=2D0Hτ2

(8)

(9)

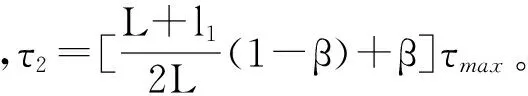
3)EF段摩阻力合力及合力矩为

f3=2D0Hτ3

(10)

(11)

4)IJ和KL段摩阻力及合力矩为

(12)

(13)

5)JM和LN段摩阻力及合力矩为

f5=2(τL+τN)lLNH

(14)

(15)

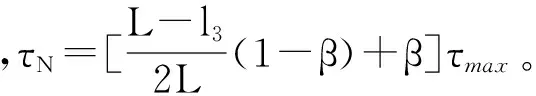
6)AG和BH段摩阻力及合力矩为

(16)

(17)

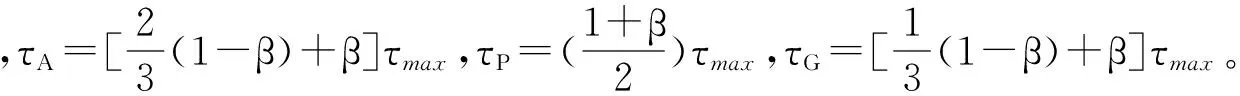
7)弧段GH的摩阻力合力及合力矩为

(18)

(19)

忽略筒壁厚度的影响，认为筒壁上任一点内外摩阻力相等，以向上方向为正，力矩以逆时针方向为正，则摩阻力合力及合力矩为

f=2f1+f2-f3+f4-f5+2f6-2f7

(20)

Mf=-(2M1+M2+M3+M4+M5+2M6+2M7)

(21)

2.3 地基反力

研究发现，筒内土体在竖向力作用下形成的土塞能够使筒内土体没有向外溢出的趋势，地基破坏是筒底及筒外土体屈服后流动的结果。因此认为，地基竖向破坏模式与插入式重力式基础相似[8]，地基反力的表达式为

R=σA

(22)

试验已验证，圆筒结构的地基反力呈直线分布，可以按偏心受压分布计算[9]。本文认为在极限状态下筒底单位面积地基反力σ呈线性分布：左侧筒底地基反力强度最大，为σmax；而右侧筒底即将与地基土脱离接触，地基反力强度为0。

1)弧段AB上的地基反力及对O点力矩为

(23)

(24)

2)CD段上地基反力及对O点力矩为

R2=σ2D0b1

(25)

(26)

3)EF段上地基反力及对O点力矩为

R3=σ3D0b1

(27)

(28)

4)IJ段和KL段地基反力及对O点力矩为

R4=(σK+σL)lKLb1

(29)

(30)

5)JM 和LN段地基反力及对O点力矩为

R5=(σL+σN)b1lLN

(31)

(32)

6)AG和BH段地基反力及对O点力矩为

(33)

(34)

7)弧段GH地基反力及对O点力矩为

(35)

(36)

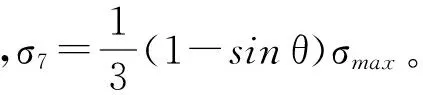
地基反力以向上为正，力矩以逆时针方向为正，结构底部受到地基反力合力及合力矩为

R=R1+R2+R3+R4+R5+R6+R7

(37)

MR=-MR1-MR2+MR3-MR4+MR5-MR6+MR7

(38)

2.4 水平切力

土的抗剪强度是土体抵抗外荷载所产生的切应力的能力，在水平荷载下，筒底土将产生切应力和剪切变形，当土中某点切应力达到抗剪强度时，土就沿着切应力的方向发生相对滑动，即发生剪切破坏。

水平切力可采用下式：

T=Aτf+μR

(39)

式中，A为土体横截面积；μ为结构与土体摩擦系数，根据土体的物理性质确定；R为下筒端部受到的地基反力；τf为考虑了土体黏聚力c的抗剪强度，按下式计算：

τf=σtanφ

(40)

由于下筒端部面积很小，承担的地基反力也小，因此与土体的摩擦力与土层之间的剪切力相比可以忽略，故除了按照上述公式求结构所受的水平切力，API[7]提出了土体水平切力的经验公式：

(41)

式中，cu为黏土不排水抗剪强度。

MT为筒底水平切力对O点力矩，按下式计算：

MT=Tt

(42)

2.5 水平极限荷载求解

采用JTS145-2-2013 《海港水文规范》[10]的要求计算作用在结构上筒的波浪力，可得到设计高水位、波峰时波浪力P及作用点距盖板距离h。考虑海水对结构的浮力作用，结构在平均海平面以下部分，采用浮密度。

根据嵌入式筒型结构受力模型，由水平力平衡条件得：

F1=Pu+PR+T+PL=0

(43)

由竖向力平衡条件得：

F2=G+f+R=0

(44)

对O点的力矩平衡方程：

F3=MPu+∑MPR+∑MPL+MT+∑MR+∑Mf=0

(45)

由式F1，F2，F3建立平衡方程组，共有3个未知量：极限波浪力Pu、转动点与泥面距离t及折减系数β，解方程可得3个未知量的值，从而确定满足抗倾稳定性的最大波浪力值，即水平极限荷载。

3 工程实例

3.1 工程概况

针对连云港港徐圩港区东防波堤的设计方案，利用本文所建立的嵌入式筒型防波堤水平极限荷载求解的简化方法进行稳定性分析，其中h=5.5 m，上筒高度为15.1 m，下筒高度H为10 m,水平面距离盖板为12 m(如图5)。l1=6.3 m，l2=6.2 m，L=30 m，D=20 m，b1=0.3 m，b2=0.4 m(如图4)。

图5 波浪力作用点

工程所在海底区域为第四纪松散堆积层，第一层土体为灰色淤泥，厚度一般为5.2～11.7 m，天然重度为15.8 kN/m3，根据直剪固快试验，内摩擦角8°，黏聚力为8 500 kPa，固结不排水抗剪强度为17.8 kPa；第二层土体为黄褐或草黄色粉质黏土，天然重度为19.3 kN/m3，厚度为2.5～6.5 m，内摩擦角20°，黏聚力为24 kPa，固结不排水抗剪强度为60 kPa。江苏连云港港徐圩港区采用嵌入式筒型结构作为东防波堤，设计要求下筒进入粉质黏土，本文采用下筒恰好接触粉质黏土层的状态进行受力分析计算。

根据F1，F2，F3三个方程，可求得Pu=3.1×107N，t=3.2 m，β=0.87，R=1.6×107N，PL=1.2×107N，PR=6.9×106N，f=2.1×106N。

在工程所在海域，嵌入式筒型结构保持稳定性所能承受的最大的波浪力为3.4×107N，而根据实际水文条件和波浪要素换算得到的波浪力实际值为1.4×107N，证明该结构是稳定的。各抗力对结构稳定的贡献见表1：

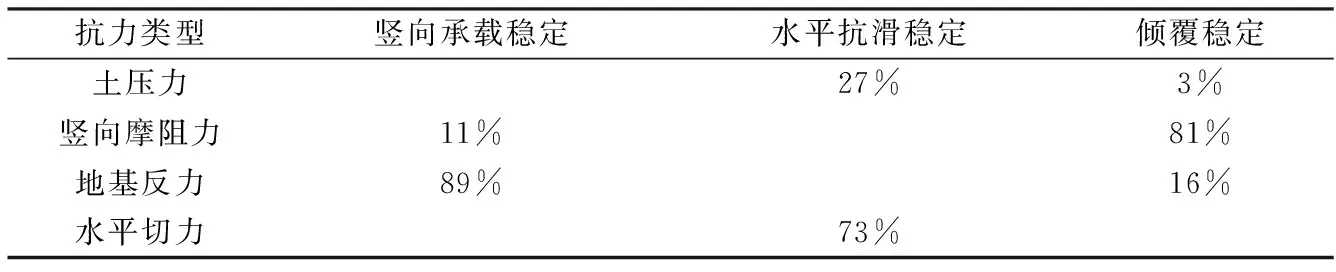
表1 各抗力对结构稳定的贡献 Table 1 Contributions of the resistance forces to the structural stability

注：表中空白处代表未测出

由表1可以看出，地基反力在维持结构竖向平衡中起主要作用，竖向摩阻力的作用比较小，这是因为在结构达到倾覆极限时，转动点两侧的竖向摩阻力方向相反，部分抵消；水平切力在维持结构抗滑稳定中起主要作用，土压力的作用比较小，是因为与结构接触的地基土属于淤泥质软土，又受到海水的浮力作用，重度、内摩擦角及黏聚力都比较小，故其水平土压力比较小；竖向摩阻力在维持结构倾覆稳定中起主要作用，是因为结构下筒内设纵横隔舱，增加了结构与土的接触面积，尽管转动点两侧的竖向摩阻力方向相反，但对O点力矩方向相同，因此竖向摩阻力在维持结构倾覆稳定中发挥了主要作用。

3.2 ANSYS有限元对比验证

采用ANSYS软件建立结构与土的有限元计算模型，土体采用Drucker-Prager模型，采用solid45单元。结构采用线弹性模型，采用solid63单元，结构与土的相互作用采用刚性体—柔性体的面面接触单元，有限元模型相关参数见表2：

表2 结构与土体参数 Table 2 Parameters of the structure and the soil mass

注：表中空白处代表未测出

作用在上筒的波浪力采用集中力的方式加载，上筒的波浪力合力从12 000 kN增加到46 000 kN，得到结构在水平荷载作用下的荷载-位移曲线，如图6：

图6 荷载-位移曲线

图6中黑色曲线为荷载-位移的10阶多项式拟合曲线，从图中可看出，当集中力从1.2×107N开始增大时，结构最大位移先呈线性增加，当荷载增加到3.2×107N时，曲线斜率明显变大，认为结构开始达到极限状态。所以，根据ANSYS有限元模拟得到的水平极限承载力为3.2×107N，这与理论计算结果比较接近，能够较好地证明理论计算方法的可行性。

4 结 语

本文从理论计算的角度对嵌入式筒型结构的抗倾稳定性进行了研究，主要结论如下：

1)本文提出的嵌入式筒型结构稳定性计算的方法，适用于软土地基，结构主要依靠被动土压力和筒底摩擦力维持抗滑稳定，主要依靠地基反力和竖向摩阻力维持竖向稳定，依靠上述抗力对转动点的力矩维持倾覆稳定性。

2)结构下筒内设纵横隔舱，不仅增加了结构的强度，还增加了结构与土的接触面积，从而增加了土对结构的竖向摩阻力，使结构在波浪荷载作用下更加稳定。

3)文中计算方法针对的是均匀土质，也可用于多层土质的情况，只需分层计算土压力、摩阻力等即可。

目前嵌入式筒型结构的研究相对较少，本文认为应从如下角度继续深入研究：

1)波浪作用是循环往复荷载，本文采用拟静力法对结构平衡进行分析，忽略了在波浪连续作用下，结构累计变形的的影响。因此，考虑波浪作用下，结构与土的动力本构关系分析是有待研究的课题。

2)嵌入式筒型结构在淤泥质海床上的工作机理比较复杂，且结构失稳过程并非静态，虽然本文提出的理论模型考虑因素较全，但并无大量的工程实例验证。因此，还需要针对其他工程实例进行验证，并结合ANSYS数值模拟软件进行分析。

[1] 徐光明,顾行文,任国锋,等.防波堤椭圆形桶式基础结构的贯入受力特性实验研究[J].海洋工程,2014,32(1):1-7.

[2] 李武,陈甦,程泽坤,等.水平荷载作用下桶式基础结构稳定性研究[J].中国港湾建设,2012,(5):14-18.

[3] 李武,吴青松,陈甦,等.桶式基础结构稳定性试验研究[J].水利水运工程学报,2012,(5):42-46.

[4] 高志伟,陈甦,李武,等.桶式基础结构土压力分布规律[J].中国港湾建设,2013,(1):18-21.

[5] MURFF J D, HAMILTON J M．P-ultimate for undrained analysis of laterally loaded piles[J].Journal of Geotechnical Engineering,1993,119(1):91-107.

[6] 林飘,姚文娟,张峻,等.筒式基础结构分仓形式对抗倾承载力的影响[J].中国港湾建设,2013,(6):30-35.

[7] American Petroleum Institute. Recommended practice for planning, designing and constructing fixed offshore platforms[S].Washington: API Publishing Services, 2000.

[8] 刘振纹.软土地基上桶形基础的稳定性研究[D].天津:天津大学,2002.

[9] [苏]C.H.列瓦切夫.薄壳在水工建筑中的应用[M].赵诩，向可钦，译.北京:人民交通出版社,1982.

[10] JTS145-2-2013 海港水文规范[S].北京:人民交通出版社,2013.

A Simplified Calculation Method for Anti-Overturn Stability of Embedded Cylindrical Structure

LI Yan-ping1，2, SHI Hong-da1，2, LÜ Xiao-long1，2

(1.CollegeofEngineering,OceanUniversityofChina, Qingdao 266100, China; 2.TheKeyLaboratoryofOceanEngineeringofShandongProvince,OceanUniversityofChina, Qingdao 266100, China)

A theoretical calculation model is established for the structure built on the soft-soil foundation according to the working mechanism of embedded cylindrical structure on the muddy seabed, and methods for calculating the soil pressure, friction resistance and subgrade reaction suitable for the model are proposed. The horizontal ultimate load to sustain the stability of the structure is obtained by solving with the equation of static equilibrium. Through the analysis by using ANSYS numerical simulation software and the load-displacement curve, the ultimate load that makes the structure overturn and destroy can be found out and the theoretical calculation model is verified.

embedded cylindrical structure; stability; load-displacement curve; horizontal ultimate load

1002-3682(2015)03-0044-11

2015-01-21

李彦平(1989-)，男，硕士研究生，主要从事港口、海岸及近海工程方面研究. E-mail：yanping_ouc@163.com(张 骞 编辑)

TU411

A