间隔阈值的多元经验模态分解电磁信号去噪

李 端，张洪欣，李 强

（1. 北京邮电大学电子工程学院，北京 100876； 2. 河南理工大学电气工程与自动化学院，焦作 454000；3. 北京邮电大学北京市安全生产智能监控重点实验室，北京 100876）

间隔阈值的多元经验模态分解电磁信号去噪

李 端1,2，张洪欣1,3，李 强1

（1. 北京邮电大学电子工程学院，北京 100876； 2. 河南理工大学电气工程与自动化学院，焦作 454000；3. 北京邮电大学北京市安全生产智能监控重点实验室，北京 100876）

传统小波分解去噪需要先验知识，缺乏自适应性，将多元经验模态分解间隔阈值（Multivariate Empirical Mode Decomposition，MEMD）滤波方法用于电磁泄漏信息预处理。首先对电磁泄漏信号进行对齐处理。然后，针对多元经验模态分解直接阈值滤波产生的不连续性问题，提出采用MEMD间隔阈值滤波方法进行不相关模态滤波，解决传统经验模态分解的模态混叠问题。最后，分别采用巴特沃斯低通滤波、小波阈值、MEMD-DT和MEMD-IT方法对密码芯片电磁泄漏数据进行去噪处理，通过基于最小二乘支持向量机分类识别，实验结果表明该自适应去噪方法的优于传统的电磁侧信道分析预处理方法。

电磁侧信道分析；多元经验模态分解；间隔阈值去噪；最小二乘支持向量机（LSSVM）

引言

电磁分析（Electromagnetic Analysis, EMA）是通过测量芯片在运行过程中的电磁辐射信号，研究电磁辐射与内部操作数和指令之间的相关性而获取密钥。电磁模板分析主要依靠与密钥相关的指令操作的泄漏信息，进行模式分类识别[1-5]，所以信号采集过程中的内部和外部噪声将大大影响最终的识别效果。电磁信号采集过程中易受外界噪声、接收设备内部噪声以及密码设备运行时的内部噪声等干扰，而且不同的加密设备、算法实现和测试设备所引入的噪声差异较大。有效的自适应信号预处理方法是电磁侧信道分析的关键。

文献[6～7]采用电磁泄漏信号的大样本均值来消除噪声，这样会大大增加样本量。Messerges等人提出简单滤波改善信噪比和改进的DPA攻击方法来改善信号的信噪比[8]。文献[9]提出侧信道分析数据预处理阶段采用四阶累积量方法增强了信噪比，减少了侧信道分析的样本量。而高阶统计量对加性高斯噪声不敏感，需要大量的统计数据和较大的计算量。

经验模态分解方法克服了小波分解、傅里叶变换等需要先验知识的缺点。该方法是完全自适应于信号，具有多分辨分析和完全重构的特性，取消了小波分解的窗函数作用，具有完全的局部时域特性，是一种更精确的电磁信号分析和去噪方法，比较适合非平稳、非线性信号的分析和降噪处理[10]。Flandrin等人提出经验模态分解方法对分形高斯噪声消噪效果明显优于小波处理[11]。

由于侧信道模板攻击是多分类问题，为了使不同类别的信号分解时具有同一尺度，而且克服经验模态分解的模态混叠现象，提出将间隔阈值多元经验模态分解（MEMD）去噪方法用于电磁辐射信号的自适应去噪。首先，分析了多元经验模态分解阈值去噪方法并进行了信号仿真比较，然后用该方法对实验采集的电磁泄漏信号进行自适应去噪，最后通过最小二乘支持向量机电磁分析评估了所提方法的效果。

1 多元经验模态分解去噪方法

多元经验模态分解将N 元时间序列看作N维向量序列，在N维空间中沿不同方向投影向量序列，计算各个投影向量的包络。求这些包络的均值即为多元时间序列的均值向量，尽而实现多元信号同尺度分解[12]。

经验模态分解得到的模态分量的频率段随着模态阶数的增大而减小。通常阶数低的模态频率高，含有原信号的尖锐和噪声成份，反之阶数高的模态分量包含有用信号的主要能量[13]。合理有效地找出噪声模态和信号模态的分界点是滤波的关键技术之一。

1.1 相关模态选择标准

假设用 ()y t表示无噪声观测信号， ()n t表示白噪声，()x t表示原始含噪信号,去噪后的信号估计值为˜()x t，则MEMD去噪的部分重构方法可表示为：

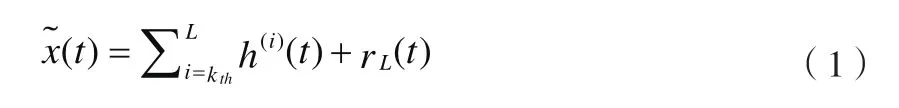
用相关系数法即原始信号 ()x t和部分模态的相关系数估计出临界值thk，为计算方便，方程（1）也可表示为：

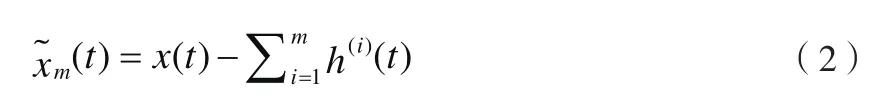
其中， =th-。

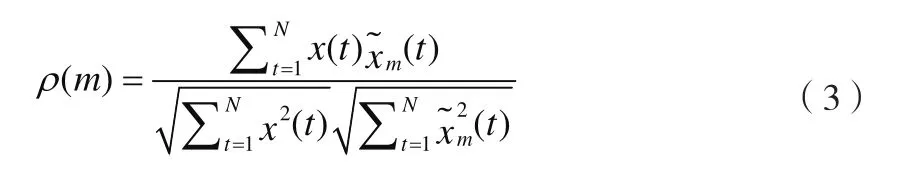
其中，N为数据长度，当 ρ( m)开始小于常数C时，即可计算出分界点 kth，一般取 C∈ [0.75,0.85]，本文中取C=0.8。因此 kth可表示为：

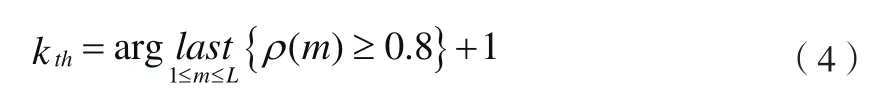
1.2 间隔阈值去噪方法

按照上述方法选择thk ，由表达式（2）可实现部分重构去噪。但是在信噪比（SNR）较高时，有用观测信号往往被分解到低阶不相关模态中，直接部分重构方法去噪会损失有用成份。为提升部分重构方法的性能，选择对不相关模态分量进行阈值滤波后整体重构。

1.2.1 阈值选择依据

阈值是用于控制偏差和方差交替变化风险的参数。阈值过小，估计值会造成信号的过拟合，结果将十分接近输入信号；如果阈值过大，一些模态值将会被设置为零，会造成信号欠拟合，估计方差减小而偏差增大。本文中使用噪声水平来选择阈值，由于该测试信号含有高斯白噪声，此阈值取决于每个模态的白噪声能量。根据高斯噪声的特性[14]，其统计特性由Hurst指数H来确定，经EMD分解之后的各阶模态中的高斯噪声能量按指数递减，可定义为：

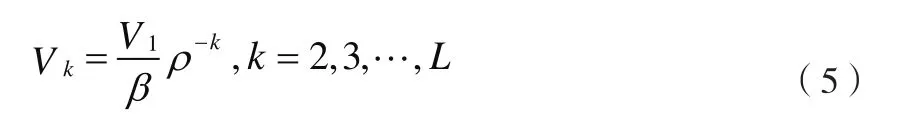
其中，1V是噪声能量，噪声标准差可根据第一模态分量估计出，结果如下：

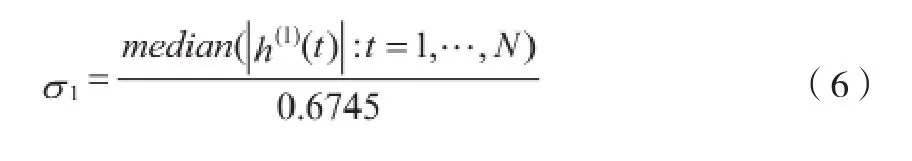
文献[15]中，Flandrin et al.经大量实验提出β和ρ比较合适的取值分别为0.719和2.0。

每个模态的自适应阈值可由下式确定：

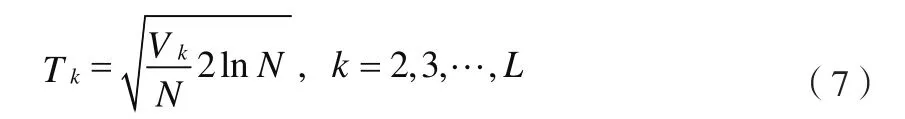
其中，N为信号长度。

1.2.2 间隔阈值去噪

由于EMD分解之后的各模态与零均值的正弦调制信号相似，即使无噪声纯净信号被分解之后，临近过零点处的值也会小于阈值，被误认为噪声。因此传统的直接阈值去噪不够精确，而且会导致重构信号的不连续性。

经验模态分解间隔阈值去噪包括硬阈值去噪和软阈值去噪，去噪之后信号˜()x t可表示为：

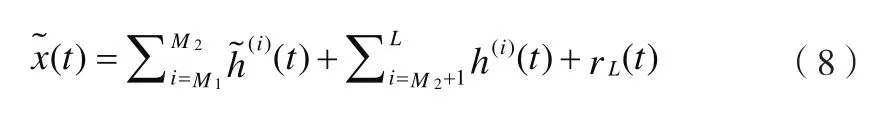
如果用硬阈值去噪，则

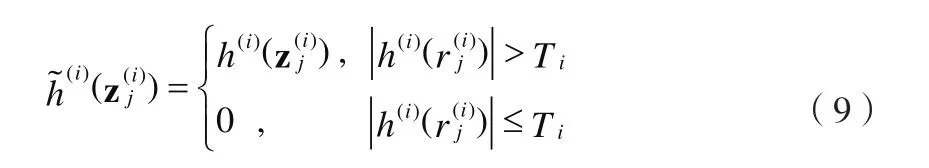
软阈值滤波函数可表示为：

公式（8）中的变量 M1和 M2可根据不同的相关模态选择方法和实际情况灵活选择， Ti对应第i阶模态的值。由公式（8）～（10）实现的滤波方式叫做间隔阈值EMD去噪，其中， h(i)()表示第i阶模态两个临界过零点和之间的所有样本点， h(i)()表示此间隔内的极值。

以随机信号经验模态分解的IMF4为例，分别选择直接和间隔阈值去噪，图1(a)和(b)分别表示直接和间隔阈值去噪结果示例，直接阈值去噪在阈值之内的点被置零，如图1(a)有很明显的间断，(b)图所示滤波后则保持了该模态的平滑性。

2 密码芯片电磁分析数据预处理

2.1 电磁泄漏信号采集及对齐

本节针对8位长度密钥的RC4密码算法进行模板攻击实验，STC89C52单片机运行加密算法并且触发示波器采集，晶振频率为11.059 2 MHz，示波器采样频率500 MHz。RC4加密算法采用随机密钥输入，采集7200条电磁辐射能量迹。为保证微控制器每次加密的电磁泄露是严格对齐的，即同一时刻控制器执行相同的操作，需对采集的信号进行对齐处理。选择密码芯片刚开始加密时（即示波器刚开始触发）的一段电磁泄漏作为模式，用最小二乘算法进行模式匹配，实现信号的对齐。

2.2 电磁泄漏信号去噪

2.2.1 密码芯片电磁辐射噪声机理分析

电磁信号的采集容易受噪声干扰，在实际的测试中，电子装置所产生的所有波动电流和电压会引起噪声，这种噪声的概率密度函数都符合高斯分布[9]。这些波动量是大量独立随机变量的总和，这些内部噪声都可认为是高斯噪声。另外还有加密芯片自身存在算法噪声(与所攻击的中间值无关的指令操作所泄露的电磁信号)、转换噪声和电子噪声，这类噪声也可看作高斯噪声。

2.2.2 间隔阈值MEMD去噪实验结果分析

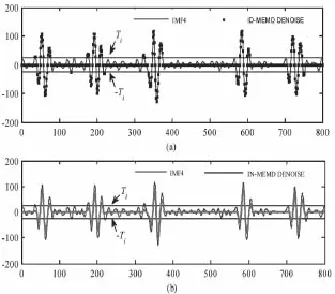
图1 直接和间隔阈值去噪

选择RC4加密算法密钥扩展阶段的电磁泄漏数据，图2给出了三种汉明重密钥的部分电磁样本点。图中包含原始信号、模式匹配对齐之后的曲线以及滤波之后的结果。从图中可以看出，滤波之后得到较平滑的周期震荡信号，每个周期幅值有较小差异，这正是与执行不同秘密信息相关的特征体现。

3 电磁侧信道分析实验评估

密码设备运行一次过程中采集到的时域电磁辐射信号为一条样本曲线，它是由时间域多个离散的点组成。过高的维数难以被机器学习算法有效地处理。基于机器学习的侧信道分析主要是提取与秘密信息（密钥的汉明重）相关的数据点。本实验采用Pearson相关法提取与汉明重相关的特征点。公式（11）中，cov(·,·)表示协方差，var(·,·)表示方差， x( t)代表电磁能量迹，y代表假设能量消耗（对应原始密钥的汉明重）。如果原始数据位数用N表示，可得到相关系数向量 ρ=[ρ(1),ρ( 1),… ,ρ(N )]，选择不同的阈值，根据相关系数不同取值范围可得到不同数量的特征点。

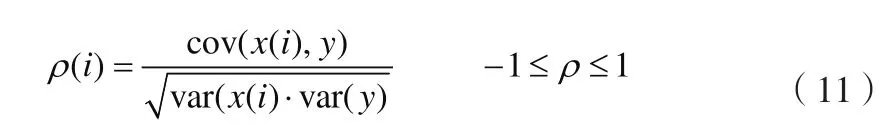
机器学习法进行密钥汉明重量识别的效果取决于在一定相关系数值下，所提取的特征点个数。本实验随机选择密钥汉明重分别为0～8的电磁曲线各200条，共1800条，截取密钥扩展阶段电磁泄漏的10万样本点，用相关法对密钥字节的9种汉明重量进行特征提取，提取的特征作为机器学习的样本。分别采用80 Mhz截止频率的巴特沃斯低通滤波、小波无偏似然估计阈值、小波固定阈值去噪和MEMD直接、间隔阈值去噪方法对数据进行预处理，其中小波去噪时用db5小波函数进行3层分解。表1列出了对应相关系数阈值所提取的特征点数。机器学习9分类实验结果表明，在 0.65ρ≥ 且特征点数大于70个时，分类识别正确率达到了87 %，随着特征点数和ρ的减小，分类成功率都有所下降。从表1中可看出，IN-MEMD 提取出较多特征点，其次是小波固定阈值去噪，巴特沃斯低通滤波在不同截止频率下效果差异较大，不具有滤波的自适应性。

图2 电磁泄漏信号预处理

表1 不同相关系数和滤波方法所提取的特征点数

为了证明所提取特征点的效果，以2790条电磁泄漏曲线为例，其中2250条作为训练样本，450条作为测试样本。对密钥扩展阶段电磁泄漏20万样本点用间隔阈值自适应去噪，然后提取相关系数大于0.65的特征点120个，SVM训练并测试，最终分类准确率达到了91.666 7 %。

4 总结

数据的去噪等预处理是电磁模板分析的关键，通过分析密码芯片电磁辐射的噪声机理及模板分析的实质，根据噪声的本质特性，将非参数MEMD的自适应滤波方法用于电磁侧信道分析。实验表明该自适应去噪方法能有效去除噪声，尽而有效提取与密钥汉明重相关的数据点，为秘密信息汉明重的识别率和密钥的搜索提供了有力保障。

[6] Chari, S, Rao, et al, Template Attacks . CHES 2002, LNCS 2523：172-186.

[7]李佩芝.分组密码芯片模板攻击关键技术研究[D]： [硕士学位论文].河南：解放军信息工程大学, 2013.

[8] T.S.Messerges, E.A.Dabbish, R.H.Sloan. Examining smart-card security under the threat of power analysis attacks. IEEE J.Comp ut.,vol.51,no.5,pp：541-552,2002.

[9] Thanh-Ha Le, Jessy Clediere,Christine Serviere et al.Noise Reduction in side Channel Attack Using Fourth-Order Cumulant[J].IEEE Transactions on information forensics and security, 2007(2)：710-720.

[10]贾守卿,江小敏,夏明耀.基于微多普勒特征的目标分类[J].电波科学学报, 2013,28(3)：443-447.

[11] P.Flandrin,G.Rilling, P.Goncalves.”EMD equivalent filter banks, from interpretation to applications,” in Hilbert-Huang Transform and Its Applications,N.E.Huang and S.Shen,Eds.,1st ed.Singa-pore：World Scientif c,2005.

[12] Komaty.A, Boudraa.AO,et al. On the Behavior of EMD and MEMD in Presence of Symmetric alpha-Stable Noise. IEEE Signal Processing Letters, 2015, 7(22)： 818-822.

[13] Wu Z,Huang N E. Ensemble empirical mode decomposition： a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis(S1793-7175),2009,1(1)：1-41.

[14] 曹冲锋,杨世锡,杨将新. 大型旋转机械非平稳振动信号的EEMD降噪方法[J].振动与冲击, 2009,28(9)： 33-38.

[1] Lerman L, Bontempi G, Markowitch O. Side channel attack：an approach based on machine learning. Center for Advanced Security Research Darmstadt, 2011：29-41.

[2] Hospodar G, Gierlichs B, De Mulder E, et al. Machine learning in side-channel analysis： a first study. Journal of Cryptographic Engineering , 2011,1(4)：293-302.

[3] Martinasek Z, Zeman V. Innovative Method of the Power Analysis. Radio engineering, 2013,22(2)：17-20.

[4] Zeng Zhong, GuDawu, Liu Junrong, et al. An improved Side-Channel Attack Based on Support Vector Machine. 2014 Tenth international Conference of Computational intelligence and Security： Sep21-25, 2014：676-680.

[5]刘飚,封化民,袁征,等.一种针对密钥的单比特电磁模板攻击方法[J].电波科学学报, 2012,27 (6)： 1213-1218.

Noise Reduction in Electromagnetic Emanation Using MEMD Interval Threshold

LI Duan1,2, ZHANG Hong-xin1,3, LI Qiang1
（1. School of Electronic Engineering, Beijing University of Posts and Telecommunications, Beijing 100876；2. School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454000；3. Beijing Key Laboratory of Safety Production and Intelligent Monitoring, Beijing 100876）

To overcome the dependence of prior knowledge and non-adaptive of traditional filtering algorithm, a Multivariate Empirical Mode Decomposition interval threshold (MEMD-IT) de-noising which is a nonparametric signal de-noising approach is presented as a preprocessing stage for electromagnetic radiation signals. First, the near field electromagnetic leakage signals were captured while cipher device was executing RC4 algorithm. MEMD-IT is developed which can reduce the discontinuity induced by EMD-DT. Comparing with the other filters, such as Butterworth low-pass filter, wavelet threshold denoising, and MEMD direct threshold (MEMD-DT) de-noising, the proposed de-noising method evaluated by the Hanming weight classification results based on LSSVM has a better performance.

electromagnetic side-channel attack; multivariate empirical mode decomposition (MEMD); interval threshold de-noising; least-squares support vector machine (LSSVM)

TN918/TP393.08

A

1004-7204（2015）04-0060-05

国家自然科学基金（61202399,61171051）

李端，女，河南南阳，北京邮电大学博士研究生，副教授，研究方向：微弱信号处理，电磁兼容。