基于模糊层次分析法的投资项目评估

侯春梅

(天津万泽建设工程咨询有限公司, 天津 300050)



基于模糊层次分析法的投资项目评估

侯春梅

(天津万泽建设工程咨询有限公司, 天津 300050)

结合投资估算精度的特点，采用模糊层次分析法，建立模糊判断矩阵并判断其一致性；针对投资估算问题的复杂性和模糊性，建立投资估算精度影响因素模糊综合评价模型，并结合实例对投资估算精度进行模糊综合评价，以期为改善投资估算精度提供参考。

模糊层次分析法；模糊判断矩阵；模糊综合评价；投资估算精度

在项目投资估算时，编制人员的估算具有很强的模糊性，难以合理保证投资估算精度要求。投资估算的许多因素及总体评价都是相对而言的，其本身没有精确定义的判别准则，具有模糊性，而模糊数学正是研究这种模糊现象的较为恰当的处理方法。基于此，可把模糊层次分析法引入投资估算应用，利用模糊层次分析法可以使结果更为全面、深入、细致，更符合客观实际，最终实现对投资估算的精度分析。

1 模糊层次分析法的特点

1.1 模糊判断矩阵

模糊判断矩阵R是将下层元素{a1,a2,…,an}相对于上一层元素的重要性两两比较，得到相对重要性模糊矩阵R：

其中，rij(i,j∈(1,2,…,n))为下层第i个元素相对于第j个因素具有模糊关系。

模糊矩阵R=(rij)n×n满足rij+rji=1(i=1,2,…,n;j=1,2,…,n)时则为模糊一致矩阵[1]。

1.2 模糊判断矩阵的一致性

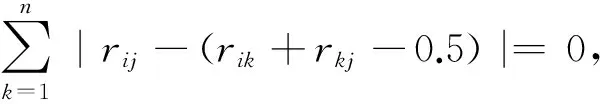
基于以上分析，可用指标ρ来表示R的不一致性程度：

由于rji=1-rij，因此有：

模糊判断矩阵R为模糊一致矩阵的充要条件是ρ=0。

1.3 应用步骤

(1)建立因素集。根据投资项目的特点，确定影响投资估算精度的因素，构成因素集：X=(X1，X2，…，Xn)，其中，Xi为该投资项目对估算精度有影响的第i个因素。

(2)建立评估集。可根据其实际细分程度及计算量大小设定。将定性指标分为合适的几个档次，定量指标也分为合适的几个档次。由专家小组成员对于各指标按照评语级别标准进行评价，建立每个档次与隶属度之间的关系。

(3)确定评价矩阵。对因素集中的单因素集作单因素评判，确定该因素对选择等级的隶属度，即得出单因素评判集RXi=(ri1,ri2,…,rin)。RXi是评语集V上的模糊子集，这样n个因素的评价集构造出一个总的评价矩阵RX′为：

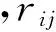
(4)模糊综合评价。采用模糊综合评价综合考虑所有因素的影响，以得出正确的评价结果。

2 应用分析

2.1 投资估算作用

投资估算是进行投资方案选择的重要依据之一，同时也是主管部门进行项目审批的参考依据。具体而言，投资估算的作用包括：在项目建议书阶段，投资估算是项目主管部门审批项目建议书的依据之一；在项目可行性研究阶段，投资估算是项目投资决策的重要依据，也是研究、分析和计算项目投资经济效果的重要条件；在设计招标中，投资估算是优选设计单位和设计方案的重要依据。投资估算也是实行限额设计的依据，还可以作为项目资金筹措及制订建设贷款计划的依据，建设单位根据批准的投资估算额进行资金筹措和向银行贷款；投资估算是核算建设项目固定资产投资需要和编制固定资产投资计划的重要依据。

投资估算精度不仅影响可行性研究工作的质量和经济评价效果，而且也直接关系到设计概算和施工图预算的编制，对建设项目资金筹措方案也有直接的影响。因此，投资估算精度对项目的规划、规模起重要参考作用。

2.2 投资估算精度影响因素

对投资估算精度的影响因素，不同的学者给出了不同的见解，综合一些学者的观点，影响投资估算精度的因素包括法规因素、环境因素、技术因素、人员因素和经济因素等5个方面，具体如图1所示。其中，目标层为投资估算精度影响因素，准则层为法规因素、环境因素、技术因素、人员因素和经济因素。

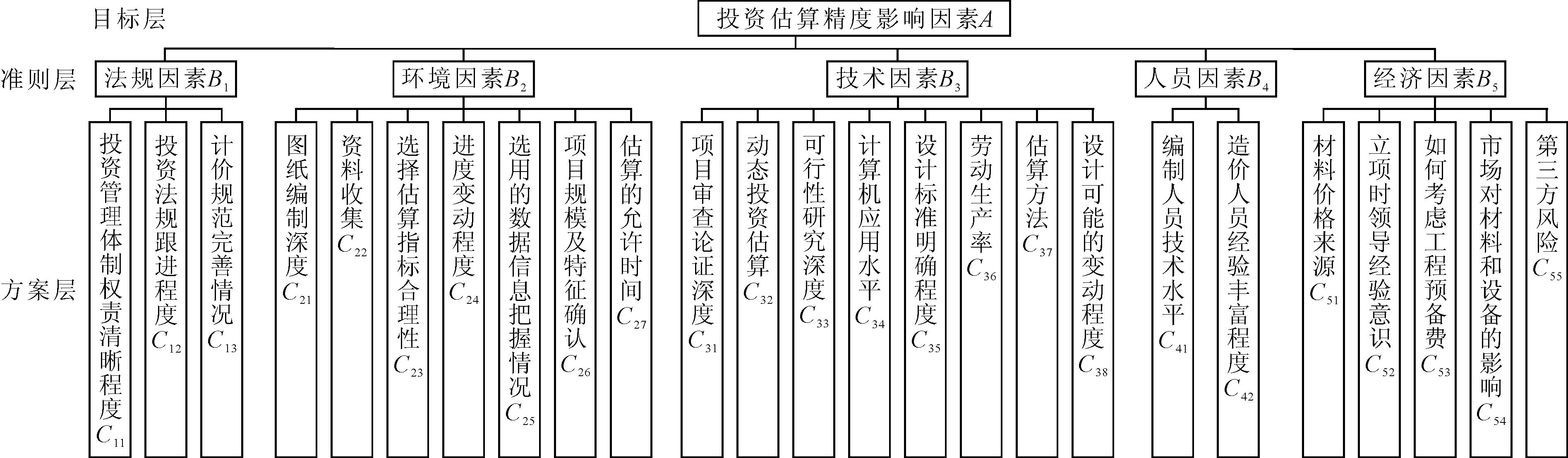
图1 投资估算精度影响因素模糊综合评价图(根据文献[3-10]整理)

2.3 实证分析

某项目总建筑面积14 254m2，其中地下室面积为2 470m2；地下1层，地上7层，建筑面积11 784m2，主体檐口高度为30.6m；基础采用灌注桩，结构形式为框架结构。最终该项目实际投资9 000万元，项目报批时建设单位编制的报投资部门的投资估算为8 600万元。现对该项目的投资估算进行模糊综合评价。

该项目模糊综合评价过程如下：

(1)方案层模糊计算过程。建立B-C模糊判断矩阵，具体如表1～表5所示。

对于法规因素，经计算可知：λmax=3.018，CI=0.009，RI=0.580，CR=0.016。

表1 法规因素模糊判断矩阵

表2 环境因素模糊判断矩阵

对于环境因素，经计算可知：λmax=7.500,CI=0.083,RI=1.320,CR=0.063。

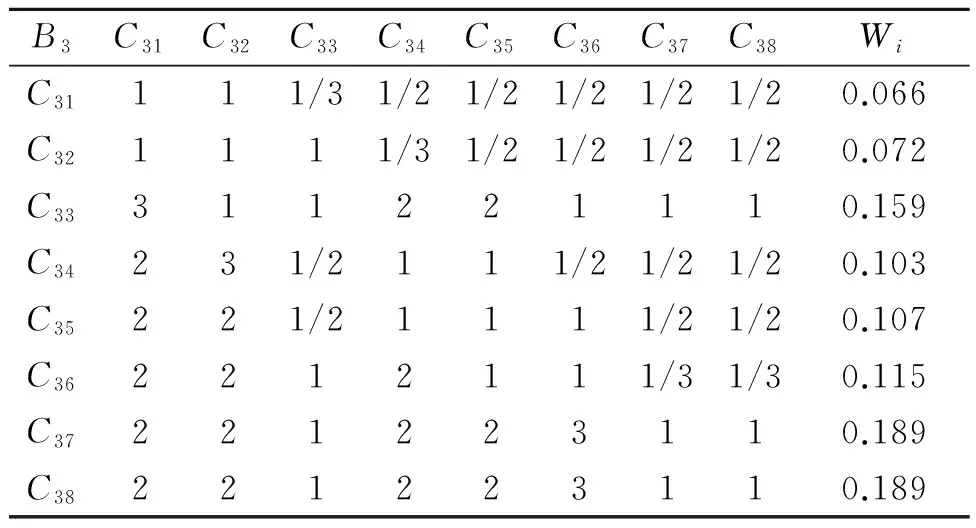
表3 技术因素模糊判断矩阵

对于技术因素，经计算可知，λmax=8.429，CI=0.061，RI=1.410，CR=0.043。

表4 人员因素模糊判断矩阵

经计算可知，λmax=2，CI=0，RI=0，CR=0。

表5 经济因素模糊判断矩阵

经计算可知，λmax=5.037，CI=0.009，RI= 1.120，CR=0.008。

(2)准则层模糊计算过程。

B1=(0.625,0.238,0.136)×

(0.508,0.352,0.138,0)

B2=(0.163,0.236,0.202,0.123,0.081,

(0.592，0.275，0.107，0.025)

B3=(0.066，0.072，0.159，0.103，0.107，0.115，

(0.552,0.288,0.125,0.036)

(0.550，0.300，0.150，0.000)

B5=(0.168，0.321，0.106，0.038，0.366)×

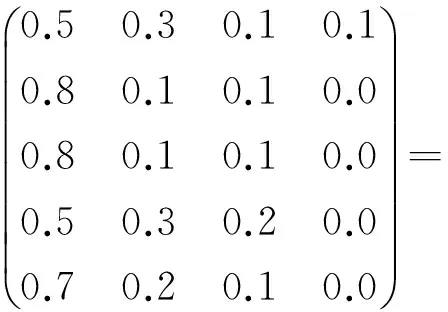
(0.701，0.178，0.104，0.017)

(3)目标层模糊计算过程。建立A-B模糊判断矩阵，具体如表6所示。

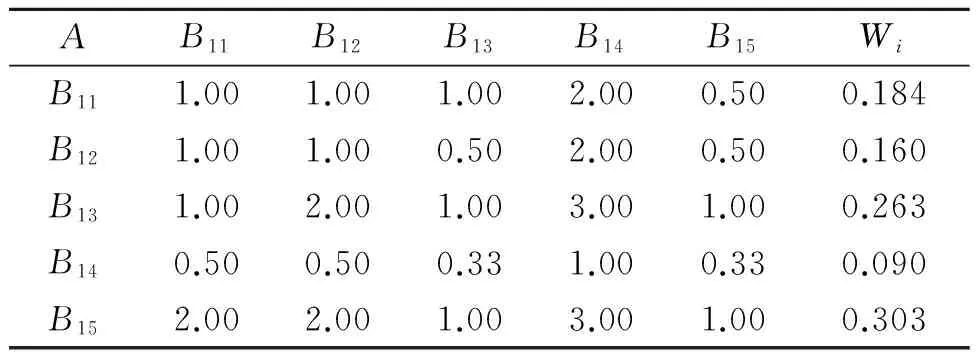
表6 准则层模糊判断矩阵

经计算可知：λmax=5.055，CI=0.014，RI=1.120，CR=0.012。

A=(0.184，0.160，0.263，0.090，0.303)×

(0.595，0.265，0.121，0.019)

(4)模糊综合评价结论。根据模糊综合评价结果，由模糊分布原理可知，59.5%的人认为该投资估算为优，26.5%的人认为该投资估算为良，12.1%的人认为该投资估算为中，1.9%的人认为该投资估算为差。

为使综合评价具有可比性和直观性，将评价集“优”、“良”、“中”、“差”分别赋值90、80、70、50。划分评价区间:[80,90]为“优”；[70,80)为“良”；[50,70)为“中”；[0,50)为“差”。结合上述评价方法，可以使综合评价指标量化，经计算综合评价得分为90×0.595+80×0.265+70×0.121+50×0.019=84.195，因此，该项目投资估算综合水平属于优。

(5)结论分析。从模糊向量单值化的结果来看，最终评价分数为84.195分，说明该项目编制的投资估算质量属于较高水平，以该投资估算作为决策依据，可以指导决策者控制投资。若在决策过程中编制了多份投资估算，还可以对所编制的投资估算质量进行由高到低排序，让决策者采纳编制质量最好的投资估算，防止由于投资估算不准确而导致最终决策失误的风险。因此，在项目可行性研究时，应注重对投资估算编制的评价。

2.4 提高投资估算精度措施

投资估算误差在所难免，但采取一定措施可以提高投资估算精度，将误差率控制在决策允许范围内，具体措施包括：认真搜集、整理和积累各种建设项目的造价资料，建立资料积累数据库，实现信息网络化，使其具有更大的参考价值；灵活运用工程造价资料和技术经济指标，切忌生搬硬套；预留适度的预备费；提高估算人员的综合水平。综上所述，加强法规因素、环境因素、技术因素、人员因素和经济因素等方面的预控机制，有助于提高投资估算精度。

3 结论

项目如果仅仅考虑财务上的可行，而不注重项目的投资估算，会导致“钓鱼工程”、“三超”现象项目的产生[11]。通过对模糊层次分析法的研究，把该理论方法运用到对建设项目投资估算精度综合评价。采取合理措施提高投资估算精度，在满足精度要求的基础上进行项目决策，不仅可减少投资失误，还可实现建设资金的“资源优化配置”，提高建设资金的使用效率。

[1] 张吉军.模糊层次分析法[J].模糊系统与数学,2000(6)：82-90.

[2] 陈均明.模糊层次分析法在投资决策中的应用[J].重庆工商大学学报，2008(2)：33-36.

[3] 张效慧,李晓波,衣建军.严格投资估算控制项目投资[J].黑龙江金融，1997(3):56-57.

[4] 解军胜.设计阶段投资估算准确性探析[J].今日科苑，2009(7)：108-109.

[5] 李海深，桂林霜.谈投资估算的准确性[J].山东省农业管理干部学院学报，2003(5):81-82.

[6] 虞亚敏.谈可行性研究投资估算的准确性[J].有色金属设计，1995(1):73-76.

[7] 柯德玉.浅谈水利工程投资估算的编制与问题[J].福建建筑，2009(4):88-89.

[8] 杜一男，吴剑刚.长输管道建设项目投资估算准确性因素分析及建议[J].石油规划设计，2010(1):18-19.

[9] 岳云伏,尹益才,邵丽华.投资估算风险分析[J].中国海上油气工程，1999(4):60-63.

[10] 付发明.建设项目投资估算研究[D].成都：西南交通大学，2014.

[11] 徐良德.基于模糊理论的建设项目投资估算影响因素研究[D].成都：西华大学，2010.

HOU Chunmei:Engineer; Tianjin Wanze Constructive and Engineering Consult CO., LTD, Tianjin 300050, China.

[编辑：王志全]

Evaluation on Investment Project Based on Fuzzy Analytic Hierarchy Process

HOUChunmei

Based on the analysis of fuzzy analytic hierarchy process, a fuzzy judgment matrix was established and its judgment consistency was tested. For the complexity and fuzziness of investment estimation problem, a fuzzy comprehensive evaluation model was present for factors affecting the accuracy of investment estimation. The fuzzy comprehensive evaluation was presented combining with example. It provides reference for improvement on investment estimation accuracy.

fuzzy analytic hierarchy process; fuzzy judgment matrix; fuzzy comprehensive evaluation; investment estimation accuracy

2015-03-21.

侯春梅(1979-)，女，河南新乡人，天津万泽建设工程咨询有限公司注册造价工程师.

2095-3852(2015)05-0645-04

A

TU723.3

10.3963/j.issn.2095-3852.2015.05.026