装备修理目标价格测算的灰色组合预测模型

尚凡葵，安天霞，谢 力，孙胜祥

(1.海军驻青岛造船厂 军事代表室，山东 青岛 266000；2.海军青岛航保修理厂，山东 青岛 266000 ；3.海军工程大学 装备经济管理系，湖北 武汉 430033)



装备修理目标价格测算的灰色组合预测模型

尚凡葵1，安天霞2，谢 力3，孙胜祥3

(1.海军驻青岛造船厂 军事代表室，山东 青岛 266000；2.海军青岛航保修理厂，山东 青岛 266000 ；3.海军工程大学 装备经济管理系，湖北 武汉 430033)

针对装备修理目标价格测算中的小样本和振荡特性，以灰色预测模型及各种相关改进模型为单项预测模型，综合考虑直接应用灰色关联度难以保证组合预测的无偏性和灰色关联度计算的准确性，以及基于灰色绝对关联度的最优组合预测模型在单项预测模型数量多于样本数量时无法求解和绝对关联度信息包含不足的问题，建立了基于灰色关联度排序的装备修理目标价格测算的组合预测模型。通过实例分析证明了该方法的可行性和有效性。

装备修理；目标价格；组合预测；GM(1,1)模型；灰色关联度

装备修理价格工作是军品价格工作的重要组成部分，其中目标价格的生成是装备修理价格形成机制中的核心问题[1]，也是装备修理供需双方关注的焦点问题。由于我国装备修理实际发生费用数据长期统计不规范、装备修理部门或工厂的信息封闭等原因，装备修理价格原始数据积累较少[2]，导致装备修理目标价格的测算成为典型的小样本问题。

灰色系统理论主要是针对小样本、贫信息的不确定性系统进行研究的理论，其中GM(1,1)预测模型更是在小样本预测领域得到广泛的应用[3]，是装备修理价格测算的典型方法之一。由于装备修理故障的随机性，同型装备同级别修理的广度和深度往往会有较大差异，导致装备修理价格具有振荡特征。针对小样本序列的振荡特征，钱吴永等[4]通过加速平移变换将振荡序列变换为单调序列，并通过加权均值生成提高序列的光滑度，进而改善GM(1,1)模型在振荡序列预测中的预测效果；赵宇哲等[5]在文献[4]的基础上，研究了将加权均值生成变换调整为几何平均变换的改进GM(1, 1)模型；崔立志等[6]在文献[5]的基础上，进一步研究了将加速平移变换调整为加速指数变换的改进GM(1,1)模型；杨芬等[7]在文献[5]的基础上，将GM(1,1)模型调整为DGM(1,1)模型；曾波等[8]提出了一种一阶平滑性算子，用于压缩随机振荡序列振幅以提高序列的光滑度，从而改进DGM(1, 1)模型的预测效果。尽管上述灰色预测模型的各种改进形式可以在一定程度上提高装备修理目标价格的测算效果，但究竟哪一种灰色预测模型能够更好地反映装备修理价格的变化规律目前尚无定论。事实上，由于装备故障的不确定性及装备修理价格影响因素多的特点，单一预测模型往往难以准确描述其变化规律[9]。组合预测方法通过综合考虑各单项预测方法的特点，将不同单项预测方法进行组合，使最终预测结果能够充分利用从各单项预测方法中获得的信息，在一定程度上改善预测的效果[10-11]。笔者拟结合装备修理价格测算的特征，以GM(1,1)模型及其各种改进模型为基础，建立装备修理目标价格测算的灰色组合预测模型，以期提高目标价格测算的准确性和稳定性。

1 灰色预测相关定义与模型

1.1 相关定义

定义1 设系统行为数据序列为X=(x(1),x(2),…,x(n)),存在以下3种情况：

(1)∀k=2,3,…,n,x(k)-x(k-1)>0，称X为单调增长序列。

(2)∀k=2,3,…,n,x(k)-x(k-1)<0，称X为单调衰减序列。

(3)若存在k,k′∈{2,3,…,n}，有x(k)-x(k-1)>0，x(k′)-x(k′-1)<0,则称X为振荡序列。令M=max{x(k)|k=1,2,…,n}，m=min{x(k)|k=1,2,…,n}，称T=M-m为振荡序列X的振幅，并记R=M/m。

定义2 设系统行为数据序列为X=(x(1),x(2),…,x(n))，则称变换x(k)d1=x(k)+(k-1)T,k=1,2,…,n，为加速平移变换，记作D1。

定义3 设系统行为数据序列为X=(x(1),x(2),…,x(n))，则称变换x(k)d2=x(k)Rk-1,k=1,2,…,n，为加速指数变换，记作D2。

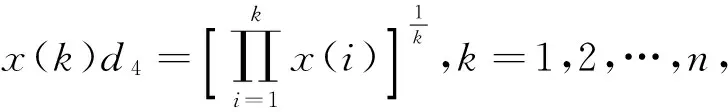
定义6 设系统行为数据序列为X=(x(1),x(2),…,x(n))，则称变换x(k)d5=[(x(k)+T)+(x(k+1)+T)]/4,k=1,2,…,n-1,为序列X的一阶平滑算子，或称一阶平滑性变换，记作D5。

1.2 基本预测模型

1.2.1 GM(1,1)模型

GM(1,1)模型主要是利用原始数列X(0)进行一阶累加生成，然后对生成的序列X(1)建立如下的白化形式方程：

(1)

对式(1)进行求解，得到：

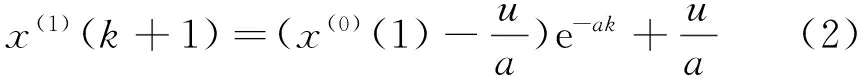
将得到的生成序列的预测值进行一阶累减生成，就得到了原始数据预测值。

1.2.2 DGM(1, 1)模型

设原始数据序列X(0)进行一阶累加生成后的序列为X(1)，则：

x(1)(k+1)=β1x(1)(k)+β2

(3)

式(3)为GM(1,1)模型的离散形式(discretegreymodel,DGM)，称为DGM(1,1)模型。

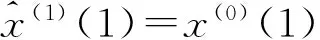
(4)

2 灰色组合预测模型

目前关于灰色组合预测模型的相关研究还处于起步阶段，一般简单地将GM(1,1)模型与其他预测模型进行组合[12-13]，也有少数文献开始探讨基于灰色关联度的组合预测模型[14-15]。

2.1 基于灰色关联度的组合预测模型

设某装备历史修理价格的实际值为y0(k)(k=1,2,…,n)，对该装备修理价格共有m种可行的灰色预测方法，第i种灰色预测方法在第k时刻的预测值为yi(k)(i=1,2,…,m)，在线性组合预测中，组合预测模型一般可以表示为：

yc(k)=w1y1(k)+w2y2(k)+…+wmym(k)

(5)

式中：yc表示组合预测；w1+w2+…+wm=1，为相应单项预测方法的权系数。

定义7 设参考数列为y0(k)，比较数列为yi(k)(k=1,2,…,n)，则令：

(6)

式中：ξi(k)为y0(k)与yi(k)在第k点的关联系数；ρ为待分辨系数，一般取ρ=0.5。

综合各点的关联系数，可以得到y0(k)与yi(k)的关联度ri为：

(7)

文献[14]将y0(k)与yi(k)标准化后，将求得的关联度ri直接作为组合预测的权重，即取wi=ri。

定义8 设参考数列为y0(k)，比较数列为yi(k) (k=1,2,…,n)，则令：

(8)

式中：ε0i表示y0(k)与yi(k)的灰色绝对关联度；Δy0(k)=y0(k)-y0(k-1)；Δyi(k)=yi(k)-yi(k-1)。

文献[15]以组合预测与原始数列的灰色绝对关联度最大为目标函数，建立了组合预测最优模型。

2.2 基于灰色关联度排序的组合预测模型

文献[15]中的灰色组合预测模型存在两点不足之处：①在小样本预测中，当用于组合预测的单项模型的数量多于样本数量时，最优组合预测模型可能无法求解[16]；②式(8)中灰色绝对关联度仅考虑了y0(k)与yi(k)两个序列之间的关系，而式(6)中灰色关联度的计算因考虑了所有待比较的数列之间的整体关系而包含较多信息。针对这两个问题，笔者认为在装备修理目标价格测算的过程中采用文献[14]中的灰色组合预测模型(以定义7中的灰色关联度为基础计算权重)可能更加合适。但是文献[14]中的灰色组合预测模型也存在两点不足之处：①通过对数列标准化后，难以保证所有预测模型产生的序列与原始序列的关联度的和为1，这样也就无法保证组合序列的无偏性[17]，从而影响预测的效果；②计算过程相对复杂，计算过程中的数据误差会迅速放大，且ρ的取值也会影响关联度的计算结果，关联度计算的准确性难以保证。

针对上述问题，笔者认为，尽管采用定义7中公式计算的关联度的准确性难以保证，但装备修理价格的实际值与各灰色预测之间灰色关联度的相对大小是可以保证的。因此，可以考虑采用灰色关联度的排序作为组合预测权重的计算基础。

不妨设装备历史修理价格的实际值序列y0(k)与m种灰色预测模型的拟合值yi(k)序列之间的灰色关联度满足：

r1≤r2≤…≤rm

(9)

则基于灰色关联度排序的组合预测模型为：

yc(k)=w1y1(k)+w2y2(k)+…+wmym(k)

(10)

即某灰色预测模型的关联度越大，其排序越靠前，序号越小，序号的倒数越大，相应的组合预测权重也越大，且满足w1+w2+…+wm=1，组合预测为实际值序列的无偏估计。

3 实例分析

根据对某型装备主要承修单位的修理成本的跟踪调研，获得该型装备连续8年某一级别计划修理成本数据，以各修理单位同一年修理成本的平均值作为基础数据，并经过脱密处理得到该型装备修理成本数据。装备修理目标价格的测算，主要是对装备修理成本的预测，然后再考虑合理的目标利润，作为装备修理目标价格制定的基础。因此，笔者直接以装备修理成本数据为基础进行建模分析，选取前6年的数据作为各预测模型的建模样本，后两年的数据作为模型的检验样本以验证模型预测的有效性。

3.1 单项灰色预测模型

从表1可以看出，某型装备修理成本数据样本量小，且为振荡变化。将原始GM(1,1)模型记为y1，根据上述相关定义，针对振荡序列的GM(1,1)相关改进模型主要包括以下几种：

(1)离散GM(1,1)模型，也称DGM(1,1)模型，记为y2。

(2)对振荡序列样本进行单调性变换，包括加速平移变换和加速指数变换，将经过这两种变换后的GM(1,1)模型分别记为y3和y4。

(3)对单调性变换后的样本再进行光滑性变换，包括加权均值生成变换和几何平均变换。相应的GM(1,1)改进模型有：加速平移变换+加权均值生成变换、加速平移变换+几何平均变换、加速指数变换+加权均值生成变换、加速指数变换+几何平均变换，分别记为y5、y6、y7、y8；还包括经过这些变换后再采用DGM(1,1)模型建模，笔者主要采用文献[7]中的模型，记为y9。

(4)对振荡序列直接采用平滑算子进行变换，如文献[8]中的一阶平滑算子变换，再采用DGM(1,1)模型建模，相应的灰色模型记为y10。

上述y1～y10的拟合数据和预测结果如表1所示。

3.2 灰色组合预测

由于该实例中单项预测模型有10项，而用于建模的样本数仅6个，所有基于最优化的组合预测模型无法适用，笔者主要采用以下几种灰色组合预测模型，预测(拟合)结果见表1。

(1)基于灰色关联度的组合预测模型，笔者对关联度进行了归一化处理，再作为组合预测的权重，记为组合1。

(2)基于灰色绝对关联度的组合预测模型，笔者没有采用最优化模型，而是对灰色绝对关联度进行归一化后作为组合预测的权重，记为组合2。

(3)笔者提出的基于灰色关联度排序的组合

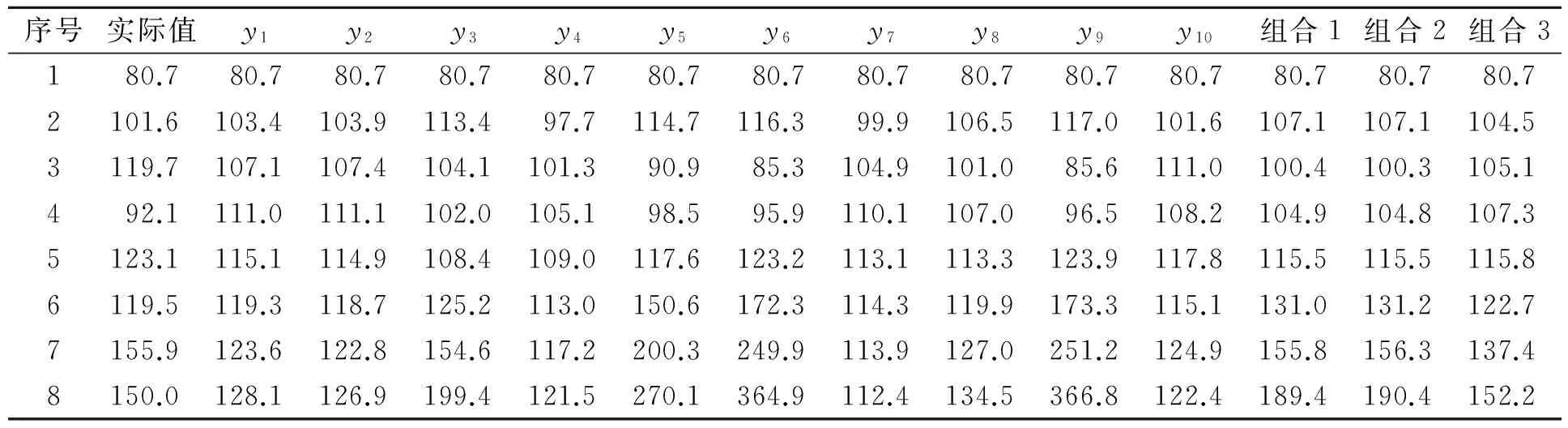
表1 某型装备修理成本实际值与各种预测模型的预测值

预测模型，记为组合3。

3.3 预测结果分析

实例中的10种灰色预测模型和3种灰色组

合预测模型与某装备修理实际成本之间的相对误差的绝对值，以及各预测模型的拟合、预测、整体相对误差绝对值平均见表2。

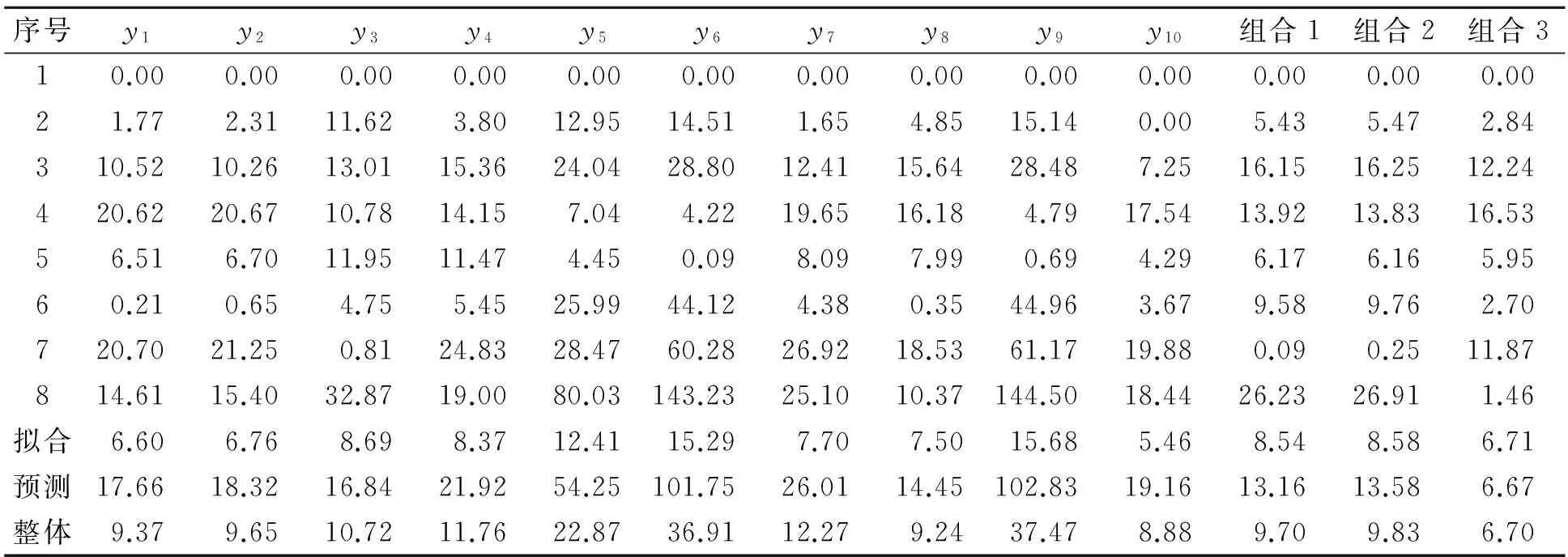
表2 各种预测模型拟合、预测、整体相对误差绝对值平均 %

从表2可以看出，首先，由于灰色系统数列生成的特征及灰色预测建模的特点，各单项预测模型对第1项数据的拟合都与实际值完全相同；其次，由于一阶平滑算子的计算特点，y10对第2项数据的拟合也与实际值相同。

(1)从整体上来看，组合1和组合2的效果差强人意，笔者提出的灰色组合预测模型(组合3)效果最好。因为有4项单项灰色预测模型(y1、y2、y8、y10)的整体效果都优于组合1和组合2。其原因可能是预测误差在灰色(绝对)关联度计算过程中被放大。

(2)从拟合效果来看，3种组合模型并不具备优势，组合1、组合2和组合3在所有模型中分别排在第8位、第9位和第3位。并且y10的拟合效果在所有13种模型中表现最好，其原因之一就是y10对第2项数据的拟合与实际值相同。

(3)从预测效果来看，组合预测的优势则十分明显，3种组合模型的预测效果均优于单一模型，并且笔者提出的基于灰色关联度排序的组合预测模型表现最佳。

4 结论

笔者通过对灰色预测相关定义、GM(1, 1)预测模型、DGM(1,1)预测模型进行阐述，结合装备修理成本样本小且具有振荡型的特点，对灰色预测的各种相关改进模型进行了分析。通过灰色关联分析建立不同装备修理目标价格灰色预测模型的灰色组合预测模型。针对现有灰色组合预测模型中，直接应用灰色关联度产生组合权重，以及通过灰色绝对关联度建立最优组合预测模型时存在的局限性，通过将灰色关联分析获得的各单项灰色预测模型与装备修理成本之间的灰色关联度大小进行排序，根据排序情况建立了基于灰色关联度排序的组合预测模型，并通过对某型装备修理目标价格测算进行了实例分析。总的来说，由于装备故障的不确定性导致了装备修理成本的不确定性，再加上各种主客观因素的影响，造成各单项模型很难准确把握装备修理成本的变化规律，而出现模型拟合效果欠佳的现象。而组合预测能够综合各单项预测模型中所包含的信息，消除单项预测模型中的随机偏差，提高装备修理目标成本预测的稳定性和准确性。

[1] 姜鲁鸣，王伟海，郭召军.推进我军装备价格工作改革的思考[J].军事经济研究，2011(11)：21-24.

[2] 谢力，魏汝祥，陆霞，等.基于强化缓冲算子的装备修理价格预测[J]．武汉理工大学学报(信息与管理工程版)，2010，32(5)：807-810.

[3] 刘思峰，曾波，刘解放，等.GM(1,1)模型的几种基本形式及其适用范围研究[J].系统工程与电子技术，2014，36(3)：501-508.

[4] 钱吴永，党耀国.基于振荡序列的GM(1，l)模型[J].系统工程理论与实践，2009，29(3)：149-154.

[5] 赵宇哲，武春友.灰色振荡序列GM(1，1)模型及在城市用水中的应用[J].运筹与管理，2010，19(5)：155-159.

[6] 崔立志，刘思峰.基于随机振荡序列的GM(1,1)模型性质及其应用[J].数学的实践与认识，2012，42(11)：160-165.

[7] 杨芬，关叶青，曾波，等.基于随机振荡序列的DGM(1,1)模型的建模及应用[J].数学的实践与认识，2013，43(16)：175-180.

[8] 曾波，刘思峰.基于振幅压缩的随机振荡序列预测模型[J].系统工程理论与实践，2012，32(11)：2493-2497.

[9] CANG S, YU H N. A combination selection algorithm on forecasting[J]. European Journal of Operational Research, 2014,234(1):127-139.

[10] 谢力，魏汝祥，尹相平，等.基于改进IOWA组合模型的舰船装备维修费预测[J].系统工程与电子技术，2012，34(6)：1176-1181.

[11] 谢力，魏汝祥，黎利，等.一种小样本双重组合预测模型研究[J]．管理现代化，2014(1)：75-77.

[12] 朱建军，刘思峰，张里，等.基于灰色组合预测的节能政策能源节约量测算模型[J].软科学，2009，23(5)：42-45.

[13] 曾波，刘思峰，方志耕，等.灰色组合预测模型及其应用[J].中国管理科学，2009，17(5)：150-155.

[14] 殷春武.基于灰色关联度的第三产业发展趋势组合预测模型[J].统计与决策，2013(13)：15-18.

[15] 汤少梁，李南，巩在武.灰色绝对关联度组合预测模型的性质研究[J].系统工程与电子技术，2008，30(1)：89-92.

[16] 谢力，魏汝祥，蒋国萍，等.基于分片逆回归的小样本组合预测建模方法[J]．统计与决策，2013(2)：73-76.

[17] 陈华友．组合预测方法有效性理论及其应用[M]．北京：科学出版社，2008：8-75．

SHANG Fankui:Engineer; Naval Representative Room, Quartered at Qingdao Boatyard, Qingdao 266000, China.

[编辑：王志全]

Grey Forecast Combination Model for Estimating Target Price of Equipment Repair

SHANGFankui,ANTianxia,XIELi,SUNShengXiang

Equipment repair price estimation usually has small samples with turbulence characteristics. In the combination model, individual models come from various grey forecast model, and the combination method is based on grey relational analysis. Because the unbiasedness of forecast and the accuracy of grey correlation degree are difficult to meet in the existing grey combination model, and the optimal forecast combination model based on grey absolute correlation degree cannot solve, and the information conceived in grey absolute correlation degree is insufficient, a forecast combination model based on rank of grey correlation degree was proposed. Finally an example was given to verify the availability of this method.

equipment repair; target price; forecast combination; GM(1, 1) model; grey relational grade

2015-03-26.

尚凡葵(1981-)，女，山东东营人，海军驻青岛造船厂军事代表室工程师.

国家社会科学基金资助项目(13GJ003-258，14GJ003-149).

2095-3852(2015)05-0635-05

A

C931

10.3963/j.issn.2095-3852.2015.05.024