绝对重力仪测量有效高度确定
杨 萌 钟 敏 张为民
1 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室,武汉市徐东大街340号,430077
2 中国科学院大学,北京市玉泉路甲19号,100049
绝对重力仪通过测定真空舱中落体自由下落过程中的时间距离对来测定重力值。由于垂直重力梯度的影响,落体下落不同距离处的重力值不相等。落体自由下落20cm,重力值会相应地产生约60μGal的变化[1]。因此,垂直梯度对绝对重力测量结果的影响不可忽视。
顾及垂直重力梯度的影响,采集的时间距离对有两种处理方式。假设垂直重力梯度在下落距离内是常数,将时间距离对组成四阶模型(公式(1)),此时得到的重力值为起始点z=0处的重力值。若垂直重力梯度未知,认为下落过程中重力不受重力梯度的影响,将时间距离对组成二阶模型(公式(2))。此时得到的重力值并不是起始点处的重力值,而是下落到某一点处的重力值,将这一点与z=0处的距离称为有效高度。在重力梯度未知的情况下,精确求解有效高度是重力解算的主要问题。目前,有效高度的计算方法主要有表1列出的几种,但它们都假设初始位置为统一的零点,不符合实际情况。本文推导了一个新的有效高度计算公式,适合于初始位置和初始速度均不为0的情况,并且精度在1μGal以内。

表1 国际绝对重力仪有效高度计算方法Tab.1 Methods for effective measurement height of absolute gravimeter
1 垂直重力梯度对重力的影响
在垂直重力梯度已知的情况下,将绝对重力仪测得的时间距离对按式(1)组成四阶模型:

其中,z0为初始位置,v0为落体下落初始速度,γ为垂直重力梯度值,zi为ti时刻对应的下落距离。通过此模型获得的g0是z=0处的重力值。
在垂直重力梯度未知的情况下,将绝对重力仪测得的时间距离对按式(2)组成二阶模型:
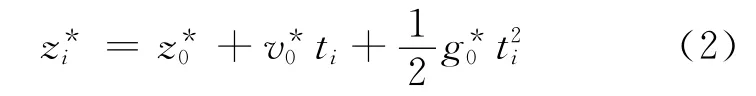
将FG5采集的100次落体分别用两种模型计算重力值,其中每次落体采用100条条纹,相当于12.5cm,重力梯度采用3.086μGal/cm。从图1看出,两种方法计算的重力值相差16~17 μGal。因此,必须按式(3)将改正到z=0处:

其中,Heff为绝对重力仪测量有效高度。

图1 垂直重力梯度变化对绝对重力值的影响Fig.1 The influence of vertical gravity gradient on absolute gravity value
2 绝对重力仪测量有效高度计算
采用最小二乘原理,给出最小二乘条件方程:

在等间距连续测量条件下,上式变成:
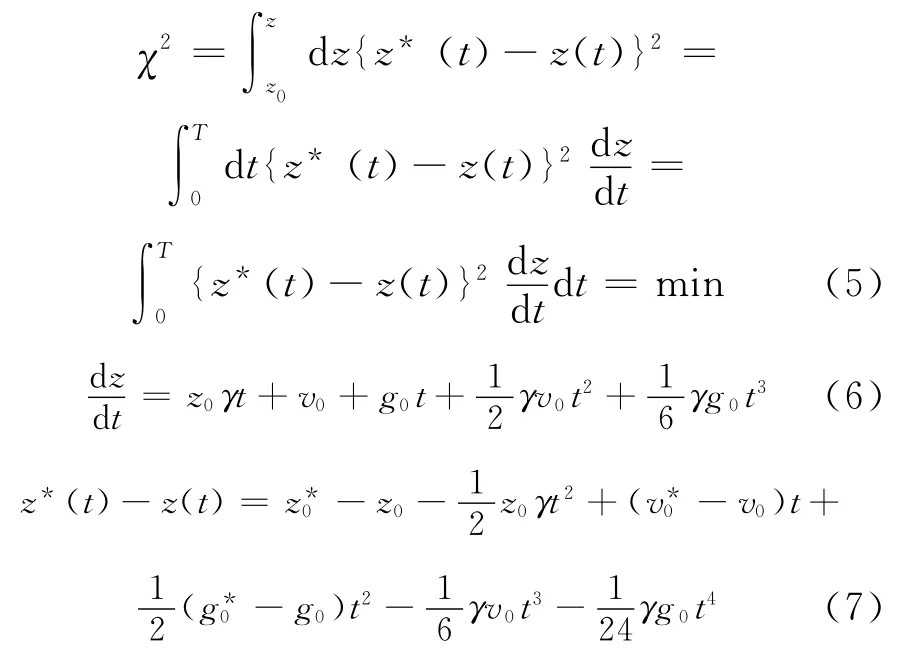
其中,T为落体下落时间。令将(6)、(7)代入式(5),并分别对a0、a1和a2求偏导:

略去高阶项,求得有效高度Heff为:

以上公式中的z0、v0要通过四阶模型求得,但是在重力梯度未知的情况下,只能使用二阶模型。图2、3分别为两种模型计算的初始位置和初始速度值。可以发现,两种模型计算的初始速度和初始位置相等。因此,可以用二阶模型的初始位置、初始速度代替式(9)中的z0、v0,得:


图3 两种模型初始速度对比Fig.3 Initial velocity for two models
利用Zumberge[5]、Niebauer[1]、Timmen[6]以及上述模型得到有效高程,通过式(3)对二阶模型得到的重力值进行有效高程改正。图4为4种模型进行有效高程改正后的重力值与四阶模型得到的重力值偏差,其中,利用式(10)得到的结果偏差大部分都在1μGal以内。图5所示为4种模型计算的RMS,式(10)得到的结果也明显好于其他3种模型。

图4 二阶模型有效高度改正后与四阶模型的差(dif1为Zumberge[5]模型结果;dif2为Niebauer[1]模型结果;dif3为Timmen[6]模型结果;dif4为本文方法的结果)Fig.4 The gravity differences between effective height corrected second-order model and forth-order model(dif1:Zumberge[5] method;dif2:Niebauer[1]method;dif3:Timmen[6]method;dif4:the article method)

图5 RMS值(RMS1为Zumberge[5]模型结果;RMS2为Niebauer[1]模型结果;RMS3 为Timmen[6]模型结果;RMS4为本文方法结果)Fig.5 The RMS for four methods(RMS1:Zumberge[5]method;RMS2:Niebauer[1] method;RMS3:Timmen[6]method;RMS4:the article method)
3 结 语
本文在Niebauer[1]、Murata[4]和Timmen[6]方法基础上,考虑了初始位置和初始速度对重力值测量的影响,更加适用于实际情况。公式相对简洁,且得到的结果明显优于其他3种模型。
致谢:感谢测地所叶文蔚老师的指导。
[1]Niebauer T M.The Effective Measurement Height of Free-Fall Absolute Gravimeters[J].Metrologia,1989,26(2):115-118
[2]Cannizzo L,Cerutti G,Marson I.Absolute-Gravity Measurements in Europe[J].Il Nuovo Cimento C,1978,1(1):39-85
[3]Cook A H.The Absolute Determination of the Acceleration Due to Gravity[J].Metrologia,1965,1(3):84-113
[4]Murata I.A Transportable Apparatus for Absolute Measurement of Gravity[J].Bull Earthquake Res Inst,1978,53:49-130
[5]Zumberge M A,Rinker R L,Faller J E.A Portable Apparatus for Absolute Measurements of the Earth’s Gravity[J].Metrologia,1982,18(3):145-152
[6]Timmen L.Precise Definition of the Effective Measurement Height of Free-Fall Absolute Gravimeters[J].Metrologia,2003,40(2):62-65

