Maneuvering target tracking algorithm based on cubature Kalman filter with observation iterated update*

Hu Zhentao (胡振涛), Fu Chunling, Cao Zhiwei, Li Congcong

(*Instituteof Image Processing and Pattern Recognition, Henan University, Kaifeng 475004, P.R.China)(**School of Physics and Electronics, Henan University, Kaifeng 475004, P.R.China)



Maneuvering target tracking algorithm based on cubature Kalman filter with observation iterated update*

Hu Zhentao (胡振涛)*, Fu Chunling***, Cao Zhiwei*, Li Congcong*

(*Instituteof Image Processing and Pattern Recognition, Henan University, Kaifeng 475004, P.R.China)(**School of Physics and Electronics, Henan University, Kaifeng 475004, P.R.China)

Reasonable selection and optimization of a filter used in model estimation for a multiple model structure is the key to improve tracking accuracy of maneuvering target. Combining with the cubature Kalman filter with iterated observation update and the interacting multiple model method, a novel interacting multiple model algorithm based on the cubature Kalman filter with observation iterated update is proposed. Firstly, aiming to the structural features of cubature Kalman filter, the cubature Kalman filter with observation iterated update is constructed by the mechanism of iterated observation update. Secondly, the improved cubature Kalman filter is used as the model filter of interacting multiple model, and the stability and reliability of model identification and state estimation are effectively promoted by the optimization of model filtering step. In the simulations, compared with classic improved interacting multiple model algorithms, the theoretical analysis and experimental results show the feasibility and validity of the proposed algorithm.

maneuvering target tracking, nonlinear filtering, cubature Kalman filter(CKF), interacting multiple model(IMM)

0 Introduction

Target tracking is used by subjects that realize a process of state modeling, estimation and tracking about the objects observed by means of various observation and calculation methods. As an emerging technique, target tracking is widely applied to the military, civilian and economic fields[1]. Target tracking is classified to maneuvering target tracking and non-maneuvering target tracking by the type and intensity of motions. In the maneuvering case, owing to the variety and complexity of target motion features, it is difficult to describe precisely the motion state of via the single and stationary models, therefore, the multiple model structure is commonly adopted[2]. Compared with the single-model approach, a set for describing the behavior pattern of the system is selected or designed through the multi-model approach where each model matches with a specific system pattern, and the estimation for system state is the reasonable synthesis of filtering results of parallel running filters[3]. Among various multiple model methods and their improved methods, the interacting multiple model (IMM) algorithm is recognized as an effective approach to handle the system model switch problem, which adopts the modeling soft switch mechanism and effectively keeps the balance between model identification and state estimation precision[4,5]. In the conventional IMM structure, the Kalman filter meeting the criterion of the linear minimum variance estimation is selected as the model filter which is able to obtain high precision for linear Gaussian system. However, the performance of the selected nonlinear filter will directly determine the estimation precision of the system state and computation complexity of the algorithm when the estimated system has strong nonlinear or non-Gaussian feature[6,7].

In recent years, the research in nonlinear filter catches much attention by domestic and international experts and scholars in related fields, and some phasic achievements are made. Considering the superiority of Kalman filter in realizing recursive Bayesian estimation, combining with local linearization techniques, the extended Kalman filter (EKF) is constructed under the framework of KF[8,9]. Its basic idea is to linearize the nonlinear systems by taking the advantage of the Taylor series, but this linearization error is large, and it is difficult to get the Jacobian matrix from nonlinear function in many practical problems. To solve such problems, some new nonlinear filtering methods have been proposed combining with the UT transform or numerical differencing technique, such as Unscented Kalman filter (UKF)[10,11], central difference filter (CDF)[12], Ensemble Kalman filter (EKF)[13,14], etc. However, these methods can hardly meet the engineering demands because they lead to sharp decline of estimation accuracy or even filter divergence when handling strong nonlinear and non-Gaussian problems. With the rapid improvement in computer performance, combining with sequential Monte-Carlo simulation method and recursive Bayesian thought, Gordon et al. proposed the particle filter (PF) which consists of two basic steps of prediction and update. Unlike Kalman filter, the prediction step combines a priori model information with sequential Monte-Carlo simulation technique (SMC), and the update step is completed through re-sampling technique. PF can achieve a better filtering accuracy than the EKF and UKF, also it is suitable for the nonlinear systems with arbitrary noise distribution[15]. However, the implementation mechanism sequential of importance sampling and re-sampling makes PF cannot effectively overcome the problems of particle degeneracy and re-sampling particle diversity impoverishment. Moreover, the filtering precision of PF is closely related with the number of system dimension and the amount of particles which limits the universality of its parameters for application objects[16]. In addition, based on the third cubature rule, Arasaratnam et al, proposed the cubature Kalman filter (CKF)[17]. CKF approximates the weighted Gaussian integration by numerical integration, which takes the advantage of high efficiency of calculating the multi-dimensional function integration by using cubature integration numerical value. With 2nequalweightedcubaturepoints(nisthenumberofsystemstatedimension),CubatureKalmanfilteringisprovedthatitsprobabilitydistributionprecisionisbetterthanUKF’safterapproximatingnonlineartransformation.

Based on the above analysis, in the framework of CKF, combining with the mechanism of observation iterated update, a novel improved cubature Kalman filter (ICKF) is constructed to improve the estimation precision of CKF. Then applying ICKF into the algorithm framework of IMM, that is, ICKF is used as the model filter to improve the performance of IMM. On the basis of that, this paper proposes a novel maneuvering target tracking algorithm based on cubature Kalman filter with observation iterated update (IMM-ICKF). The simulations have verified the superiority of the algorithm.

1 Cubature Kalman filter with observation iterated update

1.1 Cubature Kalman filter

The key idea of CKF is to calculate the normal weighted Gaussian integration of functionf(x) by the third cubature integration rule[18], that is

(1)

whereN(x;μ,P) denotes that the random variablexis subject to the normal distribution with meanμand covariance matrixP.L=2ndenotesthenumberofcubaturepoints,andξirepresentstheith cubature point.

(2)

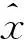
Pk-1/k-1=Sk-1/k-1(Sk-1/k-1)Τ

(3)

Then the estimation for cubature points in the mechanism of state one-step prediction is achieved bySk-1/k-1.

(4)

The diffusion of cubature points in the mechanism of state one-step prediction is realized by the state transform equation.

(5)

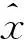
(6)

Then the prediction error covariance matrixPk/k-1is calculated.

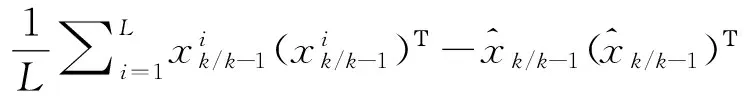
(7)

Pk/k-1=Sk/k-1(Sk/k-1)Τ

(8)

Next, according toSk/k-1, the estimation of cubature point in the mechanism of observation update is realized.

(9)

The diffusion of cubature points in the mechanism of observation update is achieved by observation equation.

(10)

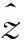
(11)

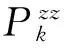
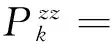
(12)

(13)

(14)

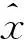
(15)

(16)

1.2 The observation iterated update strategy

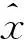
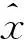
Pk-1/k-1,J=Sk-1/k-1,J(Sk-1/k-1,J)Τ

(17)

(18)

(19)

(20)

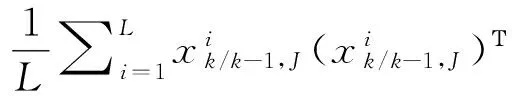
(21)

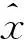
Pk/k,j-1=Sk/k,j-1(Sk/k,j-1)Τ

(22)

(23)

(24)

(25)

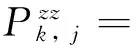
(26)

(27)

(28)

(29)

(30)

The repeating utilization of observation iterated update for improving the estimation performance is limited, and in the practical applications, in view of the balance between the filtering precision and the computation complexity, the number of iterations should not be too large, andJisusually1or2.

2 ManeuveringtargettrackingalgorithmbasedoniteratedcubatureKalmanfilterwithobservationiteratedupdate

2.1 Interacting multiple model

Consider the following multi-model nonlinear system with model switching.

xk=f(xk-1,rk,uk-1)

(31)

zk=h(xk,rk,vk)

(32)

rk～p(rk|rk-1)

(33)

xkandzkdenotethesystemstatevariableandobservation,respectively.ukandvkdenotethesystemprocessnoiseandtheobservationnoisewiththeindependentandidenticaldistributioncharacteristic,respectively.rkdenotesthesystemmodelstate,andD{1,2,…,d}isdefinedasthesetoffirstorderMarkovchainmodelstatesatisfyingthediscretetime,homogeneousandlimitedstate.=Pr{r0=a}denotestheinitialprobabilityofthemodel,andtheprioritransformprobabilityofmodelstateisπab=Pr{rk+1=b|rk=a}.Π=[π1,π2,…,πd]Τdenotes the model transform probability matrix, whereπa=[πa1,πa2,…,πad], andπab=1, anda,b,d∈D.ThebasicprincipleofIMMliesonkeepingallthemodelsinsystemparallelrunningandtheestimationsynthesisofeachmodelfilteringresultsthroughcalculatingtheirmodelprobabilityweight.IMMconsistsoffourpartswhichincludeinputinteraction,modelfiltering,modelprobabilityupdateandoutputinteraction.Thepartofinputinteractioncalculatesthepredictionprobabilityofeachmodel,themodelmixtureprobability,themodelmixturestateestimationofeachmodeland the mixture state estimation error covariance. The part of model filtering implements the filtering process on each model, the state estimationof each model, the state estimation error covariance matrixand the partial error covariance matrixare obtained in this part. Using, the model probability update part calculates each model likelihoodand model probabilityof each model from the model set at timek.Accordingto,andobtained through the above three parts, the output interaction part realizes the calculation of system state estimationk/kand the state estimation error covariance matrixPk/k.

2.2 Interacting multiple model based on cubature Kalman filter with observation iterated update

In the practical application of IMM, the improvement of filtering precision lies on the reasonable selection of sub-filter according to the feature and performance requirements of estimated system. Considering that ICKF has high estimation precision and universality, ICKF is selected as sub-filter in the filtering part of the IMM framework and it promotes the overall performance of IMM by improving the state estimation result of each model. On the basis of that, this section proposes the interacted multi-model algorithm based on cubature Kalman filter with observation iterated update (IMM-ICKF). The recursive implementation process of IMM-ICKF is as follows.

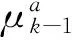
(34)

(35)

(36)

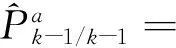
(37)

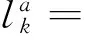
(38)

(39)

(40)

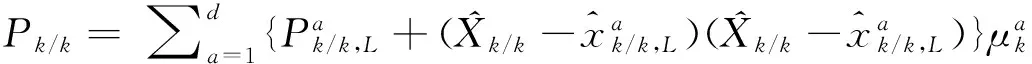
(41)

3 Simulation result and analysis

To verify the feasibility and availability of the proposed algorithm, the observations based on two-coordinate radar are adopted to realize the typical maneuvering target tracking setting in the X-Y plane. The motion of the observed target in Radar scanning area is as follows: uniform circular motion with the turning angular velocity +0.4rad/s2in the first 10 sampling periods; uniform circular motion with the turning angular velocity -0.2rad/s2in 11th to 25th sampling periods; uniform circular motion with the turning angular velocity -0.4rad/s2in the following 10 sampling periods, where plus sign and minus sign denote the different uniform turning directions and plus sign represent the clockwise direction and minus sign counterclockwise. Combining with dynamic characteristics of maneuvering target motion and physical properties of Radar sensors, maneuvering target tracking system state equation and the observation equation are as follows.

θk=tan-1(yk/xk)

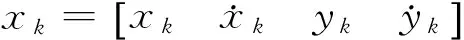
Fig.1showstherealmotiontrajectoryandtheobservationinformationofthetargetinthesimulatedexperimentalsettings.Withmodelprobabilityasmodelidentificationreliabilityindex,Fig.2toFig.6givethemodelutilizationsrespectivelyofthefilteringimplementationofIMM-EKF,IMM-UKF,IMM-CKF,IMM-PFandIMM-ICKF.Fig.7andFig.8showthecomparisonofrootmeansquareerror(RMSE)ofstateestimationofthesefivealgorithmsin50independentexperiments.FromthemodelidentificationeffectivenessofthesefivealgorithmsgivenbyFig.2toFig.6,IMM-EKFisclearlyshowntohavethepooreststabilityoftheaccuracy,theessentialreasonofwhichisthatIMM-EKFcannotprovidestateestimationresultwithhighprecision.Next,IMM-UKFissuperiortoIMM-EKF,whileIMM-PFandIMM-CKFaresuperiortoIMM-UKFtoacertaindegree,butthedefectwhichthesefouralgorithmsmentionedabovehaveincommonisthatthereislargefluctuationofmodelidentificationinthefilteringimplementingprocess.Comparedwiththeotherfouralgorithms,IMM-ICKFimprovestheaccuracyandstabilityofmodelidentificationobviously.Asisknowntoall,intheIMMframework,thesub-filterwithhighprecisionwillsupportIMMtoachievetheeffectiveidentificationofstateevolutionmodelatthecurrenttime,andtheaccuratemodelidentificationwillsupportinturnsub-filtertoobtainnicestateestimationresultinthenexttimefiltering,andthefeatureisreflectedinFig.7andFig.8.Regardingtothefilteringprecisionofalgorithms,accordingtothestateestimationprecision,therankingfromthebesttoworstofallthefivealgorithmsisasfollows:IMM-ICKF,IMM-PF,IMM-CKF,IMM-UKFandIMM-EKF.ItisworthynotingthatthefilteringprecisionofIMM-PFandIMM-CKFissimilar,andIMM-ICKFisbetterthanIMM-CKF,thefundamentalreasonofwhichisthatICKFrealizesimprovementoffilteringestimationprecisionbyintroducingobservationiteratedupdatestrategy.Toquantitativelyanalyzethefilteringprecisionandreal-timeperformanceofthesefivealgorithms,theirmeansofRMSEandaveragerunningtimeiscomparedin50independentsimulationsshowninTable1,andthedataofmeansofRMSEdescribingalgorithmfilteringprecisioninthetableverifiestheresultsanalyzedabove.Inaddition,inthesamesimulationcondition,regardingthetimeconsumedofthesealgorithms,IMM-PFtakethefirstplace,and IMM-ICKF comes to the second but with the highest precision. The above results are conducive to reasonable selection of filters in practical engineering applications.

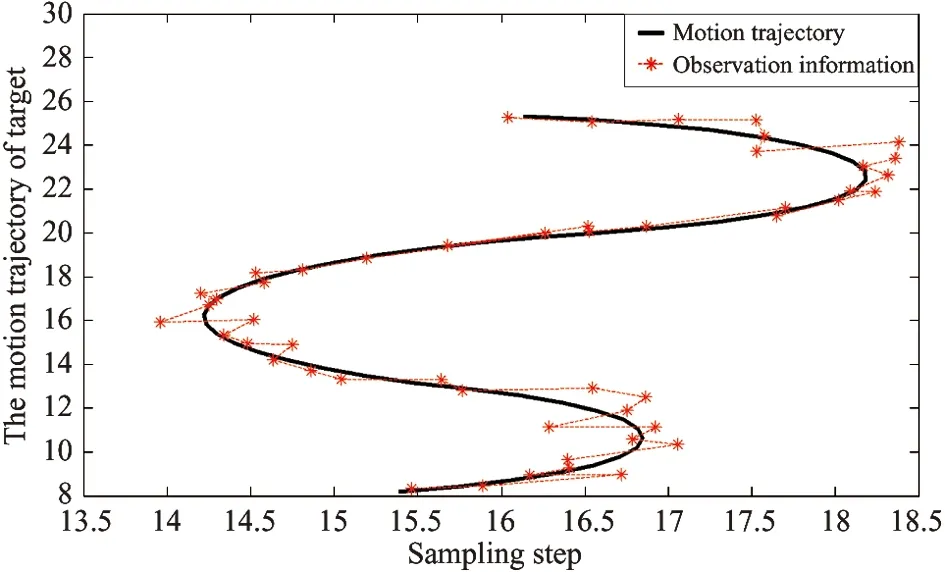
Fig.1 The target trajectory and observation

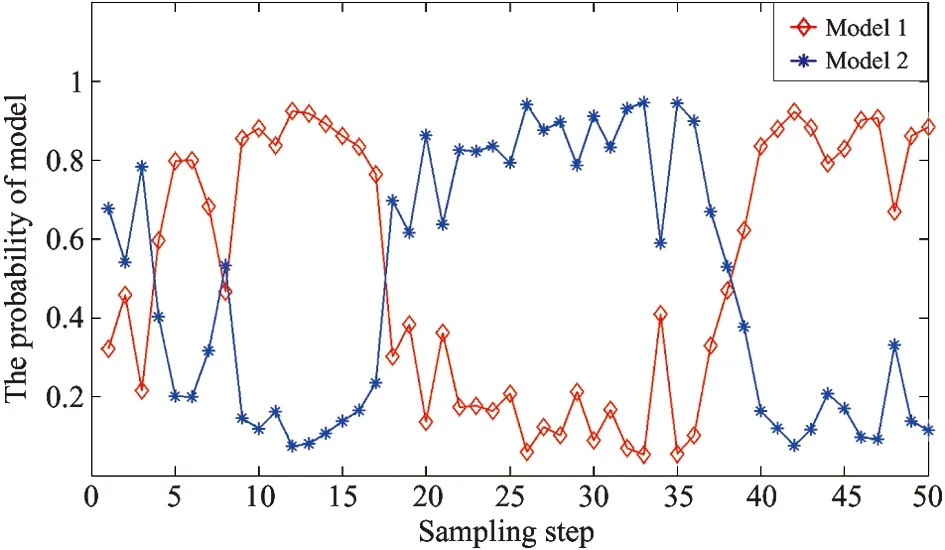
Fig.2 Model probability in IMM-EKF

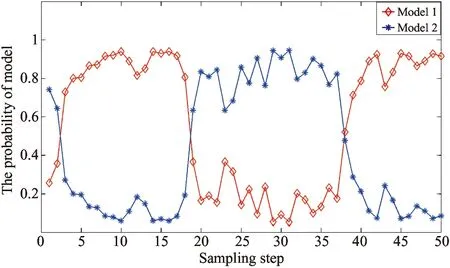
Fig.3 Model probability in IMM-UKF

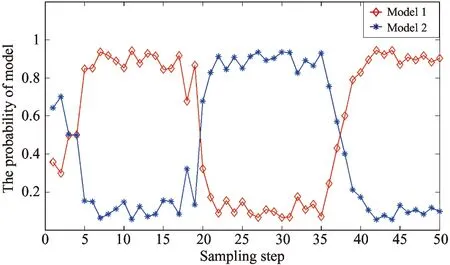
Fig.4 Model probability in IMM-CKF

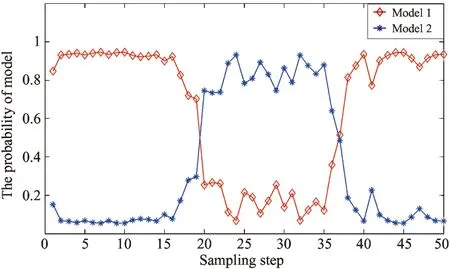
Fig.5 Model probability in IMM-PF

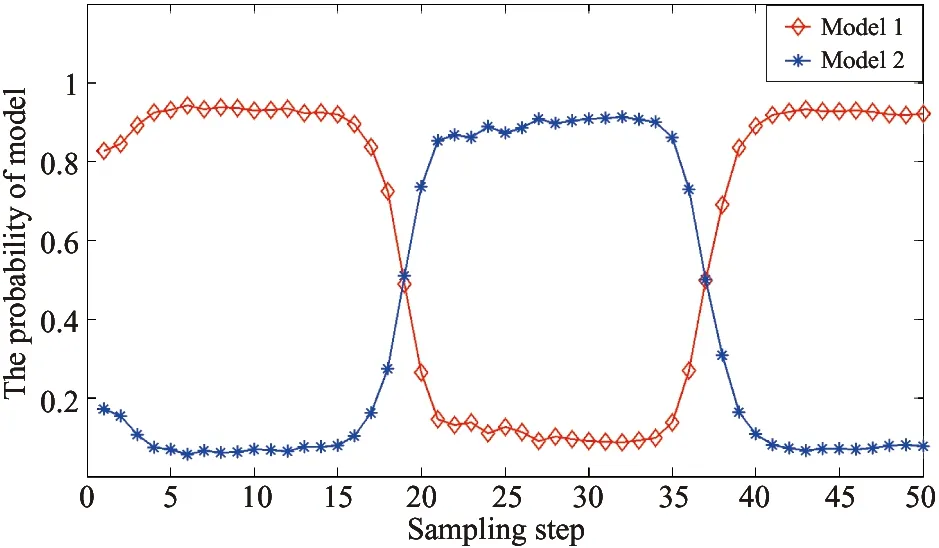
Fig.6 Model probability in IMM-ICKF

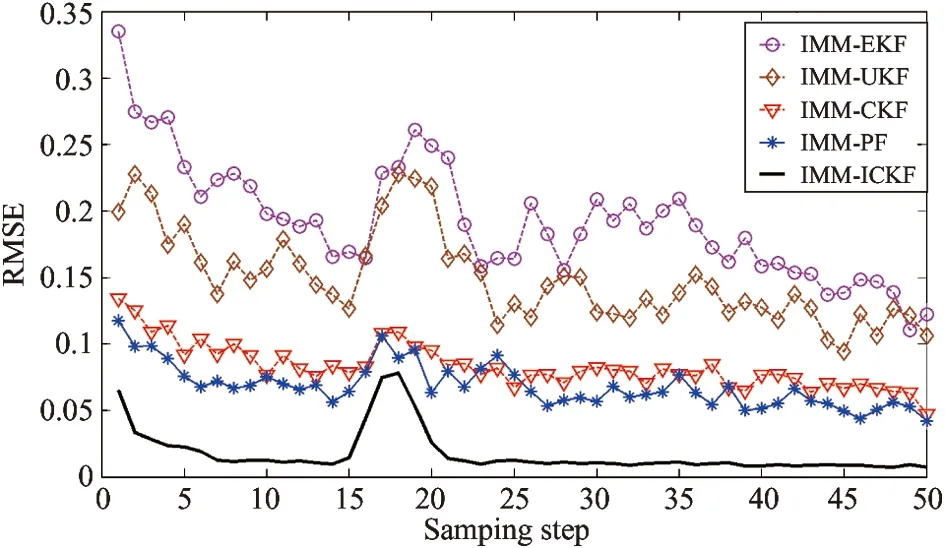
Fig.7 Horizontal direction

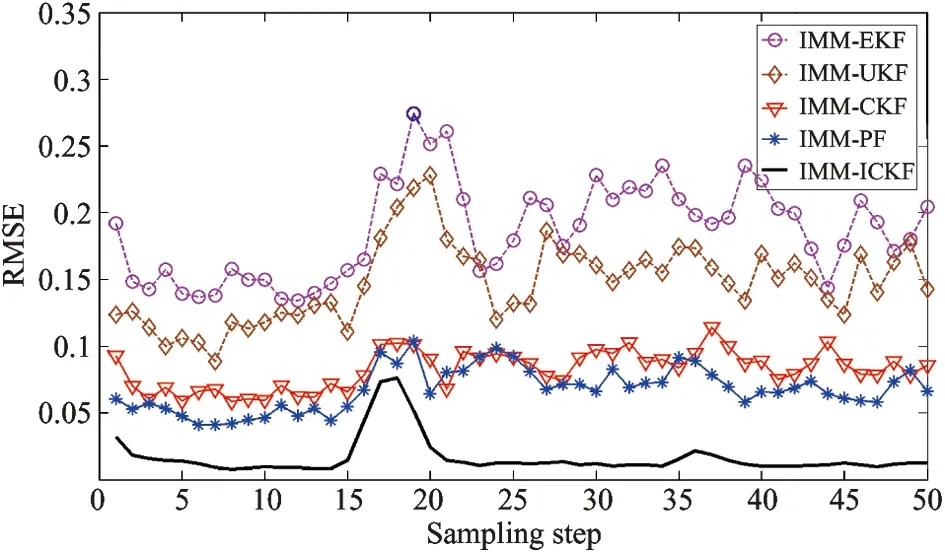
Fig.8 Vertical direction

Table1 The comparison for the mean of RMSE and the average time over 50 independent runs

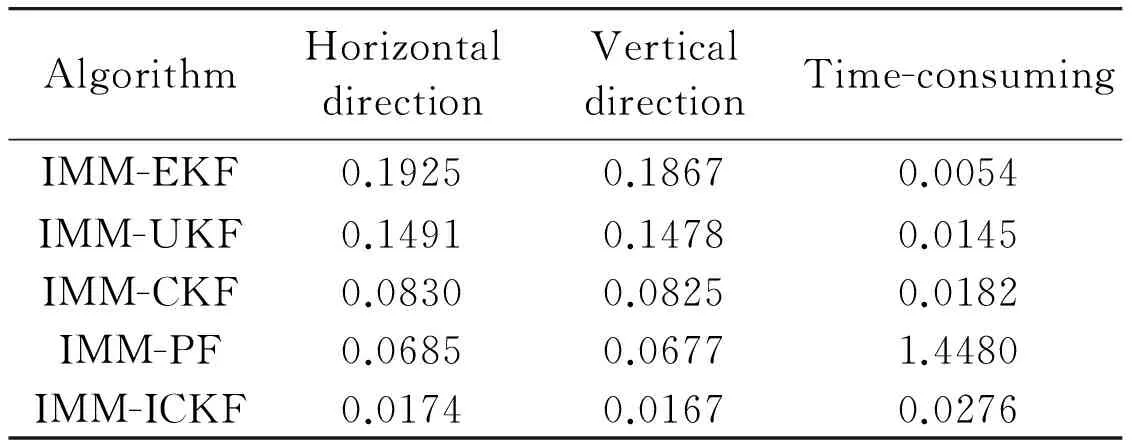
AlgorithmHorizontaldirectionVerticaldirectionTime-consumingIMM-EKF0.19250.18670.0054IMM-UKF0.14910.14780.0145IMM-CKF0.08300.08250.0182IMM-PF0.06850.06771.4480IMM-ICKF0.01740.01670.0276

4 Conclusions

Maneuvering target tracking is always the hot spot and difficulty of researches in target tracking field, this paper gives a maneuvering target tracking algorithm based on CKF with observation iterated update. CKF presented in recent years is an efficient handling method to solve the problem of nonlinear system estimation. In the framework of CKF, the CKF with observation iterated update is proposed by introducing the observation iterated update process. By synthesizing the results of multiple parallel running filters which match the system model, IMM can deal with the problems of uncertainty and variation of system structure and parameters. The novel algorithm realizes the effective identification and estimation of pattern and state by means of dynamically combining ICKF and IMM. Results from practical simulation examples have verified that the proposed algorithm with these effective measures is superior to the existing IMM and its improved algorithms.

[1] Ronald P S Mahler. Statistical Multisource-multitarget Information Fusion. Boston,London: Artech House Publishers,2007

[2] Li W L, Jia Y M. Consensus-based distributed multiple model UKF for jump Markov nonlinear systems.IEEETransactionsonAutomaticControl, 2012,57(1):227- 233.

[3] Jian L, Li X R, Jilkov V P, et al. Second-order Markov Chain based multiple-model algorithm for maneuvering target tracking.IEEETransactionsonAerospaceandElectronicSystems,2013,49(1): 3-19

[4] Nadarajah N, Tharmarasa R, McDonald M, et al. IMM forward filtering and backward smoothing for maneuvering target tracking.IEEETransactionsonAerospaceandElectronicSystems,2012,48(3):2673- 2678

[5] Hammes U, Zoubir A M. Robust MT tracking based on M-Estimation and interacting multiple model algorithm.IEEETransactionsonSignalProcessing, 2011,59(7):3398-3409

[6] Bilik I, Tabrikian J. Maneuvering target tracking in the presence of glint using the nonlinear Gaussian mixture Kalman filter.IEEETransactionsonAerospaceandElectronicSystems, 2010, 46(1): 246-262

[7] Foo P H, Ng G W. Combining the interacting multiple model method with particle filters for maneuvering target tracking.IETRadar,Sonar&Navigation, 2011, 5(3):234 -255

[8] Kai X, Wei C L, Liu L D. Robust extended Kalman filtering for nonlinear systems with stochastic uncertainties.IEEETransactionsonSystems,ManandCybernetics,PartA:SystemsandHumans, 2010, 40(2): 399-405

[9] Gustafsson F, Hendeby G. Some relations between extended and unscented Kalman filters.IEEETransactionsonSignalProcessing, 2012, 60(2):545-555

[10] Dunik J, Simandl M, Straka O. Unscented Kalman filter: aspects and adaptive setting of scaling parameter.IEEETransactionsonAutomaticControl, 2012,57(9): 2411-2416

[11] Dini D H, Mandic D P, Julier S J. A widely linear complex unscented Kalman filter.IEEESignalProcessingLetters, 2011,18(11):623 -626

[12] Wang Y F, Sun F C, Zhang Y A, et al. Central difference particle filter applied to transfer alignment for SINS on missiles.IEEETransactionsonAerospaceandElectronicSystems, 2012, 48(1):375- 387

[13] Evensen G. Sequential data assimilation with a nonlinear quasigeostrophic model using Monte Carlo methods to forecast error statistics.Geophys,1994, 99(5):143-162.

[14] Evensen G. The ensemble Kalman filter for combined state and parameter estimation.IEEEControlSystems, 2009, 29(3): 83-104

[15] Karlsson R. Particle filter for positioning and tracking applications[D dessertation]. Linkoping: PhD thesis of Linkoping University, 2005

[16] Cappe O, Godsill S J, Moulines E. An overview of existing methods and recent advances in sequential Monte Carlo.ProceedingsoftheIEEE, 2007,95(5):899-924

[17] Arasaratnam I, Haykin S. Cubature Kalman filters.IEEETransactionsonAerospaceandElectronicSystems, 2009, 54(6):1254-1269

[18] Arasaratnam I, Haykin S, Hurd T R. Cubature Kalman filtering for continuous discrete systems: theory and simulations.IEEETransactionsonSignalProcessing, 2010,58(10): 4977-4993

Hu Zhentao, born in 1979. He received his Ph.D degrees in Control Science and Engineering from Northwestern Polytechnical University in 2010. He also received his B.S. and M.S. degrees from Henan University in 2003 and 2006 respectively. Now, he is an assistant professor of college of computer and information engineering, Henan University. His research interests include complex system modeling and estimation, target tracking and particle filter, etc.

10.3772/j.issn.1006-6748.2015.01.006

*Supported by the National Nature Science Foundations of China (No. 61300214, U1204611, 61170243), the Science and Technology Innovation Team Support Plan of Education Department of Henan Province (No.13IRTSTHN021), the Science and Technology Research Key Project of Education Department of Henan Province (No.13A413066), the Basic and Frontier Technology Research Plan of Henan Province (No.132300410148), the Funding Scheme of Young Key Teacher of Henan Province Universities, and the Key Project of Teaching Reform Research of Henan University (No.HDXJJG2013-07).

*To whom correspondence should be addressed. E-mail: fuchunling@henu.edu.cnReceived on Oct. 25， 2013