Filtered-beam-search-based approach for operating theatre scheduling*

Zhou Binghai (周炳海), Yin Meng

(School of Mechanical Engineering, Tongji University, Shanghai 201804, P.R.China)



Filtered-beam-search-based approach for operating theatre scheduling*

Zhou Binghai (周炳海)*, Yin Meng

(School of Mechanical Engineering, Tongji University, Shanghai 201804, P.R.China)

To improve the efficiency of operating rooms, reduce the hospital’s costs and improve the level of service qualities, a scheduling method is presented based on a filtered-beam-search-based algorithm. Firstly, a scheduling problem domain is described. Mathematical programming models are also set up with an objective function of minimizing related costs of the system. On the basis of the descriptions mentioned above, a solving policy of generating feasible scheduling solutions is established. Combining with the specific constraints of operation theatres, a filtered-beam-search-based algorithm is put forward to solve scheduling problems. Finally, simulation experiments are designed. The performance of the proposed algorithm is evaluated and compared with that of other approaches through simulations. Results indicate that the proposed algorithm can reduce costs, and are of practicality and effectiveness.

operating theatres, scheduling, algorithm, filtered beam search, costs

0 Introduction

In response to multiple challenges, hospitals have undergone the increasing pressure of providing high quality surgeries while minimizing operational related costs. An effective and efficient scheduling system of operating rooms provides an appealing solution to the challenging problem[1].

Scheduling problems of operating theatres were studied in last decades. Ref.[1] presented a simple heuristic scheduling algorithm. Ref.[2] addressed a problem which considered assigning operations to the time slots available in a planning horizon. Ref.[3] modeled a multi-period, multi-resource, patient-priority-based surgical case for scheduling problems as a mixed-integer programming model, and solved it using the first fit descending-based algorithm. Ref.[4] addressed a scheduling problem where patients with different priorities were scheduled for elective surgeries in a surgical facility, which had a limited capacity. Ref.[5] considered the patient’s recovery was allowed in operating rooms, and the problem was modeled as a 4-stage hybrid flow shop problem with blocking constraints, and successfully solved thanks to the Lagrangian relaxation method. Ref.[6] focused on the scheduling problem of the ophthalmology department such that there was no overload on any of the beds, and the problem was solved by P||Cmax algorithm by forecast the surgery time, while in this method only the scheduling problem of time cost was considered. Focusing on the scheduling problem of the cardiothoracic department, Ref.[7] considered patients’ stochastic durations for the stay in the intensive care unit (ICU) and in the medium care unit (MCU), and built a mixed integer linear programming model to determine a cyclic master operation schedule. Ref.[8] focused on generating an optimal surgery schedule of elective-patient in multiple operating theatres, which considered the intra-operative care and recovery phases. A scheduling method of two stages was described in Ref.[9]. The first stage was described as a set-partitioning integer-programming model and was solved by a column-generation-based heuristic procedure. The second stage was treated as a two-stage hybrid flow shop problem and solved by a hybrid genetic algorithm. Ref.[10] presented two-stage approach for planning and scheduling of operating theatres. However, it was possible that the efficiency of the final operating program would be influenced by a bad assignment of surgical cases in the first phase.

At present, most existing methods in literatures do not consider surgeons’ availability in operating rooms and the postoperative period. It cannot fully adapt to the practical applications. Moreover, structural heuristic algorithms are rarely proposed. Here, on the basis of the mentioned literatures, the scheduling problem of operating theaters mentioned above is solved by using a novel filtered beam search approach.

1 Model description and formulations

The scheduling problem of elective surgeries is considered at hospital operating theatres over a finite horizon ofDperiods. The operating theatre is composed of several operating rooms and one or more recovery rooms where several beds will be available for patients to recuperate[11,12]. In order to describe the scheduling problem of operating theatres effectively, some basic assumptions are described as follows: (1) Each patient will get a recovery bed after his or her unique surgical operation in an operating room. (2) All surgical operations can be performed in any available operating rooms. (3) The surgeon for each elective case is determined in advance and cannot be changed. (4) All elective surgeries are hospitalized before surgeries. (5) Each operating room has an identical overtime hours. (6) One surgeon must perform only one surgical operation in the same operating room simultaneously. (7) A surgeon can carry out operations only when he or she is available.

To give a formal description of the scheduling problem, the parameters and variables are defined as follows.

DPlanninghorizonSNumberofoperatingroomsNNumberofelectivecasestnEarliestperiodtoperformelectivecasendnDurationofelectivecasenfcndsCostofperformingelectivecaseninsthoper-atingroomondthdayrcndCostofrecoveringelectivecaseninrecoveryroomondthdayTORRegularoperationtimeTovertimeRegularovertimehourscdsBeyondstandardoperationtimecostinsthoperatingroomondthdaycodsBeyondstandardovertimehourscostinsthoperatingroomondthdayudsUnderutilizationcostinsthoperatingroomondthdayRdNumberofrecoverybedsondthdayxnsd=1Ifelectivecasenisperformedinsthoperatingroomondthday,and0otherwiseys=1Ifsurgeonpwhoperformoperationnisa-vailableinsthoperatingroomondthday,and0otherwiseλnd=1Afteroperation,patientnisassignedtothebthrecoverybed,or0otherwiseωns=1Ifsurgicaloperationnisassignedtooperat-ingrooms,or0otherwise

The scheduling objective is to minimize the sum of the expected operating room utilization costs and the elective-patient-related costs, which is defined as

(1)

where

(2)

Eq.(2)representsthetimethatthetotaloperationtimeofallelectivecasesareassignedtotheoperatingroomsexceedss’s regular capacity on thedthday.

(3)

Eq.(3)indicatesthetimethatthetotaloperationtimeofallelectivecasesassignedtotheoperatingroomsexceedss’s overtime capacity on thedthday.

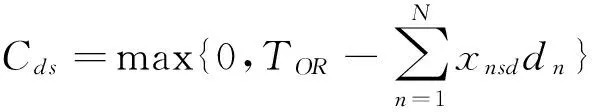
(4)

Eq.(4)showstheidletimeofoperatingroomson thedthday.

Based on assumption Eq.(1), it is a case assignment constraint. An operating room is given no more than one assigned elective case at any time on a given day. The following equation must be satisfied.

(5)

Toensurethetotaloperationtimeofallsurgeriesdoesnotexceedtheoperatingroom’savailablecapacity.Itisatimeconstraintwhichshouldsatisfythefollowingrequirement.

(6)

Itisacapacityconstraint.Toguaranteethenumberofpatientstransferredtotherecoveryroomdoesnotexceedthenumberofavailablerecoverybeds,thefollowinginequalitymustbeobeyed.

(7)

Accordingtoassumption(6)，eachsurgeoncannotperformtwosurgeriesonagivendayatthesametime.Thefollowingrelationmustbefollowed.

tj≥ti+di+M(3-ωis-ωjs-yijs),i≠j,∀s=1,2,…,S

(8)

Thescheduleshouldbefullymadeaccordingtothepracticalapplicationssothatsurgeons'availabilitiescouldbeassured.Thefollowinginequalitymustbeobeyed.

tn+dn-M(1-yds)≤TOR+Tovertime,∀n=1,2,…,N,∀d=1,2,…,D

(9)

Consequently,theschedulingproblemofoperatingtheatresmentionedabovecanbetransformedtoanonlinearprogrammingproblemwithEq.(1)astheobjectivefunctionandEqs(2)～(9)astheconstraints.

2 Proposedschedulingalgorithm

Inthispaper,theschedulingproblemofoperatingtheatresisanalyzedonthebasisoftheoperatingtheatresystemconsideredelectivepatientsastheprimaryresource.Afiltered-beam-search(FBS)-basedalgorithmisdevelopedtosolvetheschedulingproblem.

Filteredbeamsearchisanextensionofbeamsearch.Beamsearchisanadaptationofthebranchandboundmethodinwhichitonlyexploresthepromisingnodeslevelbylevelwithoutbacktracking[13,14].Afilteringmechanismisproposedtodiscardsomenodeswhichdonotsatisfyconstraints,andtoevaluatesomenodeswhichsatisfyconstraints.Generally,asuccessfulFBS-basedalgorithmforaspecificschedulingproblemshouldsolvefourrepresentationfactors: (1)searchtreerepresentationforasolutionspacedefinition; (2)branchingscheme; (3)determinationofbeamwidthandfilterwidth; (4)local/globalevaluationfunctionselection[14,15].

(1)Thesolutionspacecanbevisualizedasasearchtreewitheachpathinthetreerepresentingapotentialsolution[15].Inthetree,eachnodegeneratedbybranchingschemerepresentsaschedulingdecision,involvesindeterminingthestartingtimeoftheelectivecasenin the selected operating room, namelytn.Alinebetweentwonodesrepresentsthedecisionofaddingacasetotheexistingpartialschedule.InafinitehorizonofDperiods, according to the constraints, a complete schedule is composed of nodes and lines between nodes.

(2) The branching scheme is described as follows: letSlbethesetofschedulableoperationsatlevell, ∂*=min(∂s)，where∂sistheearliesttimeofanoperatingroomthatcanperformelectivecases,s∈Sl.Ifk∈Sl∧∂k=∂*,thencasekwill be a node of levell.

(3)The selection of beam width and filter width appears to be very specific[16]. In general, the determination of beam width and filter width has a significant effect on the performance of FBS-based algorithms. Therefore, different combinations of beam width and filter width will be investigated to balance the computational time and the solution quality[14,15].

(4) The selection of evaluation functions will affect the solution quality. Here, dispatching rules are investigated as local and global evaluation functions. Since the local evaluation function is quick but may be poor, while global evaluation function is more accurate but more computationally demanding, and dispatching rules can make a trade-off between them.

On the basis of the descriptions mentioned above, the flow chart of the proposed algorithm is shown in Fig.1.

The procedure steps of the proposed algorithm are described as follows:

Step 1: Initialization. Letbn=0,l=0; determine beam widthb, filter widthf; input planning horizonD，the number of operating roomsS; input the regular operation timeTOR,regularovertimehoursTovertime,thedurationdnoftheelectivecasen, and let the partial schedule setPSbe null.

Step 2: Determine availability. Determine whether a surgeon is available or not. If he or she is available, then go to step 3, otherwise exit the algorithm.

Step 3: According toD，S，TOR，Tovertime，dntodeterminethenumberofelectivecasesT.

Step 4: Determining beam nodes:

Step 4.1: Generate nodes from the root node with the branching scheme. Check the total number of nodesN. Letl=l+1, updatePSwith generated nodes.

Step 4.2: IfN>b, compute the global evaluation function values for all nodes and selectbof cases as initial beam nodes in terms of

(10)

At the same time, determine potential setPS.

Step 4.3: Form a set of candidate scheduling elective cases:ΔT=T-PS.

Step4.4:IfN≤b,movedowntoonemorelevel,letl=l+1, and generate new nodes by branching scheme withPSand updatePS.

Step 5:bn=bn+1

Step 5.1: Ifbn≤b：letl=l+1. Ifl≤T,generatenewnodes(thenumberofnodesisNbn,l)fromthebeamnodeaccordingtothebranchingschemewithPSbnas the partial schedule represented by the beam node. Compute the local evaluation function values of all nodes generated in terms of and select min(Nbn.l,f)ofnodeswiththebestvaluesforfurtherevaluation.Whileifl>T,gotoStep5.3.Ifbn>b, then go to step 6.

Fig.1 The flow chart of the proposed algorithm

(11)

Step 5.2: Calculate the global evaluation function values of min(Nbn.l,f)ofnodesobtainedbyStep5.1.SelectthenodewiththebestvalueandaddthenodeintothepartialschedulesetPSbn,anddeletetheselectednodesfromΔT.GobacktoStep5.1.

Step5.3:Formulatethebnthcomplete schedule setPSbn.

Step6:Generatethefinishingtimeofeachrecoverybedintherecoveryroom,calculateAds,BdsandCds,accordingtotheobjectivefunctionselectschedulesetwiththebestobjectivefunctionvalueamongPSbn.

3 Simulationanalysis

Underthepreconditionofthesameobjectivefunctionandbranchingscheme,thequalityoftheproposedalgorithmisrelatedtobeamwidthband filter widthf. Differentbandfare tested and evaluated.

3.1 Relationship between objective function value andb

During the same condition that the number of operating rooms is equal to 5, the regular operating time is equal to 14 hours, and the overtime is equal to 2 hours, the duration of elective cases is randomly generated from [60,1000]. Setb=1,2,…,10,f=1,2,4,6,8,10,and the local/global evaluation functions are shortest processing time (SPT) rules. The average outcomes of 10 repeated experiments of the proposed algorithm are shown in Fig.1.

Fig.2 shows that average objective function value (AOFV) for each expected valuefhas similar tendency under the variations ofb. Whenbincreases beyond 10, AOFV almost keeps constant. Based on this experiment, it indicates that whenfremains unchanged, asbincreases, andb<10, the proposed algorithm can get better scheduling results.

Fig.2 The relationship between objective values andb

3.2 Relationship between objective function value andf

During the same condition that the number of operating rooms is equal to 5, the regular operating time is equal to 14 hours, and the overtime is equal to 2 hours, the duration of elective cases is randomly generated from [60,1000]. Setf=1,2,…,10,b=1,2,4,6,8,10, and the local/global evaluation functions are SPT rules. The average outcome of 10 repeated experiments of the proposed algorithm is shown in Fig.3. The samples are different from the ones used in Section 3.1.

Fig.3 The relationship between objective values andf

For individualb,Fig.3showsthatAOFVdecreasesfastwiththeincreaseoff. Though the curves of AOFV are not identical, the general variation tendency of all curves is uniform.

Table 1 shows that whenbkeeps unchanged withfincreasing from 1 to 10, the AOFV change rates are always larger than the case thatfstays constant withbchanging. Moreover, comparing Fig.2 to Fig.3, whenbremains unchanged asfincreases, the proposed algorithm can obtain better results than the cases whenfremains unchanged asbincreases. It is noticeable that bothfandbplay an important role in the good performance of the proposed algorithm, andfis more crucial thanb.

Table 1 AOFV change rate

3.3 Comparison with other approaches

To compare the system performance of the proposed algorithm with other algorithms effectively, some variables are defined as follows.

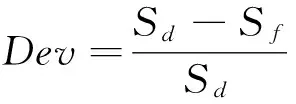
ToinvestigatetheproposedFBSalgorithm(b=2,f=2),itsperformanceiscomparedwithdispatchingrules(firstinfirstserve(FIFS),longestprocessingtime(LPT),weightedduedate(WDD),earliestduedate(EDD)[18,19])underthelengthofthedifferentplanninghorizon,differentelectivecasesanddifferentoperatingrooms.AndtheresultsareshowninTable2.Sincesolutiontimesofthedispatchingrulesareverysmall,theCPUtimeoftherulesisnotincludedinTable2.Asexpected,theperformanceoftheproposedalgorithmintermsofDevis much better than the rules. The averageDevis 55.91%, 42.21%, 55.65%, 59.10% for FIFS, LPT, EDD, WDD, respectively. Even though beam search is a branch and bound based algorithm, the CPU time is not very long. The elective cases increase from 41 to 49, the CPU time rises from 0.002ns to 15000ns. The CPU time is small.

To further investigate the proposed algorithm (b=2,f=2),itsperformanceiscomparedwithGAandPSOalgorithms(thepopulationsize=80,thenumberofiteration=300)underdifferentsizesofelectivecasesanddifferentnumberofoperatingrooms.AndtheresultsareshowninTable3.Becausethereisnoaffectiontotheanalysisofthealgorithmperformanceforthedays,thedaysarenotinvolvedinTable3.Regardlessofsize,thesolutionqualityoftheFBSalgorithmisbetterthantheGAandPSOalgorithms.TheGAandPSOalgorithms’runningtimereportedforeachproblemismuchlargerthantheCPUtimerequirementoftheproposedalgorithm.Therefore,theproposedalgorithmhasbetterperformanceonbothCPUtimeandqualityofsolutions.

4 Conclusions

(1)Theproposedalgorithmcaneffectivelysolvetheschedulingproblemofoperatingtheatreswiththeconsiderationoftheavailabilityofsurgeons.Itcanalsoreducetheexpectedoperatingroomutilizationcostsandtheelective-patients-relatedcostseffectively.

(2)Sincethealgorithmcansolvetheschedulingproblemwithinashortperiodofrunningtime,itcancarry out an on-line scheduling problem of operations.

Table 2 Comparison of simulation results with dispatching rules

Problem*: the number of days*the number of elective cases*the number of operating rooms

Table 3 Comparison of simulation results with improved meta heuristics

Problem**: the number of elective cases*the number of operating rooms

(3) Compared with dispatching rules, GA and PSO algorithms, the results show the proposed algorithm is more competitive.

(4) Not only the proposed algorithm can be used to solve static scheduling problem of operating theatres, but also it can be used to implement real-time scheduling problem of operating theatres in the future.

[1] Su M C, Lai S C, Wang P C, et al. A SOMO-based approach to the operating room scheduling problem.ExpertSystemswithApplications, 2011, 38(12): 15447-15454

[2] Liu Y, Chu C, Wang K. A new heuristic algorithm for the operating room scheduling problem.Computers&IndustrialEngineering, 2011,61(3): 865-871

[3] Bharathwaj V, Pratik J P, Rosalyn S, et al. A dual bin-packing approach to scheduling surgical cases at a publicly-funded hospital.EuropeanJournalofOperationalResearch, 2013, 224(3): 583-591

[4] Min D, Yih Y. An elective surgery scheduling problem considering patient priority.Computers&OperationsResearch, 2010, 37(6): 1091-1099

[5] Augusto V, Xie X, Perdomo V. Operating theatre scheduling with patient recovery in both operating rooms and recovery bed.Computers&IndustrialEngineering, 2010, 58(2): 231-238

[6] Devi S P, Rao K S, Sangeetha S S. Prediction of surgery times and scheduling of operation theaters in ophtholmology department.JournalofMedicalSystems, 2012, 36(1): 415-430

[7] Adan I, Bekkers J, Dellaert N, et al. Patient mix optimisation and stochastic resource requirements: a case study in cardiothoracic surgery planning.HealthCareManagementScience, 2009, 12(2): 129-141

[8] Wang Y, Miao Y, Zhu H, et al. A particle swarm optimization algorithm on the surgery scheduling problem with downstream process. In: Proceedings of the 25th Chinese Control and Decision Conference, Guiyang, China, 2013. 850-855

[9] Fei H, Meskens N, Chu C. A planning and scheduling problem for an operating theatre using an open scheduling strategy.Computers&IndustrialEngineering, 2010, 58 (2): 221-230

[10] Souki M, Rebai A. Heuristics for the operating theatre planning and scheduling.JournalofDecisionSystems, 2010, 19 (2): 225-252

[11] Guerriero F, Guido R. Operational research in the management of the operating theatre: a survey.HealthCareManagementScience, 2011, 14(1):89-114

[12] Lamiri M, Xie X L, Zhang S G. Column generation approach to operating theater planning with elective and emergency patients.IIETransactions, 2008,40(9)：838-852

[13] Wang S J, Xi L F, Zhou B H. Filtered-beam-search-based algorithm for dynamic rescheduling in FMS.RoboticsandComputer-IntegratedManufacturing, 2007, 23(4):457-468

[14] Wang S J, Zhou B H, Xi L F. A filtered-beam-search-based heuristic algorithm for flexible job-shop scheduling problem.InternationalJournalofProductionResearch, 2008, 46(11): 3027-3058

[15] Sabuncuoglu I, Bayiz M. Job shop scheduling with beam search.EuropeanJournalofOperationalResearch, 1999, 118(2): 390-412

[16] Coffin M A, Taylor III B W. R & D project selection and scheduling with a filtered beam search approach.IIETransactions, 1996, 28(2): 167-176

[17] Liu Z X, Wang S M. Research on parallel machines scheduling problem based on particle swarm optimization algorithm.ComputerIntegratedManufacturingSystems, 2006, 12(2):183-296

[18] Armentano V A, Ronconi D P. Tabu search for total tardiness minimization in flowshop scheduling problems.Computers&OperationsResearch, 1999, 26(3): 219-235

[19] Sen T, Suleka J M, Dileepan P. Static scheduling research to minimize weighted and unweighted tardiness: a state-of the-art survey.InternationalJournalofProductionEconomics, 2003, 83(1): 1-12

Zhou Binghai, was born in 1965, He received M.S. and Ph.D degrees respectively from School of Mechanical Engineering, Shanghai Jiaotong University in 1992 and 2001. He is a professor, at Tongji University. He is the author of more than 140 scientific papers. His current research interests are scheduling, modeling, simulation and control for manufacturing systems, integrated manufacturing technology.

10.3772/j.issn.1006-6748.2015.01.001

*Supported by the National Natural Science Foundation of China (No. 61273035, 71471135)

*To whom correspondence should be addressed. E-mail: bhzhou@tongji.edu.cnReceived on Oct. 23， 2013