GPS／BDS单历元基线解算中随机模型的确定

陶庭叶 王志平 蒋俊儒

1 合肥工业大学土木与水利工程学院，合肥市屯溪路193号，230009

单历元基线解算可使GPS／BDS组合系统动态定位发挥更大的优势［1］。在进行单历元基线解算时，若仅用相位观测值，观测方程是秩亏的，故通常会引入伪距观测值进行改善，从而在观测方程中出现不同系统、不同类型的观测值。对于分别来自GPS和BDS的伪距和载波观测值，其精度不同，在平差处理中也应赋予不同的权值。以往的组合系统相对定位中，常用的观测值随机模型有经验模型、基于高度角的随机模型和基于信号强度的随机模型。本文引入验后估计的方法，根据预平差的改正数，重新确定来自不同系统、不同类型观测值的随机模型。

对观测量确定合理的随机模型，可有效降低各种系统残余误差的影响［2］，提高导航定位的精度［3］。本文对实际观测数据进行处理，分析GPS／BDS组合系统单历元基线解算中不同随机模型对基线解的具体影响。

1 GPS／BDS组合系统单历元基线解算

单历元基线解算的关键在于模糊度的准确搜索。在计算中，仅利用相位观测值时观测方程是秩亏的，可以引入伪距观测值来解决。但伪距观测值精度低，方程浮点解的精度不高，导致单历元模糊度搜索难度较大。针对这一问题，本文采用文献［4］中的方法缩小模糊度搜索空间，提高模糊度搜索的稳定性。

1.1 双差宽巷模糊度固定

因为宽巷观测值波长较长，模糊度易确定，可以先结合GPS伪距和两系统的宽巷观测值进行最小二乘平差，再搜索宽巷观测值的整周模糊度。

GPS伪距双差观测方程可表示为：

GPS载波相位宽巷双差观测方程可表示为：

BDS载波相位宽巷双差观测方程可表示为：

式中，C为GPS伪距双差观测值，分别为GPS的L1、L2和BDS的B1、B2载波组成的双差宽巷观测值，ρGPS、ρBDS分别为GPS和BDS双差几何距离，［δXδYδZ］为流动站坐标改正值，［lGPSmGPSnGPS］、［lBDSmBDSnBDS］分别为测站至GPS和BDS卫星的方向余弦之差分别为和载波宽巷波长，分别为和载波宽巷整周模糊度，分别为各观测方程的残差项。

组合系统双差伪距和宽巷载波观测方程为：

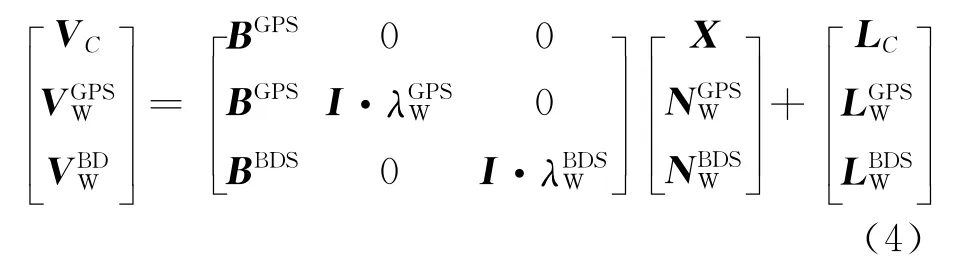
当观测方程个数不少于未知数个数时，可进行最小二乘求解：

P为权阵，可根据3类观测值的精度来确定，本文采用经验，按高度角和验后方差估计来确定。

在计算不同随机模型下宽巷模糊度的搜索空间［5］时，用高斯整数迭代法生成整数变换矩阵Z，对实数解模糊度和模糊度协方差进行去相关处理：

模糊度的搜索空间为：

式中，NZ为待定的整周模糊度，χ为χ2分布的置信系数。

由于伪距观测值精度低，经最小二乘解出来的宽巷模糊度浮点解精度差，模糊度的搜索空间大，增加了模糊度的固定难度。本文采用分组逐步固定模糊度，先选择方差较小的模糊度组成主模糊度组（大于3个），并得到主模糊度组的实数解和协方差阵，采用LAMBDA 方法对主模糊度进行解算［6］。当主模糊度组固定为整数向量后，转化成精度较高（相对于伪距观测值）的距离观测值，回代双差观测方程。用固定的这部分宽巷模糊度更新观测方程，可以改进所有的参数，包括从模糊度组参数，求得从模糊度实数解及其方差。再使用LAMBDA 方法，得到从模糊度组的固定解，进而将宽巷模糊度组合固定下来。

1.2 双差L1、L2、B1、B2 模糊度固定

双差宽巷模糊度固定后，双差宽巷观测值、L1和B1观测方程为：

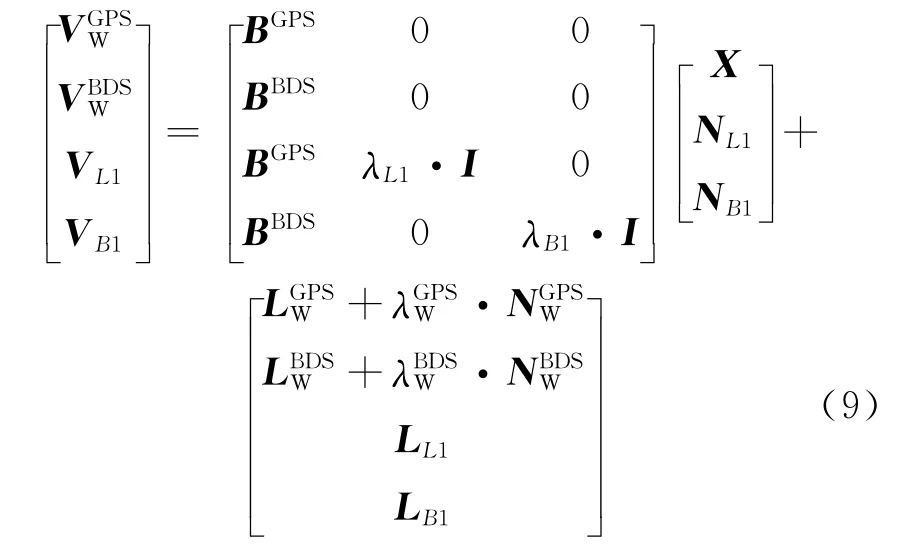
式中，VL1、VB1为双差观测值L1、B1的改正数，λL1、λB1为载波L1、B1的波长，NL1、NB1为双差观测值L1、B1的整周模糊度，LL1、LB1为双差观测值L1、B1的常数项。采用与式（4）相同的方法进行最小二乘解算，得到L1、B1的双差模糊度实数解及协方差阵，再对模糊度进行分组逐步固定。NL1、NB1准确固定后，L2、B2的双差模糊度NL2、NB2为：

2 GPS／BDS组合系统观测值随机模型的确定

2.1 经验随机模型

在经验模型中，观测值之间的权比按伪距的码元宽度和载波波长来确定，并认为观测值间相互独立。如GPS中的CA 码码元宽度为293.05m，按测距精度为码元宽度1%计算，其测距精度为2.931m。按载波测距精度为1%周，由L1、L2和B1、B2形成的宽巷观测值的波长分别为0.862m 和0.847m。式（4）中有3类观测值，于是P可设成如下形式：

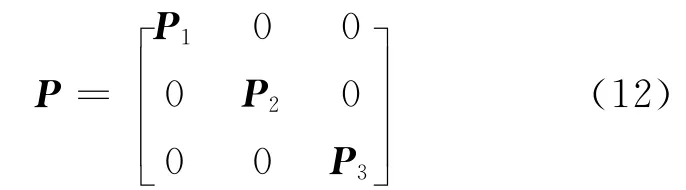
式中，P1设为单位阵，

2.2 基于高度角的随机模型

经验模型中，同一系统的同类观测值精度相同。而在实际中，不同卫星因高度角不同，受到的与传播路径有关的误差也不同。在基于高度角的随机模型中，卫星高度角越小，观测值受各种误差的影响就越大，精度越低。通常用正弦函数来计算各个非差观测值的方差：

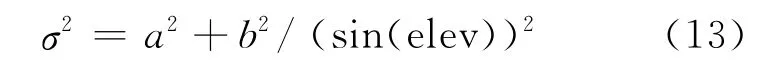
例如，对于GPS 系统双差相位观测值的方差－协方差阵可表示为：

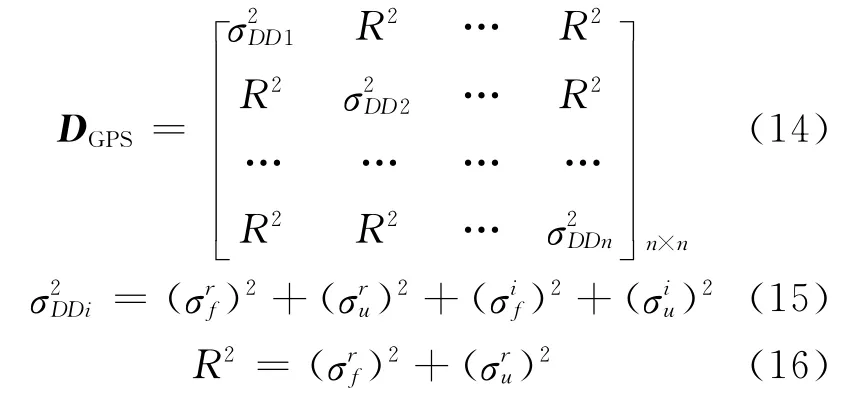
2.3 验后方差随机模型

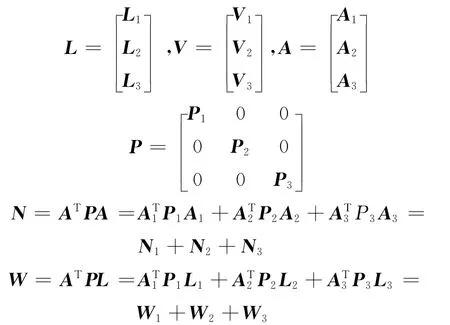
由于最小二乘残差能够较好地反映定位系统观测值的统计特征，而赫尔默特验后方差估计正是利用预平差的改正数V，按验后方差估计各类观测量验前方差，合理确定两个系统观测值的权阵［6］。

且有下列关系式：

3 实例分析

为研究以上3种随机模型对单历元基线解算的具体影响，本文先分析3种随机模型的模糊度搜索空间大小和模糊度搜索的成功率。模糊度搜索失败的可能原因有：确定的搜索空间内没有真值；观测值中含有粗差；模糊度搜索空间过大，出现多极值；搜索空间内有真值，但真值未通过F检验［8］。

文中先对一条零基线观测数据进行基线解算。该基线在2013－08－28用GPS／BDS双星接收机测定，历元采样率为10s。取1 000个历元进行解算。本时段中，对6颗GPS卫星（卫星号3、6、13、16、19、27）和6颗BDS卫星（卫星号1、2、3、7、8、10）进行持续观测，共有10个双差模糊度，得到实数解后选择方差较小的5个双差模糊度为主模糊度组。根据式（8）计算的模糊度搜索空间如表1所示。

表1 不同随机模型下宽巷模糊度的搜索空间大小Tab.1 The search space size of wide lane ambiguity aboutdifferent stochastic model

从表1可看出，不同的随机模型对组合系统单历元模糊度搜索成功率的影响不同。与经验模型和高度角模型相比，采用Helmert模型来确定观测值随机模型，模糊度搜索的空间最小。表2列出了应用不同随机模型进行单历元模糊度搜索的成功率。

表2 不同随机模型单历元模糊度搜索成功率Tab.2 The search success rate of single epoch ambiguity about different radon model

从表2看出，经验随机模型未考虑不同卫星信号传播过程中不同误差的影响，其模糊度搜索成功率最低。Helmert方差估计随机模型合理地确定了组合系统中不同系统、不同类型观测值之间的权比，其最小二乘解的残差反映了观测值的精度，提高了模糊度搜索的成功率。

为分析本文3种观测值随机模型对组合系统单历元基线解算精度的影响，分别给出3种随机模型下，单历元基线解的基线长偏差（基线长真值为0），如图1～3。

图1 经验随机模型基线向量X 方向偏差Fig.1 Baseline vector Xaxis deviation of experiential stochastic model

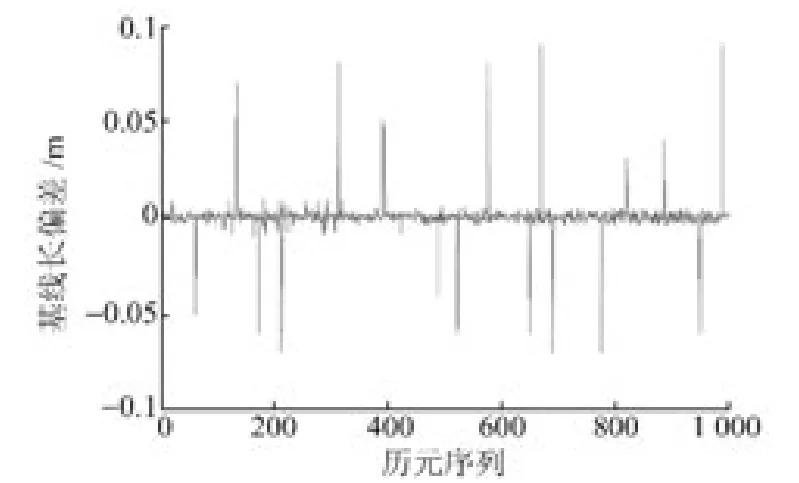
图2 高度角随机模型基线向量X 方向偏差Fig.2 Baseline vector Xaxis deviation of elevation angle stochastic model

图3 Helmert随机模型基线向量X 方向偏差Fig.3 Baseline vector Xaxis deviation of Helmert stochastic model

从图1～3中可看出，忽略未正确固定模糊度的历元，Helmert模型、高度角模型求解的单历元基线偏差均小于经验模型，其中Helmert模型基线偏差最小。

为统计基线解的精度，表3列出在忽略模糊度固定失败情况下不同随机模型单历元基线解的均值和方差。

表3 不同随机模型单历元基线长的均值、方差Tab.3 The mean value and variance of single epoch vector length about different radon model

从表3看出，不同的随机模型对单历元基线解的均值和方差均有不同的影响。由于是零基线，基线长均值可反映基线解的外符合精度。3种随机模型中Helmert模型外符合精度最高，其次为高度角模型。基线长方差反映了单历元基线解的内符合精度，3种随机模型中经验模型的方差要明显大于高度角模型和Helmert 模型，Helmert模型的方差要略小于高度角模型。

4 结 语

为拓展GPS／BDS组合系统在动态定位中的应用，本文研究了组合系统单历元基线解算中的模糊度固定方法，采用分组逐级固定的方法。实际处理结果显示，成功率达到96%以上。针对组合系统单历元基线解算中出现的来自不同系统、不同类型的观测值，以及如何确定最小二乘平差中观测值权阵的问题，本文提出采用Helmert验后方差估计的方法，并对比以往常用的经验模型和高度角模型。结果显示，Helmert模型能较合理地确定来自不同系统、不同类型观测值之间的权比，无论是单历元模糊度搜索成功率还是基线解的基线长偏差，均小于经验模型和高度角模型。

文中对信号易遮挡地区（如城市峡谷、山区）的组合系统单历元基线解算未有研究，对于不同模型的具体影响有待进一步研究。

［1］Han S，Rizos C.Single－Epoch Ambiguity Resolution for Real－Time GPS Attitude Determination with the Aid of One－Dimensional Optical Fiber Gryro［J］.GPS Solution，1999，3（1）：5－12

［2］Hartinger H，Brunner F K.Variances of GPS Phase Observations：the SIGMA－Model［J］.GPS Solutions，1999，2（4）：35－43

［3］戴吾蛟，丁晓利，朱建军.基于观测值质量指标的GPS观测量随机模型分析［J］.武汉大学学报：信息科学版，2008，33（7）：718－722（Dai Wujiao，Ding Xiaoli，Zhu Jianjun.Comparing GPS Stochastic Models Based on Observation Quality Indeces［J］.Geometics and Information Science of Wuhan University，2008，33（7）：718－722）

［4］祝会忠，高星伟，秘金钟，等.一种GPS 整周模糊度单历元解算 方 法［J］.测 绘 科 学，2011，36（4）：9－11（Zhu Huizhong，Gao Xingwei，Bei Jinzhong，et al.An Algorithm of GPS Ambiguity Resolution on Single－epoch［J］.Science of Surveying and Mapping，2011，36（4）：9－11）

［5］Teunissen P J G.Least－Squares Estimation of the Integer GPS Ambiguities［Z］.Delft Geodetic Computing Centre（LGR），1993

［6］Hofmann－Wellenhof B，Lichtenegger H，Wasle E.GNSSGlobal Navigation Satellite Systems：GPS，GLONASS，Galileo，and More［M］.New York：Springer，2007

［7］崔希璋，於宗俦，陶本藻，等.广义测量平差［M］.武汉：武汉大学出版社，2009（Cui Xizhang，Yu Zongchou，Tao Benzao，et al.Generalized Surveying Adjustment［M］.Wuhan：Wuhan University Press，2009）

［8］Verhagen S，Teunissen P J G.The Ratio Test for Future GNSS Ambiguity Resolution［J］.GPS Solutions，2013，17（4）：535－548