无模型自适应控制参数输入方法改进及在气体分馏装置操作调整中的应用
胡益民,李国庆,张家龙
(1华南理工大学化学与化工学院,广东 广州 510640;2中国石油天然气总公司锦西分公司,辽宁 葫芦岛125001)
无模型自适应控制参数输入方法改进及在气体分馏装置操作调整中的应用
胡益民1,李国庆1,张家龙2
(1华南理工大学化学与化工学院,广东 广州 510640;2中国石油天然气总公司锦西分公司,辽宁 葫芦岛125001)
无模型自适应控制(MFAC)不依赖受控系统的机理模型,只利用其输入输出(I/O)数据实现控制,近年来得到快速发展。本文用拟牛顿算法(BFGS)改进了MIMO系统MFAC算法的参数输入方法,以减少达到稳定操作的计算次数和调整时间,某30×104t·a−1气体分馏装置的应用表明,面对操作波动,改进后的MFAC能较快地实现操作稳定和质量达标;且由于不超调,塔底再沸和塔顶冷却负荷小,因而能耗低。
无模型自适应控制;过程控制;操作优化;过程系统;参数识别
引 言
现代控制理论是基于受控对象机理模型精确已知这个基本假设建立和发展起来的,因此被称为基于模型的控制(model based control, MBC)[1-2]。但随着工业设备越来越复杂,产品质量要求越来越高,过程机理精确建模已几乎不可能[3-5]。另一方面,工业过程却无时不在产生并储存着大量的数据,由于其包含了关于过程运行的全部信息,故能否直接利用它们进行控制呢?这就是所谓的数据驱动控制(data driven control, DDC)或无模型控制(mode-free control, MFC),即“控制器的设计仅利用受控系统的I/O数据,控制器中不包括受控过程的任何信息的控制理论和方法”[6-9]。
近年来,MFC得到了快速发展,形成了迭代反馈整定(iterative feedback tuning,IFT)、迭代学习控制(iterative learning control,ILC)、无模型自适应控制(model-free adaptive control,MFAC)、虚拟参考反馈整定(virtual reference feedback tuning,VRFT)等多种方法。其中MFAC由国内学者提出[10-14],意在用受控系统的I/O数据在线估计其伪偏导(pseudo partial derivative,PPD)和伪梯度(pseudo gradient,PG),从而在受控系统轨线附近用一系列的动态线性时变模型替代一般离散时间非线性系统,实现无模型自适应控制[15]。目前,该方法已成功应用于电力[16-18]、化工[19-21]、快速路交通控制[22-24]等领域。
1 复杂MIMO系统的MFAC控制算法
实际系统通常是多输入多输出(MIMO)的复杂系统,是由若干个子系统以串联、并联或反馈等形式连接而成的,若各子系统间的影响是可测的,则可将其分解[25](图1)。
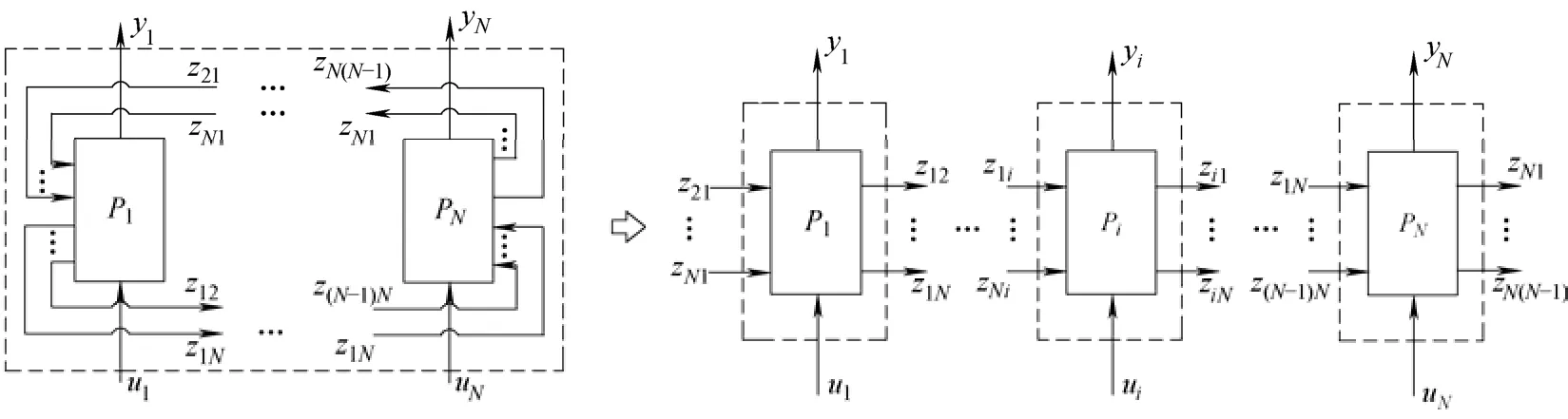
图1 复杂连接系统及分解Fig.1 Complex connection system and its decomposition



于是,复杂MIMO系统的MFAC可总结成如图2所示流程。

图2 复杂MIMO系统的MFAC流程Fig.2 MFAC working route of complex MIMO system
由图可知,复杂MIMO系统的无模型自适应控制的实质是利用系统在时刻1的伪梯度估计值(1)和权重、步长因子等,建立起系统在时刻0和1的初始输入值(ui(0)、ui(1))与对应的初始输出值(yi(1)、yi(2))之间的关系,并通过调整时变参数,使求得的预测输入ui(k)保证实际输出yi(k+1)不断朝期望输出逼近。
2 改进MFAC参数确定方法
从前面的说明可以看出,实现MFAC需知道系统在时刻1的伪梯度估计值(1)和权重、步长因子等参数,而这些参数对控制效果有着重大的影响。所以如何选取合适的参数,是关系到MFAC能否在实际工业生产中得到推广的关键。
每一个受控系统都有一组最符合其内在控制规律的参数(简称“最适参数”)。现有的MFAC并没有完善的参数选取方法,是随机选取,并通过时变的伪偏导(或伪梯度)来调整输入与输出之间的关系。这种参数选取方式存在着极大的不确定性,如果选取的参数与最适参数相差较大,那么即使通过时变的伪偏导(或伪梯度)来调整,仍难以达到对系统进行有效控制;如果选取的参数与最适参数较接近,就可以通过时变的伪偏导(或伪梯度)调整控制系统,较好地预测下一时刻的系统输出,从而使系统实际输出y(k+1)不断朝期望输出y∗(k+1)逼近。
本文对MFAC参数确定方法做如下改进:
(1)将系统初值从前两个时刻的历史数据(ui(0)、ui(1)、yi(1)、yi(2)、Δzji(1))扩大为前3个时刻的历史数据(ui(0)、ui(1)、ui(2)、yi(1)、yi(2)、yi(3)、Δzji(2));

改进参数确定方法后的MFAC流程如图3所示。
由图可知,相比于改进前的MFAC(图2),用拟牛顿法对前3个时刻的历史数据进行拟合,可以更有效的逼近最适参数;通过调整时变参数,就可以获得合适的预测输入u(k),以保证实际输出(1)y k+不断朝期望输出(1)y k∗+逼近,并最终达到。

图3 改进参数确定方法后的MFAC流程Fig.3 MFAC working route with new parameters input method
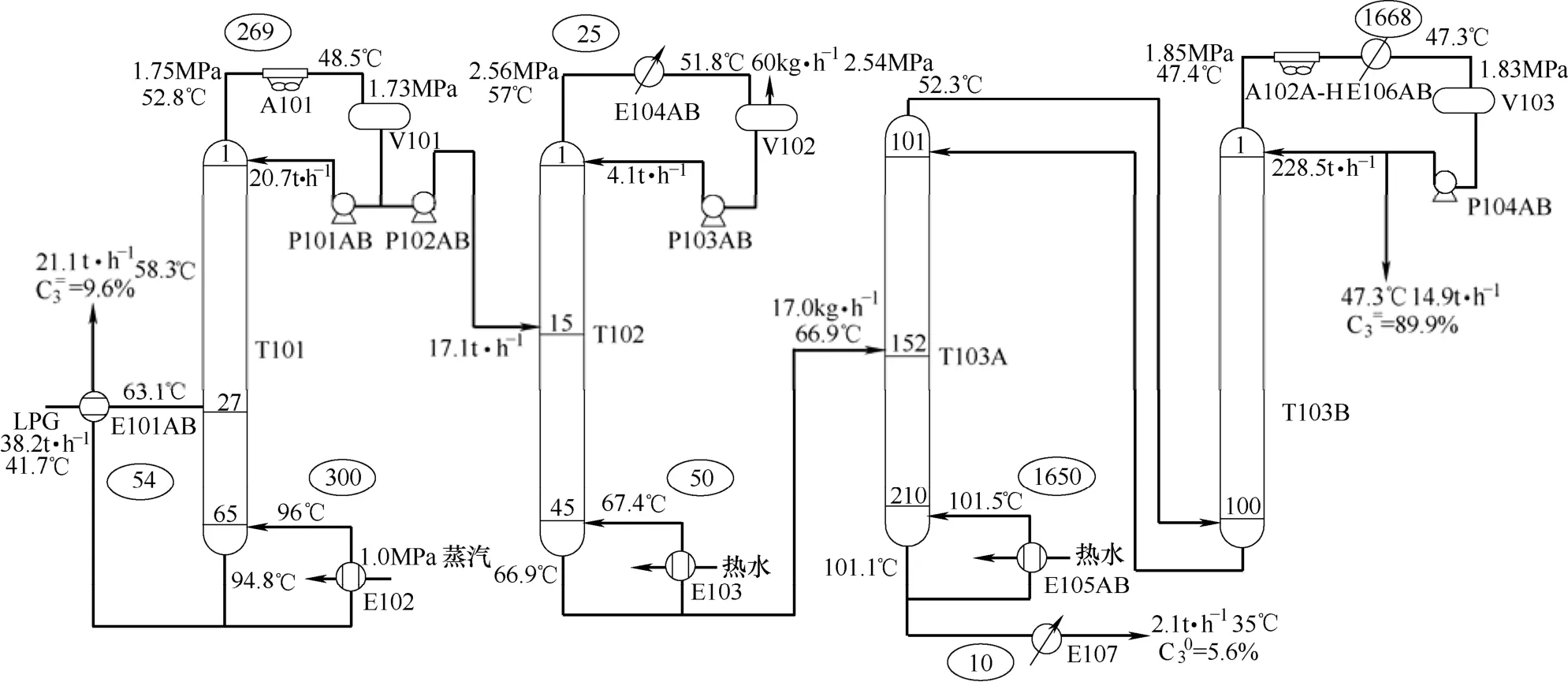
图4 某气分装置现有操作情况Fig.4 Present running situation of a gas fractionation unit
3 MFAC在气分装置生产操作中的应用
炼油厂气体分馏装置是利用精馏方法对产自催化裂化装置的液化石油气(LPG)进行精密分离,生产高纯度丙烯(摩尔浓度≥0.996)的装置(副产丙烷和混合C4)。由于被分离组分沸点接近(如其中丙烯、丙烷的常压沸点分别为−47.4℃和−42.09℃,45℃下的饱和蒸气压分别为1.81 MPa和1.51 MPa),故分离难度大,精馏级数多(特别是其中分离丙烯和丙烷的丙烯塔,其塔板数在200~240层之间,需两塔串联),回流比大,能耗高;且一旦操作波动,较难恢复稳定。
图4是某30×104t·a−1气分装置的操作示意。
图中,来自原料罐、摩尔组成如表1所示的38.2 t·h−1原料LPG从塔T101第27板进料,经脱丙烷塔、脱乙烷塔、丙烯塔分离后,得到丙烯摩尔浓度为0.096的混合碳四21.1 t·h−1,丙烷摩尔浓度为0.056的丙烷产品2.1 t·h−1以及丙烯摩尔浓度为0.899的丙烯产品14.9 t·h−1。由于丙烯产品中的丙烯纯度为0.899,小于质量控制指标0.996,故需做操作调整。
常规的调整方法是增加回流比。为此,增大塔底再沸器的蒸汽流量或热水流量,以及塔顶冷凝冷却器的循环冷却水流量,然后在保持各产品产量稳定的前提下增大塔顶回流量。在装置操作稳定,即塔压、进料情况、各产品产量等条件不变时,塔底再沸负荷决定塔顶冷却负荷以及回流量,从而决定回流比。
为了得到符合质量要求的产品,各塔需要在合适的操作条件下稳定运行。特别是回流比对产品质量影响很大。回流比偏小,产品纯度不达标;但当纯度达到一定程度时,回流比增大对纯度影响不大,但会增大能耗;回流比波动较大的时候,不仅产品质量不达标,操作人员还得经常进行手动调整,工作量大。所以可以通过无模型自适应控制,实时调整、优化回流比,使各产品达标,同时还避免塔底过度加热,增加能耗。
图4气分装置由三塔组成,是MIMO系统,存在塔间互联影响,所以在设计控制方案时,先要做分解(图5)。

表1 原料LPG的摩尔组成Table 1 Molar composition of LPG

图5 气分装置的分解Fig.5 Decomposition of gas fractionation unit
根据操作情况,本文定义脱丙烷塔(T101)的塔底再沸负荷QH1为u1、塔底产品混合C4中丙烯的摩尔浓度为1y;H1Q变化所引起的下游脱乙烷塔(T102)进料中2C组分的浓度变化为12z、丙烯塔(T103A)进料中丙烯的浓度变化为13z。脱乙烷塔塔底再沸负荷H2Q为2u,脱乙烷塔底产品中2C组分的浓度为2y,H2Q变化所引起的丙烯塔进料中丙烯的浓度变化为23z。丙烯塔塔底再沸负荷H3Q为3u,塔顶产品中丙烯的摩尔浓度为3y。
3.1 改进前后的MFAC方案在气分装置操作调整中的效果比较
为验证改进后的MFAC方案的优越性,结合流程模拟软件,分别给出改进前后两种MFAC方案在气分装置操作调整中的控制效果对比试验。
两种MFAC方案的初始输入值、初始输出值以及子系统间的可测互联影响变化值都通过流程模拟获得。改进前的MFAC方案为:u1(0)=3、u2(0)=0.5、u3(0)=16.5、u1(1)=3.2、u2(1)=0.6、u3(1)=16.7、y1(1)=0.096、y2(1)=0.001、y3(1)=0.899、y1(2)=0.068、y2(2)=0.001、y3(2)=0.928、Δz12(1)=0、Δz13(1)=0.021、Δz23(1)=0.021;改进后的MFAC方案为:u1(0)=3、u2(0)=0.5、u3(0)=16.5、u1(1)=3.2、u2(1)=0.6、u3(1)=16.7、u1(2)=3.4、u2(2)=0.7、u3(2)=16.9、y1(1)=0.096、y2(1)=0.001、y3(1)=0.899、y1(2)=0.068、y2(2)=0.001、y3(2)=0.928、y1(3)=0.042、y2(3)=0、y3(3)=0.956、Δz12(2)=0、Δz13(2)=0.02、Δz23(2)=0.02。
在参数设置方面,改进前的MFAC方案随机选择一组较优参数为:η1=0.5、ρ1=0.9、λ1=0.0001、μ1=1000、η2=0.5、ρ2=0.9、λ2=0.0001、μ2=1000、η3=0.5、ρ3=0.9、λ3=0.0001、μ3=1000、、

表2 两种MFAC方案在气分装置操作调整中的控制效果对比Table 2 Control effects of two kinds of MFAC schemes in gas fractionation unit
3λ=2.7697×10−5、3μ=3638、、。
将上述两组参数分别按图2、图3流程建立起各自的MFAC控制系统。表2是两种MFAC方案的控制效果对比。
两种MFAC方案中丙烯纯度在整个操作调整过程中的变化趋势如图6所示。
从图可以看出,改进后的MFAC方案,相比于改进前,其操作调整过程跟踪效果更好,很快实现操作稳定,且没有超调现象,不仅能通过自动调节塔底再沸负荷而使丙烯纯度达到期望值,而且还自动寻找到最适的塔底加热负荷QH1、QH2和QH3值,从而减少能耗。

图6 操作调整过程中的丙烯纯度跟踪图Fig.6 Trace diagram of propylene concentration in operation adjusting
3.2 改进的MFAC方案在气分装置操作稳定中的应用
实际生产中,气分装置各个塔的回流比通常会波动,影响产品质量。手工调节不但工作量大,而且还不够精确,并可能发生超调等问题。而应用MFAC并结合模拟软件,可实时优化塔底再沸负荷控制,从而稳定塔的操作。下面在3.1中改进的MFAC案例的基础上,说明改进后的MFAC方案在气分装置操作稳定中的作用。控制结果如表3所示。
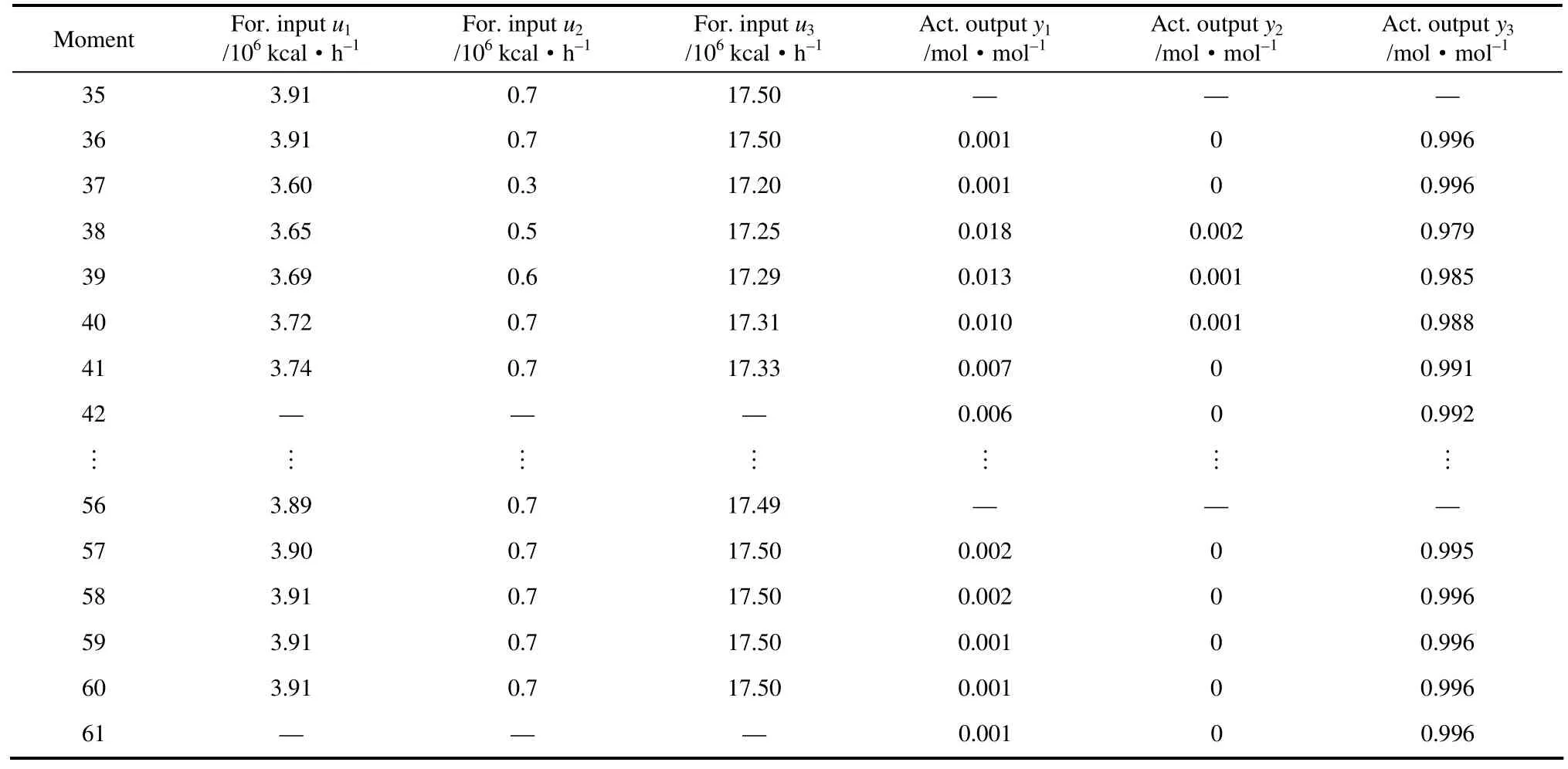
表3 气分装置维持稳定运行时预测输入与实际输出之间的关系Table 3 Relationship between forecast inputs and actual outputs when maintaining stable operation of gas fractionation unit
可见,在已达到产品纯度要求并稳定运行的气分装置中,在塔压及各产品产量不变的情况下,在第37时刻时,各塔底再沸负荷产生波动,使回流比降低,得到相应的实际输出为y1=0.018、y2= 0.002、y3=0.979。之后,系统自动对各塔底再沸负荷进行调整,增大回流比,使得系统的实际输出在58时刻后都达到目标值,并将其稳定在该值。整个控制过程丙烯纯度跟踪变化趋势如图7所示。
从图可以看出,当各塔底再沸负荷波动,进而影响丙烯纯度时,系统能够自动对再沸负荷进行调整,使输出值最终稳定在期望值,且整个控制过程的跟踪效果很好。这证明MFAC能够很好地根据历史数据自动调整操作并维持稳定运行,保证目标输出稳定在期望值。

图7 回流比波动时丙烯纯度跟踪性能图Fig.7 Trace diagram of propylene concentration upon reflux ratio’s fluctuation
4 结 论
气分装置生产高纯度丙烯(摩尔浓度≥0.996),装置整体能耗高、操作发生波动后难稳定,其传统的调节控制方式不仅工作量大,而且不精确,常发生超调等问题。将改进后的无模型自适应控制方法应用于气分装置的控制,从控制过程建立和控制结果来看,具有明显优势:
(1)控制器设计仅需I/O测量数据、无需任何模型的信息,传统的未建模动态问题在数据驱动的MFAC框架下并不存在,适用于复杂工业控制系统的实时优化;
(2)改进参数确定方法的MFAC可以更有效地调节塔底再沸负荷使系统实际输出达到期望值,拥有更强的控制能力,不存在超调现象,且整个过程自动运行,无需人工干预;
(3)当气分装置的系统输出达到期望值之后,改进的MFAC会将各塔底再沸负荷自动稳定在当前状态,从而使装置保持在能耗最低的情况下稳定运行;
(4)当因各塔再沸负荷产生波动(如蒸汽、热水量波动)而影响系统的输出数据时,改进的MFAC可以自动对其进行调整,使输出数据重新达到期望值,这提高了装置运行的平稳性,并减少了操作人员的工作强度。
符 号 说 明
u(k)——系统在k时刻的输入
y(k)——系统在k时刻的输出
y∗(k+1)——系统在k+1时刻的期望输出
zji(k)——第j个子系统对第i个子系统的可测互联影响
μ,λ——权重因子
ρ,η——步长因子
ϕc(k)——系统数据模型中的PPD在第k时刻的值
(k)——系统数据模型中的PPD在第k时刻的估计值
ϕji(k)——fi(...)对可测互联影响zji(k)的PPD
(k)——fi(...)对可测互联影响zji(k)的PPD的估计值
[1] Kalman R E. A new approach to linear filtering and prediction problems [J].Transactions ASME,Series D,Journal of Basic Engineering, 1960, 82: 34-45.
[2] Kalman R E. Contributions to the theory of optimal control [J].Boletin de la Sociedad Matematica Mexicana, 1960, 5: 102-119.
[3] Zeng Qingguo (曾庆国), Xing Guiju (邢桂菊), Wang Zhongchu (王仲初). Research and application of mode free adaptive control [J].Industrial Control Computer(工业控制计算机), 2009, 22 (6): 49-50.
[4] Anderson B D O. Failures of adaptive control theory and their resolution [J].Communications in Information and Systems, 2005, 5 (1): 1-20.
[5] Anderson B D O, Dehghani A. Challenges of adaptive control-past, permanent, and future [J].Annual Reviews in Control, 2008 32 (2): 123-135.
[6] Van Helvoort J. Unfalsified control: data-driven control design for performance improvement [D]. Eindhoven Technische Universiteit PHD Dissertation, 2007.
[7] Hou Zhongsheng (侯忠生), Xu Jianxin (许建新). On data-driven control theory: the state of the art and perspective [J].Acta Automatica Sinica(自动化学报), 2009, 35 (6): 650-667.
[8] Van Heusden K. Non-interative date-driven model reference control[D]. Lausanne:Ecole Polytechnique Federale de Lausanne PHD Dissertation, 2010.
[9] Hou Z S, Wang Z. From model-based control to date-driven control:survey, classification and perspective [J].Information Sciences, 2013, 235: 3-35.
[10] Hou Zhongsheng (侯忠生). Parameters identification of nonlinear systems, adaptive control and mode-freel adaptive control [D]. Shenyang: Northeastern University PHD Dissertation, 1994.
[11] Hou Zhongsheng (侯忠生). Nonparametric Model and Adaptive Control Theory (非参数模型及其适应控制理论) [M]. Beijing: Science Press, 1999.
[12] Hou Z S, Jin S T. A novel date-driven control approach for a class of discrete-time nonlinear systems [J].IEEE Transactions on Control Systems Technology, 2011, 19 (6):1549-1558.
[13] Hou Zhongsheng (侯忠生), Han Zhigang (韩志刚). Robust modelless learning adaptive of nonlinear systems [J].Control and Decision(控制与决策), 1995, 10 (2): 137-142.
[14] Hou Z S, Jin S T. Date driven model-free adaptive control for a class of MIMO nonlinear discrete-time systems [J].IEEE Transactions on Neural Networks, 2011, 22 (12): 2173-2188.
[15] Hou Zhongsheng (侯忠生). On model-free adaptive control: the state of the art and perspective [J].Control Theory & Applications(控制理论与应用), 2006, 23 (4): 586-592.
[16] Cao Rongmin (曹荣敏), Hou Zhongsheng (侯忠生), Bai Xuefeng (白雪峰), Huang Jian (黄健). DC motor speed regulating control system based on the model-free adaptive control method [J].Electric Drive(电气传动), 2008, 38 (7): 26-30.
[17] Cao Rongmin (曹荣敏), Hou Zhongsheng (侯忠生). Study of model-free adaptive control method in permanent magnet linear motor [J].Computer Engineering and Design(计算机工程与设计), 2007, 28 (6): 1433-1436.
[18] Tan K K, Lee T H, Huang S N,et al. Adaptive-predictive control of a class of SISO nonlinear systems [J].Dynamics and Control, 2001, 11 (2): 151-174.
[19] Shen Ji (沈继), Yu Jinshou (俞金寿). The application of the MFA control technology in temperature control of polymeric reactor [J].Automation in Petro-Chemical Industry(石油化工自动化), 2010, 6: 40-44.
[20] Cao Rongmin (曹荣敏), Hou Zhongsheng (侯忠生). Model-free learning adaptive control of a pH neutralisation Process [J].Computer Engineering and Applications(计算机工程与应用), 2006, 42 (28): 191-194.
[21] Coelho L D S, Pessoa M W, Sumar R P,et al. Model-free adaptive control design using evolutionary-neural compensator [J].Expert Systems with Applications, 2010, 37 (1): 499-508.
[22] Chi Ronghu (池荣虎), Hou Zhongsheng (侯忠生). A model-free periodic adaptive control for freeway traffic density via ramp metering [J].Acta Automatica Sinica(自动化学报), 2010, 36 (7): 1029-1032.
[23] Chi R H, Hou Z S. A model free adaptive control approach for freeway traffic density via ramp metering [J].International Journal of Innovative Computing,Information and Control, 2008, 4 (11): 2823-2832.
[24] Hou Zhongsheng,Yan Jingwen. Model free adaptive control based freeway ramp metering with feedforward iterative learning controller [J].Acta Automatica Sinica, 2009, 35 (6): 588-595.
[25] Hou Zhongsheng (侯忠生), Jin Shangtai (金尚泰). Model-free Adaptive Control—Theory and Application (无模型自适应控制——理论与应用) [M]. Beijing: Science Press, 2013.
Revamping of parameter input of MFAC and utilization in gas fractionation unit
HU Yimin1, LI Guoqing1, ZHANG Jialong2
(1School of Chemistry & Chemical Engineering,South China University of Technology,Guangzhou510640,Guangdong,China;2Jinxi Subsidiary of Petrochina Company Limited,Huludao125001,Liaoning,China)
In recent years, model-free adaptive control (MFAC) harvests a rapid development because it does not require the mathematical model and only uses the input/output data of the controlled system. In this paper the Quasi-Newton Methods (BFGS) was used to revamp the parameter input of MFAC of MIMO systems, resulting in less iterative calculating number of times and adjusting time. The application in a gas fractionation unit with an annual processing capacity of 0.3 Mt showed that MFAC can reach propylene quality target and steady operation rapidly with less energy consumption due to the minimum heating and cooling duties when facing operation fluctuation.
model-free adaptive control (MFAC); process control; operation optimization; process systems; parameter identification
LI Guoqing, gqli1@scut.edu.cn
10.11949/j.issn.0438-1157.20150091
TP 273
:A
:0438—1157(2015)10—4076—09
2015-01-20收到初稿,2015-06-08收到修改稿。
联系人:李国庆。
:胡益民(1989—),男,硕士研究生。
Received date: 2015-01-20.

