改进的经验正交函数分析方法及其效果验证

罗小莉,李丽平,王盘兴,周国华,谢瑶瑶

(1.广西壮族自治区气象服务中心,广西 南宁 530022;2.气象灾害教育部重点实验室(南京信息工程大学),江苏 南京 210044;3.南京信息工程大学 大气科学学院,江苏 南京 210044;4.扬州市气象局,江苏 扬州 225009;5.湖北省气象局,湖北 武汉 430074)



改进的经验正交函数分析方法及其效果验证

罗小莉1,2,3,李丽平2,3,王盘兴2,3,周国华4,谢瑶瑶5

(1.广西壮族自治区气象服务中心,广西 南宁 530022;2.气象灾害教育部重点实验室(南京信息工程大学),江苏 南京 210044;3.南京信息工程大学 大气科学学院,江苏 南京 210044;4.扬州市气象局,江苏 扬州 225009;5.湖北省气象局,湖北 武汉 430074)

基于中国站点网气候资料,简要介绍了经验正交函数(empirical orthogonal function,EOF)与改进的经验正交函数(adjusted EOF,AEOF)分析方法的关系,给出了验证其分析效果的方案;并将EOF、AEOF分析方法应用于中国160站60 a(1951—2010年)夏季气温距平场序列的分析。结果表明:AEOF分析方法前6个模态的模方拟合率和累积模方拟合率均高于EOF分析方法的相应量;AEOF分析方法前3个模态的典型场对夏季气温距平场序列的模方场的拟合效果明显优于EOF分析方法。由此论证了EOF分析方法中资料均匀化订正的必要性,验证了实际分析中AEOF分析方法的较优效果。

站网资料均匀化订正;改进的经验正交函数分析方法;效果验证;中国夏季气温距平场序列

0 引言

众所周知,Lorenz(1956)将经验正交函数(empirical orthogonal function EOF)分析方法引入大气科学分析,Craddock and Flood(1969)和Kutzbach(1970)将其用于气候资料时间序列的实际分析,EOF分析方法现已成为大气环流和气候异常分析中应用最广泛的分析方法之一(傅云燕等,2013;郭志荣等,2014;孟莹莹等,2014;赵佳莹和徐海明,2014;朱伟军等,2014)。按随机函数论(卡札凯维奇,1974),EOF分析方法用于气候问题分析时,要求气候资料序列在时间和空间域上满足均匀性。而格(站)点网上的气候资料一般能满足时域上的均匀性,但却很难严格满足空域上的均匀性,后者指每个格(站)点代表的区域面积相等。研究发现,直接对这种气候资料作EOF分析,得到的结果必然是失真的(Buell,1971,1978;Dyer,1975;Morin et al.,1979;Karl et al.,1982)。

为解决这一问题,已提出了许多订正方法(Craddock and Flood,1969;Kutzbach,1970;邓爱军等,1989;Kushnir and Wallace,1989;丁裕国和江志红,1995;李栋梁等,1995;Mitchell and Blier,1997;Chung and Nigam,1999),它们可归纳为两大类:一类是从现有格(站)点网中按均匀性要求经验地选择部分格(站)点组成新格(站)点网,使新格(站)点网具有近似的均匀性,EOF分析对新格(站)点网上的资料进行。如Kutzbach(1970)在分析1、7月北半球海平面气压距平场多年序列时,新格点网由相对均匀分布的180个格点组成,李栋梁等(1995)在研究中国夏季月平均气温异常时,从160站站网中选取40个分布较均匀的测站构成新站点网;EOF分析对新格、站点网上的资料进行。这类订正方法容易实施,但新格(站)点分布并不严格均匀,且订正中会随舍去格(站)点而损失有价值的气候信息。另一类是直接对格(站)点网所有资料作权重订正(Kushnir and Wallace,1989;Mitchell and Blier,1997;Chung and Nigam,1999),权重与格(站)点代表的面积有关,EOF分析对新格、站点网上订正后的资料进行。如Chung and Nigam(1999)给出了均匀经纬格点网资料EOF分析中的均匀化订正方案;王盘兴等(2011)、罗小莉等(2011)给出了站点网(如中国160站站网)资料EOF分析中的均匀化订正方案。这类订正方法符合数学理论要求。称Chung and Nigam(1999)与王盘兴等(2011)提出的方法为改进的经验正交函数(adjusted empirical orthogonal function,AEOF)分析方法。

本文简要介绍AEOF分析方法。在此基础上,以罗小莉等(2011)的工作为例,重点论证EOF分析方法中资料均匀化订正的必要性,验证实际分析中AEOF分析方法的效果优于EOF。

1 AEOF分析方法原理

选择距平场时间序列

(1)

为分析对象。其中:m为F′ 的场点数;n为时间序列长度。它的协方差矩阵为

(2)

T为矩阵转置符号。A的s1行、s2列元素As1s2是s1、s2点F′序列的协方差。

1.1 经验正交函数分析方法(EOF)

F′ 的EOF分析指对F′ 的如下正交分解

(3)

(4)

1.2 改进的经验正交函数分析方法(AEOF)

按随机函数论(卡札凯维奇,1974),(1)式的F′是连续域D上的母体距平随机函数场演变

f′(s,t)(s∈D,t∈T)

(5)

的离散化近似。(2)式的A是连续域上协方差场集

(6)

的离散化近似。若离散过程中面元Δs、Δt均匀且足

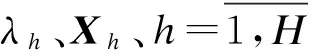
(7)

用w求得F′、A的订正结果

(8)

AEOF分析得

(9)

(10)

(11)

2 AEOF分析方法效果验证方案

理论上,AEOF分析方法无疑优于EOF方法,问题是,在实际分析中怎样验证其改进效果。这里,以中国160站60 a(1951—2010年)夏季气温距平场序列EOF分析为例,从模方拟合率和空域特征两个最基本的方面进行比较,验证AEOF分析方法的优越性。

2.1 模方拟合率比较方案

(12)

(13)

(14)

2.2 空域特征比较方案

以V记F′的行向量模方场,它是由A主对角元素构成的向量

V=(A11A22…Amm)T。

(15)

其s点值为

(16)

它给出了s点F异常强弱的度量。

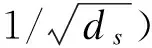
(17)

3 应用举例

3.1 模方拟合率比较

3.2 空间特征比较

由图1可见,中国夏季气温异常强度随纬度增大,东西向比较均匀。全国约分为3带:27.5°N以南为低异常带;40.0°N以北为高异常带,尤以东北、华北北部为大;27.5～40.0°N间为中等异常带。

表1 1951-2010年中国夏季气温距平场序列和经EOF、AEOF分析的方差贡献Table1 Variance contributions of EOF and AEOF analysis for the anomalous summer air temperature seriesadnin China during 1951-2010 %

图1 1951—2010年中国夏季气温距平场序列的模方场V(单位:℃2;浅阴影表示值大于20 ℃2,深阴影表示值大于40 ℃2)

图2 1951—2010年中国夏季气温距平场序列的EOF特征向量场(单位:℃;图中等值线值扩大至10倍;深阴影表示值大于1 ℃,浅阴影表示值小于-1 ℃) a.X1;b.X2;c.X3

图3 1951—2010年中国夏季气温距平场序列的AEOF特征向量场(单位:℃;图中等值线值扩大至10倍;深阴影表示大于2 ℃,浅阴影表示小于-2 ℃

因此,就空间特征而言,AEOF分析明显优于EOF分析(罗小莉等,2011;王盘兴等,2011)。出现这种的结果,是由于站网均匀化订正增大了西北部测站的异常模方(ds大),减小了东南部测站的异常模方(ds小)。

4 结论

改进的经验正交函数(AEOF)分析方法,是对经过空间均匀化订正的格、站点网资料的EOF分析方法。本文简要介绍了站点网气候资料的AEOF与EOF分析方法的关系,给出了验证其分析效果的方案。将AEOF、EOF分析方法应用于中国160站60 a(1951—2010年)夏季气温距平场序列的分析,结果表明:1)AEOF分析方法前6个模态的模方拟合率和累积模方拟合率均高于EOF分析方法的相应量。2)AEOF分析方法前3个主要模态的典型场对夏季气温距平场序列模方场的拟合效果明显优于EOF分析方法。由此论证了EOF分析方法中资料均匀化订正的必要性,验证了实际分析中AEOF分析方法的效果。

致谢:基金委地学部南京大学资料服务中心提供了1951—2010年中国160站逐月平均气温资料,谨致谢。

邓爱军,陶诗言,陈烈庭.1989.我国汛期降水的EOF分析[J].大气科学,13(3):289-295.

丁裕国,江志红.1995.非均匀站网EOFs展开的失真性及其修正[J].气象学报,53(2):247-253.

傅云燕,杨修群,沈伟.2013.江苏省冬季气温、降水年代际异常及相关分析[J].气象科学,33(2):178-183.

郭志荣,陈旭红,江燕如,等.2014.中国东部夏季水汽输送的年代际变化特征[J].大气科学学报,37(5):568-574.

卡札凯维奇.1974.随机函数论原理及其在水文气象中的应用[M].章基嘉,译.北京:科学出版社:245-270.

李栋梁,吴洪宝,章基嘉.1995.中国夏季月平均气温异常研究[J].高原气象,14(2):165-175.

罗小莉,李丽平,王盘兴,等.2011.站网均匀化订正对中国夏季气温EOF分析的改进[J].大气科学,35(4):620-630.

孟莹莹,苗峻峰,徐祥德,等.2014.中国东部夏季主要降水型与高原春季热力因子间的关系[J].气象科学,34(4):373-382.

王盘兴,罗小莉,李丽平,等.2011.中国气候资料站网均匀化订正的一种方案及应用[J].大气科学学报,34(1):8-13.

赵佳莹,徐海明.2014.中国区域位势高度场探空与再分析资料的对比分析[J].气象科学,34(2):128-138.

朱伟军,胡瑞卿,徐明.2014.西北太平洋和南海不同时段生成热带气旋频数及其水汽条件的分类[J].大气科学学报,37(3):344-353.

Buell E C.1971.Integral equation representation for factors analysis[J].J Atmos Sci,28(8):1502-1505.

Buell E C.1978.The number of significant proper functions of two-dimensional fields[J].Appl Meteor,17(6):717-722.

Chung C,Nigam S.1999.Weighting of geophysical data in principal component analysis[J].J Geophys Res,104(D14):16925-16928.

Craddock J M,Flood C R.1969.Eigenvectors for representing the 500mb geopotential surface over the Northern Hemisphere[J].Quart J Roy Meteor Soc,59:576-593.

Dyer T G J.1975.Assignment of rainfall stations into homogeneous group:An application of PCA[J].Quart J Roy Meteor Soc,101(430):1005-1013.

Karl,T R,Koscielny A J,Diaz H F.1982.Potential error in the application principal component(eigenvector) analysis to geophysical data[J].J Appl Meteor,21(8):1183-1186.

Kushnir Y,Wallace J M.1989.Low-frequency variability in the North Hemisphere winter:Geographical distribution,structure and time-scale dependence[J].J Atmos Sci,46(20):3122-3142.

Kutzbach J E.1970.Large-scale features of monthly mean Northern Hemisphere anomaly maps of sea-level pressure[J].Mon Wea Rev,98(9):708-716.

Lorenz E N.1956.Empirical orthogonal functions and statistical weather prediction.Cambridge:Massachusetts Institute of Technology:49.

Mitchell T P,Blier W.1997.The variability of wintertime precipitation in the region of California[J].J Climate,10(9):2261-2276.

Morin G,Fortin J P,Sockanska W,et al.1979.Use of PCA to identify homogeneous precipitation stations for optimal interpolation[J].Water Resour Res,15(6):1841-1850.

(责任编辑：张福颖)

An adjusted empirical orthogonal function analysis method and its effect verification

LUO Xiao-li1,2,3,LI Li-ping2,3,WANG Pan-xing2,3,ZHOU Guo-hua4,XIE Yao-yao5

(1.Guangxi Meteorological Service Center,Nanning 530022,China;2.Key Laboratory of Meteorological Disaster(NUIST),Ministry of Education,Nanjing 210044,China;3.School of Atmospheric Sciences,NUIST,Nanjing 210044,China;4.Yangzhou Meteorological Bureau,Yangzhou 225009,China;5.Hubei Meteorological Bureau,Wuhan 430074,China)

Based on the climatic data of station network in China,this paper briefly describes the relationship between the empirical orthogonal function(EOF) analysis method and the adjusted EOF(AEOF) analysis method,and gives schemes of analysis effect verification.Using EOF and AEOF methods,this paper analyses the anomalous summer air temperature series at 160 stations in China during 1951—2010.Results show that the mode square fitting rate and the cumulative mode square fitting rate of the first six modes by AEOF method are higher than those by EOF method.The fitting effect of the typical fields of first three modes by AEOF method on the mode square field of anomalous summer temperature series are better than that by EOF method.Therefore,the necessity of station homogeneity adjustment is demonstrated when EOF method is used,meanwhile the better adjustment effects using AEOF method are verified in the actual analysis.

homogeneity adjustment of station network data;adjusted empirical orthogonal function analysis method;effects verification;anomalous summer air temperature series in China

2012-12-21；改回日期：2013-04-04

国家自然科学基金资助项目(41330425);国家重点基础研究发展计划(973)项目(2015CB453202);广西科学研究与技术开发计划项目(桂科攻1355010-4)

王盘兴,教授,博士生导师,研究方向为大气环流异常与短期气候预测,wangpx@nuist.edu.cn.

10.13878/j.cnki.dqkxxb.20121221006.

1674-7097(2015)01-0120-06

P468

A

10.13878/j.cnki.dqkxxb.20121221006

罗小莉,李丽平,王盘兴，等.2015.改进的经验正交函数分析方法及其效果验证[J].大气科学学报,38(1):120-125.

Luo Xiao-li,Li Li-ping,Wang Pan-xing,et al.2015.An adjusted empirical orthogonal function analysis method and its effect verification[J].Trans Atmos Sci,38(1):120-125.(in Chinese)