基于共有单平面的点云拼接技术研究
侯东兴 李宗春 邓 勇
1 信息工程大学地理空间信息学院,郑州市科学大道62号,450001
地面三维激光扫描技术是一种高效获取海量点云并运用点云数据处理软件进行数据预处理和三维建模的技术。点云拼接是三维激光扫描仪数据采集和处理中的关键环节,影响数据预处理和建模的精度,是激光扫描技术数据处理中的热点和难点[1-2]。点云拼接技术实质是坐标转换,而坐标转换常用的方法是通过寻找3对或者3对以上的公共点来计算坐标转换参数,完成坐标系的统一。在三维激光扫描模式下,公共点转换方法依然可行,但是寻求公共点并精确计算点的坐标费时费力,研究基于公共特征的坐标转换方法势在必行[3]。
扫描场景中广泛存在着平面特征。王力等[3]针对多平面特征的场景(平面数至少为3个),提出基于平面的坐标转换模型。目前,市场上扫描仪一般都具有整平和补偿功能,扫描测量中不同测站坐标系Z轴方向与铅垂线方向相反,即不同测站坐标系绕Z轴旋转即能满足三轴指向概略相同。基于此,本文提出基于共有单平面的点云拼接技术:首先进行平面的提取、拟合,精确计算平面的法向量;再运用平面的法向量信息,利用旋转角构造旋转矩阵;最后通过平面的中心点(视为公共点)进行坐标平移,完成点云拼接。
1 平面特征的提取
提取平面特征的方法一般分为人机交互法和平面特征自动提取算法等[4-6]。人机交互法是操作员通过计算机显示的扫描点云数据,将共有的平面点云提取出来,或者在扫描阶段对共有的平面进行单独扫描,直接将平面点云提取出来。自动提取算法包括以下两种。
1)基于法向量聚类的平面点云提取。平面特征自动提取需要提前获取平面的大致个数。平面点云中的点存在一个共同特性,即点的单位法向量基本相同,它们的单位法向量与平面的单位法向量一致。因此,可以采用聚类的算法(将单位法向量是否相同作为是否归为一类的评判标准)将平面提取出来。平面特征自动提取的步骤为:①对原始点云进行采样;②计算点云的单位法向量[7];③对点云的法向量进行聚类运算;④编号存储法向量相同的点云。
2)基于回光强度的平面点云提取[1-2]。三维激光扫描仪不仅记录目标点的三维坐标,还记录照射材料的回光强度。目前对回光强度的利用相对较少,大多数情况下仅仅用于点云的可视化。在不同于其他材质的平面特征中,人工标志的反射强度明显高于一般地物,可以利用点的回光强度值进行聚类,从而将平面自动提取出来。
2 平面拟合
2.1 求解平面参数[8-10]
平面拟合实质上是求解平面的最优参数。三维空间中平面的数学表达式一般为:ax+by+cz+d=0。该表达式唯一确定了一个平面,但是平面方程并不是只有一个这样的表达式(如2ax+2by+2cz+2d=0)。为了能让平面有唯一的表达式,定义平面方程为:
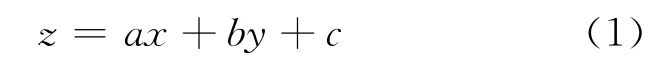
式中,a、b、c为平面拟合的待估参数(此平面不与XOY面平行)。
扫描仪获取的点坐标在x、y、z3个方向均存在误差,误差方程式为[11]:

式中,vxi、vyi、vzi为点坐标x、y、z3个方向的误差改正数。整理成误差方程向量形式:

取方程的最小二乘解作为参数的估值。考虑到系数矩阵和观测值中均含有误差,采用矩阵的SVD(奇异值分解)[8]法求解参数最小二乘解。步骤为:①组成增广矩阵,并进行奇异值分解,即,其中V=;②求解参数估值,如果V22非奇异,则;③进行精度评定。
2.2 优化平面参数
由于各种因素的影响,三维激光扫描仪获取的平面点云必然会存在粗差点,特别是在平面的边界区域。因此,为了获取较高精度的平面参数,需要对这些粗差点进行剔除,再进行平面参数的重新估值。粗差点的剔除主要根据点到拟合平面的距离进行判定。平面参数优化的具体步骤为。
1)计算点到平面的距离。引入点到平面的距离公式:
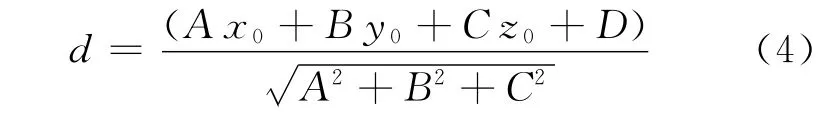
式中,A=a,B=b,C=-1,D=c。
2)应用贝塞尔公式计算距离中误差[11]:
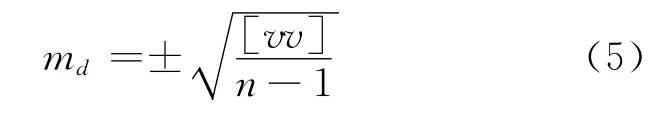
3)粗差点剔除。由于三维扫描仪获取的点云数据量大,粗差点数量不易估计,粗差点对初始平面参数的影响也不易估计。设置3md为极限误差来剔除粗差点,若di>3md,此点作为粗差点剔除。
4)重新计算平面参数。利用保留下来的平面点云和前文方法重新计算平面参数a、b、c。
5)迭代优化平面参数。设置3md为极限误差来剔除粗差点,将2md设置为一般误差来优化点云。利用优化的点云重新计算平面参数,将剔除粗差后的点云作为新的平面点云继续迭代优化计算。通过设置迭代次数阈值或者平面参数变化阈值,来完成平面参数的优化。
3 解算转换矩阵
3.1 计算旋转矩阵
平面的法向量可由平面参数来表示。平面法向量可表示为(a,b,-1)或(-a,-b,1),两种法向量方向相反。
不同测站下扫描获取的同一平面点云的法向量是不同的。假设测站1与测站2之间的旋转矩阵为R21(R21为3×3矩阵),那么一定满足(a1,b1,-1)=R21(a2,b2,-1)(设(a1,b1,-1)与(a2,b2,-1)同为背离测站方向或同为指向测站方向)。旋转矩阵具有3个自由度,如果只将法向量视为一个公共点坐标,是不能解出旋转矩阵的。平面的法向量由平面点云计算得出,所以不能只将法向量视为一个点坐标。
运用两个法向量求解一个旋转矩阵,使法向量重合有较多方法[12],其中较经典的是基于罗德里格矩阵求解旋转矩阵。其求解公式为:
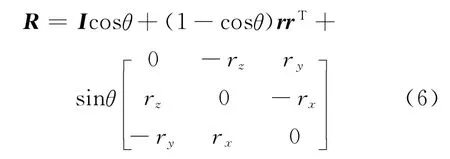
式中,I为单位阵,r为向量叉乘计算的单位向量,θ为向量之间的夹角。
此旋转矩阵R满足(a1,b1,-1)=R(a2,b2,-1)。但此旋转矩阵只是将平面的法向量方向重合,而没有将平面上的点云重合,不是欧氏空间转换的旋转矩阵。欧氏空间转换的旋转矩阵可由欧拉角、单位四元数、Kardan旋转(依次绕坐标轴Z、Y、X旋转)等方法得到[1]。已知同一平面在不同测站的法向量,可根据Kardan 旋转方法求取旋转矩阵。具体步骤如下。
1)统一两组法线方向(同为指向测站方向或同为背离测站方向),方法是构造一个向量来约束平面法线方向。向量的构造过程为:任取共有平面上一点P(也可取平面重心点或中心点),设测站坐标原点为S,连接P、S两点,方向指向测站方向(图1)。将构造的向量点乘平面法向量,如果不同测站点乘的结果符号相同,则将此时的法向量作为平面法向量;如果不同测站点乘的结果符号不同,则将其中一个测站的法向量的反向量作为平面的法向量,另一个测站的法向量不变,最终确保两个平面法向量相对于测站具有统一的指向。
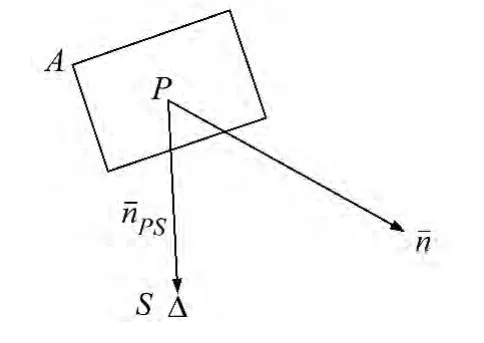
图1 构造的向量与平面法线的关系Fig.1 The relationship of constructed vector and plane normal
2)将不同测站共有平面的法向量绕Z轴旋转到XOZ面的第一象限,分别计算旋转后法向量与Z轴正方向的夹角α1、α2,计算待拼接测站坐标系绕Y轴旋转的角度Δα=|α1-α2|。
3)将不同测站的共有平面的法向量绕Z轴旋转到YOZ面的第一象限,分别计算旋转后法向量与Z轴正方向的夹角β1、β2,计算待拼接测站坐标系绕X轴旋转的角度Δβ=|β1-β2|。
4)若Δα<Δβ,分别计算不同测站的共有平面法向量在XOY面的投影与X轴正方向的夹角θ1、θ2;若Δα>Δβ,则分别计算不同测站的共有平面法向量在XOY面的投影与Y轴正方向的夹角θ1、θ2。
5)确定解算旋转矩阵。根据扫描仪特性,Δα、Δβ为较小的值。若Δα<Δβ,则将两个测站的坐标系分别绕Z轴旋转-θ1、-θ2,将平面法向量旋转到XOZ面内,再分别计算不同测站的共有平面法向量与X轴正方向的夹角,将两个测站的坐标系分别绕Y轴旋转将平面法向量旋转到与X轴平行,最后将待拼接测站坐标系绕X轴旋转Δβ=β1-β2。则:
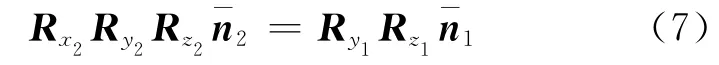
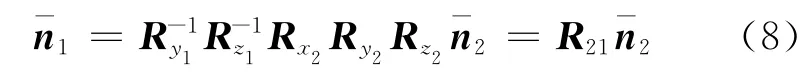
3.2 计算平移矩阵
共有平面在待拼接测站下的平面点云经过旋转后,与这个平面在固定测站下的平面点云平行,再经过平移即能完成平面点云的重合。平移矩阵需要一对公共点解算:
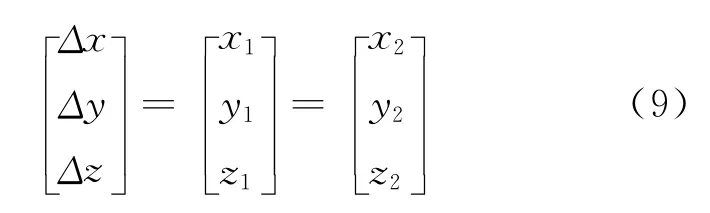
寻找公共点有多种方法,如将两个平面的中心或重心作为公共点,在扫描时测得一组公共点,或通过人机交互直接确定一组或几组公共点。公共点的坐标精度将直接影响点云拼接的精度。
4 基于共有单平面特征的点云拼接实验
4.1 仿真数据实验
利用VS2010编程,获取一个平面点云和一个半球形点云,视为第一测站点云数据。将第一测站点云数据经过坐标转换,作为第二测站点云数据。模拟两站点云数据如图2(a)所示。
第一测站点云经转换矩阵后形成第二测站点云,满足:

式中,P为第一测站点云,Q为模拟的第二测站点云。坐标转换矩阵如表1所示。
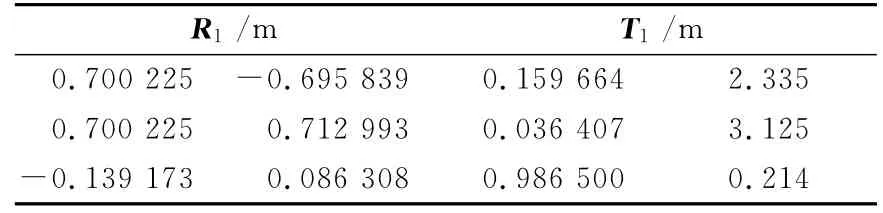
表1 生成第二测站点云的转换矩阵Tab.1 The transformation matrix of generating second station point cloud
经过平面提取、拟合,解算两站点云的旋转矩阵。将点云的重心作为公共点求解平移矩阵。利用求解出的转换矩阵,对第二测站点云进行坐标转换,转换后点云如图2(b)所示。

图2 模拟数据拼接实验Fig.2 Registration experiment by simulated data
平面导出的转换矩阵应满足:
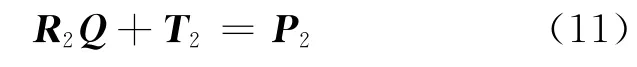
式中,Q为模拟的第二测站点云,P2为反求的第一测站点云。单平面求得的转换矩阵如表2所示。
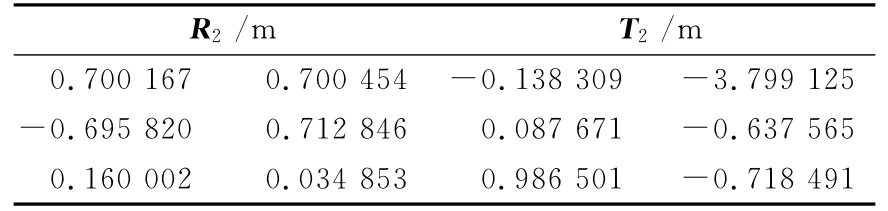
表2 单平面导出的转换矩阵Tab.2 The transformation matrix calculate by single plane
由式(10)和式(11)可导出,两组转换矩阵应满足:
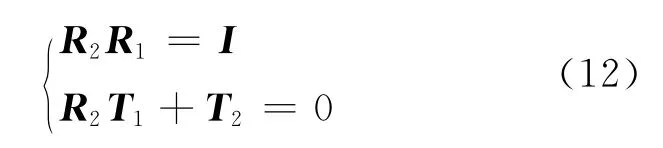
式中,I为单位阵。将两组转换矩阵代入式(12),求得的结果如表3所示。
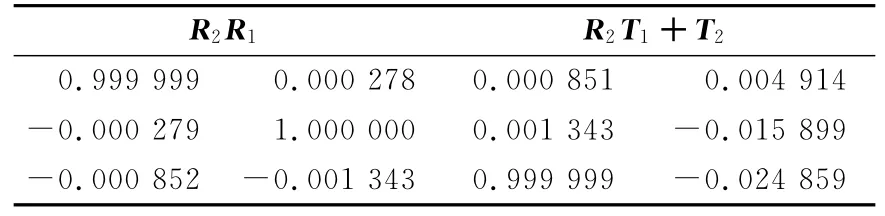
表3 R2R1 和R2T1+T2 的值Tab.3 The values of R2R1and R2T1+T2
从图2(b)可知,两站点云较好地拼接在一起。从表3可以推出,反求的转换矩阵是正确的。经过坐标差计算,两站模拟数据坐标差基本为0,证明了此方法的可行性。
4.2 实测数据实验
点云采用RIEGL VZ-400扫描仪获取,配套软件为RiSCAN-PRO。进行两组实验,实验1对方凳和仪器箱分别进行扫描,实验2对雕像进行扫描。平面点云提取方式为对共有的平面单独扫描,直接将平面点云提取出来(点云为方凳平面点云)。首先对点云进行均匀采样,保证一定数量的点云个数(数量过大,奇异值分解计算无法进行),求取最优的平面参数。然后,将求取的平面参数运用到原始点云中,进行粗差点剔除,将优化后的平面点云重心坐标作为公共点。
利用最优的平面参数和公共点解算转换矩阵,将转换矩阵应用到待拼接的点云中完成点云拼接。两站平面点云拼接前后分别如图4(a)、(b)所示。
实验1中,利用共有平面(方凳)导出的转换矩阵对仪器箱进行拼接,如图5所示。实验2中,利用共有平面(雕像基座)导出的转换矩阵对人物雕像进行拼接,如图6所示。从图4~6看出,不同站间点云比较好地拼接在一起,证明此方法正确可行。

图3 平面点云优化Fig.3 The optimization of plane point cloud

图4 平面点云拼接实验Fig.4 The registration of plane point cloud
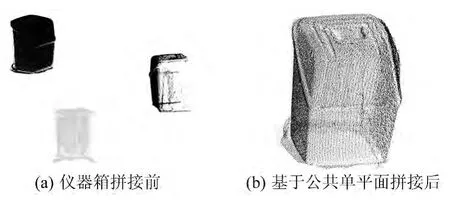
图5 基于平面的仪器箱拼接实验Fig.5 The registration of instrument container based on plane
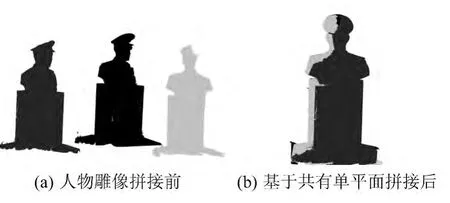
图6 基于平面的雕像拼接实验Fig.6 The registration of statue based on plane
5 结 语
基于共有单平面特征的点云拼接具有较强的适用性,模拟数据和实验数据均验证了本文算法的正确性和可靠性。由于测量误差的存在,提取的特征往往存在误差,相邻测站通过特征建立的关系模型也会存在模型误差,因此通过特征法得到的转换参数精度相对较低。在地形测量、工程测量、雕像建模、数字城市等领域,容易提取和应用的特征相对较多,特征拼接容易满足精度要求。但在文物保护、逆向工程等精度要求较高的领域,提取和使用的特征精度往往难以满足要求。将特征法和ICP 算法相结合,先用特征法进行粗拼接,作为ICP 的初始转换参数,然后再由ICP 迭代提高拼接精度。在下一步的工作中,将设计平面度较高的平面圆形靶标进行多站点云拼接,用以提高测量工作的效率。在多平面场景中,研究平面的自动匹配以及单平面与多平面坐标转换模型的组合求解。
[1]李广云,李宗春.工业测量系统原理与应用[M].北京:测绘出版社,2011(Li Guangyun,Li Zongchun.The Principles and Applications of Industrial Measuring Systems[M].Beijing:Survey and Mapping Press,2011)
[2]王力.基于人工标志的激光扫描数据自动拼接技术研究[D].郑州:信息工程大学,2010(Wang Li.Automatic Registration of Terrestrial LiDAR Data Using Planar Targets[D].Zhengzhou:Information Engineering University,2010)
[3]王力,李广云,张启福,等 激光扫描中平面拟合及坐标转换模型构建[J].测绘科学技术学报,2011,29(2):101-104(Wang Li,Li Guangyun,Zhang Qifu,et al.Plane Fitting and Transformation in Laser Scanning[J].Journal of Geomatics Science and Technology,2011,29(2):101-104
[4]潘国荣,秦世伟,蔡润彬,等.三维激光扫描拟合平面自动提取算法[J].同济大学学报:自然科学版,2009,37(9):1 250-1 255(Pan Guorong,Qin Shiwei,Cai Runbin,et al.Fitted Plane Automatic Extraction Algorithm of 3D Laser Scanning[J].Journal of Tongji University:Natural Science,2009,37(9):1 250-1 255)
[5]Biosca J,Lerma J.Unsupervised Robust Planar Segmentation of Terrestrial Laser Scanner Point Clouds Based on Fuzzy Clustering Methods[J].ISPRS Journal of Photogrammetry and Remote Sensing,2008,63(1):84-98
[6]戴楠,李传荣,苏国中,等.激光点云提取建筑物平面目标算法研究[J].微计算机信息,2010,26(7):205-207(Dai Nan,Li Chuanrong,Su Guozhong,et al.Algorithms Study of Building Planar Objects Detection on LiDAR Data[J].Microcomputer Information,2010,26(7):205-207)
[7]李泽宇,李德华,胡汉平,等.基于八叉树的三维散乱数据点法矢的估计[J].计算机与数字工程,2000,28(4):62-65(Li Zeyu,Li Dehua,Hu Hanping,et al.Estimation of Normal Vector of 3DScattered Point Based on Octree[J].Computer &Digital Engineering,2000,28(4):62-65)
[8]鲁铁定,周世健,张立亭,等.基于整体最小二乘的地面激光扫描标靶球定位方法[J].大地测量与地球动力学,2009,29(4):102-105(Lu Tieding,Zhou Shijian,Zhang Liting,et al.Sphere Target Fixing of Point Cloud Data Based on TLS[J].Journal of Geodesy and Geodynamics,2009,29(4):102-105)
[9]官云兰,程效军,施贵刚.一种稳健的点云数据平面拟合方法[J].同 济 大 学 学 报:自 然 科 学 版,2008,36(7):981-984(Guan Yunlan,Cheng Xiaojun,Shi Guigang.A Robust Method for Fitting a Plane to Point Clouds[J].Journal of Tongji University:Natural Science,2008,36(7):981-984)
[10]官云兰,刘绍堂,周世健,等.基于整体最小二乘的稳健点云数据平面拟合[J].大地测量与地球动力学,2011,31(5):80-83(Guan Yunlan,Liu Shaotang,Zhou Shijian,et al.Robust Plane Fitting of Point Clouds Based on TLS[J].Journal of Geodesy and Geodynamics,2011,31(5):80-83)
[11]隋立芬,宋力杰.误差理论与测量平差基础[M].北京:解放军出版社,2004(Sui Lifen,Song Lijie.Error Theory and Base of Surveying Adjustment[M].Beijing:PLA Press,2004)
[12]杨凡,李广云,王力.三维坐标转换方法研究[J].测绘通报,2010(6):5-7(Yang Fan,Li Guangyun,Wang Li.Research on the Methods of Calculating 3DCoordinate Transformation Parameters[J].Bulletin of Survey and Mapping,2010(6):5-7)

