基于断裂力学的煤层气井破裂压力计算方法

东 振， 刘亚东， 鲍清英， 张 义， 陈姗姗

( 1. 中国石油勘探开发研究院 廊坊分院，河北 廊坊 065007； 2. 中国矿业大学 资源与地球科学学院，江苏 徐州 221008 )



基于断裂力学的煤层气井破裂压力计算方法

东 振1， 刘亚东2， 鲍清英1， 张 义1， 陈姗姗1

( 1. 中国石油勘探开发研究院 廊坊分院，河北 廊坊 065007； 2. 中国矿业大学 资源与地球科学学院，江苏 徐州 221008 )

为了提高煤层气井破裂压力预测精度，运用断裂力学理论推导裂缝性地层破裂压力计算公式，结合分形岩石力学理论建立裂缝性地层破裂压力解析模型，提出一种实用的破裂压力计算方法.结果表明：在非均匀地应力下，煤岩井壁更易沿最大水平主应力方向起裂，解析模型与传统模型在表达形式上具有统一性和更广泛的适用性.煤岩裂缝具有分形特征，分形效应提高岩石阻碍裂缝扩展的能力，当分形维数越大、相似比越小时破裂压力越大.在不同裂缝状态下，缝长对破裂压力的影响规律不同，当裂缝长度较小时破裂压力随裂缝长度增加而迅速减小；当裂缝长度增加到一定数值后，闭合裂缝破裂压力随缝长增加而增大，开启裂缝破裂压力随缝长增加而减小并趋于定值.郑庄地区5口煤层气井实例计算表明：该计算方法预测的破裂压力误差在10%以内，破裂压力对缝长变化特别敏感，合理确定裂缝长度对准确预测破裂压力尤为重要.

破裂压力； 断裂力学； 分形几何； 有限元； 煤层气

0 引言

煤岩中大量发育的自生割理，使得煤岩与砂泥岩在岩体结构上存在很大差异，岩石力学破裂压力计算模型没有考虑裂缝的影响，这种局限性使得岩石力学计算方法并不适用于裂缝性地层[1-2].由于没有针对煤层气井有效、实用的破裂压力计算方法，煤层气井破裂压力预测结果往往不能有效指导现场实践，准确地预测煤层破裂压力成为煤层气钻完井工程亟需解决的问题.

煤岩是裂隙—孔隙型双孔介质，考虑裂缝存在时破裂压力计算转变为断裂力学I型裂缝问题.Atkinson B K[3]将断裂力学运用于水力压裂，建立井壁裂纹扩展的断裂力学模型.Laubach S E等[4]对煤层裂缝进行断裂力学分析，认为裂缝上、下高点比裂缝走向端点应力集中程度更大，给出裂缝开裂时需满足的应力条件.在水平井井壁稳定模型的基础上，Ai C等[5]分析钻井液浸泡时间、井眼直径和裂缝长度对强度因子的影响.阳友奎[6]、卢国胜[7]等基于断裂力学模型推导应力强度因子和破裂压力，通过盐岩假三轴水力压裂实验对研究结果进行验证.曹光言等[8]应用断裂力学理论，建立不同完井方式下油气井破裂压力计算模型.唐书恒[9]、颜志丰[10]等运用有限元方法讨论地应力、裂缝方位对破裂压力影响.在破裂压力研究过程中，存在问题：(1)模型没有考虑地层压力；(2)在推导过程中没有考虑裂缝启闭状态；(3)没有考虑分形效应影响；(4)采用边界配置法计算近似解，需要查阅图版得到相关系数.

笔者运用有限元法讨论裂缝性地层井壁起裂位置，综合考虑地层压力、裂缝形态和分形效应，建立裂缝性地层破裂压力解析模型，为煤层气井破裂压力计算提供思路.

1 井壁起裂位置

1.1 单裂缝

井壁起裂位置是建立破裂压力计算模型时必须考虑的问题，在建立计算模型时，一般假设沿最大水平主应力方向的井壁最先发生破坏.采用Ansys有限元软件分析裂缝性井壁的起裂位置，假设条件：

(1)煤岩为横观各向同性的线弹性材料；

(2)不考虑温度、渗流与应力的耦合效应；

(3)裸眼完井，不考虑井眼扩径；

(4)模型为二维平面模型，模型尺寸相对井筒直径足够大，以消除边界效应影响；

(5)单裂缝由两条沿径向分布的等长对称矩形缝构成，考虑缝宽时为开启裂缝，忽略缝宽时为闭合裂缝(长宽比足够大时，可以将矩形缝视为线性缝).

闭合单裂缝模型(见图1(a))参数：二维平面模型(3 m×3 m)，模型左边界、下边界采用固定约束，最大水平主应力平行于x轴，最小水平主应力平行于y轴，井筒内载荷垂直于井壁，杨氏模量为7.51 GPa，泊松比为0.38，抗拉强度为1.19 MPa；采用2维、8节点结构实体单元(PLANE82)，三角形网格划分，模型外边界分60段，井筒内边界分120段，裂缝分5段，井筒半径为100 mm，单缝半长为5 mm，裂缝长宽比为20，裂缝与最大水平主应力间的夹角以10°为间隔从0°变化到90°.在计算过程中，井壁最大拉应力与井筒内载荷呈线性关系[11]，最大拉应力等于抗拉强度时井筒内载荷即为煤岩破裂压力.

图1 单裂缝和多裂缝有限元模型

不同地应力、裂缝角度下破裂压力见表1，其中σh1为最大水平主应力；σh2为最小水平主应力.由表1可以看出：

(1)裂缝沿最大水平主应力方向时破裂压力最小，沿最小水平主应力方向时破裂压力最大.

(2)最大水平主应力不变，破裂压力随最小水平主应力增大而增大；最小水平主应力不变，破裂压力随最大水平主应力增大而减小.

(3)采用岩石力学公式计算的破裂压力,大于裂缝沿最大水平主应力方向时破裂压力，但小于高角度裂缝时破裂压力.

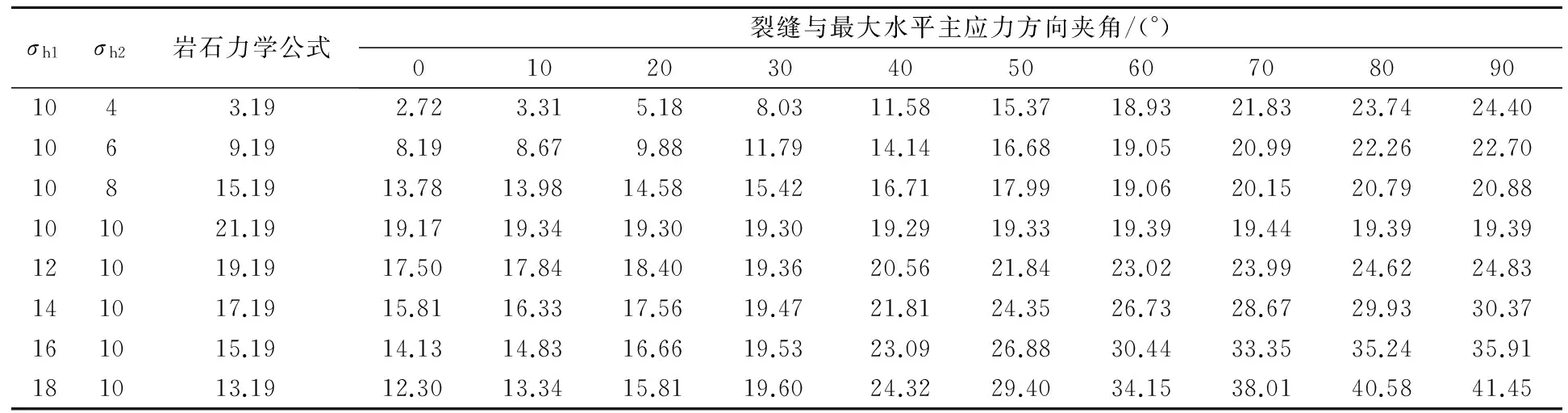
表1 不同地应力、裂缝角度下破裂压力Table 1 The fracture pressure under different in-situ stress and crack orientations MPa

1.2 多裂缝

不同方位裂缝共存时井壁更符合工程实际，因此对多裂缝共存的煤岩井壁进行有限元数值模拟.多裂缝模型(见图1，其中p为井筒压力)的井壁均布18条单裂缝，两条裂缝角度间隔10°，其中水平缝与最大水平主应力方向一致，考虑裂缝间相互影响和计算精度将裂缝分10段，其他模型参数、力学参数、裂缝几何参数与单裂缝模型的一致.有限元数值模拟结果表明：

(1)裂缝尖端应力与原始地应力关系密切，水平应力差越大，裂缝尖端的应力差异越明显.在非均匀地应力条件下，沿最大水平主应力方向裂缝尖端应力集中最为严重，是井壁上最先起裂的位置，井壁起裂后易形成单一裂缝(见图2(a)).

(2)在均匀地应力条件下，不同方位裂缝的尖端应力差异小，井壁起裂后易形成径向裂缝(见图2(b)).

图2 多裂缝尖端应力云图

2 破裂压力

割理是煤层中垂直层面分布的系统裂缝，常被方解石、黏土、黄铁矿等矿物及其他胶结物充填，根据充填程度分为完全充填割理、充填割理和未充填割理[12]；煤岩在填充物、应力(地应力和构造应力)共同作用下存在开启、闭合状态裂缝，在钻井过程中可以遇到.为方便建立模型，假设条件：

(1)只考虑沿最大水平主应力方向的径向裂缝；

(2)井壁周围不存在异常地层压力；

(3)不考虑井眼扩径和钻井液向地层的渗透作用.

考虑裂缝启闭状态和地层压力，建立裂缝性地层破裂压力计算模型(见图3)，其中po为地层压力；R为井筒半径;a为裂缝半长；x为裂缝上某点到井眼中心的距离.根据弹塑性力学[13]得到不考虑地层压力时周向应力表达式为

(1)

式中:σ(x)为距离井眼中心x处周向应力；θ为裂缝与最大水平主应力方向夹角，模型中裂缝与最大水平主应力方向一致，夹角为0°.根据断裂力学[14]无限板内半长为a的拉伸裂纹强度因子尖端应力计算公式，计算模型裂缝强度因子：

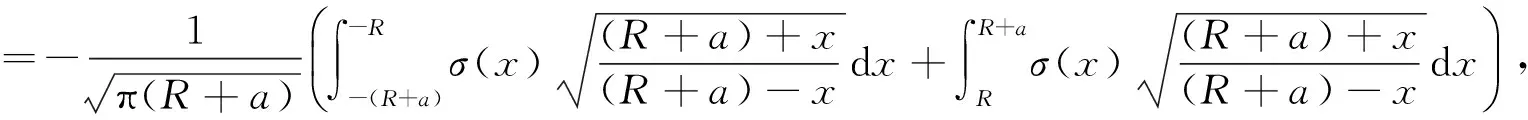
(2)

式中:KⅠ为Ⅰ型裂缝强度因子，以拉应力为正，以压应力为负.模型中裂缝受压应力，故式(2)变号.

2.1 闭合裂缝

计算强度因子是求解Ⅰ型裂缝问题的关键，由于裂缝的启闭状态影响裂缝上有效应力的分布，因此对不同状态下裂缝分别进行强度因子计算.对于闭合裂缝，裂缝与井筒不连通，因此裂缝内、外压力与地层压力相等，将作用在裂缝上的地应力、井筒压力和地层压力分别代入式(2)，积分后由叠加原理得到总强度因子；根据Ⅰ型裂缝起裂准则，建立强度因子与断裂韧性之间关系，进而推导闭合裂缝破裂压力.

图3 闭合、开启状态裂缝破裂压力计算模型

(1)沿最大水平主应力方向，距离井眼中心x处地应力作用下表达式为

(3)

将式(3)代入式(2)并积分，得到地应力作用下裂缝强度因子KⅠ1：

(4)

式中：σ1(x)为距离井眼中心x处地应力；l=1+a/R，a/R为裂缝半长与井眼半径之比，简称为缝径比；f(l)、g(l)为与缝径比有关的无量纲因数.

(2)井筒压力p在距离井眼中心x处产生的周向应力为-pR2/x2，将它代入式(2)并积分，得到井筒压力作用下裂缝强度因子KⅠ2：

(5)

式中：h(l)为与缝径比有关的无量纲因数.

(3)裂缝内、外受到地层压力作用，将-po代入式(2)并积分，得到地层压力作用下裂缝强度因子KⅠ3：

(6)

式中：q(l)为与缝径比有关的无量纲因数.

将式(4-6)进行叠加，根据Ⅰ型裂缝开裂准则，得到裂缝开裂要需满足应力条件为

(7)

式中：KⅠC为Ⅰ型裂缝的岩石断裂韧性.

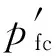
(8)

其中

式(8)等号两边量纲一致，符合量纲和谐原理，将等号右边第三项定义为名义抗拉强度；它与岩石的杨氏模量、泊松比、断裂能和缝径比等有关，可以作为不考虑外力作用时岩石抗拉强度；岩石断裂韧性实验表明断裂韧性与抗拉强度存在一定线性关系[15]，式(8)间接证明该观点.当裂缝长度值趋近于0时，地应力、地层压力前的应力因数极限值分别为3、1、1，应力因数极限值与岩石力学中破裂压力计算公式的因数一致.可以将均质砂泥岩地层作为裂缝性地层在裂缝长度值为0时的特殊情况，岩石力学破裂压力计算公式作为式(8)在裂缝长度值为0时的特殊表达式，因此式(8)具有更广泛的适用性.

2.2 开启裂缝

裂缝开启时裂缝与井筒连通，裂缝内压力等于井筒压力，裂缝外受地层压力作用，裂缝上作用垂直于裂缝的均布力(井筒压力与地层压力之差)，将作用在裂缝上的地应力、均布力分别代入式(2)并计算，利用叠加原理得到裂缝强度因子；根据Ⅰ型裂缝起裂准则，建立强度因子与断裂韧性之间关系，因推导过程较为繁琐，仅给出开启裂缝时破裂压力计算公式：

(9)

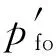
式(9)中应力因数、名义抗拉强度表达式与式(8)的不同，地层压力对破裂压力的影响不再与裂缝长度有关.当裂缝长度值趋近于0时，式(9)中最大主应力与最小主应力前的应力因数极限值分别为1、3，式(8)、式(9)中名义抗拉强度比的极限值等于1，即不存在裂缝时式(9)和式(8)计算的破裂压力相等，与实际情况相符.

3 公式修正

在公式推导过程中，将井壁周围裂缝作为线性缝处理，现场实测和实验观测表明，裂缝表面具有非线性、不规则的特点，岩石中裂缝不只沿直线扩展.岩石的断裂行为具有分形特征[16-18]，可以利用分形岩石力学理论对公式进行修正.分形理论的核心是“自相似性”，定量描述这种相似性的参数是分形维数，测井曲线可以连续记录不同深度地层的物性和裂缝发育情况，因此可以通过测井资料的变尺度分析计算裂缝分形维数.

变尺度分析法(R/S分析)是目前应用最广泛、最成熟的分形统计方法之一[19]，R称为极差，代表时间序列的复杂程度；S称为标准差，代表时间序列的平均趋势；R/S刻画无因次时间序列的相对波动强度.如果R(n)/S(n)与n在双对数坐标系下能回归出较好的线性关系，就代表该时间序列具有自相似性的分形特征.测井参数(声波时差、深浅电阻率和密度)R/S分析后得到的直线斜率H即为Hurst指数，分形维数D由2-H计算[20].对于一维过程Z(t)，R/S分析过程为

(10)

式中:n为分析层段测井采样点数；u为由端点开始在0～n之间依次增加的样点数；Z为随采样点变化的测井参数；i，j为样点数的变量；R(n)为测井参数全层段极差；S(n)为测井参数全层段标准差.

根据分形岩石力学理论，得到考虑分形效应后的岩石断裂韧性[21]为

(11)

式中:KⅠCD为沿分形裂缝断裂的岩石断裂韧性；E为杨氏模量；υ为泊松比；r为相似比；γs为线性扩展时单位宏观断裂面表面能.

将考虑分形效应的岩石断裂韧性代入式(8)和式(9)，得到修正后的破裂压力计算公式为

(12)

(13)

式中：pfc为修正后闭合裂缝破裂压力；pfo为修正后开启裂缝破裂压力.

4 实例分析

分析山西沁水盆地郑庄区块5口煤层气邻井.通过内压厚壁空心圆柱实验，鲜保安[22]得到山西永红煤矿的煤岩断裂韧性范围为0.13～0.24 MPa·m1/2，平均为0.22 MPa·m1/2；刘志强[23]通过实验获得郑庄区块煤岩的抗拉强度范围为0.42～1.56 MPa，平均为0.90 MPa；颜志丰等[10]通过实验获得沁南寺河煤矿的煤岩抗拉强度范围为0.68～1.34 MPa，平均为1.19 MPa.实例计算中取断裂韧性为0.22 MPa·m1/2，抗拉强度为1.19 MPa，杨氏模量为7 GPa，泊松比为0.31，井眼直径为215.9 mm.

4.1 地应力与地层压力

在郑庄区块地质模型基础上，开展基于多井约束优化的地应力数值模拟(见图4)，5口煤层气井最大水平主应力范围为24.88～25.66 MPa，最小水平主应力范围为14.27～14.91 MPa，距研究区最近的一口原地应力测试井的最大水平主应力为23.08 MPa，最小水平主应力为14.77 MPa，数值模拟结果与测试结果的相对误差较小(小于10%).郑庄区块实测与计算煤层压力的关系见图5.由图5可以看出，研究区注入/压降测试获得的煤层压力,与根据煤层深度计算的煤层压力间存在较好的线性关系，可以根据两者关系计算煤层压力，5口煤层气井的地应力和煤层压力计算结果见表2.

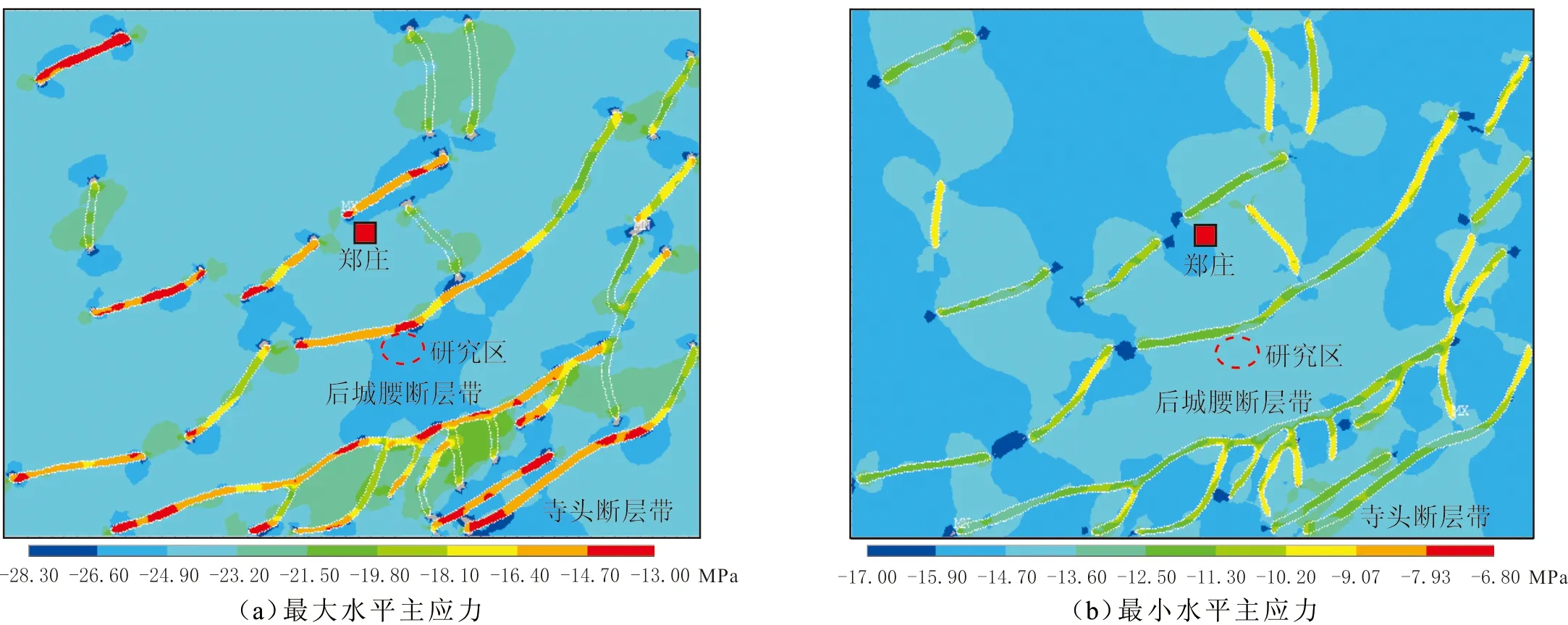
图4 沁水盆地郑庄区块地应力预测

4.2 分形参数

W2井煤层段测井资料变尺度分析曲线见图6.由图6可以看出，R/S曲线呈良好的线性关系，表明煤层裂缝具有分形特征.5口煤层气井分形维数计算结果见表3.由表3可以看出，W3井煤层段的分形维数比测井段的分形维数要小，说明煤层相对于砂泥岩地层裂缝欠发育.声波时差对于煤层孔渗变化有较强的响应，尤其是裂缝段被气体、液体充填时声波时差反应明显，并存在周波跳跃现象[24].由于声波时差R/S曲线的相关系数普遍较大，文中以声波时差R/S分析得到的分形维数为标准.深、浅双侧向电阻率的分形维数基本相同，与声波时差变尺度分析结果相比，测井段分形维数计算结果偏大.密度的变尺度分析结果与声波时差变尺度分析结果相近，但个别井相关因数偏小.孙丽凤[25]、李玮等[26]给出分形维数、相似比和

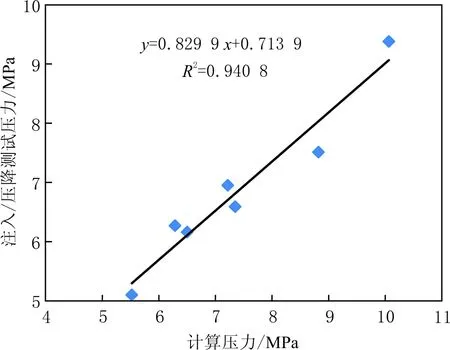
图5 沁水盆地郑庄区块实测与计算煤层压力的关系

弯折角之间数学关系，可以通过分形维数反算弯折角和相似比，计算结果见表2.

4.3 破裂压力预测结果

获得5口煤层气井地应力、煤层压力和分形参数后，通过小型压裂实验结果反算该井的缝径比为0.004，忽略煤岩割理裂缝变化影响，运用文中解析模型预测邻井破裂压力.由表2可以看出：由于传统模型没有考虑裂缝影响，解析模型与传统模型计算结果差距较大.解析模型比传统模型的预测精度提高，计算结果与实测破裂压力的相对误差在10%以内，误差产生原因：

(1)解析模型只考虑径向单裂缝，真实井眼周围发育不同方向和长度的裂缝系统，井壁不一定沿最大水平主应力方向起裂；

表2 建立解析模型与传统模型破裂压力计算结果Table 2 The fracture pressure calculation result of analytical model and traditional model

图6 W2井煤层段测井R/S分析曲线Fig.6 Coal seam logging data R/S Analysis of well W2

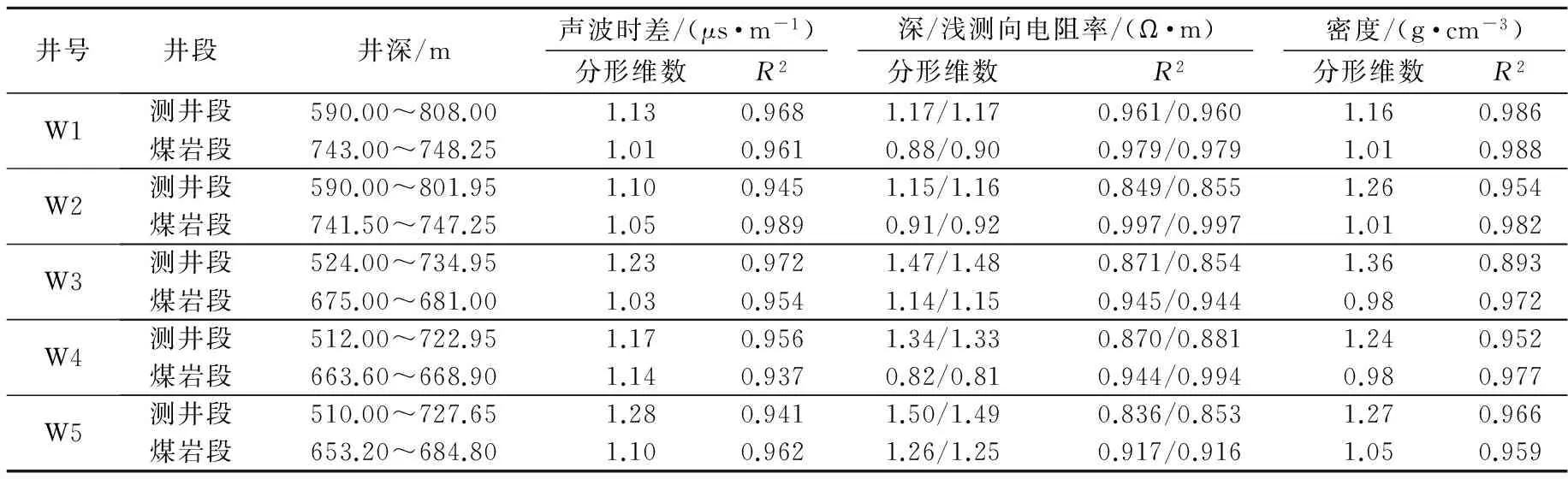
表3 5口煤层气井分形维数计算结果Table 3 The calculation result of fractal dimension

(2)每口井的裂缝发育不同，解析模型对地质条件稳定、煤岩性质变化小的地区预测效果好，在裂缝发育差异较大时误差较大.

4.4 破裂压力影响因素

缝径比与分形参数分别表征裂缝宏观和微观发育，是影响破裂压力的两个关键因素.缝径比对破裂压力的影响见图7.由图7可以看出：闭合裂缝破裂压力随缝径比增加先减小后增加；开启裂缝破裂压力随缝径比增加逐渐减小并趋于定值.短裂缝改变井筒周围的岩石结构，应力集中现象使得井壁岩石更易破坏，从而导致破裂压力降低.闭合裂缝尖端达到起裂条件前整个裂缝张开，随裂缝长度增加所需能量和破裂压力也随之增加.裂缝开启时受力与岩石力学中破裂压力计算模型类似，裂缝上只作用井筒压力、地应力和地层压力，地应力随裂缝长度增加而不断减小，并趋于最小水平主应力，破裂压力不断减小；当超过井筒附近的应力集中区(5～10倍井筒半径)后，裂缝尖端处的应力状态不再变化，破裂压力也趋于定值.

分形参数对破裂压力的影响见图8.分形维数表征裂缝的复杂程度，分形维数越大,说明裂缝扩展路径越不规则，扩展裂缝在产生更大断裂面积的同时也将消耗更多的表面能.相似比表征裂缝的最小分形尺寸，分形相似比越小，说明对裂缝分形程度的测量精度越高，分形裂缝测量长度也越大，因此裂缝扩展所需能量也越多.总之，分形效应提高岩石阻碍裂缝扩展的能力，增加破裂压力.

图7 缝径比对破裂压力的影响

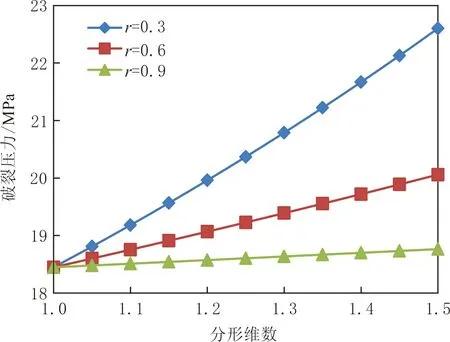
图8 分形参数对破裂压力的影响

5 结论

(1)建立的解析模型与岩石力学模型在表达形式上具有统一性和更广泛的适用性，岩石力学模型可以作为解析模型在缝长值为0时的特殊情况，解析模型的破裂压力计算公式间接证明岩石断裂韧性与抗拉强度之间存在线性关系.

(2)裂缝在开启、闭合时应力状态不同，缝长对破裂压力的影响规律不同.煤层裂缝具有分形特征，分形效应提高岩石阻碍裂缝扩展的能力，导致破裂压力增大.

(3)建立的解析模型具有较好的预测精度.在割理裂缝很小时，破裂压力对缝长变化特别敏感，合理选择裂缝长度对于准确预测煤层破裂压力尤为重要.

[1] 梁大川,蒲晓林,徐兴华.煤层坍塌的特殊性及钻井液对策[J].西南石油学院学报,2002,24(6):28-31. Liang Dachuan, Pu Xiaolin, Xu Xinghua. Particularity of coal collapse and drilling fluid countermeasure [J]. Journal of Southwest Petroleum Institute, 2002,24(6):28-31.

[2] 沈海超,程远方,赵益忠,等.靖边气田煤层地应力及井壁稳定研究[J].岩石力学,2009,30(S2):123-126. Shen Haichao, Cheng Yuanfang, Zhao Yizhong, et al. Research on in-situ stresses and borehole stability of coal seam in Jingbian gas field [J]. Rock and Soil Mechanics, 2009,30(Supp.2):123-126.

[3] Atkinson B K. Fracture mechanics of rock [M]. London: Academic Press Limited,1987:231-255.

[4] Laubach S E, Marrett R A, Olson J E, et al. Characteristics and origins of coal cleat: A review [J]. International Journal of Coal Geology,1998,35(1-4):175-207.

[5] Ai C, Hu C , Zhang Y, et al. Wellbore stability estimation model of horizontal well in cleat-featured coal seam [C]. SPE 167767,2014.

[6] 阳友奎,周时光.地层水力压裂中的应力强度因子[J].四川建材学院学报，1993,8(3):39-45. Yang Youkui, Zhou Shiguang. The stress intensity factors for hydraulic fracturing in rock formation [J]. Journal of Sichuan Institute of Building Material，1993,8(3):39-45.

[7] 卢国胜,张家达,阳友奎.水力压裂破裂压力的导出及实验验证[J].中国矿业，1988,7(4):42-44. Lu Guosheng, Zhang Jiada, Yang Youkui. Breakdown pressure formula deduced and proved experimentally under hydraulic fracturing [J]. China Mining Magazine, 1988,7(4):42-44.

[8] 曹言光,刘长松,林平,等.应用断裂力学理论建立油气井压裂时岩石破裂压力计算模型[J].西安石油学院学报:自然科学版,2003,18(4):36-39. Cao Yanguang, Liu Changsong, Lin Ping, et al. Establishing the models for calculating the fracturing pressure of formation rock during oil/ gas wells fracturing by using fracture mechanics theory [J]. Journal of Xi'an Petroleum Institute: Natural Science Edition, 2003,18(4):36-39.

[9] 唐书恒,朱宝存,颜志丰.地应力对煤层气井水力压裂裂缝发育的影响[J].煤炭学报,2011,36(1):65-69. Tang Shuheng, Zhu Baocun, Yan Zhifeng. Effect of crustal stress on hydraulic fracturing in coalbed methane wells [J]. Journal of China Coal Society, 2011,36(1):65-69.

[10] 颜志丰,琚宜文,唐书恒.沁水盆地南部煤层气储层压裂过程数值模拟研究[J].地球物理学报,2013,56(5):1734-1744. Yan Zhifeng, Ju Yiwen, Tang Shuheng, et al. Numerical simulation study of fracturing process in coalbed mechanic reservoirs in southern Qinshui basin [J]. China Journal of Geophysics, 2013,56(5):1734-1744.

[11] 朱宝存,唐书恒,颜志丰,等.地应力与天然裂缝对煤储层破裂压力的影响[J].煤炭学报,2009,34(9):1199-1202. Zhu Baocun, Tang Shuheng, Yan Zhifeng, et al. Effects of crustal stresses and natural fractures on fracture pressure of coal reservoirs [J]. Journal of China Coal Society, 2009,34(9):1199-1202.

[12] 张胜利.煤层割理及其在煤层气勘探开发中的意义[J].煤田地质与勘探,1995,23(4):27-31. Zhang Shengli. Cleat and its significance in the exploration and development of coalbed methane [J]. Coal Geology & Exploration, 1995,23(4):27-31.

[13] 徐芝伦.弹性力学[M].北京:高等教育出版社,1978:55-58. Xu Zhilun. Elastic mechanic [M]. Beijing: Higher Education Press, 1978:55-58.

[14] 程靳,赵树山.断裂力学[M].北京:科学出版社,2006. Cheng Jin, Zhao Shushan. Fracture mechanics [M]. Beijing: Science Press, 2006.

[15] 满轲,周宏伟.不同赋存深度岩石的动态断裂韧性与拉伸强度研究[J]. 岩石力学与工程学报,2010,29(8):1657-1663. Man Ke, Zhou Hongwei. Research on dynamic fracture toughness and tensile strength of rock at different depths [J]. Chinese Journal of Rock Mechanics and Engineering, 2010,29(8):1657-1663.

[16] 闫铁,李玮.分形岩石力学在油气井工程中的应用[J].大庆石油学院学报,2010,34(5):60-64. Yan Tie, Li Wei. Application of fractal rock mechanics to oil and gas engineering [J]. Journal of Daqing Petroleum Institute, 2010,34(5):60-64.

[17] 谢和平.分形几何及其在岩土工程中的应用[J].岩土工程学报,1992,14(1):14-24. Xie Heping. Fractal geometry and its application to rock and soil materials [J]. Chinese Journal of Geotechnical Engineering, 1992,14(1):14-24.

[18] 王有智,王世辉.鹤岗煤田构造煤孔隙分形特征[J].东北石油大学学报,2014,38(5):61-66. Wang Youzhi, Wang Shihui. Fractal characteristics of tectonic coal from Hegang coal field [J]. Journal of Northeast Petroleum University, 2014,38(5):61-66.

[19] 杨红梅,王继伟,藏晓华,等.变尺度分形技术在西峰油田白马中区裂缝预测中的应用[J].科学技术与工程,2012,12(33):8826-8831. Yang Hongmei, Wang Jiwei, Zang Xiaohua, et al. Application of variable scale fractal technique for bearkthrough forecast in the middle part of Baima, Xifeng oilfield [J]. Science Technology and Engineering, 2012,12(33):8826-8831.

[20] Pang J, North C P. Fractals and their applicability in geological wireline log analysis [J]. Journal of Petroleum Geology, 1996,19(3):339-350.

[21] 张杨,袁学芳,闫铁,等.水力裂缝分形扩展对压裂效果的影响[J].石油钻探技术,2013,41(4):101-104. Zhang Yang, Yuan Xuefang, Yan Tie, et al. Influence of hydraulic fracture fractal propagation on fracturing result [J]. Petroleum Drilling Techniques, 2013,41(4):101-104.

[22] 鲜保安.煤层气田多分支水平井优化设计研究[D].北京:中国石油大学(北京),2006. Xian Baoan. Research on optimization design of multi-lateral well for coalbed methane field [D]. Beijing: China University of Petroleum(Beijing), 2006.

[23] 刘志强.煤层气地应力预测方法研究——以郑庄煤层气区块为例[D].北京:中国地质大学(北京),2014. Liu Zhiqiang. Method of estimating in-situ stresses: A case study of Zhengzhuang coalbed methane field [D]. Beijing: China University of Geosciences(Beijing), 2014.

[24] 王理瑞,赵国春,王国先,等.用R/S分析技术预测火烧山油田H2层油藏裂缝[J].新疆石油地质,2011,32(4):415-417. Wang Lirui, Zhao Guochun, Wang Guoxian, et al. Application ofR/Sanalysis to fractural prediction in H2 reservoir in Huoshaoshan field [J]. Xinjiang Petroleum Geology, 2011,32(4):415-417.

[25] 孙丽凤.分形几何方法模拟混凝土材料的裂纹扩展[J].青岛建筑工程学院学报,1998,19(2):5-7. Sun Lifeng. A fractal kinked model for simulation of cracks development of reinforced concrete material [J]. Journal of Qingdao Institute of Architecture and Engineering, 1998,19(2):5-7.

[26] 李玮,闫铁,毕雪亮.水力致裂法测定分形裂纹下岩石的断裂韧性[J].岩石力学与工程学报,2009,28(1):2789-2793. Li Wei, Yan Tie, Bi Xueliang. Fracture toughness measurement of rock with fractal cracks using hydraulic fracturing [J]. Chinese Journal of Rock Mechanics and Engineering, 2009,28(1):2789-2793.

2015-10-08；编辑：任志平

国家科技重大专项(2011ZX05033，2011ZX05033-001，2011ZX05043-006)

东 振(1988-)，男，硕士，助理工程师，主要从事煤层气钻完井方面的研究.

P618.13

A

2095-4107(2015)06-0111-09

DOI 10.3969/j.issn.2095-4107.2015.06.013