扰动强度递增斜坡动力学演变规律的振动台试验

郭海强，姚令侃，2，3，黄艺丹，郭沉稳

（1.西南交通大学 土木工程学院，四川 成都 610031；2.西南交通大学 高速铁路线路工程教育部重点试验室，四川 成都 610031；3.西南交通大学 道路与铁道工程抗震技术研究所 抗震工程技术四川省重点试验室，四川 成都 610031）

1 引言

“5.12”汶川大地震是有现代观测仪器以来人类所记录到的地震触发崩塌滑坡灾害最严重的大地震，地震触发崩塌滑坡规模大小的分布规律成为地震次生灾害研究的基本科学问题之一。汶川地震后，通过对G213线都江堰至映秀段沿线公路边坡的现场调查，发现Ⅸ度地震烈度区崩塌滑坡方量与出现频率之间存在着负幂律关系，即令崩塌滑坡体方量为Q，方量大于Q 的工点数为N(Q)，获得Q 与N(Q)之间的关系式为：lgN(Q)=2.348-0.483lg(Q)，相关系数R2=0.96。

对于Ⅹ度区、Ⅺ度区，利用卫星遥感影像资料对崩塌滑坡的面积进行解译。受资料精度要求限制，选取了北川、安县、茂县和绵竹境内，及都江堰、彭州境内的两片区域。共判译出Ⅹ度区崩塌滑坡2 812处，Ⅺ度区崩塌滑坡3 159处。令崩塌滑坡面积（投影面积）为A，面积大于A 的崩塌滑坡数量为N(A)，分析崩塌滑坡面积与出现频率之间的关系。统计结果表明，在Ⅹ度区，地震触发的崩塌滑坡面积与出现频率的负幂律关系减弱，相关系数下降到0.91；Ⅺ度区，地震触发的崩塌滑坡面积与出现频率之间的关系服从对数正态分布，但其负幂律性质仍未完全消失，相关系数R2=0.87。

“4.20”芦山地震后，通过航片影像资料，对地震触发的崩塌滑坡进行解译。航片覆盖邛崃、荥经、名山、雨城、芦山、天全和宝兴等地的部分区域，研究区覆盖Ⅸ度、Ⅷ度以及部分Ⅶ度区。芦山地震判译出共发生1 701处崩塌滑坡，其中崩塌滑坡投影面积大于5×104m2的有6处（0.35%），104～5×104m2有56处（3.29%），103～104m2有657处（38.62%），小于103m2有982处（57.73%）。芦山地震最大地震烈度达Ⅸ度，面积约208 km2，共判译出近480处崩塌滑坡，其中最大的滑坡约12×104m3（见图1）。获得崩塌滑坡面积A 与面积大于A 的数量N(A)之间的关系式为：lgN(A)=4.16-0.678A，相关系数R2=0.90。

图1 双石-灵关公路上的滑坡Fig.1 A landslide at the road from Shuangshi to Lingguan

综上所述，笔者发现，随地震烈度增加，地震触发崩塌滑坡规模分布规律会发生变化。如在Ⅸ度地震烈度区，汶川地震和芦山地震的实震统计资料均凸现出地震崩塌滑坡方量（面积）与出现频率之间呈现负幂律分布；而在Ⅹ度区，汶川实震资料显示，地震触发山地灾害规模仍然服从幂律分布，但其幂律关系明显减弱；Ⅺ度区，这一关系服从对数正态分布。若超越这些从统计层面获得的表观认知，能否从理论上判断随地震强度增加，斜坡系统动力学特性演化是必然趋势？这是亟待从物理视角进行诠释的深层次科学问题。地震触发崩塌滑坡规模与发生频率的关系属于斜坡系统的总体特征，不取决于坡体失稳的微观机制，因此，不能通过分别分析个体灾点去了解其总体特征。

自组织临界状态（self-organized criticality，简称SOC）理论是Per Bak首先提出的新概念，用以解释复杂系统的行为特性。这类系统包含着众多的发生短程相互作用的组元，并自发地向着一种临界状态进化。在临界状态下即使是受到一系列微小的、均匀的扰动，其反应随时间的变化也很大，但每次扰动下表征反应规模的物理量可用幂律描述，故幂律可以作为判别SOC的证据。目前SOC是使整体理论适用于动态系统的惟一模型或数学描述[1－3]。研究SOC的主要方法包括物理砂堆模型试验和元胞自动机数值模拟[4－8]。

在地球物理学领域，我国於崇文[9]院士以完整和独立的命题提出了固体地球系统的复杂性与自组织临界性，认为，地质系统是自然界之中的一种异常复杂的开放、远离平衡、相互作用的巨大耗散动力系统。它具有自组织临界性的内禀基本属性，它的时空行为服从地质作用的自组织临界过程动力学。笔者认为，斜坡系统作为地质系统的子集，同样具有自组织临界性。砂堆模型反映了这种在自组织作用下的斜坡物质能量耗散普适性过程[10]。因此，期望在SOC的概念框架下，通过动力扰动的砂堆模型试验，从整体理论上研究随扰动强度递增斜坡动力学演变规律。

2 振动台砂堆模型试验

砂堆模型是自组织临界状态的经典范例，Held等[4]在IBM公司沃森研究中心设计完成了经典的砂堆模型试验。在试验过程中，通过改变漏斗的倾角和电机的转速，将设备调节到每隔15 s向直径为2 cm的圆盘中心掉落质量均匀的一粒砂，并且通过底部的高精度天平来测量滚出砂堆的砂粒质量，从一粒砂到数百粒砂不等。结果有力地表明，砂堆确实是自组织临界状态。此后，近20年来，世界各国研究人员采用砂粒或计算机程序模拟相继开展了各种类型的砂堆模型试验，并力图据此解释一些显示自组织临界状态的物理系统的机制。Somfai等[11]通过水侵蚀砂堆模型试验，研究了滑坡服从幂律分布问题；Katz等[12]通过使用长、高均为28 cm的正弦波振动箱砂堆模型试验，研究了振动作用下斜坡失稳的控制因素以及滑坡与振动频率大小的关系；杨庆华等[13]通过变动砂堆底坡的离心模型试验，基于拟静力法原理研究地震触发的崩塌滑坡，发现斜坡堆积体（按照重力相似准则高度达20.4 m）在砂堆模型底板倾斜1.5°内，斜坡堆积体崩塌的动力学特性可以用幂律描述。为更真实地体现斜坡在地震动力扰动作用下的动力学行为，本文开展了振动台砂堆模型试验，希望能够在SOC的概念框架下，从物理角度对随扰动强度递增斜坡的动力学演变规律进行诠释，探讨不同地震强度作用下斜坡失稳具普适性的分布概型。

2.1 试验设计

试验的目的是关注随地震强度的增加，斜坡体静平衡破坏时的宏观效应，这种宏观效应可用滑落出砂堆砂粒的重度度量。地震触发崩坍滑坡是规模差异巨大的自然现象（几～几亿立方米），而且没有特征尺度，所以在砂堆模型设计时并不强调对原型工点尺度的相似关系。已有砂堆试验的研究表明，模型材料的级配、物理力学参数、模型大小等会对落砂量数值产生影响，但不会影响到落砂量规模与发生频率的关系。为较真实地反映汶川震区崩塌滑坡实际情况，选择G213线都江堰至映秀段典型地震触发崩塌工点，现场取土样，去除粒径大于50 mm的颗粒后测定级配（见图2）。向振动台台面加砂，当砂堆坡脚触及台面边缘并且达到天然休止角时砂堆达到临界状态，如图3所示。该砂堆总重量达6.8 t，长、宽、高分别为258、150、195 cm。

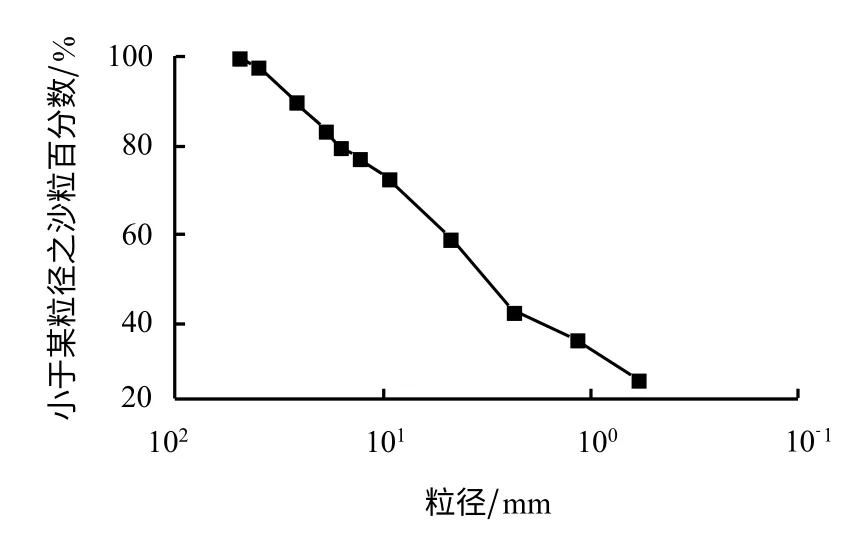
图2 试验砂粒级配曲线Fig.2 Gradation curve of sand sample

图3 砂堆模型Fig.3 Sandpile model

试验输入的是汶川地震卧龙台站记录的修正波，如图4所示。设计了地震波峰值加速度（PGA）从0.075g（g为重力加速度）开始至0.450g 的6组试验。以称重的方法测量每次地震波扰动后的落砂量，用近景摄影测量技术记录砂堆表面动力学过程。试验具体装置如图5所示。由于输入地震波的加速度是精确可控的，故可以重点研究随振动强度的增加，砂堆模型动力学特性的变化规律。

图4 汶川地震卧龙台站记录修正波Fig.4 Modified Wenchuan acceleration recorded by Wolongtai station

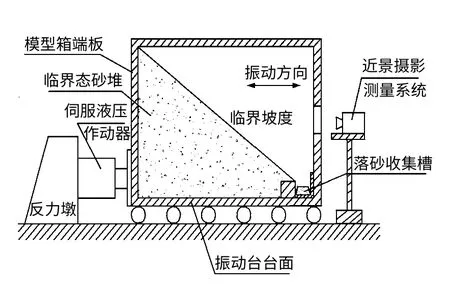
图5 振动台砂堆模型试验装置图Fig.5 Setup of the shaking table test

3 试验现象及统计分析

3.1 试验现象

（1）在试验中输入PGA为0.075g～0.125g 的地震波时，砂堆表面颗粒只在加速度峰值时段会发生点源（一处或几处分散在坡面的孤立颗粒）启动，其他时段，无颗粒启动现象。颗粒启动后基本可归纳为如下3类运动状态：①无砂粒滑出边界，即砂堆表面有少量颗粒发生滚动但未能滚落出边界；②有少量砂粒滑出边界，处在坡面上部的颗粒启动后，被下部的大颗粒阻挡，不但未发生连锁反应，自身也难以滑出边界，而在处于下部的颗粒较容易滑出边界，但行程短，缺乏带动效应；③大规模砂崩，砂堆表面上少数颗粒先启动，并带动其他颗粒，迅速扩大规模，使一定范围内的颗粒发生失稳，最终演变成一次大规模的砂崩。形成大小和深度都不同的“槽道”。由图6(a)可知，即使是大规模的砂崩，都只是发生在砂堆上的浅表层运动过程。该阶段发生大规模砂崩的影响范围有限，影响方式类似于多米诺骨牌效应。上述3种情形交叉出现，状态①、②出现较多，③相对较少。

图6 砂粒流通槽道Fig.6 Channel for sand flow

（2）在输入PGA为0.15g～0.25g 的地震波时，砂堆表面颗粒在加速度峰值点发生点源启动和局部面源（集聚在一块区域内的颗粒）启动。局部面源启动体现了颗粒群在地震波作用下同时运动的效应，而非颗粒相互作用。其他时段，砂堆表面颗粒只发生多点源启动，颗粒启动后的运动状态与现象1所描述的3种状态基本相同，主要以②、③两种状态为主，且出现砂堆表面“槽道”变多、变宽的现象，如图6(b)所示。

（3）在输入PGA为0.35g～0.45g 的地震波时，砂堆在加速度峰值出现时段内发生面层（模型坡面表层物质）启动。其他时段，还会发生点源启动现象，颗粒启动后的运动状态与现象（1）所描述的3种状态基本一致。该阶段砂堆表面上颗粒间的作用最剧烈，如图6(c)所示，砂堆上颗粒滚落的痕迹清晰可见，颗粒运动路径已经布满整个表面。原有的“槽道”变宽并扩展成整个砂堆表面。

3.2 试验数据统计分析

对试验结果进行统计分析，其统计特征值如表1所示。

通过分析振动台砂堆模型试验的统计结果，发现随着PGA的增加，样本均值随之增大，变异系数逐渐减小。样本检验结果共可分为3个阶段：①输入PGA为0.075g～0.125g 的汶川波时，小规模的落砂量次数显著多于大规模的落砂量。以第2组试验为例，在150次试验中高于600 g落砂量的只出现2次，而落砂量为0 g的却多达32次（由于0不能取对数，故在对崩塌次数与累计频率取双对数时，需要去除落砂量为0 g的数据）。数据结果具有很好的线性关系，如图7(a)所示，经检验服从幂律分布。②PGA增加到0.15g～0.25g 时，没有落砂量为0 g的数据出现，落砂量集中的峰值向右偏移。以第3组试验为例，由图7(b)可见，首尾部分线性关系减弱，落砂量与发生频率的幂律现象弱化，曲线呈3段式，区间2的线性关系很好，其斜率k2近似于拟合直线斜率，仍符合负幂率关系；区间1的曲线段斜率|k1|＜|k2|，表明，第3组试验小规模落砂事件偏少；区间3的曲线段斜率|k3|＞|k2|，表明，第3组试验大规模的砂崩事件比例增多。如图8(a)直方图所示，该阶段已发展成为具有衰减型尾部分布的曲线特征，经检验服从对数正态分布。③PGA增加到0.35g～0.45g 时，样本经检验服从正态分布。以第6组试验为例，由图8(b)PGA为0.45g 的直方图可知，该阶段样本已经具有正态分布的曲线特征，尽管峰值左偏，但与图8(a)PGA为0.15g 的直方图相比峰值已有明显右移。

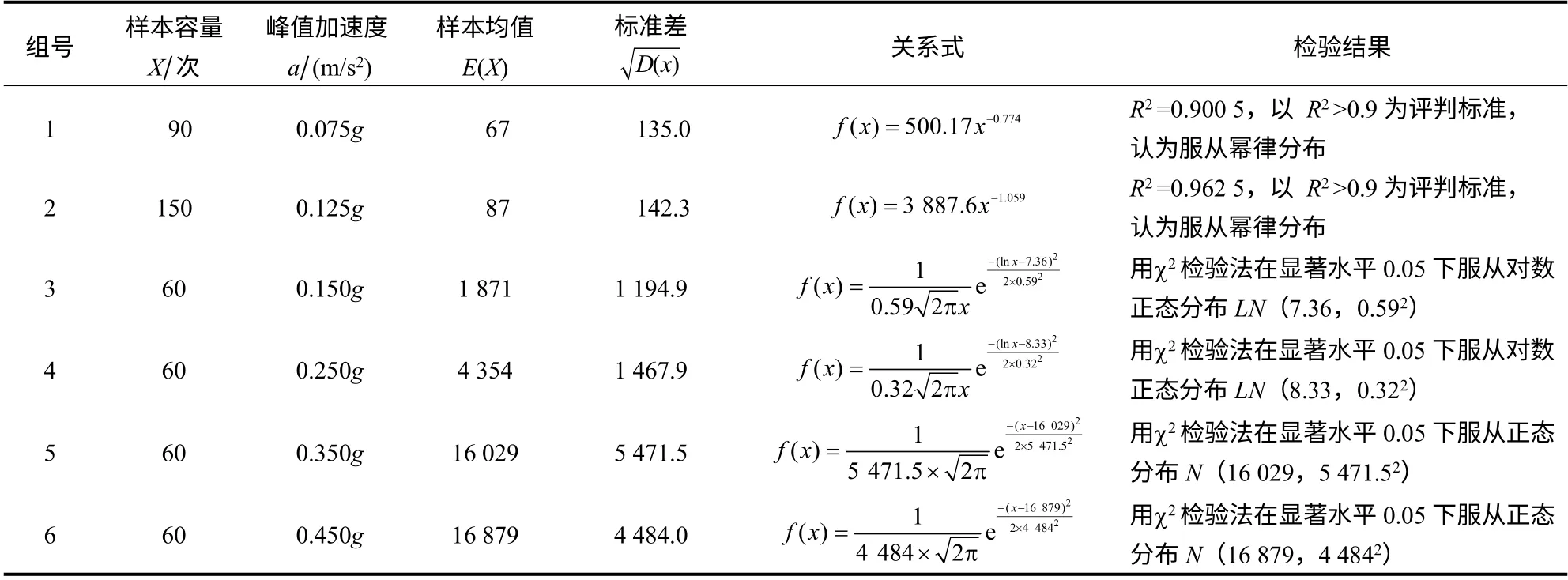
表1 试验结果统计表Table 1 A statistical table for the results of sandpile

图7 落砂量与累计频率双对数图Fig.7 Log-log plots of the avalanche amount and cumulative frequency

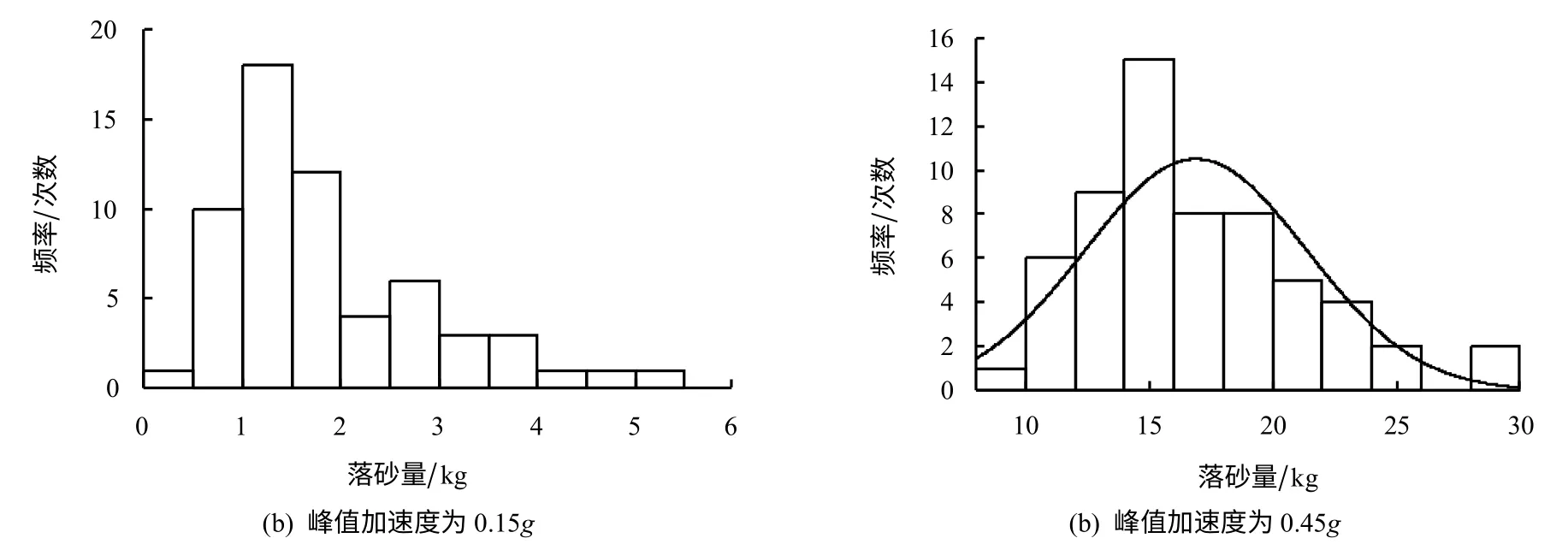
图8 落砂量直方图Fig.8 Histograms of avalanche amount

4 随振动强度增加砂堆动力学特性演变机制的元胞自动机模拟

振动台开展的砂堆模型试验结果表明，随着PGA的逐渐递增，砂堆模型塌滑规模与发生频率的关系经历了幂律—对数正态分布—正态分布的演变过程。在SOC研究领域，砂堆模型试验是贴近于原型现象的物理模拟，而元胞自动机数值模拟是获得SOC性质的主要途径[1]。本节将在自组织临界性的概念框架下，利用元胞自动机模拟手段，对不同强度扰动下砂堆模型动力特性的演变机制进行诠释。

针对振动台砂堆在地震波作用下坡面整体受到扰动且传播过程遵循物质守恒的特点，在设计元胞自动机模型时，扰动采用每一个元胞都增加一个定值的方式，扰动向相邻元胞的传播遵循能量守恒原则，具体为，以大小为L×L 的二维网格作为砂堆模型的边界范围，每个网格处存在一个元胞，用(i，j)代表元胞所处的位置（其中1≤i，j≤L），Fi，j为元胞(i，j)处的砂粒数值，在参数选择上，采用归一化的处理方式计数，Fi，j取0～1之间的数值，令阈值为1，L=50，采用Von Neumann型邻居方案，每个元胞有上、下、左、右4个邻居，在模型长度和宽度方向均考虑开放性边界条件[14]。

（1）生成砂堆：地震发生时，会同源引发该地区多处发生崩塌滑坡。为研究其整体分布规律，模型一次性生成N 个砂堆。每个砂堆规模相同，但初始状态不同。初始状态时，在各个砂堆中的任一元胞都会获得0～1之间随机选取的数值。

（2）砂堆演化到临界态：对每个砂堆而言，首先应找到该砂堆中所有元胞的最大值Fmax。其次，使砂堆中每一个元胞的值都增加1-Fmax（相当于对整个系统的一次扰动），对于任意元胞，如果Fi，j≥1，

则该元胞处于不稳定状态，必须向周边邻居发生倒塌，相互作用规则为

倒塌持续至所有元胞稳定（Fi，j﹤1）为止，由于模型是开放性的边界条件，故可能会有砂粒落出边界。当加入砂粒的数量与落在系统外的砂粒数量在总体达到平衡时，砂堆就停止增长。系统在这时达到临界状态。通过以上步骤，产生N 个处于临界状态，且每一元胞取值随机分配的砂堆。

（3）同时向N 个砂堆施加一次扰动，扰动强度为F′，每个砂堆的元胞值都统一增加F′，即Fi，j→Fi，j＋F′。元胞之间的相互作用仍按照上述规则执行。将记录落出系统外的砂粒数目作为每个砂堆落砂量的度量，对该组试验N 个砂堆的落砂量进行统计。

（4）改变扰动强度F′，重复步骤（3），获得砂堆在不同扰动强度下落砂量与发生频率的关系。

试验生成106个砂堆（N=106），先连续反应105次（均取F′=1-Fmax），以确保砂堆演化到临界状态。以扰动强度F′递增来模拟地震峰值加速度的增加，F′从0.001递增到0.040。令砂堆落砂量为S，落砂量等于S 的频率为p(S)，部分试验结果如表2所示。

表2 元胞自动机模拟试验结果统计Table 2 Results of cellular automata simulation

元胞自动机模拟试验结果表明，随扰动强度F′的增加，砂堆模型的动力特性经历了幂律—幂律弱化—正态分布的变化，而且这一演变过程是渐变的（见图9）。第1组试验时，F′=0.001，相当于加砂总数为2.5，属于微扰量级的传统砂堆模型。扰动结束后所有砂盘内砂粒总数平均为1 559，落砂量呈现幂律分布，其衰减的尾部是系统自组织效应的体现。此外，SOC系统是一个稳健的系统，即无论发生多大规模的雪崩，都不会使系统显著偏离临界态，在元胞自动机中，砂盘中的砂粒数总是在达到临界态时砂粒的数量附近波动。

第2组试验时，F′=0.008，相当于加砂总数为20，扰动强度虽然已超过微扰量级，但强制力尚未占据控制地位，这时，由强制力所决定的落砂量成分已经有所体现，但由系统自组织作用决定的随机性尚未被完全掩盖，表现为落砂量呈现为一种具有衰减型尾部的分布概型，本例中为Gamma分布。

第3组试验时，F′=0.040，相当于加砂总数为100，扰动量级远超过微扰量级。扰动结束后所有砂盘内砂粒总数平均为1 547，落砂量呈现正态分布。按照元胞自动机的模拟规则，砂盘内的砂粒容量是有限的，不会随加砂量的变化而变化。超过容量的加砂量只有落出砂盘。试验中加砂量是100，落砂量的均值也是100，构成落砂量概率分布的主体部分，可认为是强制力作用下系统的反应。由于砂盘的容量是具有一定弹性的，如图10所示，服从正态分布。这就是导致第3组试验中落砂量波动服从正态分布的主要因素。

此外，若在每次扰动后，若不仅统计落出系统外的砂粒量，而且还要加上砂盘内波动的砂粒数，则第2组试验中反映崩塌规模与发生频率的概率密度曲线用对数正态分布描述更为合理。

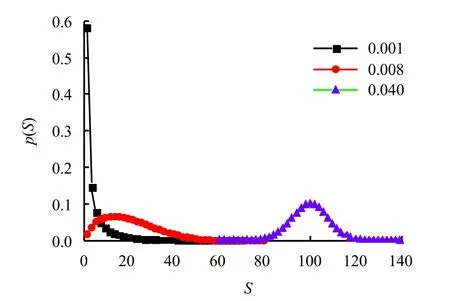
图9 不同扰动强度下崩塌规模的概率密度曲线Fig.9 Probability density curves of landslide scale under different disturbance intensities

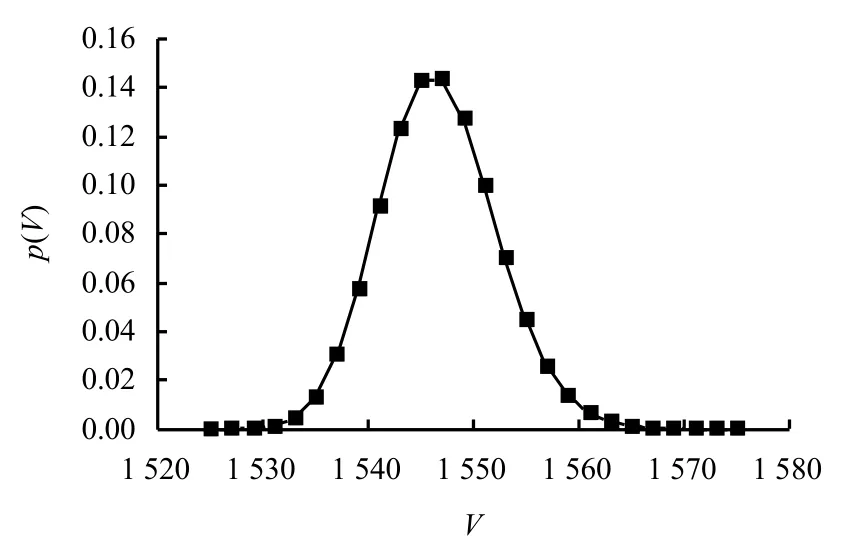
图10 F'=0.04时砂盘容量V 的概率密度曲线Fig.10 Probability density curve of V at F'=0.04

5 结论

（1）振动台砂堆模型试验结果表明，输入PGA为0.075g～0.125g 的汶川波时，落砂量与发生频率服从幂律分布；PGA增加到0.15g～0.25g 时落砂量服从对数正态分布；PGA增加到0.35g～0.45g 时，该阶段样本表现为具有正态分布的曲线特征。元胞自动机模拟试验结果表明，随扰动强度F′的增加，砂堆模型的动力特性同样也经历了幂律—幂律弱化—正态分布的演变过程。幂律弱化的标志是落砂量的分布虽不再服从幂律，但仍保持了具有衰减型尾部的特征。

（2）按照物理学中的普适性原理，汶川地震、芦山地震，在Ⅸ度区，地震崩塌滑坡规模与出现频率之间的负幂律关系，以及汶川地震Ⅺ度区地震触发崩塌滑坡面积的对数正态分布关系，可能是具普适性意义的概型；Ⅹ度区的统计关系说明，这种演变是渐进的。更进一步，虽然目前尚未获得Ⅻ度区的实震资料，但从振动台砂堆模型试验（PGA=0.35g～0.45g）、以及元胞自动机数值模拟（F′=0.04）落砂量统计结果，可以预测在Ⅻ度区应具有向正态分布发展的趋势。地震地质灾害分布受断层、地形地貌、岩性3大因素的控制[15－16]，上述结论主要反映的是地震烈度对崩塌滑坡分布规律的作用效应，在自然条件相近的区域，可以为高烈度地震山区地震触发崩塌滑坡灾势预测提供具有物理理论依据的概型，从而为开展地震触发山地灾害危险性区划、地震次生灾害风险评估等工作提供科学依据。

（3）SOC是1987年作为非平衡态统计力学的一个分支建立起来的，从那时起，对它的现象学研究和对它进行严谨的定义研究仍在进行。SOC已经使人们意识到阈值、亚稳定性、还有大规模波动在一大类多体系统的时空行为中起了决定性的作用，但扰动对SOC系统的影响是一直被忽视的。笔者先后完成了静水压力下的倾斜平面半无限松散砂堆边坡坍塌水箱试验、动水压力下的水槽砂堆模型试验、通过顶部加砂的无水单面坡干砂试验、通过变动砂堆底坡的离心机砂堆模型试验等[13，17－19]，以振动波为扰动源的砂堆模型系首次开展的工作。纵观上述各类试验，发现扰动方式不会对砂堆模型动力学基本特性产生显著影响，只会改变幂律关系式的参数；而扰动强度变化则会导致系统动力学特性转变。在自然界，灾变事件的扰动强度变化范围可能会达到几个数量级（如Ⅵ级地震到Ⅸ级地震能量相差达32 768倍），通过对SOC系统演化行为模式的深化认识，并与地质灾害实践建立联系，推动地质科学从唯象学向精确科学跨越，无疑是具有深远意义的工作。鉴此，本文研究期盼产生抛砖引玉之效。

[1]BAK P，CHEN K.Self-organized criticality[J].Scientific American，1991，264(1):26－33.

[2]BAK P，CHEN K，CREUTZ M.Self-organized criticality in the'Game of Life'[J].Nature，1989，342:780－782.

[3]BAK P，TANG C，WIESENFELD K.Self-organized criticality:an explanation of 1/f noise[J].Physical Review Letters，1987，59(4):381－384.

[4]HELD G A，SOLINA D H，KEANE D T，et al.Experimental study of critical-mass fluctuations in an evolving sandpile[J].Physical Review Letters，1990，65(9):1120－1123.

[5]FRETTEV，CHRISTENSENK，MALTHESRENSSEN A，et al.Avalanche dynamics in a pile of rice[J].Nature，1996，379(27):49－52.

[6]BRETZ M，CUNNINGHAM J B，KURCZYNSKI P L，et al.Imaging of avalanches in granular materials[J].Physical Review Letters，1992，69(16):2431－2434.

[7]OLAMI Z，FEDER H J S，CHRISTENSEN K.Self-organizedcriticalityinacontinuous，nonconservativecellularautomatonmodeling earthquakes[J].Physical Review Letters，1992，68(8):1244－1247.

[8]CHRISTENSEN K，OLAMI Z.Scaling，phase transitions，and nonuniversality in a self-organized critical cellularautomaton model[J].Physical Review A，1992，46(4):1829－1838.

[9]於崇文.固体地球系统的复杂性与自组织临界性[J].地学前缘，1998，5(3):159－182.YU Chong-wen.Complexity and self-organized criticality of solid earth system[J].Earth Science Frontiers，1998，5(3):159－182.

[10]姚令侃，黄渊，陆阳.自组织临界性及其在斜坡重力作用灾害研究中的应用[J].中国科学(E辑):2003，(33):17－27.YAO Ling-kan，HUANG Yuan，LU Yang.Self-organized criticality and its application in the slope disasters under gravity[J].Science in China (Series E)，2003，(33):17－27.

[11]SOMFAI E，CZIROK A，VICSEK T.Power-law distribution of landslides in an experiment on the erosion of a granular pile[J].Journal of Physics A:Mathematical and General，1994，27(20):757－763.

[12]KATZ O，AHARONOV E.Landslides in vibrating sand box:What controls types of slope failure and frequency magnitude relations?[J].Earth and Planetary Science Letters，2006，247(3):280－294.

[13]杨庆华，姚令侃，齐颖，等.散粒体离心模型自组织临界性及地震效应分析[J].岩土工程学报，2007，29(11):1630－1635.YANG Qing-hua，YAO Ling-kan，QI Ying，et al.Analysis of self-organized criticality of centrifugal model tests on granular mixtures and earthquake effect[J].Chinese Journal of Geotechnical Engineering，2007，29(11):1630－1635.

[14]CHOPARD Bastien，DROZ Michel.物理系统的元胞自动机模拟[M].祝玉学，赵学龙，译.北京:清华大学出版社，2003:10－13.

[15]黄润秋，李为乐.汶川大地震触发地质灾害的断层效应分析[J].工程地质学报，2009，17(1):19－28.HUANG Run-qiu，LI Wei-le.Fault effect analysis of geo-hazard triggered by Wenchuan earthquake[J].Journal of Engineering Geology，2009，17(11):19－28.

[16]刘汉香，许强，候红娟.岩性及岩体结构对斜坡地震加速度响应的影响[J].岩土力学，2013，34(9):2482－2488.LIU Han-xiang，XU Qiang，HOU Hong-juan.Influence of lithology and rock structure on slope seismic acceleration responses[J].Rock and Soil Mechanics，2013，34(9):2482－2488.

[17]姚令侃，方铎.非均匀砂自组织临界性及其应用研究[J].水利学报，1997，(3):23－32.YAO Ling-kan，FANG Duo.Study on the self-organized criticality of non-uniform sands and its application[J].Journal of Hydraulic Engineering，1997，(3):23－32.

[18]YAO L K，FANG D.On the self-organized criticality of non-uniform sands[J].International Journal of Sediment Research，1998，13(3):19－24.

[19]姚令侃，李仕雄，蒋良潍.自组织临界性及其在散粒体研究中的应用[J].四川大学学报(工程科学版)，2003，35(1):8－14.YAO Ling-kan，LI Shi-xiong，JIANG Liang-wei.Self-organized criticality and its application in granular mixtures[J].JournalofSichuanUniversity(Engineering Science Edition)，2003，35(1):8－14.