一种有限元转化为颗粒离散元的方法及其应用研究

冯 春，李世海，刘晓宇

（中国科学院力学研究所 流固耦合系统力学重点实验室，北京 100190）

1 引 言

地质灾害的形成过程是地质体从连续介质到非连续介质的渐进破坏过程。地质体内部裂纹的萌生、扩展、交汇、贯通，表征了地质灾害发展演化的不同阶段[1]。地质体中多裂纹扩展过程的数值模拟是当前国内外学术界的研究热点及难点。其中，有限元法及离散元法是两类主要的数值模拟方法。

有限元法以连续介质力学为基础，能够很好地描述地质体的弹塑性变形，适用于判断地质体从稳定到不稳定的临界点。为了分析地质体中裂缝的扩展演化过程，需在有限元方法中引入新的计算思路，如自适应网格及扩展有限元。自适应网格根据计算获得的裂纹起裂方向对初始网格进行局部细化及调整，使细化后的网格边界沿着裂纹扩展的方向，从而实现裂纹扩展过程的模拟[2－3]。此类方法在计算复杂工程问题时，涉及大量网格的重新划分及调整，算法稳定性差，计算效率低下，且新网格下各类场信息不能完全有效继承，往往会出现数值振荡现象。扩展有限元法通过引入跳跃函数实现有限元单元内部的非连续变形及隐式裂纹的扩展[4－6]，该方法具有严格的数学推导，但只能描述有限条裂纹的扩展过程，且在模拟裂纹交汇、分叉及三维裂缝扩展方面不尽如人意。

离散元法以非连续介质力学为基础，较为适合模拟地质体破坏后的运动解体过程，块体离散元及颗粒离散元是两类主要的离散元方法。块体离散元法用块体表征连续介质单元（刚体单元或可变形单元），用块体间的交界面表征非连续单元，通过块体边界的断裂实现裂纹扩展过程的模拟[7－10]。此类方法的裂缝仅能沿着块体边界扩展，因此，网格依赖性严重；且块体界面刚度的物理意义并不明确。当然，通过单元切割法可在一定程度上解决网格依赖性问题[11－12]，利用结构层也可部分解决界面刚度的选取问题[1]。颗粒离散元法通过细观颗粒簇的集合表述连续介质的宏观特性，通过细观颗粒的断裂、滑移反映宏观裂缝的萌生、扩展过程[13－15]。由于颗粒排布的随机性，颗粒离散元中的裂缝可向任意方向扩展。然而，此类方法无法准确描述宏观介质的力学特性，细观与宏观参数的对应关系往往需要通过大量的数值试验进行标定[16]。

为了充分发挥有限元与颗粒离散元各自的优势，将有限元与颗粒离散元进行耦合计算是一条有效途径。Oñate等[17]对有限元与颗粒离散元耦合的计算方法进行了详细论述，并将该方法成功应用于单轴压缩、巴西劈裂、桩体刺入等典型岩土工程问题中；Rojek等[18]基于文献[17]提出了一种有限元与颗粒离散元局部区域重叠耦合的方法，通过渐变函数实现有限元与颗粒离散元的自然过渡，并将该方法成功应用于隧道岩体的切割计算中。然而，上述方法中有限元与颗粒离散元的耦合属于分区耦合，变形破坏区用颗粒离散元进行描述，弱变形区用有限元进行描述。由于在强变形区采用了颗粒离散元，该区域初始状态下的宏观应力-应变依然无法准确描述。

因此，本文提出了一种有限元转化为颗粒离散元的方法，数值模型首先用较粗的有限元网格进行离散，当达到破坏条件，删除有限元单元，引入颗粒离散元，并利用颗粒离散元实现地质体渐进破坏过程的模拟。

2 有限元转化为颗粒离散元的方法

2.1 主要思路

首先将研究区域用较粗的有限元单元进行离散，每个单元按照虎克定律进行应力-应变的计算。当某个单元的应力状态满足Mohr-Coulomb准则或最大拉应力准则时，删除该单元，并在该单元所在位置创建具有一定数目、随机分布且微嵌入的颗粒系统。所创建颗粒的材料性质、速度、位移、接触力等信息根据插值函数从单元中继承。而后利用颗粒间接触力的演化自然实现宏观裂纹的萌生、扩展及贯通过程。具体的转化方法如图1所示。

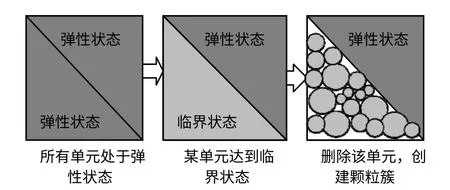
图1 有限元转化为颗粒离散元的基本思路Fig.1 Basic idea for transiting FEM into particle DEM

2.2 有限元的求解

本文在有限元计算时采用显式求解策略，主要包含节点合力计算及节点运动计算两个部分。节点合力计算为

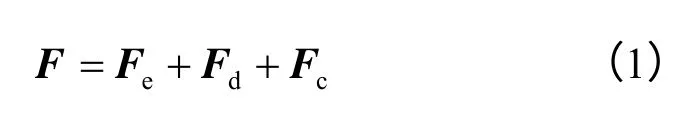
式中：F为节点合力；Fe为节点外力；Fd为节点变形力（由单元应力贡献）；Fc为阻尼力。

节点运动计算式为

式中：a为节点加速度；v为节点速度；Δu为节点位移增量；u为节点位移全量；m为节点质量；Δt为计算时步。基于式（1）、（2）的交替计算，即可实现有限元的显式求解过程。

本文采用增量法进行单元应力及节点变形力的计算：

式中：[ B ]i、{Δ ε }i、{Δ σ}i、 wi、 Ji分别为高斯点i 的应变矩阵、增量应变向量、增量应力向量、积分系数及雅克比行列式的值；{σn}i及{σo}i为高斯点i 当前时刻及上一时刻的应力全量；[ D ]、{Δ u }e、{ Fd}e分别为单元的弹性矩阵、节点增量位移向量及节点力向量；N为高斯点个数。

基于式（3），通过实时更新应变矩阵[ B]i及节点坐标[19]，可以实现有限元大位移（包含转动及平动）、大变形问题的计算。

2.3 临界条件

当某单元满足临界条件时，该单元即被删除，并创建颗粒簇。本文采用Mohr-Coulomb准则及最大拉应力准则作为临界条件，具体为

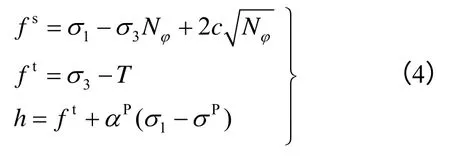
式中：σ1及σ3为最小及最大主应力；c、φ、T为黏聚力、内摩擦角及抗拉强度；Nφ、αp、σp为常数。

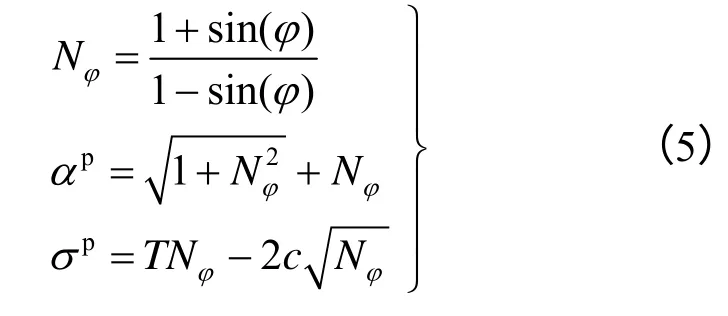
如果fs≤ 0且h≤ 0，则发生剪切破坏；如果ft≥ 0且h ＞ 0，则发生拉伸破坏。

2.4 颗粒生成

当有限元单元满足临界条件被删除后，需在有限元单元所在区域产生一定数量、随机分布且微嵌入的颗粒系统。首先对颗粒半径进行随机，随机模式为均匀分布模式，设平均半径为，则颗粒半径的分布范围为

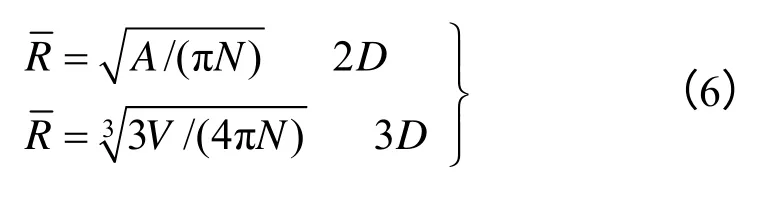
式中：A为二维颗粒的面积；V为三维颗粒的体积；N为产生的颗粒总数。

接着对颗粒体心的坐标进行随机，随机模式亦为均匀分布模式。当颗粒i 的体心坐标位于有限元单元内部，且颗粒i 到该单元所有面（棱）j 的距离及到所有已经创建的颗粒k 的距离均满足式（7）时，即创建颗粒i。

式中：Dij为颗粒i 到单元第j 个面（棱）的距离；dik为颗粒i 到第k 个颗粒的距离；Ri为颗粒i 的半径；Rk为颗粒k 的半径；tol为嵌入量（正值）。

颗粒i 创建后，其质量、材料参数、速度、位移、接触刚度、接触力等信息均需从有限元单元中继承。颗粒质量由有限元单元的密度乘以颗粒体积或面积获得；颗粒的黏聚力、内摩擦角及抗拉强度值从有限元单元中完全继承。

颗粒的速度、位移可通过单元节点插值获得：

式中：vP、uP为颗粒速度、位移；Wj为单元第j个点的插值系数；为单元第j 个点的速度、位移；Ne为有限元单元的节点数。

假设颗粒间的接触为有限面积的接触（见图2），则颗粒间的接触刚度可根据颗粒的接触面积及有限元单元的弹性模量、剪切模量获得：

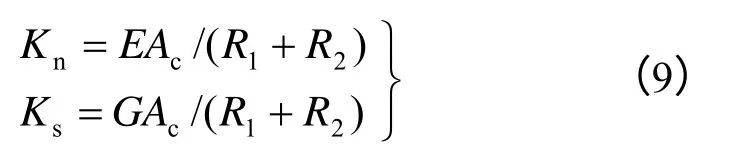
式中：Kn、Ks为颗粒间的法向及切向刚度；R1、R2为两个接触颗粒的半径；E、G为有限元单元的弹性模量及剪切模量；Ac为颗粒间的接触面积（可通过式（10）计算）。

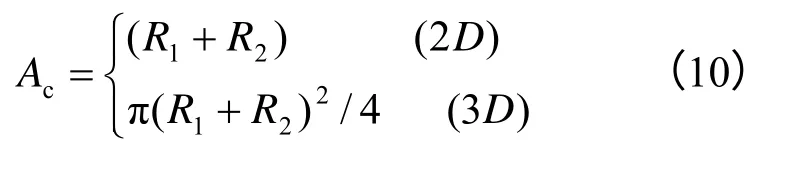
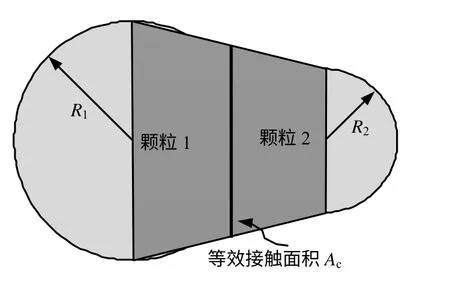
图2 颗粒间的有限接触模型Fig.2 Finite contact model between particles

颗粒间的初始接触力可通过插值获得的位移进行计算：

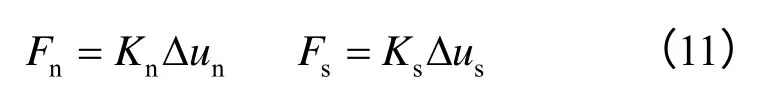
式中：Fn、Fs为颗粒间的法向及切向接触力；Δun、Δ us为两个接触颗粒间的法向及切向位移差。

2.5 颗粒离散元的计算

本文在颗粒离散元计算时同时考虑力与力矩的传递作用，两者的计算均基于增量法，且采用显式求解方式。颗粒离散元间接触力的计算式为

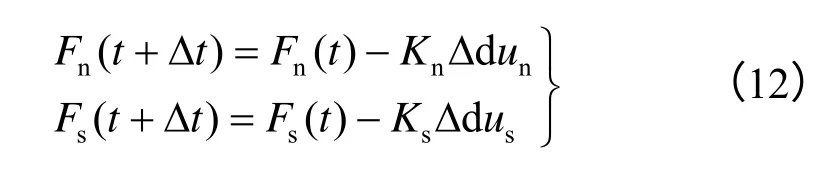
式中：Δdun、Δdus分别为两个接触颗粒间的法向及切向位移增量差。

接触力矩的计算式为

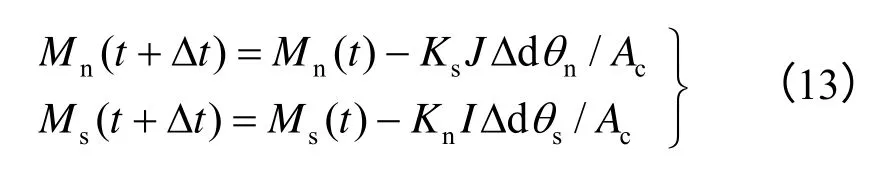
式中：Mn、Ms为扭矩及弯矩；I 和J为接触面的惯性矩及极惯性矩；Δdθn及Δdθs为颗粒间的扭转及弯曲转角增量差。

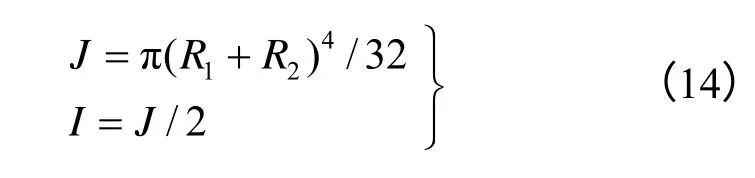
基于式（12）获得当前时步的试探接触力后，需根据Mohr-Coulomb准则及最大拉应力准则对接触力进行修正（法向力以压为正）：

当满足不等式（16）中的任何一个式子时，颗粒间的接触将不再传递力矩（即不进行式（13）的计算）。其中

为了更加真实地模拟细观颗粒的运动破坏过程，本文在计算时考虑了颗粒的转动效应（计算示意图如图3所示。

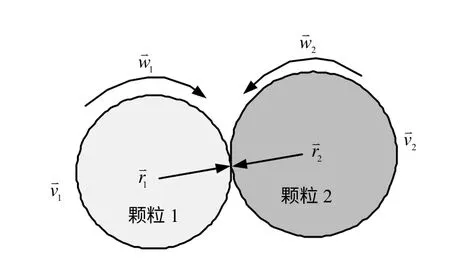
图3 颗粒的转动计算模型Fig.3 Particle-rolling computational model

计算时，首先利用式（17）获得全局增量位移向量Δd，接着将Δd 转换至接触局部坐标系，利用式（12）、（15）获得局部坐标系下的接触力，进而将接触力转化至整体坐标系，并利用式（18）计算施加至颗粒1、2上的转矩。

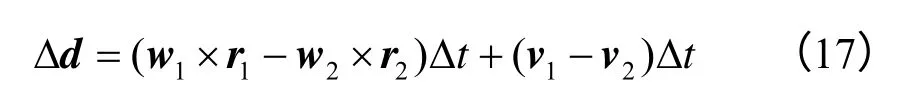
式中：w1及 w2为颗粒1、2的转动角速度向量；r1、r2为颗粒1、2到接触点的相对位置向量（由颗粒质心指向接触点）；v1、v2为颗粒1、2质心处的平动速度向量。

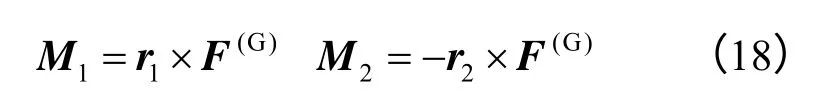
式中：M1、M2为施加至颗粒1、2上的转矩；F(G)为全局坐标下的接触力。

2.6 有限元与离散元的耦合

本文采用接触模型进行有限元与颗粒离散元的耦合。接触模型包含接触检测及接触力的计算两个部分，接触力的计算仍然采用增量法进行，与颗粒-颗粒间的接触力计算基本一致，在此处不再赘述。

接触检测包含初步及精确检测两个步骤。初步检测采用子空间法实现，通过颗粒、单元与格子的映射关系缩小搜索范围。精确检测根据数值模型的维度可分为两类：对于二维问题，实际上是颗粒与有限元边界棱之间的接触，采用点-棱接触模型进行描述；对于三维情况，实际上是有限元与边界面之间的接触，采用点-面接触模型进行描述。

点-棱接触（见图4）的创建需同时满足两个条件；一是颗粒质心到边界棱的距离（式（19））小于等于颗粒半径(d ≤ R)；二是颗粒质心在边界棱上的投影点位于棱的内部( dik≤ dij，djk≤ dij)。其中，Vpi为i 指向颗粒p 的相对位置向量，n为棱的单位外法向量。一旦颗粒与某边界棱建立了接触关系，法向弹簧及切向弹簧将自动创建，接触点k 的插值系数也将通过式（20）自动求解。

图4 点-棱接触模型Fig.4 Point-edge contact model

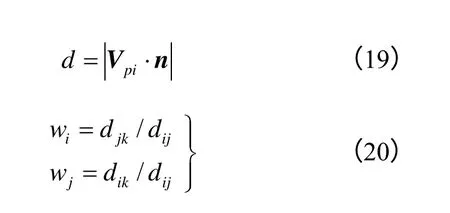
点-面接触（见图5）的创建与点-棱接触的创建过程基本一致。首先需判断颗粒到某边界面的距离是否小于颗粒半径；接着将颗粒质心点投影至边界面上，判断投影点是否位于某边界面的内部。如果上述两个条件均满足，则建立点-面接触，进而利用形函数计算接触点的插值系数。

图5 点-面接触模型Fig.5 Point-face contact model

考虑到三维有限元的边界面只有三角形及四边形两种形式，因此，可利用式（21）判断某投影点是否位于三角形内，利用式（22）判断某投影点是否位于四边形内。

式中：A为面积；ς为容差。

3 算 例

3.1 颗粒球与有限元厚板的碰撞分析

利用有限元转化为颗粒离散元进行岩体渐进破坏过程的分析，有限元与颗粒之间的接触计算不可避免。本算例通过颗粒球下落与有限元厚板的碰撞分析，验证颗粒与有限元接触模型的正确性。数值模型如图6所示。有限元厚板长为10 m，宽为10 m，厚为0.5 m，由2 968个四面体单元组成；颗粒球直径为6 m，球心位于厚板正上方5 m处，由1 277个颗粒组成，颗粒平均半径为0.15 m。颗粒在重力作用下向Y 轴负方向运动，有限元板不考虑重力，并对板X=0 m及X=10 m处的节点进行全约束。颗粒的弹性模量为0.1 GPa，泊松比为0.22，密度为2.5 g/cm3，内摩擦角为20°，黏聚力及抗拉强度为0 MPa；有限元板的弹性模量为3 MPa，泊松比为0.25，密度为2.5 g/cm3。颗粒下落及与有限元厚板的接触碰撞过程如图7所示。由图可得，随着颗粒球与有限元板的接触，颗粒球逐渐散开，有限元厚板出现较大变形；整个计算过程中颗粒与有限元之间未出现嵌入情况，且颗粒球与有限元厚板的运动与物理过程相符，证明了颗粒与有限元单元间接触模型的正确性。

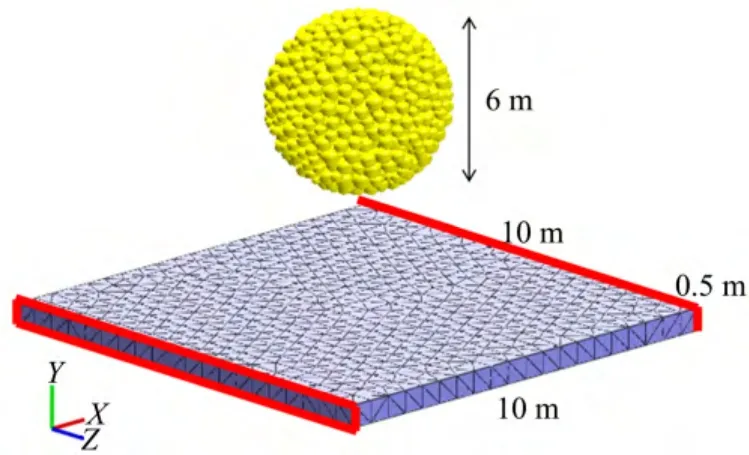
图6 颗粒球与厚板碰撞模型Fig.6 Impact model for a particle ball on a slab

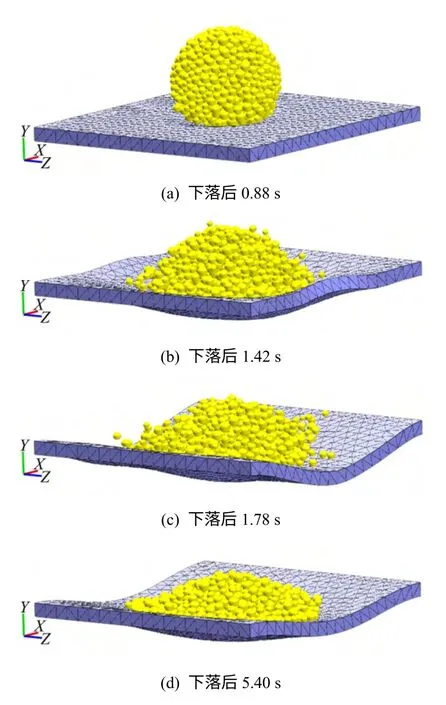
图7 碰撞过程描述Fig.7 Description of impacting process

3.2 岩石单轴压缩试验模拟

建立10 cm×20 cm的岩石试样，用468个三角形单元进行剖分。模型底部全约束，模型顶部施加准静态竖直向下的速度载荷。采用传统有限元及有限元转化为颗粒离散元等两种思路进行岩石渐进破坏过程的模拟。岩石弹性模量为30 GPa，泊松比为0.25，密度为2.5 g/cm3，抗拉强度及黏聚力均为3 MPa，内摩擦角为30°。利用传统有限元进行模拟时，采用Mohr-Coulomb理想弹塑性模型及关联流动法则。

单轴压缩过程中，上述两种方法给出的岩石应力-应变的关系如图8所示。由图可得，在初期阶段，两种方法获得的应力-应变曲线基本一致，轴向应力均随着轴向应变的增加而线性增加。到达临界状态后，随着轴向应变的增加，传统有限元方法给出的轴向应力将保持不变，岩石出现理想弹塑性压剪变形；而本文所述方法获得的轴向应力将迅速减小为0，岩石发生脆性压剪破坏。由此，与传统的有限元方法相比，本文所述方法可以更为真实地反映岩石单轴压缩过程中的脆性破坏过程。

此外，本文所述方法获得的峰值应力约为10.15 MPa，与式（23）估算的临界值（10.39 MPa）基本一致，表明了本文所述算法的准确性。

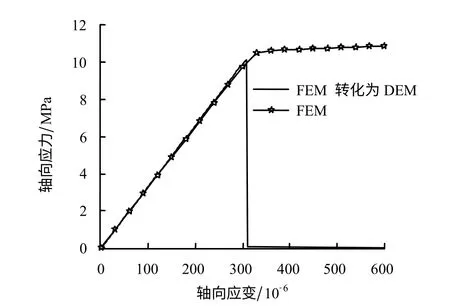
图8 岩石的应力-应变曲线Fig.8 Strain-stress curves of rock

利用有限元转化为离散元方法计算获得的岩石失稳后的破裂形态如图9所示。由图可知，岩石在准静态竖向载荷作用下，发生了明显的X型剪切破坏，破坏单元被一系列颗粒所填充，并由这些填充的颗粒完成了后续的破裂演化过程。

利用传统有限元方法获得的岩石失稳后的水平方向位移及塑性剪应变云图如图10所示。由图可得，水平位移及塑性剪应变均呈现出明显的X型破坏特征，但材料并没有发生断裂，仍然处于连续变形状态。

图9 岩石的破裂形态Fig.9 Rock failure pattern

图10 有限元计算获得的水平位移及塑性剪应变云图Fig.10 Contours of X-displacement and shear plastic strain based on the FEM method

3.3 岩石切割过程模拟

岩石尺寸为0.2 m×0.4 m，由112个有限元单元进行离散；刀头为三角形，三边的长度分别为6.8、10.8、11.1 cm。岩石底部全约束，刀头以10 m/s的切割速度向岩石推进。岩石的弹性模量为30 GPa，泊松比为0.25，密度为2.5 g/cm3，黏聚力为5 MPa，内摩擦角为40°，抗拉强度为2 MPa。切割过程中岩石的渐进破坏过程如图11所示。岩石顶部左右两侧节点P1及P2（具体位置见图11）的水平位移随时间的变化曲线如图12所示。

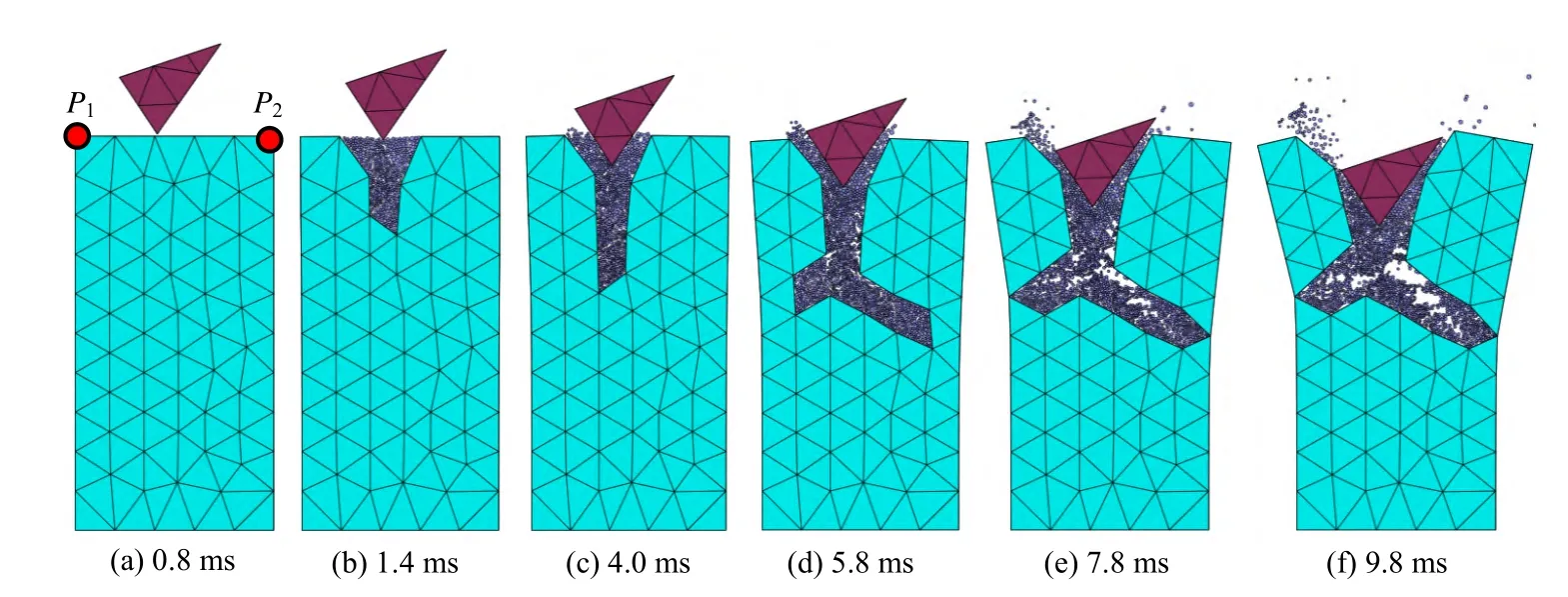
图11 岩石切割破裂过程Fig.11 Rock failing process during cutting

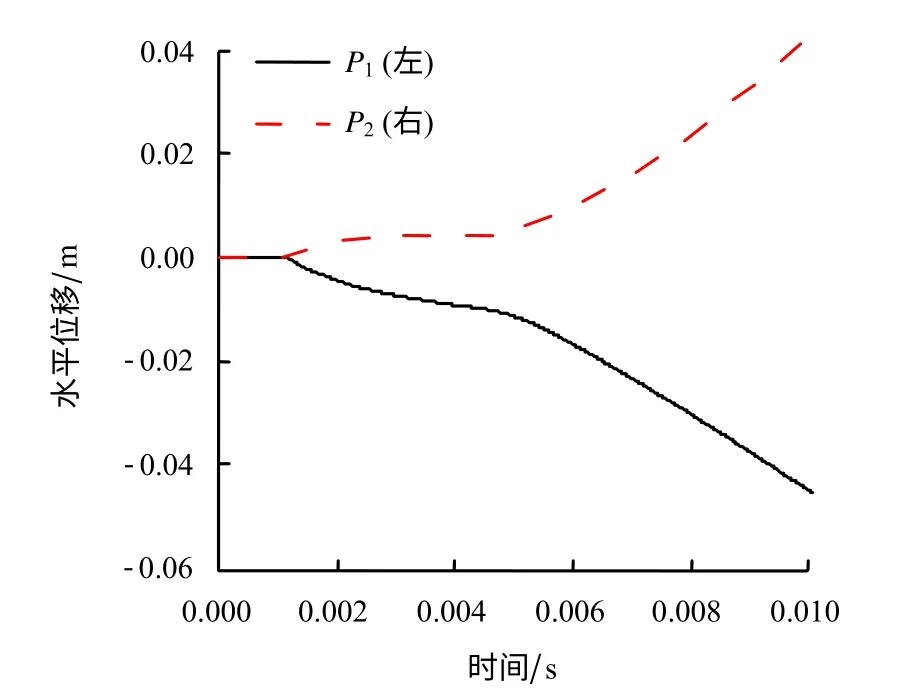
图12 节点P1及P2的水平位移时程曲线Fig.12 X-displacement vs.time at points P1and P2

由图11可知，随着刀片的推进，刀片附近的岩石逐渐破碎，转化为颗粒流；岩石中宏观裂缝的扩展过程通过颗粒之间的细观接触力演化自然获得。由图12可知，随着时间的推移，岩石顶部左、右两侧节点P1、P2的水平位移逐渐增大；当4.8 ms以后，位移的增加速率明显增大，表明此时岩石已经出现了失稳破坏。图11、12展示的岩石破裂过程及位移时程曲线与实际较为相符，证明了本文所述方法的合理性。

4 结 论

（1）本文所述有限元与颗粒离散元的耦合转化模型，结合了有限元与颗粒离散元各自的优势，较为适合模拟地质体在各类静、动载荷作用下的渐进破坏过程。

（2）在有限元与颗粒离散元的耦合转化模型中，地质体初期的宏观应力-应变由有限元计算，地质体后期的渐进破坏过程由颗粒离散元模拟；并利用Mohr-Coulomb准则及最大拉应力准则进行转换点的判断。

（3）颗粒球与有限元板的碰撞分析、岩石单轴压缩过程模拟、岩石切割过程模拟等案例，证明了有限元与颗粒离散元接触模型、转化模型的合理性及正确性。

（4）有限元与颗粒离散元耦合转化模型的后续研究重点将包括如下几个方面：转化点所用宏观准则的优选、随机颗粒系统生成方案的优选、颗粒不同信息继承方式的对比、本文所述方法的进一步校核（与试验及其他数值模拟方法的对比），利用本文方法进行三维岩体渐进破坏过程的模拟等。

[1]李世海，刘天苹，刘晓宇.论滑坡稳定性分析方法[J].岩石力学与工程学报，2009，28(增刊2):3309－3324.LI Shi-hai，LIU Tian-ping，LIU Xiao-yu.Analysis method for landslide stability[J].Chinese Journal of Rock Mechanics and Engineering，2009，28(Supp.2):3309－3324.

[2]MIEHE C，GÜRSES E.A robust algorithm for configurational-force-driven brittle crack propagation with R-adaptive mesh alignment[J].International Journal for Numerical Methods in Engineering，2007，72(2):127－155.

[3]KHOEI A R，AZADI H，MOSLEMI H.Modeling of crack propagation via an automatic adaptive mesh refinement based on modified superconvergent patch recovery technique[J].Engineering Fracture Mechanics，2008，75(10):2921－2945.

[4]DOLBOW J，BELYTSCHKO T.A finite element method for crack growth without remeshing[J].International Journal for Numerical Methods in Engineering，1999，46:131－150.

[5]ASADPOURE A，MOHAMMADI S.Developing new enrichment functions for crack simulation in orthotropic media by the extended finite element method[J].International Journal for Numerical Methods in Engineering，2007，69(10):2150－2172.

[6]GORDELIY E，PEIRCE A.Implicit level set schemes for modeling hydraulic fractures using the XFEM[J].Computer Methods in Applied Mechanics and Engineering，2013，266:125－143.

[7]JIANG Y，LI B，YAMASHITA Y.Simulation of cracking near a large underground cavern in a discontinuous rock mass using the expanded distinct element method[J].International Journal of Rock Mechanics and Mining Sciences，2009，46(1):97－106.

[8]AMARASIRI A L，KODIKARA J K.Numerical modelling of desiccation cracking using the cohesive crack method[J].International Journal of Geomechanics，2011，13(3):213－221.

[9]BARLA M，PIOVANO G，GRASSELLI G.Rock slide simulation with the combined finite-discrete element method[J].International Journal of Geomechanics，2011，12(6):711－721.

[10]LI SH，ZHAO MH，WANG YN，et al.A new numerical method for DEM-block and particle model[J].International Journal of Rock Mechanics and Mining Sciences，2004，41(3):436－436.

[11]COTTRELL M G，YU J，WEI Z J，et al.The numerical modelling of ceramics subject to impact using adaptive discrete element techniques[J].Engineering Computations，2003，20(1):82－106.

[12]王杰，李世海，周东，等.模拟岩石破裂过程的块体单元离散弹簧模型[J].岩土力学，2013，34(8):2355－2362.WANG Jie，LI Shi-hai，ZHOU Dong，et al.A blockdiscrete-spring model to simulate failure process of rock[J].Rock and Soil Mechanics，2013，34(8):2355－2362.

[13]VESGA L F，VALLEJO L E，LOBO GUERRERO S.DEM analysis of the crack propagation in brittle clays under uniaxial compression tests[J].International Journal for Numerical and Analytical Methods in Geomechanics，2008，32(11):1405－1415.

[14]YANG D，SHENG Y，YE J，et al.Dynamic simulation of crack initiation and propagation in cross-ply laminates by DEM[J].Composites Science and Technology，2011，71(11):1410－1418.

[15]UTILI S，NOVA R.DEM analysis of bonded granular geomaterials[J].International Journal for Numerical and Analytical Methods in Geomechanics，2008，32(17):1997－2031.

[16]YANG B，JIAO Y，LEI S.A study on the effects of microparameters on macroproperties for specimens created by bonded particles[J].Engineering Computations，2006，23(6):607－631.

[17]OÑATE E，ROJEK J.Combination of discrete element and finite element methods for dynamic analysis of geomechanics problems[J].Computer Methods in Applied Mechanics and Engineering，2004，193(27):3087－3128.

[18]ROJEK J，OÑATE E.Multiscale analysis using a coupled discrete/finite element model[J].Interaction and Multiscale Mechanics，2007，1(1):1－31.

[19]FENG C，LI SH，LIU XY，et al.A semi-spring and semi-edge combined contact model in CDEM and its application to analysis of Jiweishan landslide[J].Journal of Rock Mechanics and Geotechnical Engineering，2014，6(1):26－35.