稀疏条件下的两层分类算法
仝伯兵,王士同,梅向东
(1. 江南大学 数字媒体学院,江苏 无锡 214122; 2. 赞奇科技发展有限公司,江苏 常州 213000)
稀疏条件下的两层分类算法
仝伯兵1,王士同1,梅向东2
(1. 江南大学 数字媒体学院,江苏 无锡 214122; 2. 赞奇科技发展有限公司,江苏 常州 213000)
在有限样本下距离量的选择对最近邻算法(K-nearest neighbor,KNN)算法有重要影响。针对以前距离量学习泛化性不强以及时间效率不高的问题,提出了一种稀疏条件下的两层分类算法(sparsity-inspired two-level classification algorithm,STLCA)。该算法分为高低2层,在低层使用欧氏距离确定一个未标记的样本局部子空间;在高层,用稀疏贝叶斯在子空间进行信息提取。由于其稀疏性,在噪声情况下有很好的稳定性,可泛化性强,且时间效率高。通过在噪声数据以及在视频烟雾检测中的应用表明,STLCA算法能取得更好的效果。
稀疏贝叶斯;两层分类;距离学习;视频烟雾检测;最近邻算法;有限样本;泛化性;时间效率
在分类问题中,最近邻算法(K-nearest neighbor, KNN)是一种古老而又精确的确定决策边界的非线性分类算法。给定一组训练数据,KNN通过k个临近的样本中大多数标签集对未知样本进行预测。研究表明[1],最近邻规则的渐近错误率最多是贝叶斯分类错误率的2倍,而且跟所使用的距离量无关。
当训练集有无限数量的样本时,类条件概率在无穷小的未标记测试样本域中是常量而与所采用距离量的形式无关。由于欧氏距离在输入空间中具有均匀的各向同性的性质,因此,欧氏距离作为距离度量来确定最近邻样本是自然的选择。在缺乏先验知识的情况下,大多数基于KNN的方法使用简单的欧氏距离衡量样本间的相似性。然而,在现实情况下,无限数量的训练样本是不存在的。因此,在有限样本下,假设局部的类条件概率为常量是不成立的,这样欧氏距离在训练数据中不能充分利用统计规律。因而,选择一个合适的距离量来提高最近邻分类的性能变得至关重要。
在统计分类和信息检索中,距离度量的学习起到了很大的作用。例如,先前研究表明[2],适当的距离度量可以明显提升KNN算法的分类精度。大多数的距离度量学习可以分为以下两大类:1)基于判别分析的度量学习如Domeniconi 和 Gunopulos[3]提出一种利用支持向量机作为指导来定义一个局部灵活度量(local flexible metric classification based on SVMs , LFM-SVM)的方法。然而,利用核函数方式使转换数据从输入空间转换到高维特征空间时,数据不变性难以维持;2)基于统计分析的度量学习如Zhang 等[4]提出了一种通过知识嵌入从训练数据集中学习距离度量的算法。由于它们位置接近而且局部特征具有相似性,使用新的距离度量可以确定输入空间中的未标记的测试样本近邻。Gao等[5]提出了一种基于自适应距离度量的两层最近邻分类算法(two-level nearest neighbor , TLNN),该算法在低层以欧氏距离定义一个局部子空间,然后在高层用AdaBoost算法进行信息提取,算法框架如图1所示。AdaBoost算法是由Freund和Schipare[6-8]提出的一种高效的分类方法,然而AdaBoost在有噪声的情况下容易产生过度拟合导致泛化性差,而且由于AdaBoost进行弱分类器训练时需要对训练数据进行多次遍历,进而导致时间效率较低。
文中提出了一种在稀疏条件下的两层分类算法(sparsity-inspired two-level classification algorithm, STLCA)。在STLCA算法低层,先用欧氏距离定义一个未标记的样本局部子空间限制高层分类器过度延伸,然后在分类器的高层,用稀疏贝叶斯方法在未标记样本局部子空间进行信息提取,算法模型框架如图2所示。

图1 TLNN算法模型
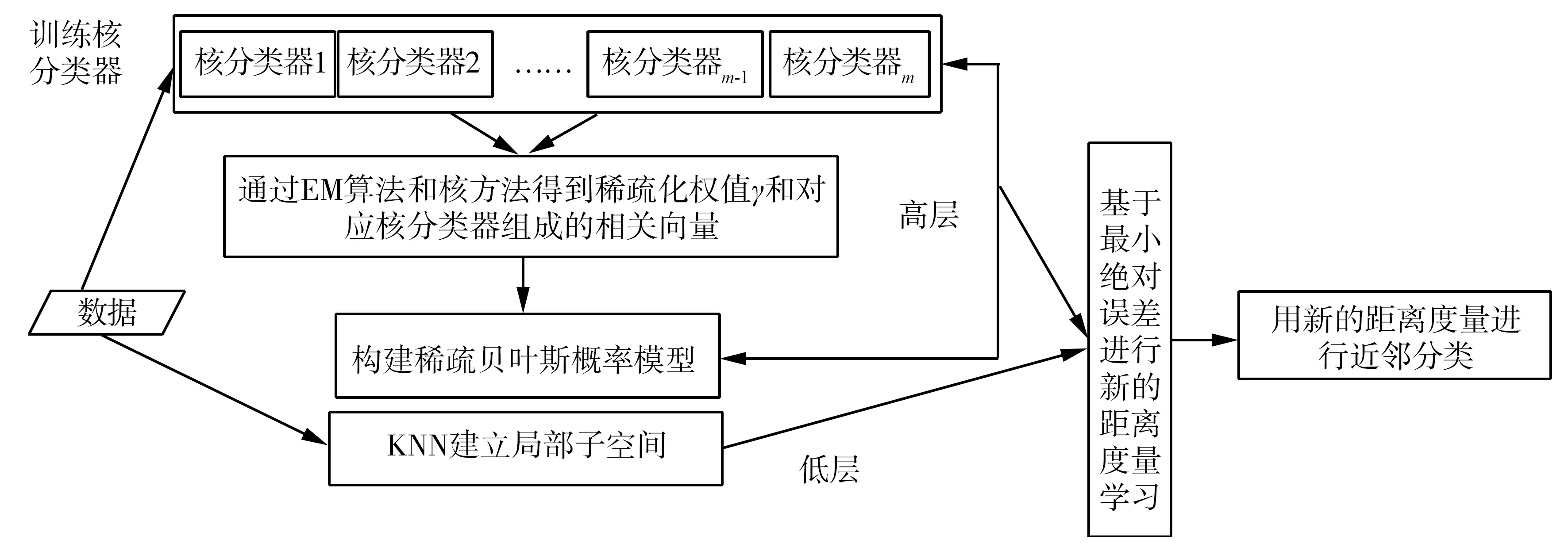
图2 STLCA算法模型
先构建核函数分类器,在求解权值过程中引入EM方法,根据稀疏贝叶斯理论使大部分权值趋于零,其对应的核函数样本组成相关向量,保证分类器稀疏性。由于其稀疏性,在噪声影响下也有很好的稳定性,且由于分类器不必多次遍历训练样本使得时间效率较高。将得到的权值与核分类器组建概率模型,利用最小绝对误差原则进行距离度量学习,将新距离量应用到最近邻算法中,构成一种新的强分类器STLCA算法。通过对比实验可知,STLCA算法在噪声数据和视频烟雾检测应用中有很好的效果。
1 方法模型
1.1 用最小绝对误差进行距离度量学习
设x是要预测的类标签未知的样本点,x′是x的最邻近点。对于一般的最近邻算法,未知样本x被错分的概率如式(1)[9]:
PN(e|x)=P(w1|x)P(w2|x′)+P(w2|x)P(w1|x′)=P(w1|x)[1-P(w1|x′)]+P(w2|x)P(w1|x′)=2P(w1|x)P(w2|x)+[P(w1|x)-P(w2|x)]·
式中:N表示训练样本的数量,w1,w2表示类标签,为了简便起见此处只考虑二分类,对于多分类问题通常转换成多级二分类问题来处理。当训练样本的数量N→时,渐近条件错误率为
这样,式(1)和式(2)都表示最近邻法的条件错误率,只不过式(1)针对有限样本,而式(2)是对无限样本而言,如果考虑两者之间的误差,式(3):
PN(e|x)-P(e|x)=[P(w1|x)-P(w2|x)]·
在有限样本或无限样本训练样本下的平均绝对误差的误差率为式(4):
定义式(5)为
那么式(5)中σ(x,x′)和P(w1|x)-P(w1|x′)之间的对应关系如图3所示。

图 3 σ(x,x′)线性关系图
由于[P(w1|x)-P(w2|x)]在式(3)中是一个常数项,那么最小化|PN(e|x)-P(e|x)|相当于最小化σ(x,x′)。通常可以通过增加训练样本的数量最小化σ(x,x′),或者定义一个等价距离量如文献[5]中所采用的方法。然而在这里所论述的,是想通过另外的方式求解。
在2类问题y∈{1,-1}中(此时规定标签w1=1,w2=-1),对于给定的x可以通过广义线性模型[10]确定属于某一类的概率:
式中:h(x)为分类器,γ为分类器权重向量。而此处Φ(z)为高斯累计分布函数(也被称为链接函数),其形式为式(7):
将概率模型的输入特征进行非线性转换可以应用到非线性函数中,对于权值向量γ其基本形式包括以下3种形式[10-11]:
1)线性分类器:h(x)=[1 x1… xd],此时γ是一个d+1维的向量;
2)非线性分类器:h(x)=[1 φ1(x) ... φk(x)]T,此处φ(·)是非线性函数,γ为k+1维向量;
3)核函数分类器:h(x)=[1 K(x,x(1)) … K(x,x(n))]T,此处K(·,·)为核函数,γ为n+1维向量。
如果能够得到γ值,那么就可以对变量x的标签做出预测。对于普遍使用的参数估计方法如最大似然函数法有式(8)的表现形式:
或拉普拉斯条件概率分布,如式(10):
式中:α是假设参数向量。由于不能从公式中直接获得参数γ,本文采用EM迭代方法获取参数γ。对于参数γ按式(10)的拉普拉斯条件概率分布,可采用下面EM迭代步骤进行求解(算法1):
1)对于给定的训练数据集计算矩阵H;此处采用核函数对矩阵进行运算,其中h(x)=[1 K(x,x(1)) … K(x,x(n))]T,
H=[hT(x1) hT(x2) … hT(xn)]T
2)计算γ的初始值,可以通过如下公式对γ 进行初始化:
式中:ε为初始参数,I为单位矩阵。
稀疏贝叶斯方法与给似然函数加上惩罚函数等方法的不同之处在于:稀疏贝叶斯方法在迭代优化的过程中能使大部分权值γi趋于零,其相应的核函数和训练样本被剔除,只保留少数的权值γi不为零,这样可以保证分类器的稀疏性,其对应的保留下来的训练样本称为相关向量(relevance vector, RV)。在概率模型中,一个重要的特性是该模型包含一个隐含变量即式(15)所示:
式中:η为均值为零单位方差的高斯变量。对于二分类问题,假设分类器定义为y=1如果z(x,γ)≥0,且y=-1当z(x,γ)<0。那么概率模型可以表示为式(16):
h(x)|0,1)=
P(γTh(x)+η≥0)
(16)
则式(5)可以表示为式(17):
σ(x,x′)=|P(1|x)-P(1|x′)|=
|Φ(γTh(x)|0,1)-Φ(γTh(x′)|0,1)|=
|P(γTh(x)+η≥0)-P(γTh(x′)+η≥0)|
(7)
则新的距离量可以改写为式(18):
D′(x,x′)=|P(γTh(x)+η≥0)-P(γTh(x′)+η≥0)|∝|sign(γTh(x)+η≥0)-sign(γTh(x′)+η≥0)|=
此时已经定义了一个新的距离量,下面将给出算法步骤。
1.2 稀疏条件下的两层分类算法
文中提出的稀疏条件下的两层分类算法。先用最近邻算法建立一个局部子空间,即在低层使用欧氏距离为每个测试数据选定k个近邻样本组成子空间,这样可以限制稀疏贝叶斯信息提取时过度延伸;然后在STLCA分类器的高层,用上文中的新距离量从子空间选定近邻来确定测试数据标签。稀疏贝叶斯算法通过EM迭代优化的方法对权值γ进行求解,使大部分权值趋于零,保证了分类器的稀疏性,在噪声情况下也有很好的稳定性。由于在求解过程中直接进行矩阵运算而不同于AdaBoost对训练集多次遍历评估弱分类器性能,因此时间效率较好。
综上所述,STLCA算法描述如下(算法2):
1)利用上文中的算法一对权值向量γ值进行参数估计;
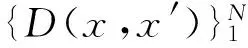

4)对于给定的观测值x判定其标签y:y=sign(avex′∈R′(x)y′)。
2 实验与分析
本次试验均在MATLAB7.10.0平台下完成,实验环境为CPU Intel Core(TM) i3-3240 3.40 GHz,内存4 GB。通过UCI数据集和视频烟雾2种数据对算法有效性进行对比验证。
2.1 UCI标准数据集
在本节中,使用真实数据集对几种算法进行比较以验证文中提出的算法和其他算法的分类效果及抗噪能力。从UCI数据库中挑选二分类数据集进行测试,数据类别标记为+1和-1,删除属性值缺失的实例,数据的基本信息如表1所示。

表1 UCI数据集的基本信息Table 1 Description of UCI dada sets
实验中所有训练数据特征先进行归一化到零均值和单位方差,测试数据使用相应的均值和方差进行归一化。将每个数据集随机分成2个大小相等的子集,使用其中一个子集作为训练集,另一个作为测试集,然后再将2个子集交换。将过程重复10次(10×2交叉验证),取平均值作为结果。在TLNN和STLCA算法中,近邻数量关系设置为k1=2·k2+1,此处设置k2=3。在AdaBoost与TLNN算法中,以单特征值训练泛化型AdaBoost的弱分类器,最大训练迭代次数T=30。在稀疏贝叶斯和STLCA算法求解向量γ值时,设置ε=10-6和δ=10-3,在计算矩阵H时,核宽值如表2所示。
2.2 STLCA算法比较与分析
将STLCA与AdaBoost、TLNN、KNN和稀疏贝叶斯进行对比,各算法分类错误率如表3所示。

表2 UCI数据集核宽值Table 2 Kernel width of UCI data sets
表3 UCI数据集分类错误率
Table 3 Classification error rate of UCI data sets%
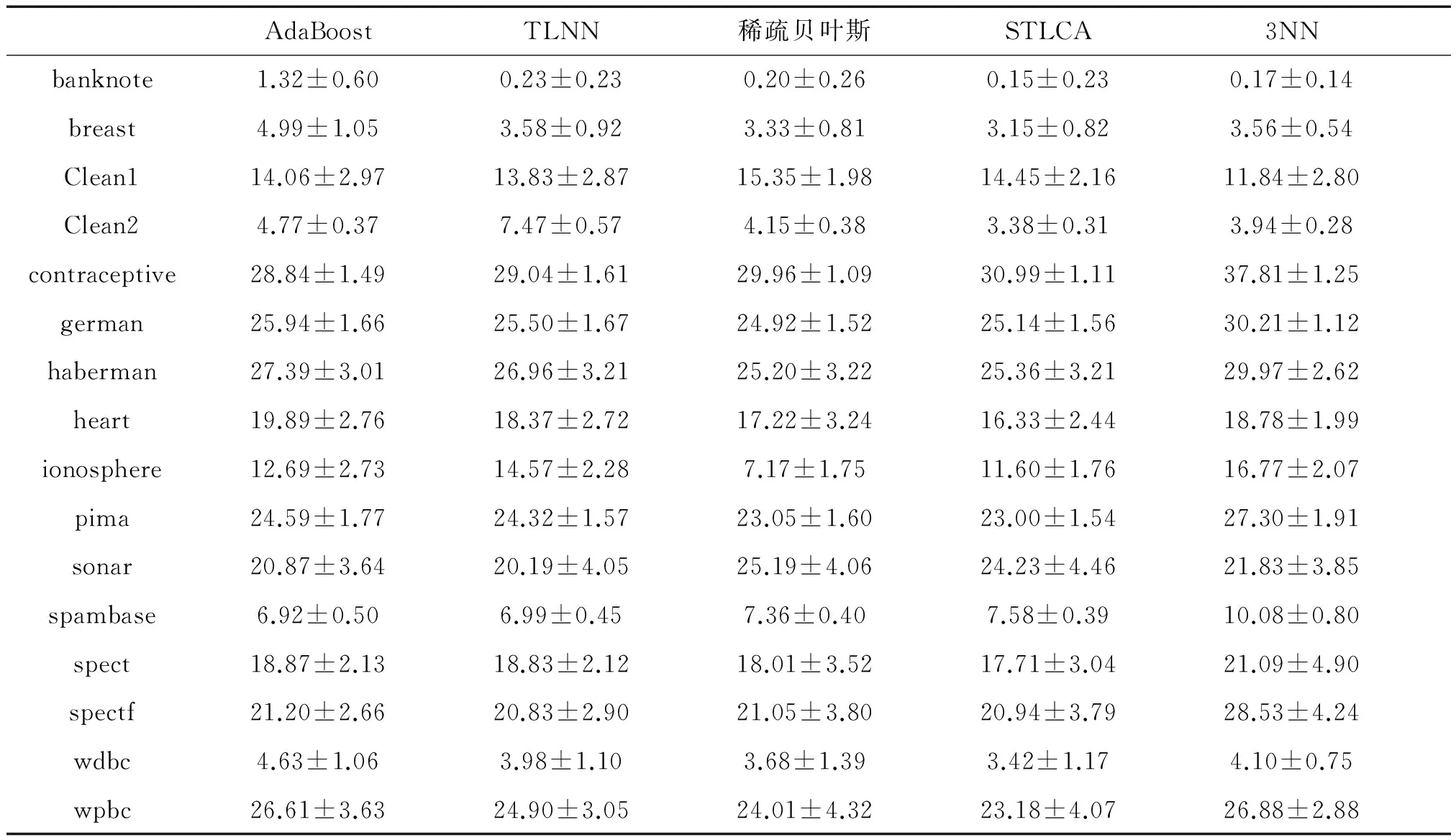
注:表中数值为错误率+标准差形式。
表3中显示了不同算法数据分类的错误率,文中将错误率最低的数据加黑。从实验结果看,在16组数据中,AdaBoost和TLNN算法各有2组数据取得最低错误率,KNN算法和稀疏贝叶斯算法分别有1组和3组数据取得最低错误率,而STLCA算法在8组数据中取得最优结果。在STLCA算法未取得最优结果的8组数据中仍有3组数据的实验结果优于稀疏贝叶斯方法,可见STLCA算法在分类精度上整体要优于TLNN和稀疏贝叶斯等方法。
任何现实的算法模型在样本学习中必须处理噪声问题,因此,有必要测试在噪声数据的影响下STLCA算法的性能。本文通过对表1中16组数据引入标签噪声来比较5种算法的抗噪性能。在训练集中随机挑选部分数据,然后调换它们的标签,而其他样本保持不变。这样构造5%、10%、15%、20%的随机噪声数据集。表4~7给出了4种不同噪声下5种算法分类错误率结果。
表4 5%噪声数据分类错误率
Table 4 Classification error rate with 5% noise%
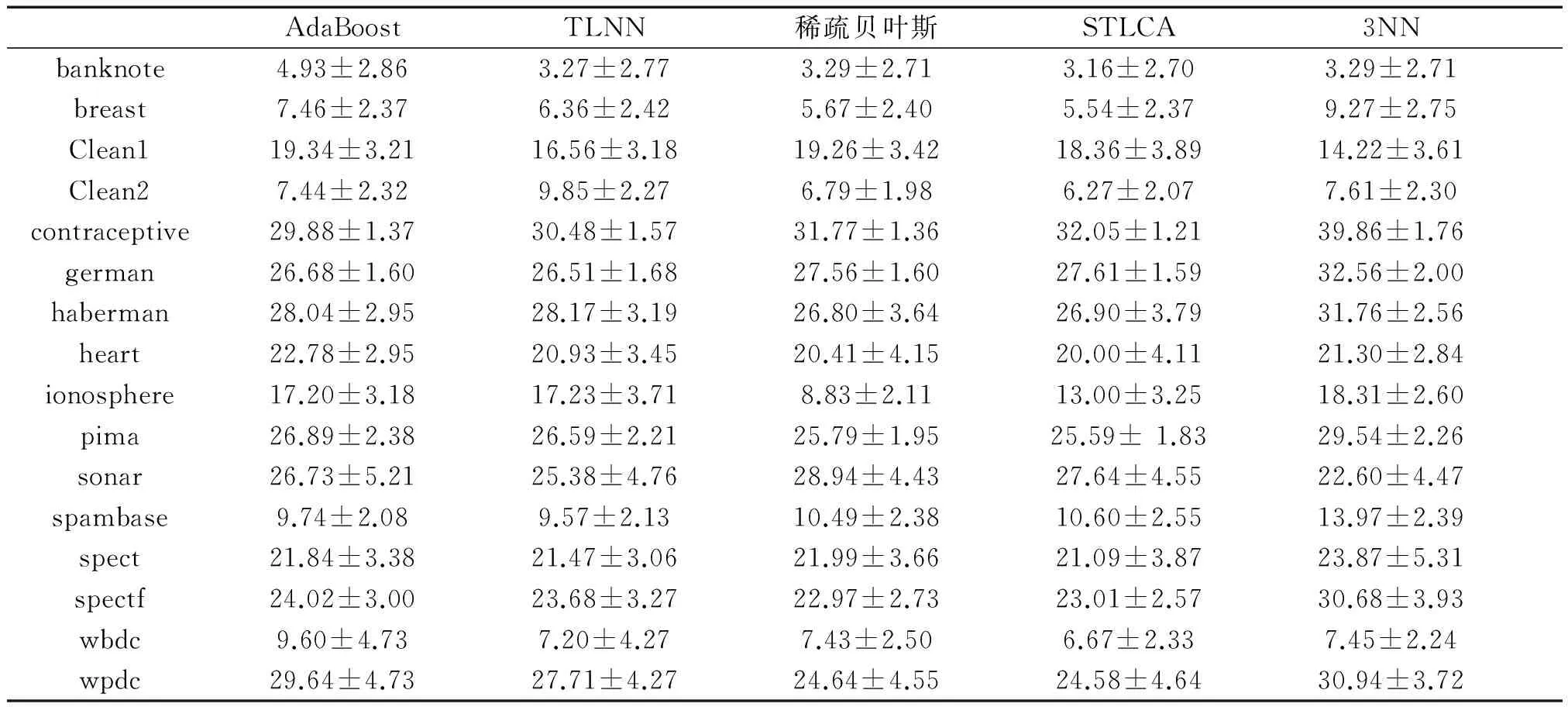
注:表中数值为错误率+标准差形式。

表5 10%噪声数据分类错误率Table 5 Classification error rate with 10% noise%
表6 15%噪声数据分类错误率
Table 6 Classification error rate with 15% noise%
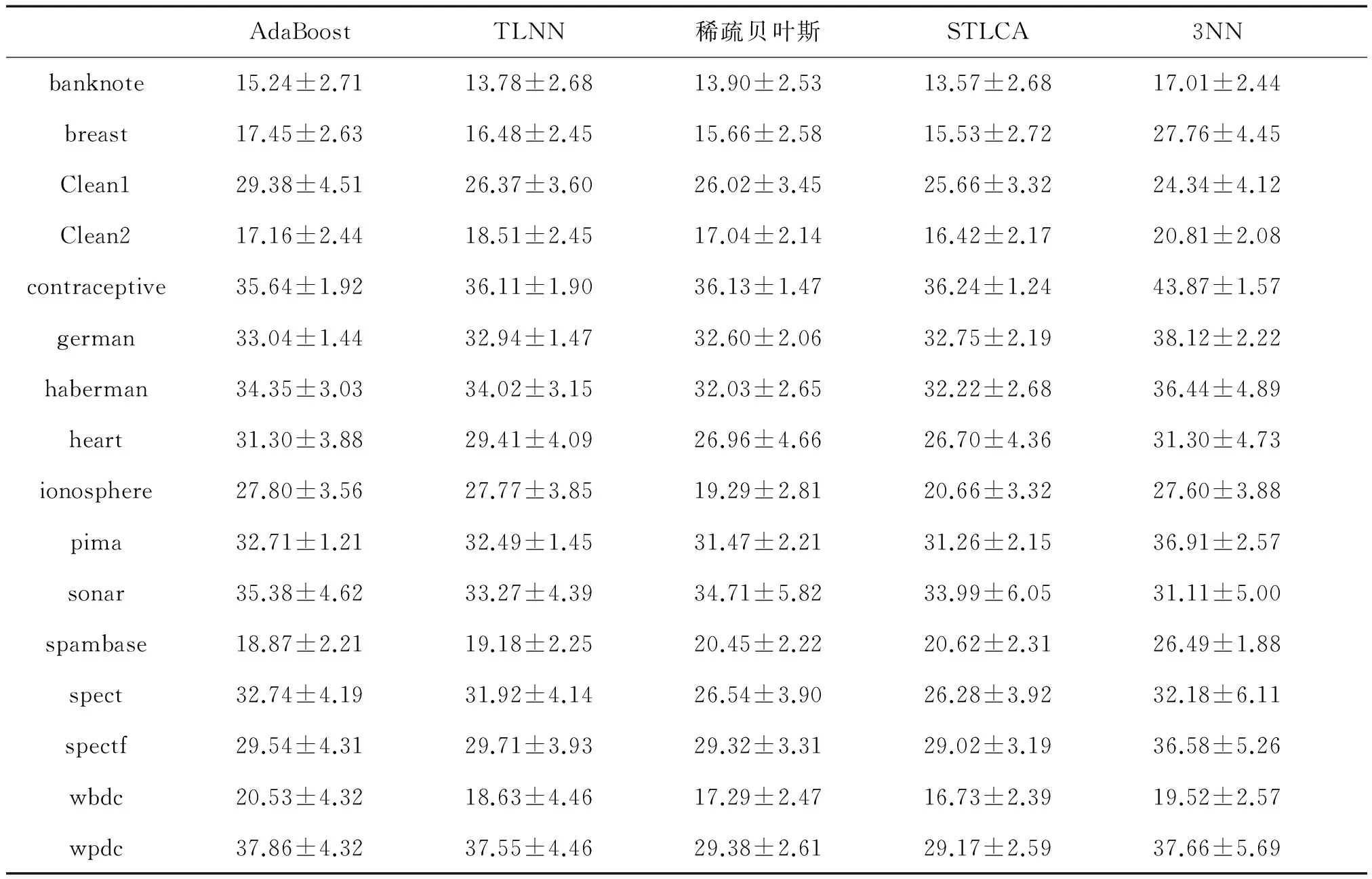
注:表中数值为错误率+标准差形式。
表7 20%噪声数据分类错误率
Table 7 Classification error rate with 20% noise%
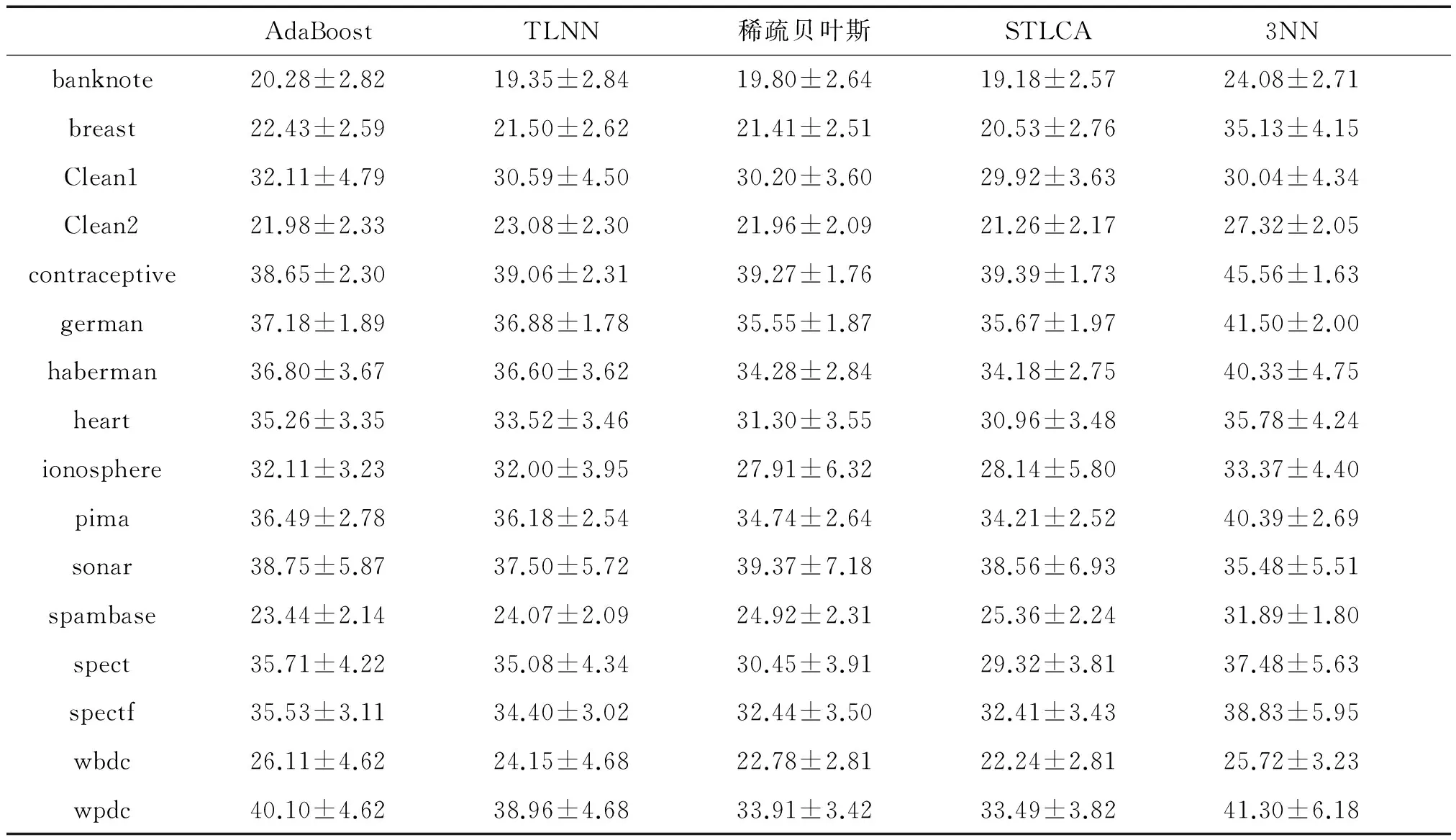
注:表中数值为错误率+标准差形式。
将表4~7给出的 5种算法在标签噪声分布数据错误率最低的数据加黑。从实验结果可以看出,AdaBoost算法在5%、10%、15%、20%的随机噪声数据集中分别有2组、1组、2组、2组数据中取得最优,然而除contraceptive数据集外,其他最优结果数据集并不一致,可见AdaBoost算法有一定波动性,容易受噪声影响。TLNN算法分别在1组、1组、0组、0组数据集中取得最优,表明TLNN算法在噪声条件下性能出现一定退化。稀疏贝叶斯和KNN算法未出现明显波动,性能较为稳定。而STLCA在标签噪声为5%、10%、15%和20%的结果中分别有8组、9组、9组和11组数据取得最优,随着噪声数据增加分类结果变优,表明STLCA算法在噪声情况下有很好的稳定性,泛化能力强。
2.3 视频烟雾检测
火灾严重威胁人类的生命和财产安全,因此及时检测和预防火灾具有重要意义, 在火灾监控中,烟雾检测对于实现早期火灾预警[15-17]具有重要作用。
文中将STLCA算法应用到视频烟雾检测中,以验证算法的检测效果。实验中的烟雾视频来源于土耳其Bilkent大学机器视觉研究室(http://signal.ee.bilkent.edu.tr/VisiFire/)视频资源库(http://imagelab.ing.unimore.it/visor/video_categories.asp)。图4所示为4组实验视频截取第60帧图像的场景,从左至右、从上至下依次为Video1~Video4。

图4 实验视频场景
视频分辨率为240×320,实验中将每一帧图像分为60像素×60像素的小块,因此图像被分为3×4块。实验中每组图像数据为从相应视频中每6帧取一帧图像组成数据集,然后将每个数据集随机分成2个大小相等的子集,其中一个为训练集,另一个为测试集,数据集详细信息如表8所示。
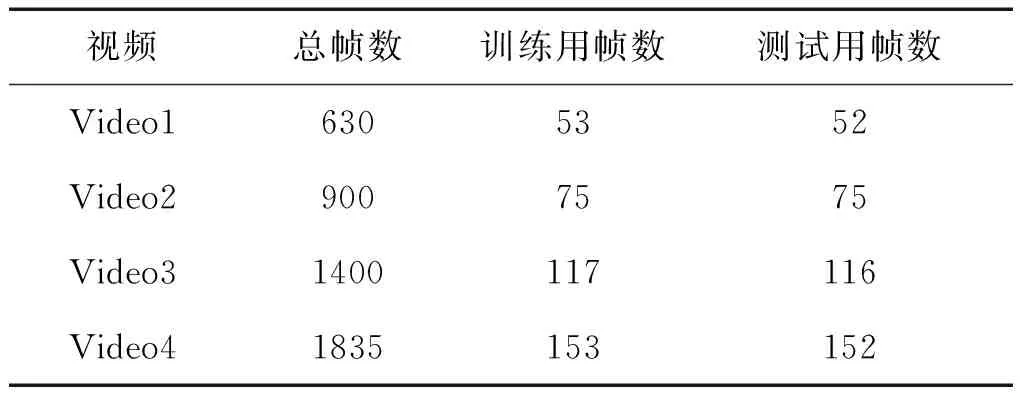
表8 烟雾检测实验数据信息Table 8 Description of smoke detection
将STLCA算法与文献[20]中采用的AdaBoost算法以及文献[5]中的TLNN算法进行烟雾检测,并采用离散余弦变换和离散小波变换2种特征提取方式进行对比试验。在STLCA算法与TLNN算法中近邻数量关系设置为k1=2·k2+1,设置k2=3。在AdaBoost与TLNN算法中,以单特征值训练泛化型AdaBoost的弱分类器,最大训练迭代次数T=30。在STLCA算法求解向量γ值时,设置ε=10-6和δ=10-2,在计算矩阵H时核宽值选择如表9所示。

表9 烟雾检测核宽值Table 9 Kernel width of smoke detection
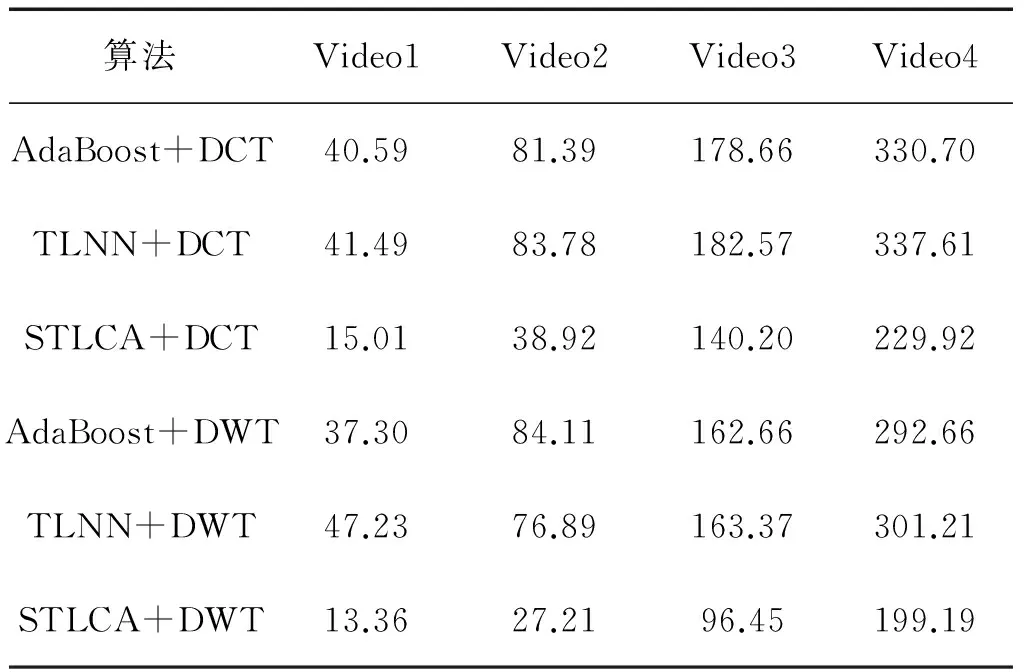
实验通过分类准确率和算法运行时间(训练时间+测试时间)2个方面对算法的效率进行评估,算法运行结果如表10和表11所示。
表10 烟雾检测精度
Table 10 Accuracy of smoke detection %

算法Video1Video2Video3Video4AdaBoost+DCT93.5990.5696.1289.97TLNN+DCT93.4390.0096.2693.70STLCA+DCT95.9193.7896.5696.79AdaBoost+DWT92.7988.1196.9891.56TLNN+DWT93.7588.2296.7793.53STLCA+DWT94.3491.5696.7795.59
表11 烟雾检测运行时间
Table 11 Time-consumed of smoke detection s
算法Video1Video2Video3Video4AdaBoost+DCT40.5981.39178.66330.70TLNN+DCT41.4983.78182.57337.61STLCA+DCT15.0138.92140.20229.92AdaBoost+DWT37.3084.11162.66292.66TLNN+DWT47.2376.89163.37301.21STLCA+DWT13.3627.2196.45199.19
表10和表11分别为AdaBoost、TLNN和STLCA算法并结合离散余弦变换和离散小波变换2种方式进行实验,从检测精度和运行时间2个方面得到的实验结果。从实验结果看,4组视频中采用离散余弦变换进行特征提取检测烟雾时, STLCA在4组数据中都取得了最优的结果,在采用离散小波变换进行特征提取进行烟雾检测时,除Video3外在其余3组视频中取得最优结果。从整体实验结果看,STLCA算法在Video1、Video2和Video4等3组视频数据中取得最优结果,在Video3数据中,虽然未取得最优结果,但STLCA算法结合离散小波变换方式检测结果与最优结果非常接近。在时间效率方面,由于AdaBoost与TLNN算法在弱分类器训练时需要多次对训练集进行遍历,时间效率较低。采用STLCA算法进行视频烟雾检测,由于以稀疏贝叶斯方式为基础,使训练时间大幅减小,无论采用离散余弦变换或者离散小波变换,STLCA算法的时间效率都明显优于其他2种算法。因此STLCA算法有明显的优势。
3 结束语
文中提出了一种新的在稀疏条件下的2层分类算法(STLCA),先用最近邻算法建立一个局部子空间,这样可以限制稀疏贝叶斯信息提取时过度延伸,然后在STLCA分类器的高层,用稀疏贝叶斯在未标记样本子空间进行信息提取。该方法使用少量核就可以达到很高的分类精度,由于其稀疏性在噪声影响下仍有很好的稳定性,且时间效率高。STLCA算法性能通过在噪声数据以及在视频烟雾检测中的应用得到验证。然而该算法由于需要对矩阵进行运算,在对大量数据组成的矩阵求逆时需要大量内存空间,这也成为制约该算法性能的瓶颈,所以如何提取有效特征对数据矩阵进行压缩,提高运算效率是未来研究的方向。
[1] COVER T M, HART P E. Nearest neighbor pattern classification[J]. IEEE Transactions on Information Theory, 1967, 13(1): 21-27.
[2]GOLDBERGER J, ROWEIS S, HINTON G, et al. Neighborhood components analysis[J]. Advances in Neural Networks, 2005, 16(4): 899-909.
[3]DOMENICONI C, GUNOPULOS D. Adaptive nearest classification using support vector machines[C]// Advances in Neural Information Processing Systems. Boston: MIT Press, 2002: 655-672.
[4]ZHANG Yungang, ZHANG Changshui, ZHANG D. Distance metric learning by knowledge[J].Pattern Recognition, 2004, 37(1): 161-163.
[5]GAO Yunlong, PAN Jinyan, JI Guoli, et al. A novel two-level nearest classification algorithm using an adaptive distance metric[J]. Knowledge Based Systems, 2012, 26: 103-110.
[6]FREUND Y, SCHAPIRE R. A Decision-theoretic generalization of on-line learning and application to boosting[J].Journal of Computer and System Sciences,1997,55(1),119-139.
[7]FREUND Y, SCHAPIRE R. Experiments with a new boosting algorithm[C] //Proc of the 13th International Conference on Machine Learning. Bari, Italy,1996: 14 8-156.
[8]SCHAPIRE R, SINGER Y. Improved boosting algorithms using confidence-rated predictions[J]. Machine Learning, 1999, 37(3): 297-336.
[9]张学工,边肇祺.模式识别:2版[M].北京:清华大学出版社, 2000: 156-158.
[10]FIGUEIREDO M A T. Adaptive sparseness for supervised learning [J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(9): 1150-1159.
[11]KRISHNAPURAM B, HARTEMINK A J, CARIN L, et al. A Bayesian approach to joint feature select and classifier design[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2004, 26(9): 1105-1111.
[12]FIGUEIREDO M A T, JAIN A K. Bayesian learning of sparse classifiers[C]// Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. [s.l.], 2001: 35-41.
[13]张旭东,陈锋,高隽,等.稀疏贝叶斯及其在时间序列预测中的应用[J].控制与决策, 2006, 26(5): 585-588. ZHANG Xudong, CHEN Feng, GAO Jun, et al. Sparse Bayesian and its application to time series forecasting[J]. Control and Decision, 2006, 26(5): 585-588.
[14]TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2001(1): 211-244.
[15]CHEN Juan, HE Yaping, WANG Jian. Multi-feature fusion based fast video flame detection[J]. Building and Environment, 2010, 45(5):1113-1122.
[16]KO B C, KWAK J, NAM J. Wildfire smoke detection using temporal-spatial features and random forest classifiers[J]. Optical Engineering, 2012, 51(1): 1-10.
[17]罗胜,JIANG Yuzheng.视频检测烟雾的研究现状[J].中国图象图形学报,2013,18(10):1225-1236. LUO Sheng, JIANG Yuzheng. State-of-art of video based smoke detection algorithms[J].Journal of Image and Graphics, 2013, 18(10): 1225-1236.
[18]GUBBI J, MARUSIC S, PALANISWAMI M. Smoke detection in video using wavelets and support vector machines
[J]. Fire Safety Journal, 2009, 44(8): 1110-1115.
[19]盛家川.基于小波变换的国画特征提取及分类[J].计算机科学, 2014, 41(2): 317-319. SHENG Jiachuan. Automatic categorization of traditional Chinese paintings based on wavelet transform[J]. Computer Science, 2014, 41(2): 317-319.
[20]WANG Zhijie, BEN Salah , ZHANG Hong. Discrete wavelet transform based steam detection with Adaboost[C] // International Conference on Information and Automation. Shenyang, China, 2012: 542-547.

仝伯兵,男,1989生,硕士研究生,主要研究方向为人工智能与模式识别、数字图像处理。

王士同,男,1964生,教授,博士生导师,主要研究方向为人工智能、模式识别和生物信息。

梅向东,男,1966生,高级工程师,主要研究方向为多媒体及计算机应用。
Sparsity-inspired two-level classification algorithm
TONG Bobing1, WANG Shitong1, MEI Xiangdong2
(1. School of Digital Media, Jiangnan University, Wuxi 214122, China; 2. Zanqi Science Technology Development Co.,Ltd, Changzhou 213000, China)
The selection of distance greatly affects KNN algorithm as it relates to finite samples due to weak generalization and low time efficiency in the previous learning of distance. In this paper, a new sparsity-inspired two-level classification algorithm (STLCA) is proposed. This proposed algorithm is divided into two levels: high and low. It uses Euclidean distance at the low-level to determine an unlabeled sample local subspace and at the high level it uses sparse Bayesian to extract information from subspace. Due to the sparsity in noise conditions, STLCA can have good stability, strong generalization and high time efficiency. The results showed that the STLCA algorithm can achieve better results through the application in noise data and video smoke detection.
parse Bayesian; two-level classification; distance learning; video smoke detection; KNN; finite samples; generalization; time efficiency
2014-07-14.
日期:2015-01-13.
国家自然科学基金资助项目(61170122,61272210);江苏省自然科学基金资助项目(BK2011417);江苏省“333”工程基金资助项目(BRA2011142).
仝伯兵. E-mail:tongbobing@163.com.
10.3969/j.issn.1673-4785.201407019
http://www.cnki.net/kcms/detail/23.1538.TP.20150113.1130.004.html
TP391.4
A
1673-4785(2015)01-0027-10
仝伯兵,王士同,梅向东. 稀疏条件下的两层分类算法[J]. 智能系统学报, 2015, 10(1): 27-36.
英文引用格式:TONG Bobing,WANG Shitong,MEI Xiangdong. Sparsity-inspired two-level classification algorithm[J]. CAAI Transactions on Intelligent Systems, 2015, 10(1):27-36.

