一个新超混沌系统的电路仿真与设计

河南牧业经济学院信息与电子工程系 张坦通

一个新超混沌系统的电路仿真与设计

河南牧业经济学院信息与电子工程系 张坦通

本文在Lorenz混沌系统的基础上构造了一个新超混沌系统，对其进行了动力学性能分析，最后设计了一个与其对应的超混沌系统电路，利用Mulsitim软件进行了仿真与实验分析，验证了系统超混沌行为的存在。

Lorenz混沌系统；动力学性能分析；Mulsitim软件

1 引言

混沌系统具有类随机性、对初始条件敏感性以及长期不可预测性等优越的性能，使其在保密通信、工程科学、社会经济学等领域有着广泛的应用前景，然而超混沌系统是一种尤为特殊的混沌系统，其动力学行为更加复杂，随机性更强，提高了低维混沌系统的通信保密性，为混沌理论应用提供了一个新的研究方向。

目前，还没有一套完整的理论来构造出超混沌系统，只是通过对系统动力学性能的分析，来判断系统的超混沌行为，本文是基于Lorenz混沌系统的动力学方程，通过引入反馈控制项，构造出一个新的超混沌系统，分析了系统的基本动力学特性，利用Mulsitim软件对其进行了电路仿真与设计。

2 一个新的超混沌系统

Lorenz混沌系统：

在Lorenz混沌系统的基础上，引入了一个新的反馈控制量，并对其中的状态变量进行函数变换，构造了一个新的四维自治系统：

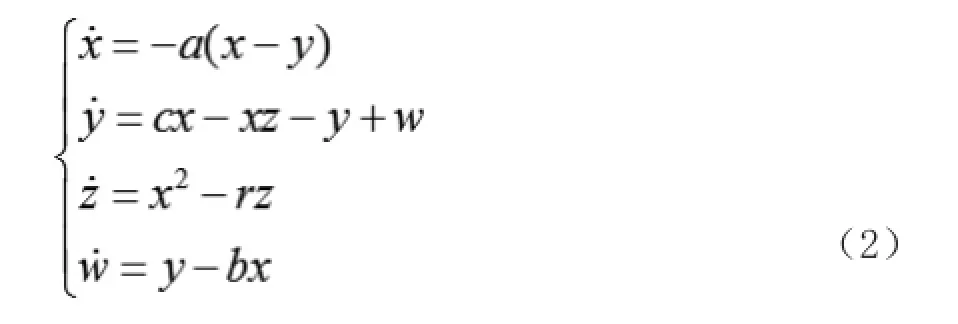
其中x，y，z，w是状态变量；a，c，r的取值与系统（1）相同，即，系统的动力学特性由参数b决定。

判定系统是否存在超混沌现象，需满足三个条件：（1）至少是四维的；（2）具有耗散性；（3）至少存在两个正的Lyapunov 指数，且所有Lyapunov指数之和小于零；首先系统满足条件（1）；其次检验系统的耗散性可通过观察相空间中的一个小体积元变分，而小体积元 V的变分又可以通过流的散度来决定，即：

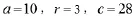
图1 分岔图

通过分岔图可以观察到，b在[3 21]区间变化，系统都能保持两个Lyapunov 指数为正，一个为零，一个为负，且四个指数值之和小于零，满足条件（3），经以上分析，系统（2）存在超混沌现象，在a=10,r=3,c=25,b=8的取值条件下，经matlab软件仿真得到超混沌相图如图2所示。

3 电路的设计与仿真

根据状态方程（2），依据电子线路设计原理，设计了实现超混沌系统（2）的模拟电路，其原理图如图3所示，并在Multisim软件上进行仿真，电路由集成运放构成的加减比例电路、反相电路、积分电路和乘法电路组成，其中乘法器AD633的电压增益为0.1，电源电压值为±15V。

图2 超混沌系统相图

图3 超混沌系统电路原理图

图4 系统仿真相图

经搭建实验电路在Multisim软件仿真获得相图如图4所示，仿真结果与数值分析得到的结果一致，从而验证了系统超混沌行为的存在，这不仅有利于超混沌系统的理论研究，也为其在工程应用领域提供了重要的参考。

4 结论

本文在Lorenz混沌系统的基础上构造了一个新的四维自治系统，经过对该系统动力学特性进行分析，以及在Multisim软件上的电路仿真，验证了超混沌系统的有效性和正确性，本文构造的超混沌系统，电路结构简单且动力学行为复杂，在电子检测、保密通信等领域具有潜在的应用价值。

[1]Lorenz E N．Deterministic nonperiodic flow[J]．JAtmos．Science,1963,20(2): 3130-141．

[2]郭丽颖．基于Multisim的彩灯循环闪烁电路设计与仿真[J]．实验室研究与探索,2010,29(7):187-189．

[3]周小勇．一个新混沌系统及其电路仿真[J]．物理学报,2012,61(3)．

[4]雷腾飞,王清花．一类混沌系统的电路设计及控制[J]．嘉应学院,2014, 32(11): 27-33．

[5]曹永民．赵克奉．胡文亚一个新超混沌系统的数值与电路仿真[J]．电子制作,2015(5)．

张坦通（1983—），男，河南叶县人，河南牧业经济学院信息与电子工程系助教，硕士研究生，研究方向：非线性电路与智能信息处理。