面向监督学习的稀疏平滑岭回归方法*
任维雅,李国辉
(国防科技大学 信息系统与管理学院, 湖南 长沙 410073)
面向监督学习的稀疏平滑岭回归方法*
任维雅,李国辉
(国防科技大学 信息系统与管理学院, 湖南 长沙410073)
摘要:岭回归是监督学习中的一个重要方法,被广泛用于多目标分类和识别。岭回归中一个重要的步骤是定义一个特殊的多变量标签矩阵,以实现对多类别样本的编码。通过将岭回归看作是一种基于图的监督学习方法,拓展了标签矩阵的构造方法。在岭回归的基础之上,进一步考虑投影中维度的平滑性和投影矩阵的稀疏性,提出稀疏平滑岭回归方法。对比一系列经典的监督线性分类算法,发现稀疏平滑岭回归在多个数据集上有着更好的表现。另外,实验表明新的标签矩阵构造方法不会降低原始岭回归方法的表现,同时还可以进一步提升稀疏平滑岭回归方法的性能。
关键词:岭回归;多分类;全局维度平滑性;监督学习
监督学习是机器学习和模式识别中一个重要的学习内容,被应用于包括人脸识别、文本识别及图像分类等诸多领域。在大数据应用需求的背景下,监督学习面临两个重要问题:一是提高分类器的分类准确率问题;二是能够给出对新样本的显式映射,即解决“out-of-sample”问题。
为解决以上两个问题,近年来涌现出一系列基于线性投影的机器学习方法。这些方法包括:基于流形学习的方法,如局部保持投影(Locality Preserving Projections,LPP)[1]和邻域保持嵌入(Neighborhood Preserving Embedded,NPE)[2]等;度量学习(metric learning)方法,如KISS(Keep It Simple and Straightforward)方法[3]、最大边界近邻学习(Large Margin Nearest Neighbor learning,LMNN)[4]和信息论度量学习(Information Theoretic Metric Learning,ITML)[5]等;其他一些著名的机器学习方法,如线性判别分析(Linear Discriminant Analysis,LDA)[6-7]、局部敏感判别分析(Locality Sensitive Discriminant Analysis,LSDA)[8]和间隔判别分析(Marginal Fisher Analysis,MFA)[9]等。
岭回归(Ridge Regression,RR)方法[10-13]是一种利用正则化的最小二乘法方法,最早只设计了单变量标签[11-13]。文献[10]推广了原始岭回归方法,将单变量标签扩展成多变量标签,以解决多分类问题。岭回归方法[10]是一种监督学习方法,由于其出色的学习性能,目前正受到越来越为广泛的关注。它主要包括以下步骤:①生成训练样本点的多变量标签矩阵;②学习线性分类器,即投影矩阵;③对新样本进行分类识别。
文献[10]指出岭回归的多变量标签矩阵方法是特定的。然而,通过将岭回归学习方法纳入基于图(graph-based)的监督学习方法,发现多变量标签矩阵的构造方法是可以灵活设定的,学习投影矩阵的稀疏性往往是一个优良投影矩阵必备的潜在特征。因此在岭回归学习方法中引入投影矩阵的稀疏性约束就得到稀疏平滑岭回归方法。
1岭回归
岭回归方法[10]使用正则单形顶点(regular simplex vertices)[14]作为训练样本的多变量标签,将高维特征空间映射到低维特征空间,并使样本投影到这些正则单形顶点的周围。记训练样本为X=[x1,…,xn]∈Rm×n,对应标签为L=[l1,…,ln],其中li∈{1,2,…,k},代表训练样本共有k个类别。
记Ti∈Rk-1(i=1,2,…,k)为一个正则k单形的顶点,T=[T1,T2,…,Tk]∈R(k-1)×k。T构造方法如下:
1)T1=[1,0,…,0]T且T1,i=-1/(k-1),i=2,…,k。
2)当1≤g≤k-2,有


Ti,g+1=0,g+2≤i≤k-1。
这k个顶点分布在以原点为圆心的超球面上,是k-1维空间中最平衡和对称的分隔点,任意两点之间的距离相等。

岭回归方法最小化如式(1)所示的目标函数:
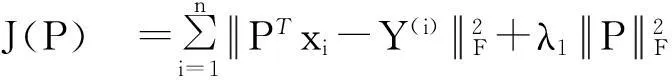
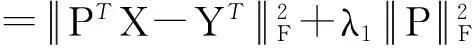
(1)
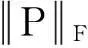
直接求导可得:
P=(XXT+λ1I)-1XY
(2)
式中,I为单位矩阵。

2多变量标签矩阵
岭回归方法实质上是一种基于图的监督线性学习方法,在此基础之上,可以拓展多变量标签矩阵的构造方法。首先考察两个经典的基于图的线性投影算法:局部保持投影LPP[1]和邻域保持嵌入NPE[2]。LPP和NPE优化如式(3)所示的目标函数:

(3)

如果认为具有相同标签的样本是相互相似的,则岭回归学习方法符合基于图的学习方法对于相似样本的约束。实际上,观察式(1),可以发现岭回归的标签矩阵约束了相同标签的样本在投影后的距离,使之趋于接近。另外,不同于LPP和NPP方法,岭回归方法通过标签矩阵的约束避免了解的病态性问题。在LPP和NPP方法中,如果没有正交约束,不同标签的样本在投影后的距离将趋于无穷大;而在岭回归方法中,标签矩阵的约束使得不同标签的样本在投影后的距离将趋于一个固定间隔。
因此,岭回归的多变量标签矩阵只要满足以上对同标签样本的约束和不同标签样本的约束,即可纳入为基于图的监督学习方法。在基于图的监督学习方法的框架下,岭回归的多变量标签矩阵可以通过如下方法构造:
记多变量标签矩阵Y∈Rn×d(d是样本投影后的新维度大小)。岭回归方法[10]使用正则单形顶点,且d=k-1。这种构造方法较为严格,实际上,只需在d维空间中构造k个相互正交、长度为1的顶点就可以满足基于图的学习方法的要求。d的大小是可以定义的,这意味着投影后样本的维度也是可以预先定义的。
标签矩阵的具体构造步骤为:
1)在d维空间中构造k个相互正交、长度为1的顶点,记为T=[T1,T2,…,Tk]∈Rd×k。

根据上述步骤,提出两种构造T的方法:
1)构造方法1:当i=j时,Tij=1,否则Tij=0。要求d≥k,通常可取d=k。
2)构造方法2:在d维空间中生成k个随机顶点,使用施密特正交化方法生成k个新顶点,以构造T。
构造方法1最直观简单,构造方法2可以控制维度。在第五节中将给出不同构造方法对岭回归多分类识别率的影响。
3稀疏平滑岭回归
将所有样本点在维度上的坐标记为一个维度点d(i)(X的第i行),可以使用多种权重[15]度量方法度量其相似性。使用核权重对它们的相似性进行衡量,即如果点d(i)是点d(j)(i≠j)s个最近点之一或点d(j)是点d(i)的s个最近点之一,则:

(4)


将这个假设称为全局维度平滑性假设,其数学的表示为最小化如式(5)所示的正则化项:


=trace(PTDP)-trace(PTWP)
=trace(PTLP)
(5)

考虑正则化项R,岭回归最小化目标变为:
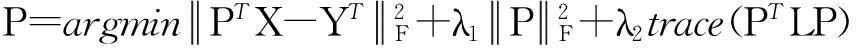
(6)
式中,λ1λ2>0是平衡各正则化项的参数。
比起大多线性学习方法,经典的KISS度量学习方法和MFA方法学习得到的投影矩阵往往具有较好的稀疏性,较好的稀疏度有利于提高投影的鲁棒性,提高模型的泛化能力。因此,进一步对岭回归投影矩阵增加稀疏度要求,式(6)变为最小化如式(7)所示的目标函数:

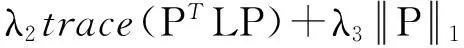
(7)
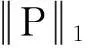
将解决式(7)所示问题(问题(7))的方法称为稀疏平滑岭回归(Sparse smooth Ridge Regression,SRR)方法。
4算法实现
通过变量分别优化的方法解决问题(7),即通过固定其他参数求解某一个参数。采用Inexact ALM[16](augmented Lagrange multiplier)方法,通过一个附属变量拆分目标函数的变量,式(7)可以重写为:

(8)
式(8)的拉格朗日函数为:

(9)
式中,Q是拉格朗日乘子,μ≥0是惩罚参数。
固定其他变量,求P:

(10)
于是,

(11)
固定其他变量,求H:
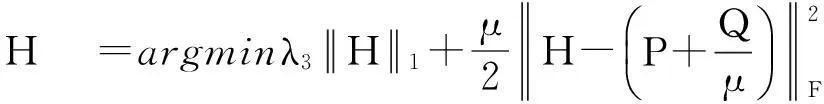
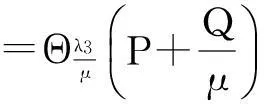
(12)
其中,Θβ(x)=sign(x)max(|x|-β,0)是软阈值操作子[17],且有:

(13)
通过Inexact ALM[16]方法解决问题(7)的完整算法见算法1。

算法1 解决问题(7)的完整算法
5实验
本节面向监督学习进行多分类实验,通过对测试样本的识别准确率来衡量不同算法的水平。实验用的线性投影方法共8种,包括:LPP、NPE、KISS、LSDA、MFA、LDA、RR、SRR。同时,实验分析了不同标签矩阵对岭回归方法的影响。数据集包括图像数据集、人脸数据集、手写体数据集和文本数据集,表1给出了4个数据集的统计指标,图1展示了一些数据集的原始图像示例。
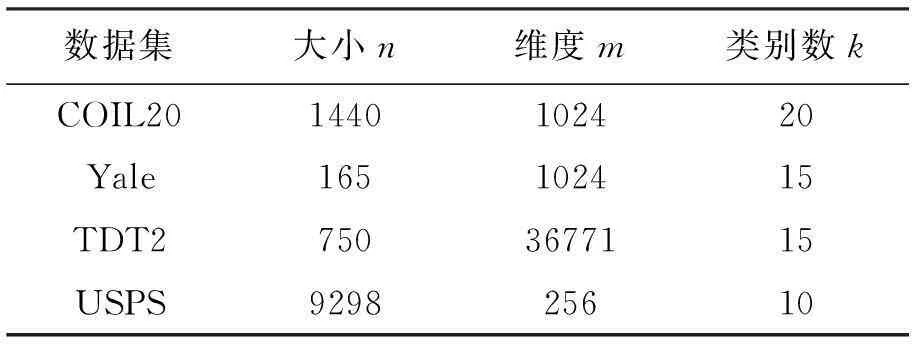
表1 4个数据集的统计指标
5.1 数据集
1)COIL20数据集。COIL20数据集[18]包括20个类别图像,每类图像包含72张不同视角的图像。每张图像降采样后的大小是32×32像素,被表示为一个1024维的向量。
2)Yale数据集。Yale数据集[19]包含15个人物,共165张灰度照片。每个人物有11张表情和外形不同的照片,每张图片降采样后的大小是32×32像素,由一个1024维的向量表示。
3)TDT2数据集。TDT2数据集[20]是一个文本数据集,包括9394个文本文件。每个文本文件被一个36771维的向量表示。样本点最多的前15类数据的各自前50个样本点作为实验数据集使用。
4)USPS数据集。USPS数据集[21]是一个手写体数据集,包括9298张图片,来自10个类别。每张图片大小为16×16像素,由一个256维的向量表示。
通常可采用主成分分析(Principal Component Analysis,PCA)将数据先降维至一个合适的维数以提高运算效率。另外,数据的预处理方法是对数据进行平方和归一化操作。
5.2 实验流程
5.2.1监督分类学习实验
选择一个数据集,确定在每类样本中要挑选的训练样本个数NL,实验流程如下:
1)在每类样本中随机选择NL个样本组成训练集,余下样本作为测试集;
2)用不同方法学习线性投影矩阵;
3)对测试集样本进行投影;
4)通过最近邻方法(1-NN)确定测试样本的预测标签,计算每类方法在测试样本上的识别准确率;
5)重复以上流程50次。
5.2.2标签矩阵实验
构造5个不同的标签矩阵,对比这些标签矩阵对RR和SRR方法的影响。这些标签矩阵包括:

(a)COIL20 (b)Yale

(c) USPS图1 COIL20,YaleB和USPS数据库上的图片示例Fig.1 Sample images in COIL20, Yale and USPS database
1)Y1:原始岭回归构造法[10]。
2)Y2:使用第2节的构造法1,取d=k(d是构造顶点T的维度,k是样本类别数目)。Y2是一个0-1矩阵,每行只有一个1,其余为0。
3)Y3:通过T构造法2构建标签矩阵,令d=2k。
4)Y4:使用T构造法2,令d=3k。
5)Y5:使用T构造法2,令d=m。其中,m是样本数据X的原始维度。
5.3 实验结果
多分类实验结果如表2~5所示。SRR方法在实验数据集上表现良好,特别在TDT2文本数据库和COIL20图像数据库上表现优异。观察USPS数据库和Yale数据库,如表2、表3所示,当训练集数目逐渐增加时,部分经典方法识别效果反而下降,这可能是因为训练出现了过拟合现象。与此同时,SRR方法依然表现良好,体现出较好的泛化能力。
在标签矩阵实验中(见表6),标签矩阵并没有降低RR方法的识别率,这说明将岭回归方法看作是一种基于图的学习方法并由此设计标签矩阵是合理的。这意味着标签矩阵的作用是尽量使投影后的样本同类聚集,异类等距分隔。另外,设计的标签矩阵在SRR方法上比原始标签矩阵有一定的提升,这验证了拓展标签矩阵设计的价值。
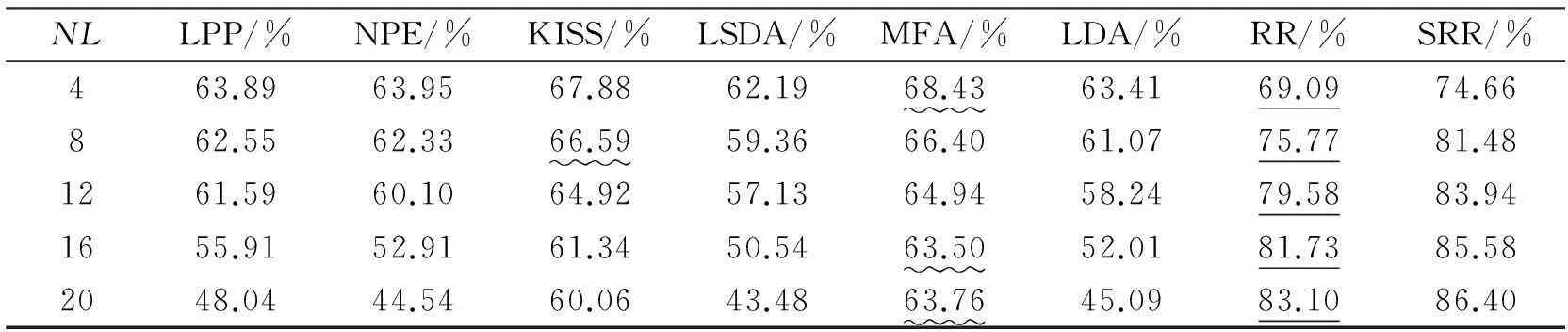
表2 不同方法在USPS数据集上的识别率

表3 不同方法在Yale数据集上的识别率
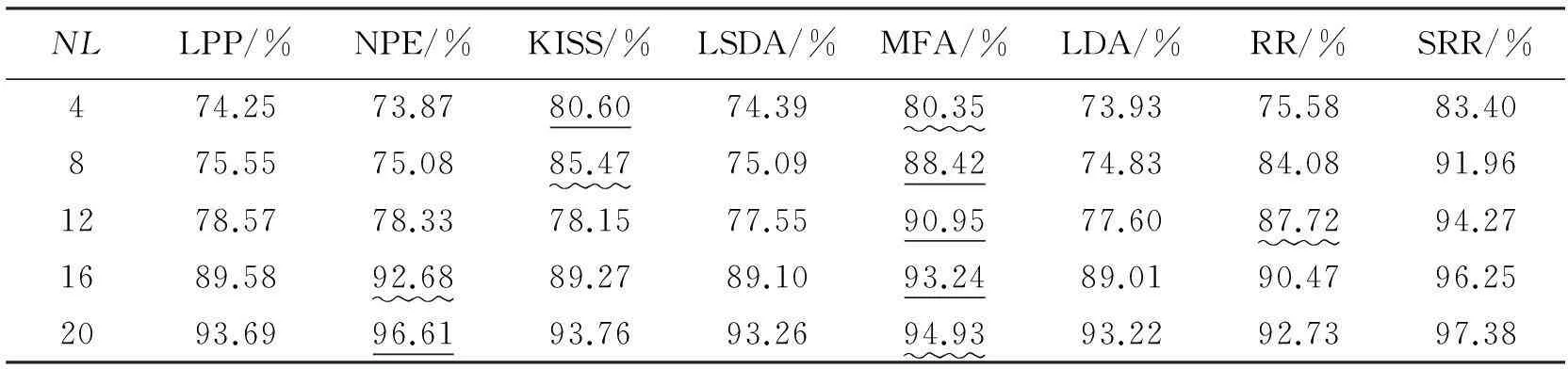
表4 不同方法在COIL20数据集上的识别率

表5 不同方法在TDT2数据集上的识别率
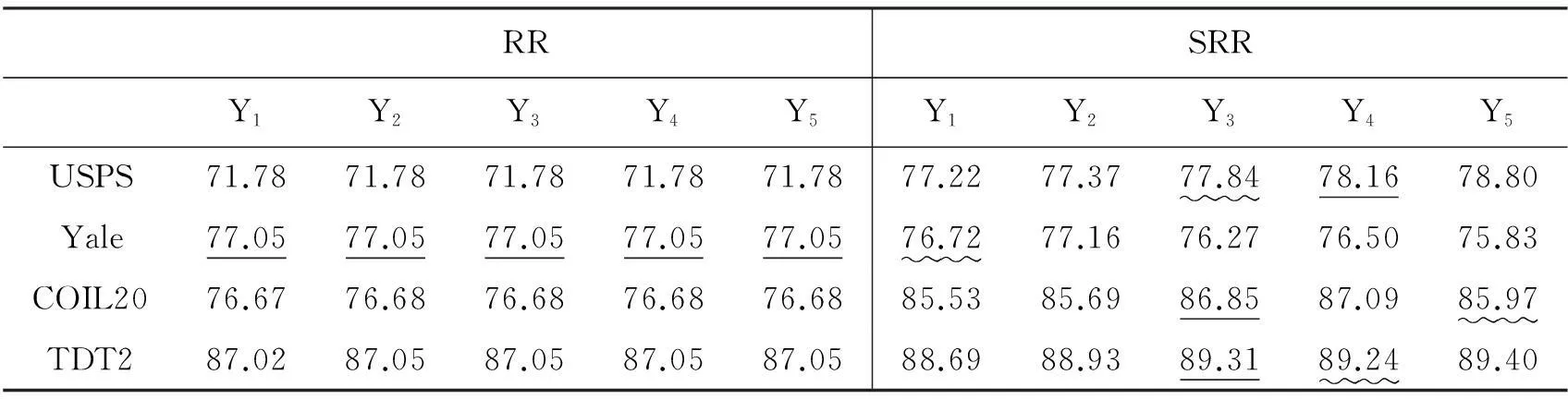
表6 使用不同标签矩阵的岭回归方法在各数据集上的识别率(NL=5)
5.4 算法分析
参数选择是一项重要的工作,文中所使用的对比方法采用其文献所提议的最佳参数。对于SRR方法,可通过有限网格法[22]选择参数。实验采取的参数为:对于USPS,TDT2和Yale数据库,λ1=0.01,λ2=0.01,λ3=0.01;对于COIL20数据库,λ1=0.001,λ2=0.01,λ3=0.1。使用核权重(式(4))来度量维度间的相似度,所有实验取s=5。简单起见,文中使用Y2作为SRR的标签矩阵。
分析表示投影矩阵P的稀疏度,投影矩阵的稀疏度可定义如式(14):

(14)
式中,行向量P(i)的稀疏度sparsity(P(i))可由向量稀疏度[23]计算得到:

(15)
式中,Pij是P(i)的第j个元素。
当一个向量所有值相同时,其稀疏度则为0%,当一个向量只有一个元素不为0时,其稀疏度达到最大,取值为100%。
表7为不同算法得到的投影矩阵的平均稀疏度。由表可看出,SRR方法得到的投影矩阵比RR和其他大多对比方法得到的投影矩阵具有更高的稀疏度。KISS度量学习方法往往可以得到具有最大稀疏度的投影矩阵。对比表2~5和表7,发现投影矩阵稀疏性的提高往往带来识别率上的提升。KISS方法要求相似样本尽量聚集,其对异类样本间的距离没有约束,这可能是其投影矩阵稀疏性高但其识别率不如SRR方法的原因。
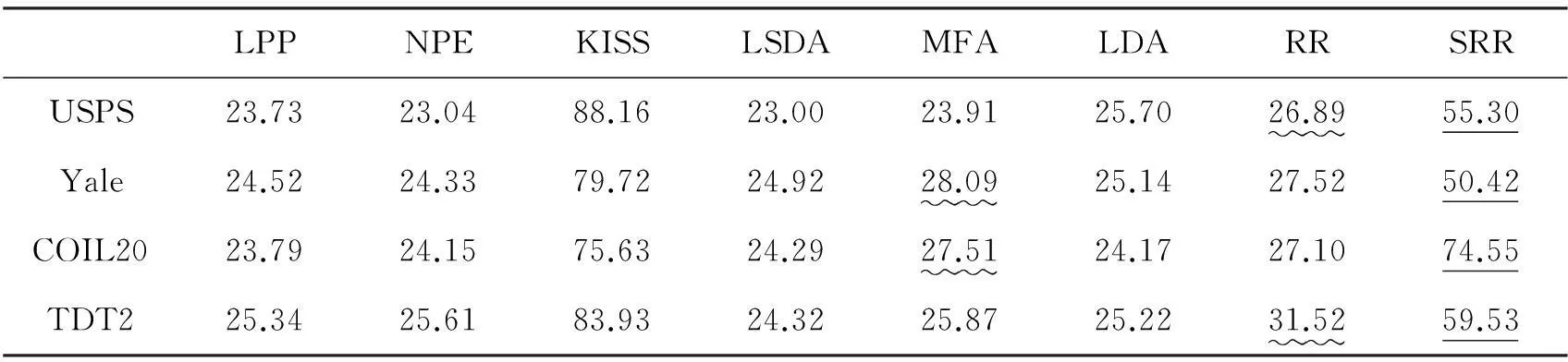
表7 不同算法得到的投影矩阵的平均稀疏度(NL=5)
5.5 稀疏约束拓展
投影矩阵的稀疏性对算法性能有着一定的影响,除了约束外,还可以考察如式(16)所示的正则化项:

(16)


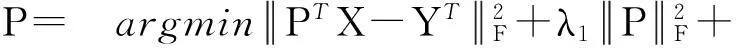

(17)
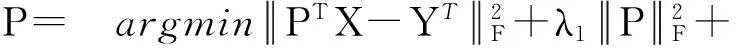
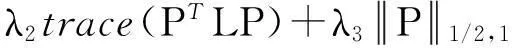
(18)
求解式(17)和式(18)可参考求解式(7)的算法,相应地,只需将式(12)分别替换为式(19)、式(20)。


(19)


(20)
其中,Γ是l2,1范数(行稀疏)操作子(参照文献[28]的列稀疏操作子),Ω是l1/2,1,范数操作子[27]。

表8中列出了SRR系列算法在不同数据库上所达到的识别率和对应的参数值λi(i=1,2,3),其中,参数选择是通过有限网格法[22]进行的,网格值为{0.0001, 0.001, 0.01, 0.1, 1, 10}。就识别率而言,SRR_1,SRR_2和SRR_3表现相近,总体来说,SRR_2表现最好,SRR_1次之,SRR_3最差。
6结论
扩展了岭回归方法中多变量标签矩阵的构造方法,使同类样本在投影后相互聚集,使类别不相同的样本在投影后实现固定间隔分割。通过投影过程中对维度操作的分析,得出全局维度平滑性,同时引入投影矩阵的稀疏性,拓展了RR方法,形成SRR方法。实验分析表明:SRR方法在多个数据集上具有良好的表现,其投影矩阵具有良好的稀疏性,另外,新的标签矩阵构造方法可以进一步提高SRR方法的性能。

表8 不同稀疏约束的SRR方法在4个数据集上的识别率
参考文献(References)
[1]He X F, Niyogi P.Locality preserving projections[J]. Advances in Neural Information Processing Systems, 2004, 16:153-160.
[2]He X F, Cai D, Yan S C, et al. Neighborhood preserving embedding[C]//Proceedings of IEEE International Conference on Computer Vision, 2005:1208-1213.
[3]Koestinger M, Hirzer M, Wohlhart P, et al. Large scale metric learning from equivalence constraints[C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, 2012:2288-2295.
[4]Weinberger K Q, Saul L K. Fast solvers and efficient implementations for distance metric learning[C]//Proceedings of the 25th International Conference on Machine Learning, 2008:1160-1167.
[5]Davis J V, Kulis B, Jain P, et al. Information-theoretic metric learning[C]//Proceedings of the 24th International Conference on Machine Learning, 2007:209-216.
[6]Lu J W, Plataniotis K N, Venetsanopoulos A N. Face recognition using LDA-based algorithms[J]. IEEE Transactions on Neural Networks, 2003, 14(1):195-200.
[7]Welling M. Fisher linear discriminant analysis[J]. Department of Computer Science, 2008, 16(94):237-280.
[8]Cai D, He X F, Zhou K, et al. Locality sensitive discriminant analysis[C]//Proceedings of the 20th International Joint Conference on Artifical Intelligence, 2007:708-713.
[9]Xu D, Yan S C, Tao D C, et al. Marginal fisher analysis and its variants for human gait recognition and content-based image retrieval[J]. IEEE Transactions on Image Processing, 2007, 16(11): 2811-2821.
[10]An S, Liu W Q, Venkatesh S.Face recognition using kernel ridge regression[C]//Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition, 2007:1-7.
[11]Saunders C, Gammerman A, Vovk V. Ridge regression learning algorithm in dual variables[C]// Proceedings of the 15th International Conference on Machine Learning (ICML98), 1998: 515-521.
[12]Hoerl A E, Kennard R W. Ridge regression: applications to nonorthogonal problems[J]. Technometrics, 1970, 12(1):69-82.
[13]Hoerl A E, Kennard R W. Ridge regression: biased estimation for nonorthogonal problems[J]. Technometrics, 1970, 12(1):55-67.
[14]Parks H R, Wills D C. An elementary calculation of the dihedral angle of the regularn-simplex[J]. The American
Mathematical Monthly (Mathematical Association of America), 2002, 109 (8): 756-758.
[15]Ren W Y, Li G H, Tu D, et al. Nonnegative matrix factorization with regularizations[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2014, 4(1): 153-164.
[16]Lin Z, Chen M, Wu L,et al. The augmented Lagrange multiplier method for exact recovery of corrupted low-rank matrices[R]. Technical Report, UILU-ENG-09-2215, 2009.
[17]Candès E J, Li X D, Ma Y,et al. Robust principal component analysis[J]. Journal of the ACM, 2011, 58(3):1-37.
[18]Nene S A, Nayar S K, Murase H. Columbia object image library (COIL-20)[R]. Technical Report CUCS-005-96, 1996.
[19]Belongie S, Kriegman D, Ramamoorthi R. UCSD computer vision[EB/OL].[2014-07-02]. http://vision.ucsd.edu/content/yale-face-database.
[20]Cieri C, Graff D, Liberman M, et al. The TDT-2 text and speech corpus[C]//Proceedings of the DARPA Broadcast News Workshop, 1999: 57-60.
[21]Hull J J. A database for handwritten text recognition research[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(5): 550-554.
[22]Chapelle O, Zien A. Semi-supervised classification by low density separation[C]//Proceedings of the 10th International Workshop on Artificial Intelligence and Statistics,2005:57-64.
[23]Hoyer P O. Non-negative matrix factorization with sparseness constraints[J]. Journal of Machine Learning Research, 2004, 5: 1457-1469.
[24]Vogt J, Roth V. A complete analysis of the I_1, p Group-Lasso[C]//Proceedings of the 29th International Conference on Machine Learning, 2012.
[25]Chartrand R. Exact reconstruction of sparse signals via nonconvex minimization[J]. IEEE Signal Processing Letters, 2007, 14(10):707-710.
[26]Chartrand R, Staneva V. Restricted isometry properties and nonconvex compressive sensing[J]. Inverse Problems, 2008, 24(3):1-14.
[27]Xu Z B, Chang X Y, Xu F M, et al.L1/2regularization:a thresholding representation theory and a fast solver[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(7): 1013-1027.
[28]Liu G C,Lin Z C,Yu Y.Robust subspace segmentation by low-rank representation[C]// Proceedings of the 27th International Conference on Machine Learning, 2010:663-670.
http://journal.nudt.edu.cn
Sparse smooth ridge regression method for supervised learning
RENWeiya,LIGuohui
(College of Information System and Management, National University of Defense Technology, Changsha 410073, China)
Abstract:Ridge regression is an important method in supervised learning. It is wide used in multi-class classification and recognition. An important step in ridge regression is to define a special multivariate label matrix, which is used to encode multi-class samples. By regarding the ridge regression as a supervised learning method based on graph, methods for constructing multivariate label matrix were extended. On the basis of ridge regression, a new method named sparse smooth ridge regression was proposed by considering the global dimension smoothness and the sparseness of the projection matrix. Experiments on several public datasets show that the proposed method performs better than a series of state-of-the-art supervised linear algorithms. Furthermore, experiments show that the proposed label matrix construction methods do not reduce the performance of the original ridge regression. Besides, it can further improve the performance of the proposed sparse smooth ridge regression.
Key words:ridge regression; multi-class classification; global dimension smoothness; supervised learning
中图分类号:TP391
文献标志码:A
文章编号:1001-2486(2015)06-121-08
作者简介:任维雅(1988—),男,河南周口人,博士研究生,E-mail:weiyren.phd@gmail.com;李国辉(通信作者),男,教授,博士,博士生导师,E-mail:gli2010a@163.com
基金项目:国家自然科学基金资助项目(611701586);数学工程与先进计算国家重点实验室开放资助项目(Grant 2013A08)
收稿日期:*2014-12-26
doi:10.11887/j.cn.201506023

