多视图三角化中特征点噪声尺度的自适应估算*
魏迎梅,康 来
(1.国防科技大学 信息系统与管理学院, 湖南 长沙 410073;
2.国防科技大学 信息系统工程重点实验室, 湖南 长沙 410073)
多视图三角化中特征点噪声尺度的自适应估算*
魏迎梅1,康来2
(1.国防科技大学 信息系统与管理学院, 湖南 长沙410073;
2.国防科技大学 信息系统工程重点实验室, 湖南 长沙410073)
摘要:鲁棒性多视图三角化方法通常借助重投影误差经验阈值来剔除图像对应中的错误匹配,该经验阈值的选取直接影响三维重构场景点的数量和精度。在分析图像特征点定位噪声及对极传递几何原理的基础上,建立对极传递过程不确定性的传递模型,提出一种基于核密度估计的最优噪声尺度估算方法,并将该噪声尺度作为多视图三角化中错误匹配筛选的依据。实验结果表明,该方法可以获得准确的噪声尺度估计,从而有效提升多视图三角化方法的三维重构质量。
关键词:多视图三角化;特征点定位;高斯噪声;核密度估计
基于图像的三维重构是计算机视觉的重要研究内容,近年来备受学术界关注而且取得了众多研究成果[1]。作为基于图像三维重构的核心步骤,多视图三角化(multi-view triangulation)的目标是在各相机内、外参数均已知的情况下估计场景的三维结构[2]。理想情况下,三维场景点坐标可以通过计算其在不同视图中视线的交汇点得到。然而,由于特征点定位噪声和图像对应匹配错误在实际图像中总是存在,因此多视图三角化问题不能采用上述简单的方法求解,而是需要借助鲁棒的外点(outlier)剔除方法将错误匹配删除后利用优化技术对三维场景重构结果进行求精[3-8]。
在多视图三维重构中,为消除图像对应中错误匹配对三角化的不利影响,目前有两种比较流行的策略:一类是迭代剔除方法[3];另一类是整体剔除方法[4]。从本质上来说,上述多视图三角化算法均依据重投影误差经验阈值来识别图像对应中的错误匹配,即若重构的三维场景点在某一视图中的投影与相应的图像特征点的欧式距离大于某一阈值时,则认为该图像特征点为错误匹配对应[1-2]。选取较小的重投影误差阈值可以有效剔除匹配错误对应,也可以有效降低重投影误差,但同时也删除了大量匹配正确的图像对应,从而导致正确重构的三维场景点数量下降,同时也会降低多视图三角化结果的精度。因此,为了获得更加客观的三维重构结果,需要准确估计图像特征点定位噪声尺度,在此基础上确定重投影误差阈值作为错误匹配剔除的依据。
1图像特征点定位噪声及对极传递
1.1 特征点定位噪声及其尺度
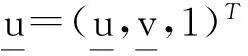
(1)


(2)

图1 高斯噪声下图像特征点位置分布概率密度Fig.1 Probability density of the distribution of image feature point locations under Gaussian noise
1.2 对极传递几何原理
在没有噪声的情况下,假设三维场景点U在三个中心位于O1,O2以及O3的视图中的图像点分别为u,u′以及u″(如图2所示),即:

(3)
根据对极几何原理[2],如下关系成立:

(4)


(5)
其中,符号“≃”表示相差尺度因子的相等。在多视图几何中,上述关系称为对极传递(epipolar transfer)[2]。

图2 三视图对极传递示意图Fig.2 Illustration of three-view epipolar transfer
2自适应特征点定位噪声尺度估算
当变量的观察样本数量较多时,噪声尺度的估计可以采用统计方法[9]。在基于图像的三维重构中,由于所有图像均只成像一次,因此无法使用统计方法。本节推导三视图对极传递不确定性传递模型并提出基于核密度估计的鲁棒性图像特征点定位噪声尺度估计方法。
2.1 对极传递不确定性描述模型
为便于推导,首先定义如下映射:

(6)
其中,[·]3表示取向量的第3维元素的操作。令
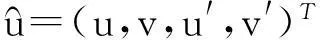
(7)
映射ψ可以表达为如下对极传递映射φ:

(8)
其中,

(9)
与

(10)
定理1[2]:记v为m中均值为μv、协方差矩阵为Σv的随机向量,φ:mn为v附近可微分的映射,则φ(v)∈n是均值为φ(μv)、协方差矩阵为的随机变量(Jφ为映射φ的雅可比矩阵在点μv的取值)。
根据定理1,u″的均值为:

(11)


(12)
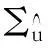

(13)
其中,Jφ为对极传递映射φ(如式(8)所示)的雅可比矩阵在点μu″处的取值。
2.2 噪声尺度估计
本节研究如何利用图像观察值u″,均值μu″以及相应的协方差矩阵Σu″估计特征点定位噪声尺度。为了便于推导,首先介绍如下两个定理。
定理2[2]:记v为m中均值为μv、协方差矩阵为Σv的随机向量,则服从分布。其中,为协方差矩阵Σv的伪逆矩阵,r为矩阵Σv的秩。
定理3[10]:设v为一概率密度函数fv的随机变量,g(·)为单调、可逆且可微分的函数。则z=g(v)的概率密度函数fz为:

上述原理称为变量变换原理。
假设三维场景点在M个视图中可见,记第i(1≤i≤M)个视图中相应的图像观察点为u″i。令:
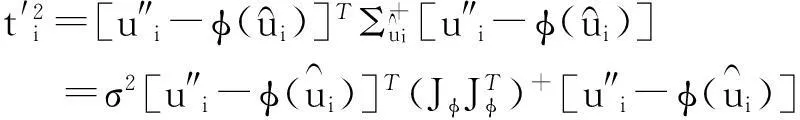
(14)
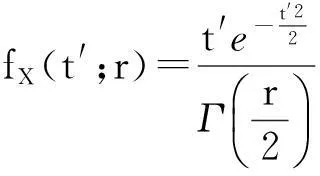
(15)

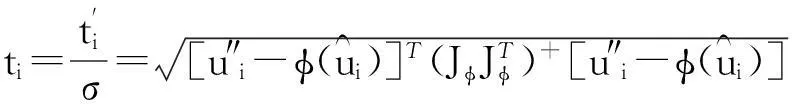
(16)
注意,{ti}仅依赖于图像观察,因此可以从图像特征点对应数据中计算获得。由上述关系以及定理3可知,{ti}的概率密度函数为:
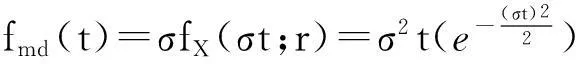
(17)


(18)
因此,噪声尺度估算的关键是定位{ti}分布的密度函数的极大值。对于集合{ti|i=1,…,nσ}(nσ为图像特征点对应三元组数量),使用核密度估计(Kernel Density Estimation, KDE)方法[11]来拟合其分布。在任意位置t,核密度计算如下:

(19)


图3 噪声尺度估算示意图Fig.3 Illustration of noise scale calculation
3实验结果与分析
为验证算法的有效性,利用合成数据和真实图像两种数据对其进行定性和定量测试。该算法的实现采用C++ 语言,所有实验均在Windows XP 操作系统下进行,实验用PC的CPU为Intel Core i7-3770 3.4GHz 处理器,内存为2GB。多视图三角化所需特征点对应采用尺度不变特征转换(Scale Invariant Feature Transform,SIFT)图像特征检测及匹配方法获取[13],错误匹配的剔除采用文献[4]中的方法。上述方法是现有方法中性能最佳的方法之一,不仅能有效删除外点而且可同时获得三维结构的初始估计[5]。在此基础上利用集束优化(bundle adjustment)[14]对重建结果进一步迭代求精。为了定量地分析实验结果,采用模拟数据和具有特殊场景结构的真实图像作为实验数据。
3.1 模拟数据实验
利用模拟数据对对极传递不确定性及噪声尺度估计的精度进行测试。为获取模拟数据,在多个位置上生成虚拟相机同时观察斯坦福大学的bunny点云模型。通过调节相机内、外参数,各相机观察到的图像被限定在1000×1000像素以内。通过改变高斯噪声的标准差,可生成不同噪声尺度的图像数据供测试。
首先,将该协方差计算方法与基于大数定理[9]的统计方法进行对比。对于统计方法,均值Ed[u″]的计算如下:

(20)
其中,Nd为样本数量(取Nd=1500)。协方差Covd[u″]为:
Covd[u″]=Ed[(u″j-Ed[u″])(u″j-Ed[u″])j]
(21)
为了直观地比较协方差估计的优劣,本实验采用k-超椭球(k-hyper-ellipsoid)对协方差进行可视化[9]。对于任意标量k(0≤k≤1),u″位于k-超椭球

(22)

图4 对极传递协方差可视化(σ=2.0像素)Fig.4 Visualization of the covariance of epipolar transfer (σ=2.0 pixel)
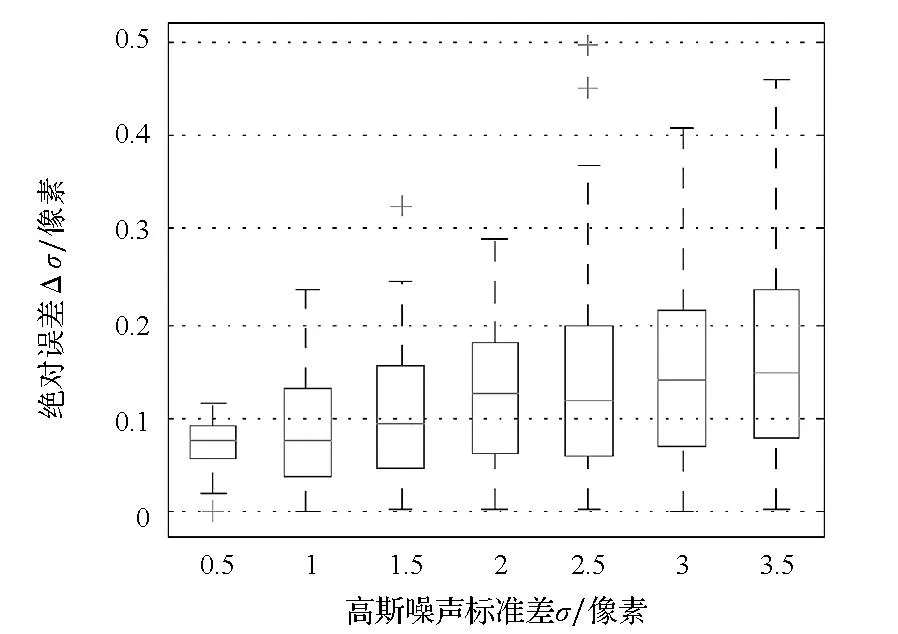
图5 噪声尺度估计精度箱图(外点比例为30%)Fig.5 Boxplot of the accuracy of noise scale estimation (with 30% outliers)
3.2 真实图像实验
对于真实图像,由于无法获取图像特征点定位噪声尺度的真实值,因此无法对噪声尺度估计的精度进行评估。因此,本实验借助场景中的约束来从侧面测试本文方法在真实图像三角化中的性能。图6为本实验采用的真实图像样张,后续定量分析重点考察真实场景中两个便携式电脑屏幕对应的平面区域。
为了考察错误匹配剔除过程中重投影误差阈值选取对三角化结果的影响,本实验利用不同噪声尺度进行处理。三角化重构的最终平面通过最小二乘法拟合三维场景点获得。平面场景三维点重构三维误差定义为重构三维点到拟合平面的最小距离。由于仅考察度量重建,并不关注场景的真实尺寸,因此考察距离的绝对大小并无意义。为了便于比较三维重建精度,将平面区域对应的三维点进行缩放,以确保其包围盒最大边长为100“单位”。同时,本实验考察所有三维点的重投影误差,且上述两个误差度量均计算所有场景点的均方根误差,部分三角化结果如图7所示。其中,图7(a)展示的三角化结果使用的噪声尺度为0.2像素,成功重建的三维点数量约为2400。图7(b)和图7(c)为使用本文自适应噪声尺度的三角化结果的两个视图,成功重建的三维点数量约为10 500。

图7 真实图像三角化结果Fig.7 Results of triangulation on real images
更多的定量对比实验结果如表1所示。实验结果表明,鲁棒性多视图三角化方法采用较小的噪声尺度可以获取较小的重投影误差,但三维重构的精度却并未随之提升。此外,如果采用过小的噪声尺度,会极大地减少成功重建的三维点数量。从表1也可以看出,通过准确的噪声尺度估计,可以有效提升三角化结果的三维精度,而且不会导致成功重建的场景点数量明显减少。

表1 真实图像实验结果对比
4结论
假设图像特征点定位噪声满足高斯噪声分布,在此假设条件下根据对极传递几何原理,推导了三视图对极传递过程中特征点定位不确定性的传递模型,提出一种基于核密度估计的特征点定位噪声尺度估计算法,并将其应用于鲁棒性多视图三角化中错误匹配的识别和剔除。利用仿真数据和真实图像进行实验验证,从定性和定量的实验结果可以看出,该方法估计的噪声尺度具有较高的精度,将自适应噪声尺度作为外点剔除依据有助于提高鲁棒性多视图三角化结果的质量。
在下一步工作中将继续探索在相机内、外参数未知的情况下,特征点定位噪声的估计问题,并研究噪声尺度估计对相机标定及其他多视图几何估计问题(如:相机姿态估计、多视图立体)求解精度的影响。
参考文献(References)
[1]Szeliski R. Computer vision: algorithms and applications[M]. London,UK: Springer, 2010.
[2]Hartley R, Zisserman A. Multiple view geometry in computer vision[M]. 2nd ed.New York,USA: Cambridge University Press, 2004.
[3]Sim K, Hartley R. Removing outliers using theLnorm[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New York, IEEE, 2006: 485-494.
[4]Olsson C, Eriksson A, Hartley R. Outlier removal using duality[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New York, IEEE, 2010: 1450-1457.
[5]Bourmaud G, Megret R. Robust large scale monocular visual SLAM[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New York, IEEE, 2015: 1638-1647.
[6]Li H D. A practical algorithm forLtriangulation with outliers[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), New York, IEEE, 2007: 1-8.
[7]Seo Y, Lee H, Lee S W. Outlier removal by convex optimization forLapproaches[C] //Proceedings of Pacific Rim Symposium on Image and Video Technology (PSIVT), Berlin, Springer, 2009: 203-214.
[8]Ke Q F, Kanade T. Quasiconvex optimization for robust geometric reconstruction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(10): 1834-1847.
[9]Csurka G, Zeller C, Zhang Z Y, et al. Characterizing the uncertainty of the fundamental matrix[J]. Computer Vision and Image Understanding, 1997, 68 (1): 18-36.
[10]Lavine M. Introduction to statistical thought[M]. Tallahassee, USA: Orange Grove Texts Plus, 2009.
[11]Silverman B W. Density estimation: for statistics and data analysis[M].London,UK: Chapman and Hall, 1986.
[12]Wang H Z, Suter D. Robust adaptive-scale parametric model estimation for computer vision[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(11): 1459-1474.
[13]Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110.
[14]Triggs B, Mclauchlan P F, Hartley R I, et al. Bundle adjustment—a modern synthesis[C]//Proceedings of ICCV’99: Proceedings of the International Workshop on Vision Algorithms: Theory and Practice,London, Springer Verlag, 2000: 298-375.
http://journal.nudt.edu.cn
Adaptive estimation of noise scale in feature localization for multi-view triangulation
WEIYingmei1,KANGLai2
(1. College of Information System and Management, National University of Defense Technology, Changsha 410073, China;
2. Science and Technology on Information Systems Engineering Laboratory, National University of Defense Technology, Changsha 410073, China)
Abstract:Robust multi-view triangulation algorithms usually rely on an empirical reprojection error threshold to identify and remove the outliers. The selection of such threshold is critical to both the quantity of successfully reconstructed scene point and its accuracy. Based on the analysis of the noise in feature point localization and the geometry of epipolar transfer, the uncertainty propagation model in epipolar transfer was derived. A novel noise scale estimation approach based on kernel density estimation was proposed and the estimated noise scale was further incorporated into robust state-of-the-art multi-view triangulation algorithm. Experimental results demonstrate that the proposed method is able to obtain accurate estimation of noise scale and to improve the 3D reconstruction quality of multi-view triangulation algorithm significantly.
Key words:image-based 3D reconstruction; feature point localization; Gaussian noise; kernel density estimation
中图分类号:TP391
文献标志码:A
文章编号:1001-2486(2015)06-116-05
作者简介:魏迎梅(1972—),女,甘肃兰州人,教授,博士,硕士生导师,E-mail:weiyingmei126@126.com
基金项目:国家自然科学基金资助项目(61402487)
收稿日期:*2015-01-28
doi:10.11887/j.cn.201506022

