基于精细积分思想的反演简单迭代算法

刘李楠, 殷兴辉, 赵晓萌

(1.海军蚌埠士官学校四系,安徽 蚌埠　233012; 2.河海大学计算机与信息学院,江苏 南京　210098;3.安徽科技学院数理与信息工程学院,安徽 滁州　233100)



基于精细积分思想的反演简单迭代算法

刘李楠1,2, 殷兴辉2, 赵晓萌3

(1.海军蚌埠士官学校四系,安徽 蚌埠233012; 2.河海大学计算机与信息学院,江苏 南京210098;3.安徽科技学院数理与信息工程学院,安徽 滁州233100)

摘要：为了提高走时层析成像中反演算法的性能,采用一种基于精细积分的简单迭代算法。反演计算归结为一个简单的迭代求解过程,对过程中出现的逆矩阵求解利用精细积分思想,确保迭代收敛且能收敛到方程的真解,同时具备较高的迭代速度。检测板模型恢复测试以及实际资料反演结果表明:该方法计算过程简单,在迭代次数较少时即能得到分辨率较高的波速剖面图;与目前常用的一些方法相比,本文方法在反演图像分辨率和迭代效率上都具有一定的优势。

关键词：层析成像;反演算法;简单迭代算法;奇异值分解法;共轭梯度法;精细积分;检测板

人类对地球内部物理性质(如速度、密度、电导率等)以及矿产资源分布的了解,大多来自于可直接观测到的地表地质和地球物理资料的反演和解释,由于地球物理的复杂性和不确定性,使地球物理反问题中存在许多不适定问题及病态方程组,绝大多数的观测数据与模型参数之间都不满足线性关系[1-5]。目前非线性反演方法主要有遗传算法、粒子群算法及神经网络法等,这些方法的计算过程都要花费大量的时间,同时容易受到随机干扰的影响,对稍微复杂的介质分布重建效果较差,所以这些方法现在只能用于解决小型反演问题,尚处于发展研究阶段。

在一定的近似条件下,可将反演过程简化或近似简化为线性关系,把反演算法归结于大型病态线性方程组的求解。有效的线性反演方法主要有:(a)奇异值分解法(SVD法)。该方法是精度较高的算法之一[6-8],缺点是计算速度太慢。(b)联合代数重建算法(SIRT法)。该方法简单、高效,但精度不高[9]。(c)共轭梯度法(LSCG法)[10]。该方法占用内存少,但收敛不规则,与其他线性迭代方法相比,显示出更快的收敛性及更好的可接受结果,是目前常用的反演方法。总体来说,利用LSCG这类迭代算法[11],解序列是最小二乘的意义上收敛的,当连续2次迭代得到的解间距离(某种范数)小于某一预先设定的值时停止迭代,显然这样得到的解序列难以保证收敛到问题的真解。简单迭代算法(SI法)[12]可以解决这个问题,但其中逆矩阵的求解直接影响到计算速度以及精度。本文在一种形式上极为简单的迭代算法基础上,利用精细积分思想[13-15]求解近似逆,同时从理论上证明解序列收敛且收敛到问题的真解,提出一种基于精细积分的简单迭代反演方法(PSI法),并通过理论模型和实际资料反演验证该方法的有效性。

1方 法 原 理

对于线性方程AX=B，利用如下的迭代求解过程:

(A+μI)Xk+1=B+μXk

(1)

上述迭代求解过程可以保证迭代的收敛性,且能收敛到方程的真解。但由于在地球物理反问题中,A多半是接近病态的,因此对矩阵A+μI逆的求解至关重要,将直接影响到迭代算法的精度以及计算速度。常规的高斯等方法求逆矩阵效率不高,下面利用精细积分思想求A+μI的逆矩阵。

在方程AX=B左右两边左乘AT,得

ATAX=ATB

(2)

H(2t)=[I+exp(Qt)]H(t)

(3)

式(3)提供了求矩阵F-1的递推算法,接下来利用精细积分思想,取一个小步长Δt，Hm=H(2mΔt)(m=0,1,...),则

(4)

式中:m——递推矩阵的序数;j——递推序数。

对exp(Q2iΔt)用精细积分法计算,首先对exp(QΔt)进行Taylor展开,由于Δt是极小量,可以只保留前几项,得

(5)

exp(Q2iΔt)=I+Ti(i=1,2,...)

(6)

由式(3)和式(6)得

Hj+1=[I+exp(Q2iΔt)]H0(j=1,2,...)

(7)

当j足够大时,由式(7)即可得到精确的F-1。迭代的过程相当于不断倍增H(t)的积分区域,以2k的指数收敛速度收敛,因此逆矩阵求解计算效率很高。

总结上述分析,归纳出利用精细积分思想的简单迭代反演算法(PSI)步骤如下:

步骤1用规则网格分割成像区域,采用平均速度法获得初始速度模型,利用LTI法正演计算得出矩阵A,建立方程组。

步骤2选定参数μ及小步长Δt,通过式(7)计算等价方程组中ATA+μI的逆矩阵。

步骤3利用式(1)迭代计算出X,即分割后各网格内慢度向量。

步骤4以步骤3中迭代得出慢度值作为新的速度模型,重复步骤1~3,直至迭代结果满足需求。

2数 值 结 果

2.1　理论模型验证

定义相对误差为

(8)

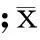
相对误差E越小,表示所得到的估计解越接近于方程的真实解。

待测模型截面宽和深度分别为25 m和80 m,分别给出一个高速异常区和低速异常区,速度分别为1 400 m/s和600 m/s,其他区域速度为1 000 m/s,位置尺寸如图1(a)所示。采用“井间”观测方式,地表左侧井位置坐标为(0,0),

表1　几种方法计算效率比较Table 1　Comparison of computational efficiency of several methods

炮源置于左侧井中,总炮点数为18个,第一个炮点位于深度4 m处,炮点均匀分布、间距为4 m,探测即检波点位于右侧井,检波点数目及深度分布同炮点。

利用规则网格将待测区域离散化,网格尺度选为2.5 m×2 m,将模型区域划分为400个小单元,假设每个小单元格内慢度分布均匀。首先采用LTI法进行正演走时计算,然后分别利用TSVD法、LSCG法及本文方法(PSI法)等进行反演计算,μ值选取0.005,各种算法到达指定精度的计算效率如表1所示。

相对误差越小越好,但并不表示相对误差小的成像效果就一定好,在对算法进行评价时,除了相对误差、计算速度等定量分析,很重要的方面是直接通过反演图像进行定性分析。未加入噪声,以及信噪比为13,分别利用LSCG及PSI两种算法得出反演图像如图1所示(v为射线速度，以下同)。

图1　理论模型及反演结果剖面图Fig.1　Theoretical model and inversion results of velocity profile

可以看出,在没有添加噪声的情况下,2种方法反演成像都能很好地反映异常区域位置及尺寸,说明了这2种方法的有效性。进一步仔细观察发现:本文PSI法描绘出的异常区域位置分布及尺寸更加符合原模型,同时其余区域速度分布更加均匀。在添加噪声后,2种算法反演成像中异常区域都能被反映出来,高速区、低速区均明显可见,但LSCG法成像中出现了一些慢度值与异常区很接近的伪迹,而利用本文PSI算法反演得到的图慢度值与该区域理论值较接近,出现的少量高速干扰不会影响到异常区域的判别,基本真实地反映出模型分布情况。

进一步分析验证方法的有效性,建立检测板速度模型,观测系统同上。在深度方向40 m上下分别设置不同尺寸的速度异常区,低速异常区速度值为1 800 m/s,高速异常区速度值为2 200 m/s,具体分布见图2(a)。

图2　二维模型及其反演结果剖面图Fig.2　Two-dimensional checkerboard model and inversion results of velocity profile

从图2(b)、2(c)可以看出,LSCG反演图中各区的边缘分布不清晰,出现很多交错的分布,导致很难正确分辨出不同的区域介质;PSI法反演图像虽然也有少量层间交错,但总体上边缘分布清晰,迭代次数很少时即能基本如实描绘出不同速度区域分布。

2.2　实际数据计算

根据《河北省抚宁县石门寨镇房庄村采空区井间地震CT成像报告》[16],数据采集采用井间方式进行,使用SWS-A多功能面波仪记录波形,震源采用爆炸震源,电雷管激发,激发点距3 m,接收点距2 m,采样间隔0.25 ms,记录长度256 ms。选取其中2个孔的测量数据,采用平均速度法获得初始速度模型(图3(a)),然后利用PSI法迭代计算30次,得到波速剖面(图3(b))。

图3　实际数据初始速度模型及反演结果剖面图Fig.3　Initial velocity model and real data inversion results of velocity profile

右侧孔在约40 m处堵孔蓄水,40 m以下未做扫描穿透,无法取得该段相应的测试资料,因此波速剖面图下部存在非成像区。成像剖面速度均为2.00 ～5.15 km/s之间,浅层地表(10 m以上)波速较低(2.0～2.9 km/s之间),通常为堆积物与砾卵石层,下部为完整的砂砾岩层,波速值分布在3.35～5.16 km/s之间。基岩部分局部低速带为破碎岩体段或岩溶、裂缝发育区,其最大影响深度在40 m左右,40 m以下未见岩溶、破碎带发育。以上结果表明,利用PSI法成像结果是有效的,其波速图像直观地反映了基岩的完整程度,与风化溶蚀以及破碎带分布等有着良好的对应关系。

3结语

本文提出了一种新的地球物理线性反演算法——基于精细积分思想的简单迭代算法,并给出了算法的具体实现步骤。该算法既可以保证迭代的收敛性、确保能收敛到方程的真解,同时又避免了病态或奇异矩阵求逆带来的精度和计算速度下降,具有不依赖初值、收敛速度快等优点。通过二维检测板恢复测试比较以及实际资料反演,验证了PSI算法的有效性与实用性。

致谢:本文的数据由中国科学院地质与地球物理研究所的赵连锋老师提供,中国石油大学的黄光南博士给予了相关指导和建议,在此感谢他们的热情帮助。

参考文献：

[1] BENZ H M, CHOUST B A, DAWSON P B, et al. Three dimensional P and S wave velocity structure of Redoubt Volcano[J]. Journal of Geophysical Research, 1996, 101(B4): 8111-8128.

[2] HUANG Guangnan, LIU Yang. Variable damping constraint tomography and its application in VSP Data[J]. Applied Geophysics, 2012，9(2):177-185.

[3] NEMETH T, NORMARK E, QING F H. Dynamic smoothing in cross well travel time tomography[J]. Geophysics, 1997,62(1):168-176.

[4] MAURER H, GREEN A G, HOLLIGER K. Full-waveform inversion of cross-hole radar data based on 2-D finite-difference time-domain solutions of Maxwell’s equations[J]. IEEE Transactions on Geo-Science and Remote Sensing, 2007,72(5):53-64.

[5] PIDLISECKY A, HABER E, KNIGHT R. RESINVM3D: a 3D resistivity inversion package[J]. Geophysics, 2007, 72(2): 1-10.

[6] PAIGE C C, SAUNDER M A. Sparse linear equations and least squares problems[J]. ACM Transactions on Mathematical Software, 1982, 8(2):195-209.

[7] LINDE N A, TRYGGYASON J E, HUBBARD S S, et al. Joint inversion of cross hole radar and seismic travel times acquired at the south oyster bacterial transport site[J]. Geophysics, 2008,73(4):39-50.

[8] 顾勇为,归庆明,边少锋. 地球物理反问题中两种正则化方法的比较[J]. 武汉大学学报：信息科学版,2005,30(3):238-241. (GU Yongwei, GUI Qingming, BIAN Shaofeng. Comparison of two kinds of regularization methods in geophysical inverse problem[J]. Journal of Wuhan University：Information Science Edition, 2005,30(3):238-241.(in Chinese))

[9] 曹俊兴,聂在平. 基于物理模型的成像算法评价与SASART成像算法[J]. 成都理工学院学报, 1998,25(4):473-479.(CAO Junxing, NIE Zaiping. Evaluation of imaging algorithm and SASART imaging algorithm based on the physical model[J]. Journal of Chengdu Institute of Science and Technology, 1998, 25(4):473-479. (in Chinese))

[10] SLEIPEN G L, FOKKEMA D R. Bicgstab(L) for linear equations involving unsymmetric matrices with complex spectrum[J].Electronic Trasactions on Numerical Analysis,1993, 1(11):11-32.

[11] RAWLINSONA N, PZAGAYA S, FISHWICHKB S. Seismic tomography: a window into deep Earth[J]. Physics of the Earth and Planetary Interiors, 2010,178(3):101-135.

[12] 毛先进,杨玲英. 病态线性方程组的简单迭代解法[J]. 物探化探计算技术,1999, 21(1):14-18. (MAO Xianjin, YANG Lingying. A simple iterative method for solving ill conditioned linear system of equations[J]. Computing Techniques for Geophysical and Geochemical Exploration,1999, 21(1):14-18. (in Chinese))

[13] 富明慧,张文志. 病态线性方程的精细积分解法[J]. 计算力学学报,2011, 28(4):530-534. (FU Minghui, ZHANG Wenzhi. Precise integration method for solving ill conditioned linear equations[J]. Chinese Journal of Computational Mechanics, 2011,28(4):530-534. (in Chinese))

[14] 张文志,黄培彦. 病态代数系统求解的精细迭代方法[J]. 应用数学和力学, 2013, 34(7):736-741. (ZHANG Wenzhi, HUANG Peiyan. Precise iterative method for solving ill conditioned algebraic system[J]. Applied Mathematics and Mechanics, 2013, 34(7):736-741. (in Chinese))

[15] 杨绿峰,洪斌,高钦,等. 混凝土结构中氯离子扩散分析的精细积分法[J]. 水利水电科技进展,2012, 32(2): 32-36. (YANG Lyufeng, HONG Bin, GAO Qin, et al. Precise integration method for analysis of chloride diffusion in mix soil structure[J]. Progress of Science and Technology of Water Resources, 2012, 32 (2): 32-36. (in Chinese))

[16] 李洪涛,孙党生. 河北省抚宁县石门寨镇房庄村采空区井间地震CT成像报告[R].保定：地矿保定工程勘察院, 2000.

Simple iterative inversion algorithm based on precise integration method

LIU Linan1,2, YIN Xinghui2, ZHAO Xiaomeng3

(1.TheFourthDepartment,BengbuNavalPettyOfficerAcademy,Bengbu233012,China;

2.CollegeofComputerandInformation,HohaiUniversity,Nanjing210098,China;

3.CollegeofMathematics,PhysicsandInformationEngineering,AnhuiScienceand

TechnologyUniversity,Chuzhou233100,China)

Abstract:In order to improve the performance of the inversion algorithm for travel time tomography, a simple iterative algorithm based on the precise integration method was used. The improved algorithm could be considered a simple iterative process. The precise integration method was used to solve the inverse matrix to ensure convergence and obtain the true solution to the equation at a higher speed of iteration. The checkerboard model recovery test and real data inversion results show that the calculation process of the improved algorithm is simple, and the algorithm can obtain the velocity profile with higher resolution and fewer iterations. Compared with some commonly used methods, this algorithm has higher image resolution and greater iteration efficiency.

Key words:tomography; inversion algorithm; simple iterative algorithm; singular value decomposition; conjugate gradient method; precise integration; checkerboard

中图分类号：P631

文献标志码：A

文章编号：1000-1980(2015)06-0594-05

作者简介：刘李楠(1983—),男,安徽六安人,博士研究生,主要从事电磁波及声波层析成像研究。E-mail: linan10241@sina.com

基金项目：安徽省级高校自然科学基金(KJ2012Z 056);安徽科技学院青年基金(ZRC2014442)

收稿日期：2014-12-10

DOI：10.3876/j.issn.1000-1980.2015.06.015