水利测绘中GPS高程拟合的应用

王月恒，黄 江

(中水淮河规划设计研究有限公司，安徽合肥 230000)

水利测绘工作中，平面控制测量随着仪器技术的不断发展、GPS测量技术的广泛使用，工作效率已经大大地提高，然而，高程控制测量仍沿用传统的水准测量方法，屡屡投入大量的人力、物力。D、E级GPS网点应按四等水准测量或与其精度相当的方法进行高程联测［1］，GPS拟合高程测量不失为一个值得探讨的方案。

1 GPS拟合高程测量原理

1．1 高程系统

大地高是由地面点沿通过该点的椭球面法线到椭球面的距离，通常以H表示。利用GPS定位技术，可以精确测量该点在WGS84中的大地高。

正高是由地面点并沿该点的铅垂线至大地水准面的距离，通常以Hg表示。正高是不能精确测定的。

正常高是由地面点沿通过此点的正常重力线到似大地水准面的距离，通常以Hγ表示。正常高同样具有重要的物理意义，广泛应用于水利水电工程、管道和隧道工程建设中，而且可以精确地确定。

正常高系统为中国通用的高程系统，水利工程常用目前1985国家高程基准，采用的就是正常高系统。

1．2 求取正常高的原理

似大地水准面与椭球面之间的高差，称为高程异常，通常以ζ表示。正常高与大地高之间的转换关系为:H=Hγ+ζ。

因此，只要求取高程异常，就可以通过GPS测量得到大地高成果求取正常高。在GPS控制网中选择性地使用水准观测得到部分点(下称已知点)的正常高，求取这些点的高程异常，再通过内插的方式求取其余正常高未知点(下称未知点)的高程异常，就可以由大地高求取未知点的正常高［2］。

用内插方式求取未知点的高程异常可以采用以下几种方式:

1．2．1 等值线图法

绘图人员根据一定密度和精度的已知点参考地形图和重力异常图绘制较为精确的似大地水准面图，然后获取相应坐标上的高程异常。该方法对人员与软硬件的要求较高，使用不方便。

1．2．2 解析法

采用某种规则的数学面来拟合测区的似大地水准面。当这一数学模型建立后，根据网点的位置参数，便可计算测区内任一点的高程异常。常用的拟合方法有以下几种:加权平均法、平面拟合法、二次曲面拟合法、三次样条函数法等，下面主要探讨使用多项式曲面拟合法求取未知点高程异常的方式。

设函数模型为:ζ(x，y)=F(a，x，y)=a0+a1x+a2y+a3x2+a4xy+a5y2。式中 ζ(x，y)为未知点(x，y)处的函数逼近值，即该未知点的高程异常，在已知点i(xi，yi)处 ζ(xi，yi)为已知值，a 为待定参数。由已知点的高程异常ζ(xi，yi)通过最小二乘法求取a后，即可通过方程求取未知点的高程异常ζ(x，y)。当上述公式只取前三项时候，即成为最直观的平面拟合模型ζ(x，y)=F(a，x，y)=a0+a1x+a2y。

一般当已知点数超过6个时采用曲面拟合模型，当已知点数在3～6之间时采用平面拟合模型，在实际工作中，应根据地势起伏变化等地理条件选择最优的拟合模型，从而获取精度最高的拟合结果。

2 工程应用分析

现在选取淮干蚌埠周边某段约30 km长河道范围(主要为平原)内GPS控制网，该区域GPS控制网共计有25座控制点，大部分以四等水准精度观测了正常高，笔者选取其中部分控制点作为已知点在南方GPS商用软件gnssadj中进行高程拟合，求取其余点的正常高(下称GPS高程)，并对比水准观测结果。

2．1 GPS控制网概况

该控制网使用南方S86T动态GPS按照D级GPS精度施测，控制点间距在3～8 km之间，均沿淮河干流布设，测区在南方商用软件gnssadj中进行了平差，各项精度指标满足规范要求。

2．2 高程拟合

先选取该测区范围边缘的控制点作为已知点先后通过平面、曲面拟合方式对其余点进行拟合并比对。

2．2．1 平面拟合

选取6点作为已知点，控制点较为均匀地分布于测区周围，网图如图1:

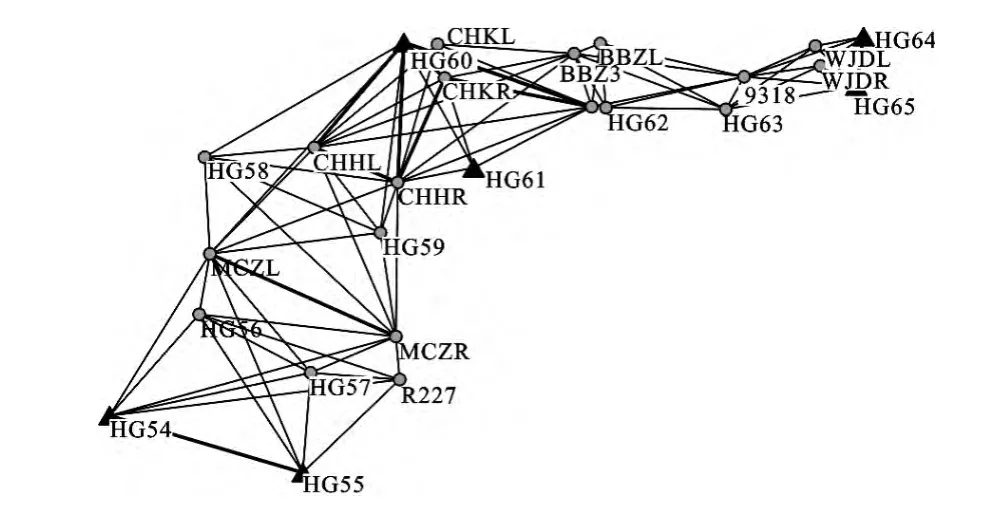
图1 平面拟合点位图Fig．3 Point location pattern of surface fitting

带三角的点为使用的拟合高程点，拟合点19个，结果如表1、表2:

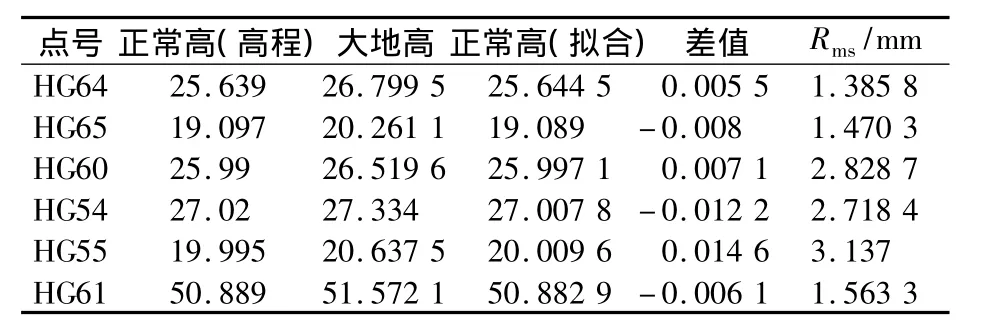
表1 平面拟合残差表Table 1 Residuals of surface fitting

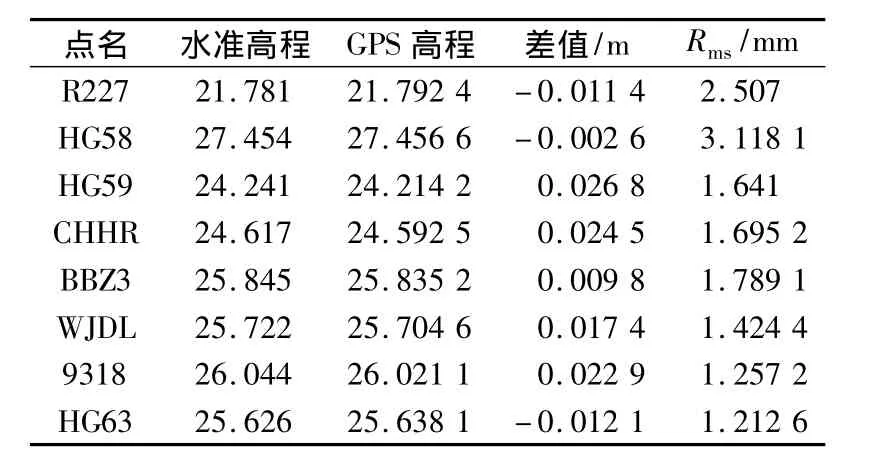
表2 平面拟合高程对比表Table 2 Comparisons of vertical surface fitting

2．2．2 曲面拟合

选取10点作为已知点，控制点较为均匀地分布于测区周围，网图如图2:

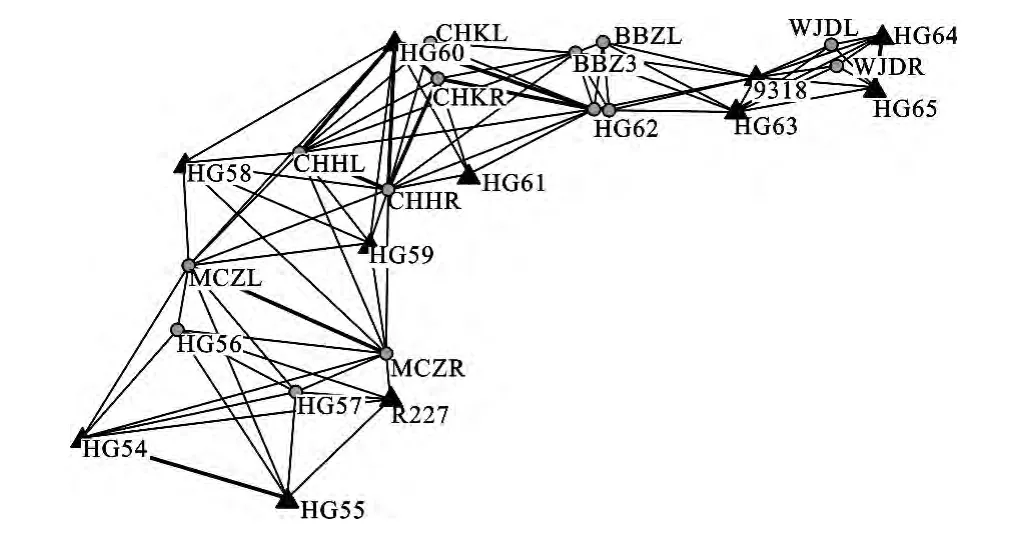
图2 曲面拟合点位图Fig．2 Point location pattern of curve surface

拟合点15个，结果如表3、表4:

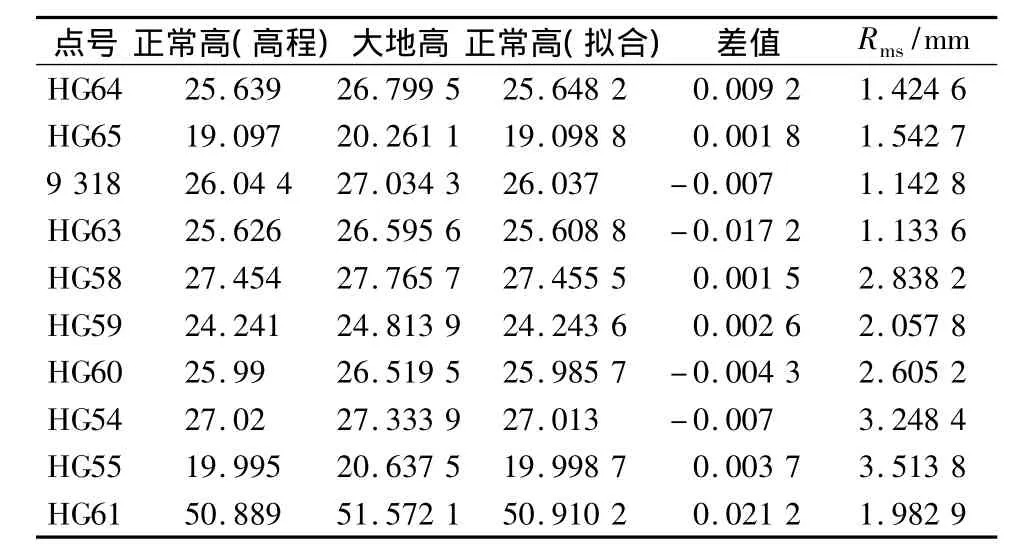
表3 曲面拟合残差表Table 3 Residuals of curve surface fitting

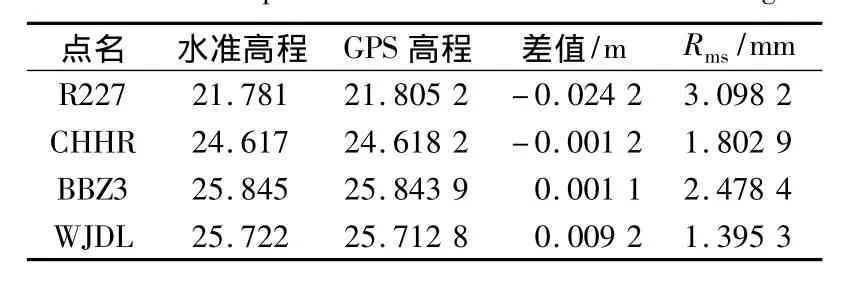
表4 曲面拟合高程对比表Table 4 Comparisons of vertical curve surface fitting

由此可见，根据以上成果对比发现，GPS高程与水准高程差值均在3 cm以内，纵向比较，平面拟合与曲面拟合方式差别不大，局部有轻微差异。

3 精度评定

设水准测量与GPS拟合高程测量分别为往返测，Δ=水准高程-GPS高程，每千米高程测量高程中数的偶然中误差为:

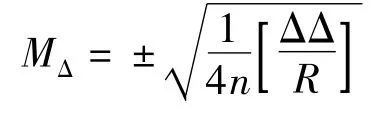
式中:Δ为测段往返测高差不符值(mm);R为测段长度(km);n 为测段数［3］。

根据公式计算得出:在平面拟合条件下，每千米高程测量高程中数的偶然中误差为MΔ=±3．7 mm;在曲面拟合条件下，每千米高程测量高程中数的偶然中误差为 MΔ= ±1．5 mm。

四等水准测量规范中对每千米水准测量高程中数的偶然中误差要求为5 mm，可见以上两种拟合方式的精度均满足要求。

4 结语

从上述工程实例可以看出，在几十千米长度的小范围带状区域，使用GPS高程测量的方式代替传统的水准测量，能够达到四等水准精度，是可行的，根据工作经验，主要应该注意以下几个方面:

(1)GPS控制网中各控制点不宜间距过大，一般不超过10 km，选取的拟合已知点应该均匀地覆盖整个测区。

(2)应根据测区的实际情况选择合适的数学模型，一般较为平坦的区域宜使用平面模型，而起伏较大地区使用曲面拟合模型。

(3)由于GPS测量受到环境影响较大，也包含量取天线高的误差，应保证有一定数量的校核点，确保高程测量的准确性。

［1］ GB/T 18314—2009，全球定位系统(GPS)测量规范［S］．

［2］ 孟凡超，曾旭平．运用GPS水准进行长距离跨河高程传递方法探讨［J］．公路，2007(1):40-41．

［3］ GB/T12898—2009，国家三、四等水准测量规范［S］．