基于DSA的电力调度数字签名方案

郑均辉，甘 泉

（平顶山学院 计算机科学与技术学院，河南 平顶山 467002）

随着信息时代的到来，数字化得到了的深入发展和不断推广。面对电力事业的突飞猛进，人们把改革和发展的目光投向了电力调度系统的开发与研究，如文献[1]针对电力调度的数字化提出了各自的建设思想和实现方法。从现场应用和发表的文献来看，这些电力调度系统都以网络通信为数据传输的基础，已经涉及到数据传输的安全问题。

由于电力行业的特殊性，任何数据传输的安全问题，都将导致灾难性的事故发生，其造成的政治和经济影响是巨大的，带来的损失是不可估量的。文献[2]为了避免在电力调度中心、电厂及用户之间传输的数据被篡改、伪造而产生电力系统事故，提出并设计了认证体系结构。文献[3]分析了电力二次系统所面临的风险，介绍了电力调度系统的证书服务系统及应用。这些方案虽然阐述了能够提高系统安全性的证书服务技术，但是为了存储证书和验证证书的有效性，需要大量的存储空间和计算开销。因此，需要引入一种合适的电力调度系统签名体制。

Al-Riyami等人提出了无证书密码体制，既消除了传统密码体制对证书的需求，也解决了基于身份密码体制中的密钥托管问题，是一种理想的签名方案[4]。在无证书密码系统中用到一个第三方KGC，其作用是负责产生用户的部分私钥。在获得 KGC产生的部分私钥后，用户随机选择一个秘密值，然后用户通过部分私钥和秘密值来产生自己的公钥和私钥，系统将部分公钥绑定同一个身份。一个无证书签名方案由系统参数生成，部分密钥生成，设置秘密值，设置私钥，设置公钥，签名以及签名验证7个算法组成。通常，前两个算法由KGC执行，而其它算法由签名或验证用户执行[5]。由于具有较强的实用性，无证书签名方案的研究受到广泛重视，出现了许多新的方案。但是，这些方案以双线性配对作为设计工具，导致存在计算效率不高的问题[6]。目前无证书密码体制方案已经在电子商务、电子病历等方面开始应用[7]，但在电力调度中的应用研究很少。

鉴于此，本文通过对 DSA签名算法进行改进，构建了一种更有效的基于电力调度系统的无 pairing的无证书签名方案，方案具有抗否认性、抗伪造性、可验证性等特点，能够很好地解决电力调度系统的安全性问题。

1 电力调度系统的安全性分析

电力调度系统通常设计的用户角色为系统管理员、录入操作员、审核操作员、签发操作员等。电力调度系统的控制要依靠生产指令数据及时、准确地进行在这些角色间频繁传送。在电力调度过程中，一般需要解决：数据的不可否认性、数据的不可伪造性、数据签名的可验证性和数据的完整性等问题。

为保证数据传输的安全性，在签名过程中，应涉及有3种对象：

1）信任中心（KGC）：建立公告板，公布共享信息，防止利用公共信息的篡改进行签名的伪造；负责产生用户的部分私钥；如果调度验证者对签名有疑义，可进行判断裁决。

2）调度信息签名者：对传输信息进行签名。

3）调度信息验证者：对传输信息进行验证。

2 基于电力调度系统的DSA无证书签密方案

DSA是 ElGamal、Schnorr等数字签名算法的变体，其安全性基于离散对数问题，是目前公认的安全算法。该算法中没有昂贵的对操作，便于软件和硬件实现，执行效率较高。本文在此算法的基础上，通过分析改进，构建了一种基于电力调度系统的DSA无证书数字签名算法。

系统参数生成：电力调度信任中心输入安全参数k，输出系统主密钥master-key和系统公开参数params。系统公开参数params向电力调度系统中的全体用户公开，而主密钥master-key则由 KGC 秘密保存。 公开参数 params=〈p，q，g，y，H1，H2〉， 其中：p 是一个大的素数，2L-1＜p＜2L，512≤L≤1024，并且按64 bit的幅度递增；q是p-1的素因子，其字长为 160bit；g=h（p-1） /q mod p，h 是一个整数，1＜h＜（p-1），且要求 h （p-1）/q mod p＞1；H1：{0，1}*×Zp*→Zq*，H2：{0，1}*→Zq*。 任意选取 x∈Z q*，计算 y=gx mod p，主密钥是 masterkey=x。

部分密钥生成：设电力调度信息签名者A的身份为IDA，KGC 随机选择 s∈Zq*，计算 w=gsmod p，d=x+sH1（IDA‖w）。d为KGC产生的部分秘钥。d可采用以下方式从KGC传输到 A：A 随机选择 t∈Zq*，计算 j=gt mod p，将 j传给 KGC；KGC 计算 j’=jx mod p mod q，d’=d+s’，将 d’传给 A；A 计算j’=yt mod p mod q，d=d’-j’，从而既可以获取 KGC 产生的部分秘钥d，又可以验证KGC的身份。

设置秘密值：用户随机选取z∈Zq*，计算u=gzmod p，z作为用户A的另一部分私钥，u作用户A的另一部分公钥。

设置私钥：电力调度信息签名者A的私钥为SKA=（，z），私钥由A自己保存。

设置公钥：电力调度信息签名者A的公钥为PKA=（w，u），公钥由KGC在公告板进行告示，防止公钥替换攻击。

签名：设电力调度信息M∈{0，1}*。电力调度信息签名过程如下。

1）生成随机数 k，0＜k＜q；

2）计算 r=（gkmod p） mod q；

3）计算 σ=（k-1（dr+zH2（M））） mod q，（r，σ）即为用户 A对消息M的签名；

4）发送消息和签名结果（M，r，σ） 。

签名验证：验证方收到签名信息M∈{0，1}*以及签名（r，σ），按以下过程进行验证。

1）从KGC处获取电力调度信息签名者A的公钥为PKA=（w，u）及系统公开参数 params；

2）计算 e=σ-1mod q；

3）u1=ywH1（IDA‖w）；

4）u2=uH2（M）；

6）如果 r=v，表示签名有效；否则，签名非法。

3 方案安全性分析

1）可验证性。以上基于 DSA的无证书签名方案中，若签名过程准确无误，则验证等式r=v必然成立。

证明：

针对调度信息签名者和调度信任中心身份，均可采用零知识方式进行认证。若验证者对用户的公钥不信任，可通过以下身份鉴别方案进行验证：验证者随机选择t∈Zq*，将t传给用户；用户计算j=（td+z）mod q，将 j传给验证者；验证者计算 gj=u（ywH1（ID‖w））t，如果相等，则验证通过，否则用户公钥为伪造。

证明：

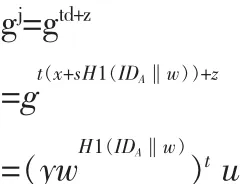
2）不可否认性。签名者发送的私钥中含有了签名者的身份ID，具有不可否认性。

3）不可伪造性。在无证书系统中有两类攻击者，第一类攻击者不知道系统主密钥，但是可以任意替换用户的公钥。第二类攻击者知道系统的主密钥，但是不能替换目标用户的公钥。如果签名方案能抵抗以上两种形式的攻击者，则签名方案为不可伪造性安全的。

对于第一类攻击者，因为不知道系统的主密钥x，所以也不知道用户的部分私钥d。KGC产生的部分私钥d内建立了与用户身份关联的信息，给攻击者设置了第一道壁垒。若攻击者试图替换用户公钥，就必须修改KGC的公告板中的公钥信息，由于公告板是公开的，所以给攻击者设置了第二道壁垒。若KGC或者其它电力调度用户产生怀疑，就会采用零知识方式进行认证。由于攻击者不知道验证者任意选取的t，故攻击者不能构造j。即使攻击者知道验证者选取的t，要求解出j也相当于求解离散对数问题，给攻击者设置了第三道壁垒。故在离散对数问题难解的假设下，该方案可以抵抗第一类攻击的攻击。

对于第二类攻击者，攻击者知道系统的主密钥x，则公钥、部分私钥d以及公开参数对攻击者来说都是已知的。显然，试图通过公钥和部分私钥d直接求解出用户一部分私钥z的做法是不可取的，因为这相当于求解离散对数问题。假设用户伪造一个消息M的签名，就必须绕过部分私钥z，伪造r和 σ，使之满足 r=（（u2）σ-1mod p），这相当于求解离散对数问题。故在离对数问题难解的假设下，该方案可以抵抗第二类攻击者的攻击。

4）数据的完整性。在签名时使用散列函数，能够保证消息的完整性。

本文算法与其他算法在安全性上的比较见表1。（其中，“√”表示“具有”。）其中，文献[3]是基于RSA的证书签名方案，文献[6]是基于双线性对的无证书签名方案。

表1 本文算法与其他算法在安全性上的比较Tab.1 Comparison of security between this paper scheme and other schemes

4 执行效率分析

电力调度系统中数字签名过程中，采用预先计算的方式，在消息M到来之前，先计算出r；当消息M到来时，只需要一次逆运算、一次模运算、一次加法、两次乘法运算、一次散列运算。电力调度系统中数字签名验证过程中，需要一次逆运算、两次乘法运算、四次指数运算、两次模运算、两次散列运算。零知识验证过程中，需要三次乘法运算、三次指数运算、一次模运算、两次散列运算。

根据文献[8]所给出的分析结果，双线性配对、指数运算与散列运算的计算量分别是乘运算的约 21倍、3倍及1倍，相对于标量乘，加法运算、乘法运算、逆运算和模运算均可忽略不计。P表示一个双线性配对运算，S表示标量乘法运算，E表示指数运算，H表示一个散列运算。通过本文算法与其它算法在运算次数的比较（见表 2）可以看出，本文算法的计算量明显小于其他算法，说明本文算法具有较高的运行效率，便于应用到电力调度设备中。其中，文献[3]是基于电力调度的证书签名方案，文献[8]是基于双线性对的无证书签名方案。

表2 本文算法与其他算法在运算次数上的比较Tab.2 Comparison of the number of operations between this paper scheme and other schemes

5 应用测试

本文算法在 VC6.0环境下进行实现，p、q的位数为160位。针对电力调度命令进行签名和验证，以检验本软件的实用性，整个实验采用 Intel酷睿 i5-750，4 G内存的运行环境。密钥和公钥生成过程的平均时间为 1.432 ms，电力调度签名过程消耗的平均时间为 4.31 ms，签名验证过程消耗的平均时间为6.57 ms，零知识验证消耗的平均时间为 4.797 ms。

实验表明该系统具有良好的运行效率，能够满足电力调度的实时性要求。

6 结束语

本文设计了电力调度中的 DSA无证书数字签名方案。方案满足抗否认性、抗伪造性、可验证性和调度消息完整性等安全特性。本文算法与同类签名算法相比，具有较高的运行效率。应用测试表明能够满足电力调度的实时性要求。但是本文算法是以信任中心为研究前提，没有考虑到恶意信任中心，如何设计基于电力调度系统的防止恶意信任中心的无证书签名方案是下一步的研究方向。

[1]高明，袁玲，李文云，等.电力调度系统信息化的几个问题探讨[J].电力系统保护与控制，2011，39（14）:138-142.GAO Ming，YUAN Ling，LI Wen-yun，et al.Study on several problems of power dispatching system information construction[J].Power System Protection and Control，2011，39（14）:138-142.

[2]程旭，梁云，俞俊，等.电力调度分布式工作流设计与实现[J].电力系统自动化，2012，36（21）:93-96.CHENG Xu，LIANG Yun，YU Jun，et al.Design and Implementation of distributed workflow for electric power dispatching[J].Automation of Electric Power Systems，2012，36（21）:93-96.

[3]徐茹枝，郭健，李衍辉，等.智能电网中电力调度数字证书系统[J].中国电力，2011，44（1）:37-40.XU Ru-zhi，GUO Jian，LI Yan-hui，et al.Power dispatching digital certificatesystemin smart grid[J].Electric Power，2011，44（1）:37-40.

[4]李文武，游文霞，王先培.电力系统信息安全研究综述[J].电力系统保护与控制，2011，39（10）:140-147.LI Wen-wu，YOU Wen-xia，WANG Xian-pei.Survey of cyber security research in power system[J].Power System Protection and Control，2011，39（10）:140-147.

[5]Al-Riyami S，Paterson K.C'ertificateless public key cryptography [C]//ASIACRYPT 2003，LNC:S 2894.Springer Verlag，2003:452-473.

[6]Huang X，Susilo W，Mu Y，et al.On the security of a certificateless signature scheme [C]//Proceedings of the CANS 2005.Xia-men， China，2005:13-25.

[7]Yum D H，Lee PJ.Genericconstruction of certificateless signature[C]//Proceedings of ACISP 2004.Sydney， Australia，2004:200-211.

[8]夏峰，杨波.公钥不可替换无证书签名方案[J].计算机科学，2012，39（8）:92-97.XlA Feng，YANG Bo.Certificateless signature scheme without public key replaced[J].Computer Science，2012，39（8）:92-97.