基于泰勒展开式的双二极管模型显示表达

杨桂红，伦淑娴

（1.渤海大学 数理学院，辽宁 锦州 121013；2.渤海大学 新能源学院，辽宁 锦州 121013）

目前，太阳能电池主要有两种模型，即单二极管模型和双二极管模型[1]。这两种模型是关于电流电压特性的数学描述，是隐式超越方程。为了获得不同电压对应的电流值，通常采用数值方法。

然而，即使有相对好的初始猜值，这些数值方法往往难以收敛。因此，在实际的光伏发电系统设计与运行的应用中，设计工程师需要一个简单、快速、有效的太阳能电池显式模型。通常，太阳能电池的显式解析表达方法根据逼近的准确性可以被分为两类。一类是以Lambert W函数为基础的准确的显式表达[2]，但是Lambert W函数方法需要复杂的计算程序以及较长的计算时间；另一类是以初等函数为基础的近似的显式表达[3]。

众所周知，双二极管模型比单二极管模型准确，尤其在低光强条件下[4]。因此，文中提出一个基于泰勒级数展开式的显式双二极管模型。而且，利用制造商提供的标准条件（SRC）下的关键电气参数，建立了该显式模型的两个新的参数提取模型。为了验证提出的显式模型的有效性，本文测试了不同光强、温度条件下不同材料的硅太阳能组件。

1 双二极管太阳能电池模型

双二极管太阳能电池等效电路由一个光生成电流源，两个并联二极管，一个并联电阻和一个串联电阻构成。如图1所示。

根据图1，太阳能电池双二极管模型的I-V特性方程可以写成：

其中，I，V分别是太阳能电池的输出电流和电压，IL是光电流密度，Io1，Io2分别是两个二极管反向饱和电流，Rsh是并联电阻，Rs是串联电阻，a1，a2分别是两个二极管的理想因子参数。这里，，其中，n,n分别是两个二12极管的理想因子，Ns是串联电池的数目，q是电子电荷（1.602 176 46×10-19C），k 是玻尔兹曼常数（1.380 650 3×10-23J/K），T是电池温度（K）。

图1 太阳能电池双二极管电路模型图Fig.1 The two-diode model of solar cells

2 基于泰勒展开的双二极管模型显式表达

式(1)中的指数函数可以采用泰勒级数近似，令x=IRs，即

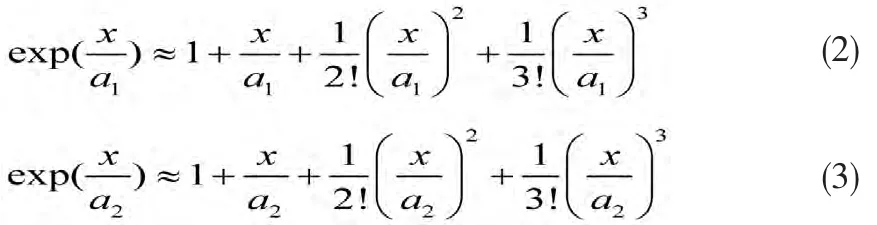
将式(2)，式(3)代入式(1)中，得到

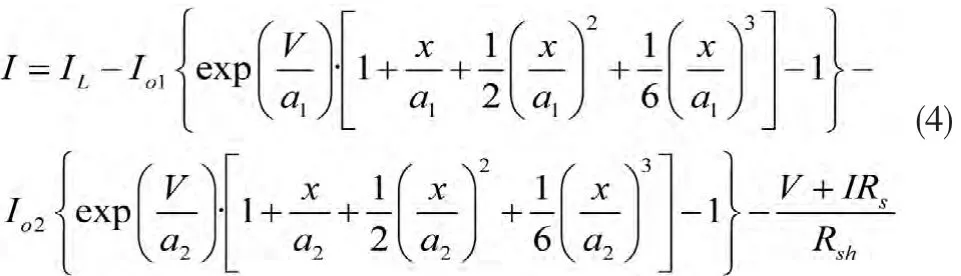
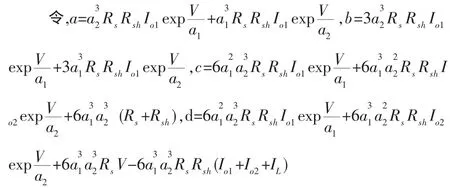
式(4)可以被重新写成：

利用盛金公式[5]，令：

A=b2-3ac，B=bc-9ad，C=c2-3bd，根据式(1)和式(4),得到△=B2-4AC＞0，方程(5)的解为：

因此，电流I的逼近值为：

因此，式(7)是双二极管模型的显式解，根据式(7)可以直接计算太阳能电池的电流值。

为得到（7）中7个电池参数值，本文提出两个基于泰勒展开式的双二极管参数提取模型，这两个新的参数提取模型是基本泰勒展开模型和修正泰勒展开模型。

1)基本泰勒展开模型

根据短路电流在 SRC 下的定义 V=0，I=Isc，ref，因此，式(4)可写成：

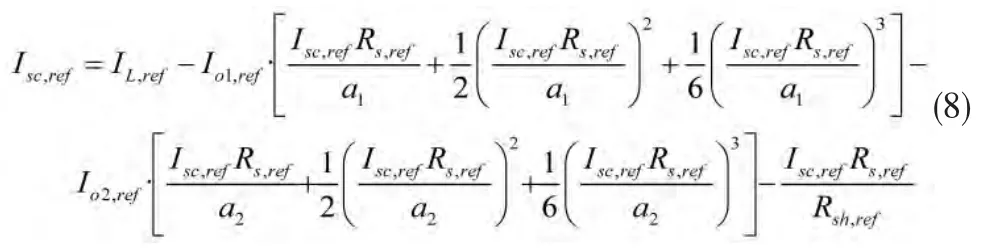
根据开路电压在 SRC 下的定义 I=0，V=Ioc，ref，因此，式(4)可写成：

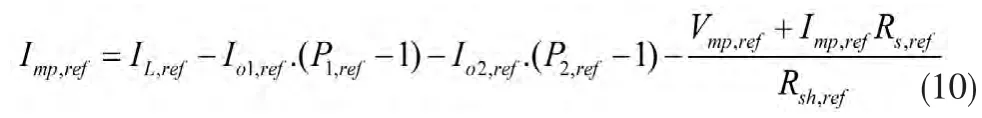
和

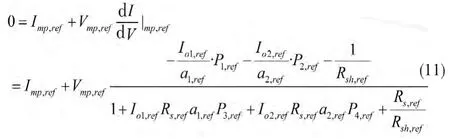
其中

由于4个方程式(8)～(11)不能求解7个未知电池参数，因此利用开路电压温度系数βVoc：

其中，Tref=298 K，Tc=Tref+10 K，βVoc，Te表示温度为 Tc时的开路电压温度系数。通常βVoc由制造商提供，因此能得到βVoc，Te的值。根据式(1)和开路电压定义，得到下面的表达式：

在式(13)中，需要求解，a1，Tc，a2，Tc，IL，Tc，Io1，Tc，Io2，Tc，Rsh，Tc。类似文献[6]中的单二极管五参数模型，提出在不同光强和温度下的，a1，a2，IL，Io1，Io2，Rsh，Rs模型：

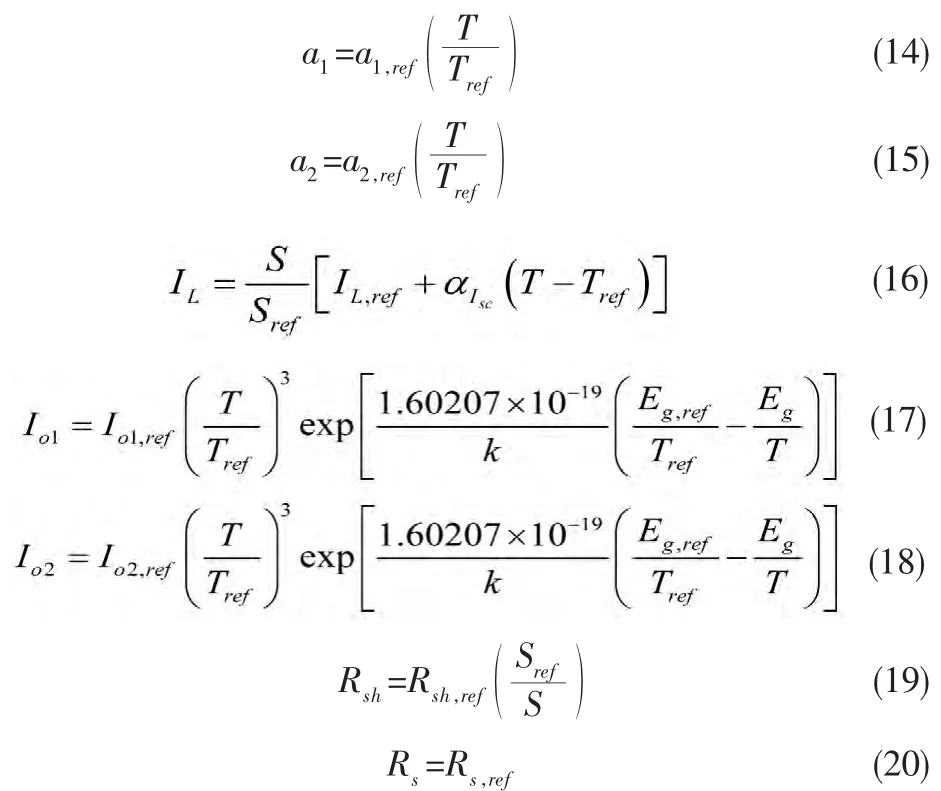
其中 Sref=1 000 W/m2，αIsc是短路电流温度系数，Eg是材料的能带间隙，可以表达为[6]：

其中，对于硅电池 Eg，ref=1.121 eV。

通过增加式(13)得到5个方程求解电池参数。文献[7]中提到，双二极管模型的理想因子n1和n2满足n1+n2≥2.2，由于本文的Ns少于72,因此，假设下面的表达式成立：

现在存在6个方程需求解7个未知的电池参数，因此，需要再增加一个方程。本文令Io2，ref=Io2，ref,guess作为已知参数值，这里Io2，ref,guess是初始猜值，表达式如下：

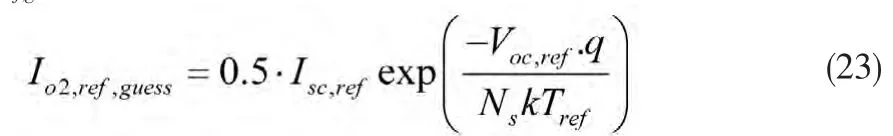
因此利用 6 个方程，即式（8），式（9），式（10），式（11），式（13），式（22）来获得其他6个电池参数。综上所述，通过使用式（14）～（21）能够得到不同光强、温度条件下的电池参数。根据式（8）～（11），去掉下角标“ref”时，能够得到不同光强、温度条件下的 Isc，Voc，Vmp和 Imp。

上面的方法被称为基本泰勒展开模型（BTEM），通过使用BTEM可以得到电池参数。因此，当电池参数值代入方程（4）才真正的得到一个显式的I-V特性模型。

2)修正泰勒展开模型

通常I-V特性曲线用来估计太阳能电池的最大功率，尽管BTEM能够很好地表达太阳能电池的I-V特性曲线，但是在最大功率点处存在较大的模型误差。为了减小最大功率点处的误差，式(10)，式(11)，被修正为：

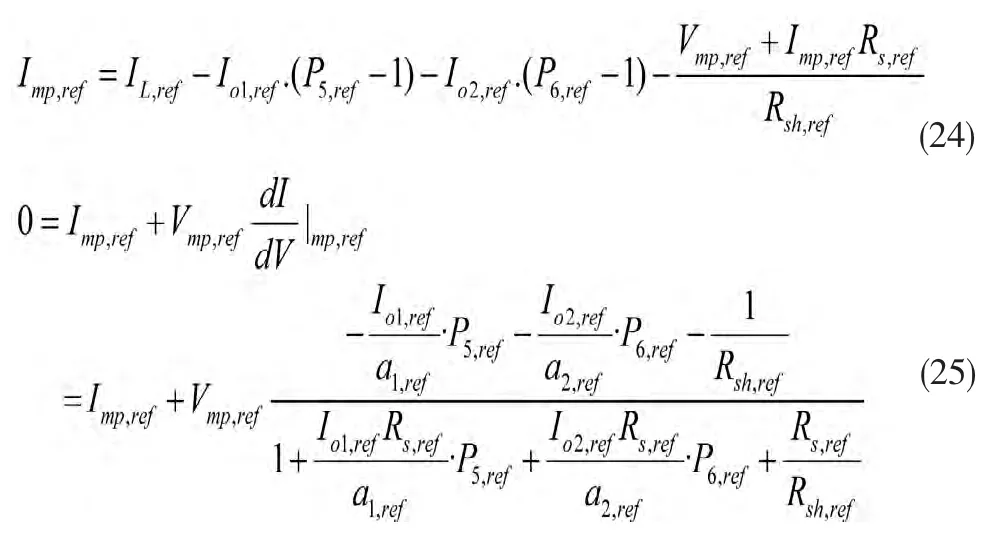
其中

上面的方法被称为修正泰勒展开模型（MTEM）。由BTEM到 MTEM 的转变只是把式(10)，式(11)变成式(24)，式(25)，因此MTEM与BTEM的计算步骤相同。

3 仿真及结果分析

本文使用文献[7]中的实验数据，选择KC200GT和SQ150PC硅太阳能组件验证提出的模型的有效性,两种组件在SRC下的电气参数值由制造商提供，见表1。通过比较本文提出的BTEM和MTEM，文献[7]中的双二极管模型，文献[8]中的双二极管模型，文献[3]中的单二极管模型，验证本文提出的两个模型的准确性。定义均方根误差（RMSE）为：

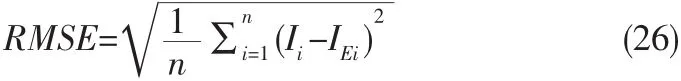
其中Ii是测试模型的电流，IEi是测量数据的电流，n是测量数据的个数。本文测试KC200GT组件的I-V特性见图2和图3。测试SQ150PC组件的I-V特性见图4和图5。另外，分别计算KC200GT组件和SQ150PC组件的RMSEs，见表2。在SRC下，文中提出的BTEM，MTEM和文献[3]中模型计算不同组件的电池参数值,见表3。

表1 标准条件下由制造商数据提供太阳能组件电气参数值Tab.1 Electrical characteristics of solar modules by manufacturer's datasheet at SRC

由图2至图5，通过计算绝对误差可知，BTEM，MTEM，文献[7]模型和文献[3]模型的KC200GT组件的最大绝对误差在光强S=1 000 W/m2，温度T=25℃时分别为0.657 5，0.533 4，0.665 8，0.533 4，文献[8]模型的 KC200GT 组件的最大绝对误差在光强S=1 000 W/m2，温度T=75℃时为1.342 3。以上5个模型的SQ150PC组件的最大绝对误差在光强S=1 000 W/m2，温度 T=60 ℃时分 别为 0.527 0，0.456 2，0.515 3，0.456 4，0.485 1。另外，从表3可以看出MTEM的RMSEs比其他4个模型相对小些。因此，本文提出的两个模型比其他模型更能够准确地逼近I-V特性。

4 结论

本文基于泰勒展开模型获得新的太阳能电池双二极管模

型的显式解析表达[9]。本文呈现的模型能够根据制造商提供的数据直接计算不同电压的电流值。因此，在实际的光伏发电系统设计与运行的应用中，本文提出的模型能够通过直接使用制造商数据快速、准确地估计太阳能组件性能。

表2 不同模型的均方根误差Tab.2 RMSEs of the different models for PV modules

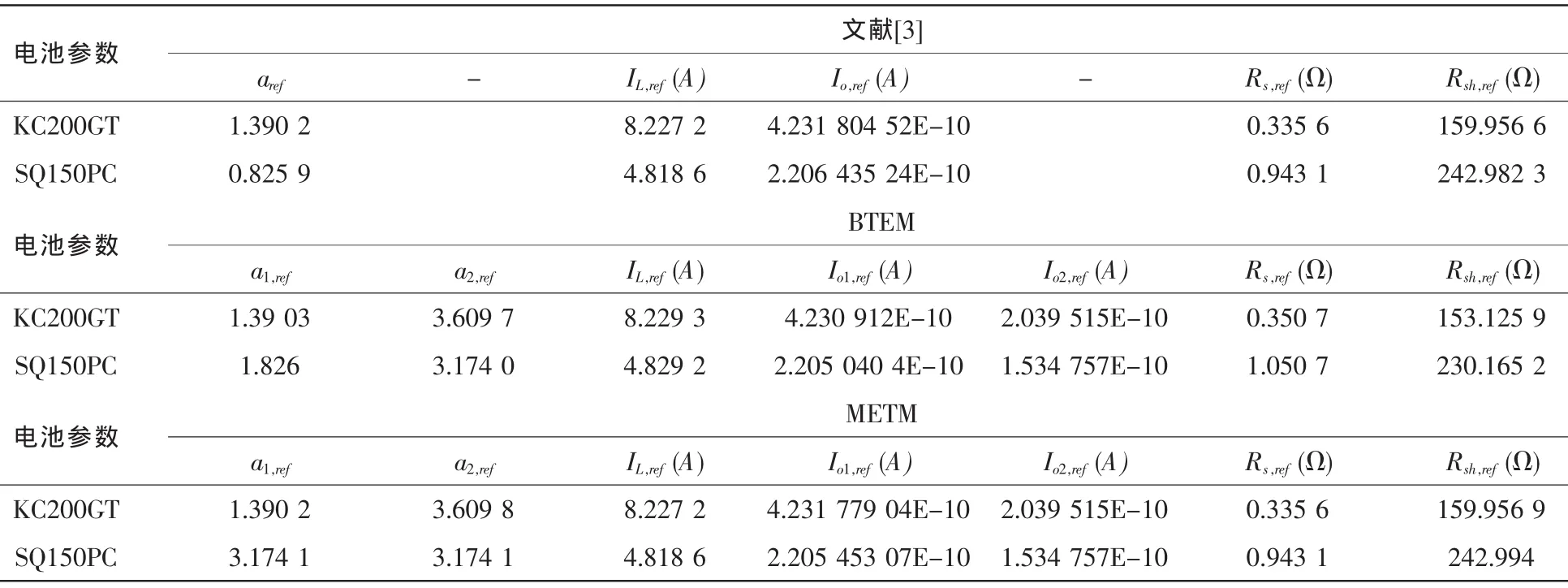
表3 根据制造商数据获得的不同模型电池参数值Tab.3 Cell parameter values of different models obtained by using manufacturer's datasheet

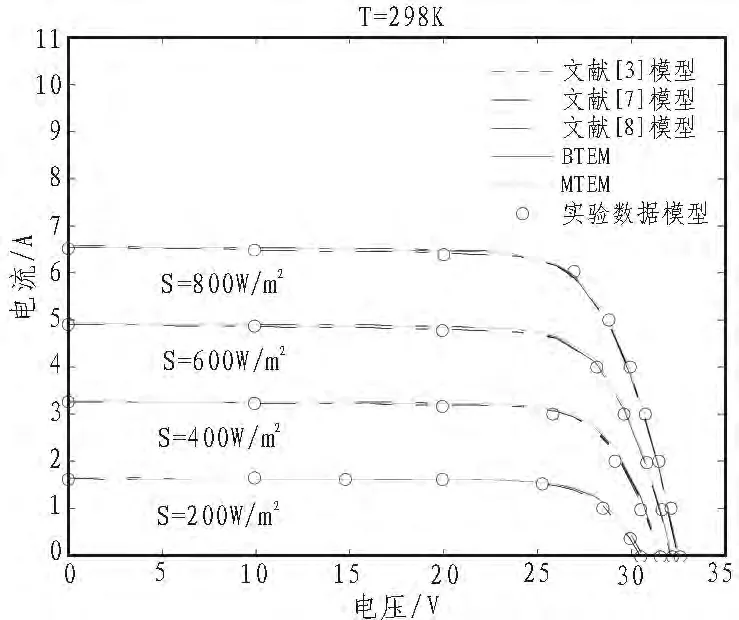
图2 KC200GT温度为25℃时I-V图Fig.2 I-V for KC200GT at T=25℃

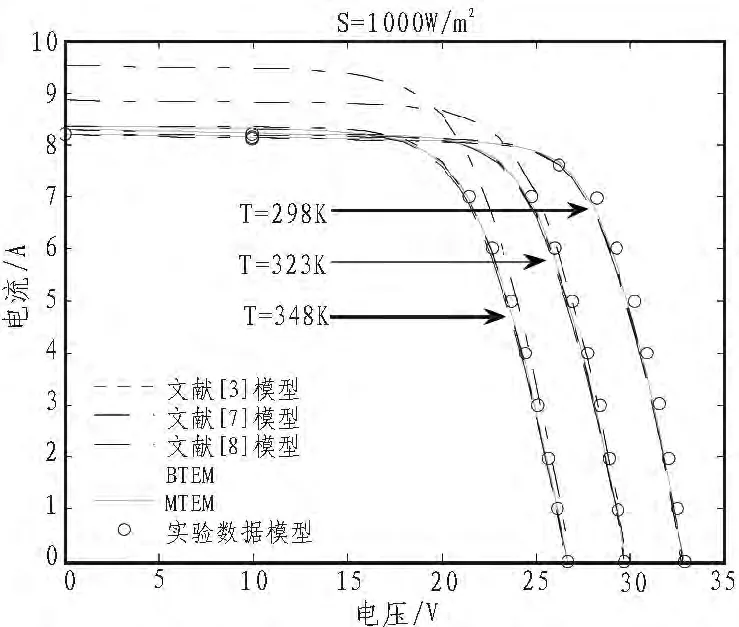
图3 KC200GT光强为1000W/㎡时I-V图Fig.3 I-V for KC200GT at S=1000W/㎡

图4 SQ150PC温度为25℃时I-V图Fig.4 I-V for SQ150PC at T=25℃

图5 SQ150PC光强为1000W/㎡时I-V图Fig.5 I-V for SQ150PC at S=1000W/㎡

[1]Cheknane A,Hilal H S,Djeffal F,et al.An equivalent circuit approach to organic solar cell modeling[J].Microelectronics Journal,2008(39):1173-1180.

[2]Romero B,Del POZO G,ARREDONDO B.Exact analytical solution of a two diode circuit model for organic solar cells showing S-shape using Lambert W-functions[J].Solar Energy,2012(86):3026-3029.

[3]LUN Shu-xian,DU Cun-jiao,GUO Ting-ting,et al.A new explicit I-V model of a solar cell based on Taylor's series expansion[J].Solar Energy,2013(94):221-232.

[4]Kurobe K,Matsunami H.New two-diode model for detailed analysis of multicrystalline silicon solar cells[J].Applied Physics,2005(44):8314-8321.

[5]范盛金.一元三次方程的新求根公式与新判别法[J].海南师范学院学报,1989(2):91-98.

[6]DE SOTO W,Klein S A,Beckman W A.Improvement and validation of a model for photovoltaic array performance[J].Solar Energy,2006,80(1):78-88.

[7]Ishaque K,Salam Z,Taheri H.Simple,fast and accurate two diode model for photovoltaic modules[J].Solar Energy Materials,2011(95):586-594.

[8]Hejri M,Mokhtari H,Azizian M R,et al.On the parameter extraction of a five-parameter double-diode model of photovoltaic cells and modules[J].IEEE Journal of Photovoltaics,2014(4):915-923.

[9]张相华，彭国良，杜太焦，等.一种通用的含热阻温度场计算方法[J].现代应用物理，2015（1）：60-65.