基于MATLAB GUI的振动合成方法的研究
宋 璐,宋燕燕,冯艳平
(1.陕西中医学院 医学技术系,陕西 咸阳 712046;2.解放军信息工程大学 河南 郑州 450001;3.郑州职业技术学院 河南 郑州 450121)
简谐振动的合成,是研究声波、光波和电磁波合成的基础[1],所以它是大学物理教学中一个重要的内容。而在理论教学中,学生很难理解简谐振动的合成过程,需要进行课堂演示。而对于传统的物理演示装置来说,虽然能够直观的显示简谐振动的合成过程,但一般体积较大,精度低,演示内容有限。文献[2]提出了一种采用单片机为核心的简谐振动合成实验仪,利用直接数字合成芯片产生正弦信号,解决了模拟函数频率不准,相位无法确定的问题,但由于成本高,利用率低,不能随时在课堂上演示,应用范围大受限制。文献[3]提出了一种通过计算机模拟实现多种简谐振动合成的方法,改进了传统的演示形式,但由于需要使用C语言编程来实现,对使用者的编程能力要求较高,移植性和可操作性差,参数修改复杂,不利用学生单独操作。
为此,设计了基于MATLAB GUI的程序,不仅能够实现不同种类的多个简谐振动的合成,并且由于引入了基于MATLAB的GUI(图形用户界面),使操作性大大提高,可以任意修改合成类型和振动参数,使得实验结果准确直观,使用方便,可移植性高,有助于学生对各种振动合成的理解。
1 简谐振动合成的基本原理
1.1 同方向同频率简谐振动的合成
假设质点在同一直线上同时进行多个同频率的简谐振动,振动方程为:

其中,i=1,2…n 则合振动方程为[4]:

式中,

分别为振动的振幅和初相位。
由式(2)可知,多个同方向同频率简谐振动可合成为一个同频率的简谐振动,其轨迹为余弦或正弦曲线。
1.2 同方向不同频率简谐振动的合成
如果两个同方向简谐振动的频率不同,利用旋转矢量法分析两个旋转矢量间的夹角或相位差将随时间变化,因而它们的合矢量也将随时间而变化,合振动不再是简谐振动。
当两个同方向的简谐振动频率十分接近时,就会产生拍现象[5],拍频为两个分振动频率之差。
1.3 两个同频率、互相垂直的简谐振动的合成
两个相互垂直同频率的简谐振动合成时,合振动为一椭圆,椭圆的性质由两个分振动的相位差Δφ来决定。如果两个简谐振动的频率之间成整数比,那么它们的合振动就是有一定规律的稳定闭合曲线,称为李萨如图形[6]。
2 MATLAB程序法实现振动的合成
美国MathWorks公司推出的MATLAB是一套具备高性能的数值计算和可视化软件。由于MATLAB可以将矩阵运算、图形显示、信号处理以及数值分析集于一体,构造出的用户环境使用方便、界面友好,因此MATLAB收到众多科研工作者的欢迎[7]。
这里以同方向同频率简谐振动的合成为例,利用MATLAB的.m文件编程实现了振动合成的仿真。假设两路振动参数为:振动1振幅为 1 V,频率100 Hz,初相位 π/6 rad;振动2振幅为2 V,频率100 Hz,初相位π/3 rad,设计的程序如下:

运行后,两个同方向同频率简谐振动的合成结果如图1所示。
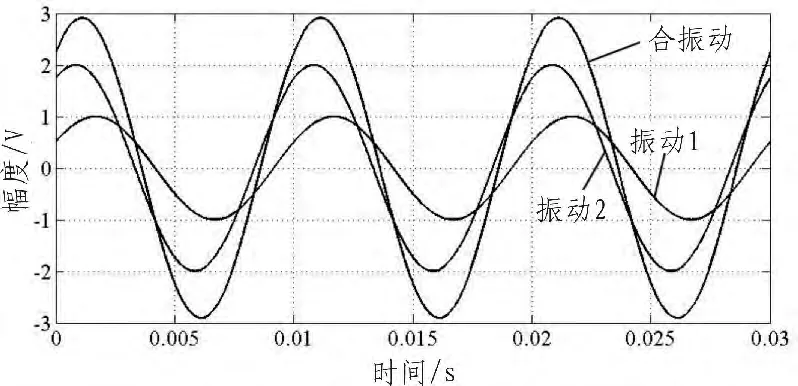
图1 同方向同频率简谐振动的合成Fig.1 Synthesis of harmonic vibration with the same direction and frequency
可以看出,两个同方向同频率简谐振动的合成结果仍然是一个简谐振动。根据计算,得到合振动振幅为2.909 3 V,初相位φ=50.103 9°,与理论计算结果一致。
但当用户需要频繁修改仿真参数时,利用这种方法实现仿真的过程就会变得比较繁琐,并且对于毫无编程经验的学生来说也无法单独完成。所以,如果能开发出基于GUI的图形界面程序的话,无须用户面对复杂的代码,只需输入基本参数,就能实现各种情况下的振动合成,将会是件很有意义的事情。
3 基于GUI的仿真系统的设计
为了能够简化用户操作,方便不熟悉MATLAB的学生使用,采用了基于MATLAB的图形用户界面GUI,通过生成的包含GUI初始化和组件界面布局控制代码M文件,将用户需要的结果显示出来。
3.1 振动合成系统界面设计
在MATLAB的命令窗口输入GUIDE命令或者点击工具栏中的GUIDE图标,打开空白的布局编辑器,选择新建一个默认的.fig文件,根据自己的需要设计GUI界面。设计好的振动合成系统界面如图2所示。

图2 基于GUI的振动合成系统Fig.2 Harmonic vibration synthesis system based on GUI
3.2 仿真结果
首先可以根据需要选择待合成振动的数目和合成模式,再分别输入分振动的各个参数,如果输入有误,可以通过点击数据清空按钮重新输入,若没有问题,可直接点击合成按钮。
选择合振动个数3个,模式为同方向,分别输入三路振动参数如图2所示,点击合成按钮,合成结果如图3所示。
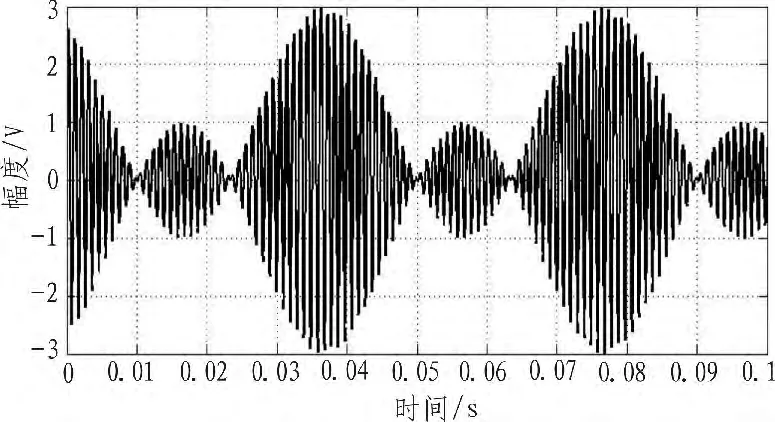
图3 同方向不同频率简谐振动的合成Fig.3 Synthesis of harmonic vibration with the same direction and different frequency
根据图3可以看出,同方向不同频率,但频率相互接近的三路振动合成以后不再是简谐振动,而是出现了拍频现象,与理论分析相符。
或者可以选择合振动个数为2个,合成模式为相互垂直,分别输入两路振动参数,其中振动1振幅为1 V,频率500Hz,初相位 0 rad;振动 2振幅为 1 V,频率 300Hz,初相位0 rad,点击合成按钮,合成的李萨如图形如图4(a)所示;若频率分别改为500 Hz和400 Hz,合成的李萨如图形如图4(b)所示。
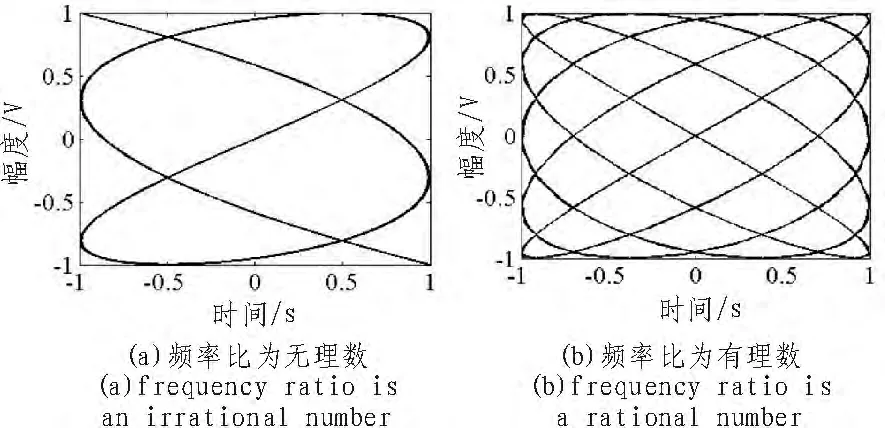
图4 同方向相互垂直简谐振动的合成Fig.4 Synthesis of harmonic vibration with the same direction perpendicular to each other
可以看出,当频率之比为无理数时,其合成的为一不闭合曲线,而当它们的频率之比为有理数时,得到的是一闭合曲线。
其他情况下的仿真过程与上述类似,这里就不再一一赘述了。从以上的分析可以看出,加入了GUI界面的设计后,仿真的操作过程明显得到了简化,振动合成系统效果良好,结果直观清晰。
4 结束语
利用MATLAB作为仿真平台,基于GUI设计的振动合成系统,能够显示不同频率的多个简谐振动的合成,具有形象、生动、直观的特点,使不具备MATLAB知识的学生也可以轻松使用。通过对计算机的操作,易于使用户掌握其具体内容和性质,还可以将理论和实践结合起来,达到加深其理解的目的。
[1]黄贤群.利用计算机软件演示简谐振动的合成[J].韩山师范学院学报,2012,33(6):30-34.
[2]吴俊,张毓麟,晏世雷,等.多倍频简谐振动合成试验仪[J].物理实验,2008,28(7):16-18.
[3]朱云,朱利军,陈健.任意方向简谐振动合成的计算机模拟[J].江苏教育学院学报,2006,23(1):21-24.
[4]蓝海江.多个简谐振动的合成 [J].广西科学院学报,2009,25(1):22-25.
[5]宋璐,冯艳平,卫亚博.基于MATLAB GUI的拍频实现方法的研究[J].大学物理实验,2012,25(3):98-99,114.
[6]候君玲,邵建华,周恭勤.物理学[M].北京:科学出版社,2009.
[7]尹君驰,刘克毅.基于MATLAB的PID控制系统参数调节[J].电子测试,2014,25(3):98-99,114.

