基于修正正态分布的喷泉编码

张茗茗，周 诠

（西安空间无线电技术研究所 空间微波技术国家级重点实验室，陕西 西安 710100）

1998年喷泉码概念由Michael Luby提出，2002年他又提出了第一个实用的喷泉码 LT（Luby Transform）码[1]，在 LT码的基础上，2005年Mohammad Amin Shokrollahi提出了以LDPC码为内码，LT码为外码的级联喷泉码—Raptor码[2]，目前喷泉码的研究已逐渐展开。

喷泉编码因其无码率的特点，在删除信道和低信噪比下的高斯信道中性能优异[3-4]，性能优于LDPC码等传统纠错码，特别适合于互联网的传输和干扰下的无线通信，在深空通信中也有着巨大的潜力，目前已经成为3GPP视频流传输的标准，并在4G通信协议LTE中广泛应用[5]，华为、三星等通信巨头在喷泉编码领域已经申请了大量专利。

由于喷泉编码出现较晚，关于喷泉编码的性能方面有大量的研究，主要分为三类。一类是针对预编码部分的高码率LDPC进行优化，由最初的Gallager的校验矩阵，到后来的Mackay的去四环的校验矩阵和PEG算法的校验矩阵，虽然后来通过非规则码性能有了一点提升，但是在高码率过程中，仍然不可避免的出现四环现象，影响译码效率，在高斯信道中尤为突出[6]。另一类是在初始端再级联一个常规的纠错码，例如扩展汉明码或者RS码[7]，这样性能虽然在有些码率和码长有一些改进，在有些码长还会出现误码率增大的情况，而且还会增加编译码的计算量。最后一种是对LT码进行度分布的优化，LT码的度分布也在针对各种码长进行调整，由ideal到robust再到后来的weaken分布，最近又在码的结构和度分布有大量研究[8-9]，都是为了使编码分组的度分布更为均衡，这样译码效率有所提高，在长码长的情况下，由于大样本使得度分布性能优化不明显，但是短码长差异较大，始终与理想性能有所差距[10]。本文将从原始分组角度，进行度分布的修正规划，使得每一个原始分组对于编译码的贡献趋于一致，避免有些原始分组欠利用和过利用，最终达到较好的译码性能。

1 喷泉编译码的度分布

LT码是喷泉编码的核心，后来为了改善性能将码率0.95-0.9的LDPC码进行级联，由于码率较高，LDPC对于译码的提升有限，LT码起关键作用。当终端接收到的编码数据包的数量略大于K个数据包时，译码器就能够以高概率成功地恢复出发送源数据分组。而度分布决定着LT码码组如何选择，对于编译码有着至关重要的作用。

在LT码的编码中，度是指与编码数据分组相连的源数据分组的个数，如图1所示，s为源数据分组，r为编码数据分组。

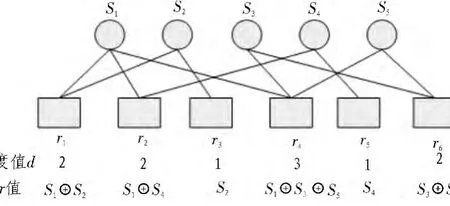
图1 度值示意图Fig.1 Diagram of degree value

如图1所示，给出了LT码的编码过程，编码度分布Ω=（Ω1，Ω2，Ω3，…，Ωk）表示随机选到整数 d 的概率为 Ωd，为了便于数学处理，一般用度分布函数的形式表示为：

度概率分布函数ρ（d）是度即d=i的数据分组在总数据分组中占的比例。

理想孤子分布的随机度生成方法，即随机度按照以下概率分布规律确定：

孤立子分布为了保证每次译码过程中，度为1的集合不为0，为一个固定的值，为了提高译码成功率，Luby提出了一种修正的度分布（Robust Soliton Distribution，RSD）。他首先引入了两个参数c和δ，其中c为一个常数，δ为译码失败概率的上界，并定义

其中，c=0.1，delta（δ）=0.5。

为了简化计算量，Amin Shokrollahi提出 Raptor码，将LDPC码和LT码级联，但是LT码使用弱化的weaken分布，度分布函数满足：

Ω（x）=0.008x+0.494x2+0.166x3+0.076x4+0.083x5+0.056x8+0.037x9+0.056x19+0.025x65+0.003x66（5）

关于3种度分布的关系如图2所示，其中原始码长K为100，编码长度N为200。ideal分布在度为2时达最大值，然后迅速下降，weaken分布在度为20时有一个上升，其它与ideal分布近似，weaken分布只是在固定的几个点有值，其它点处为0。

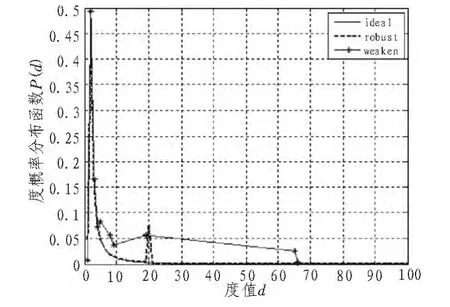
图2 度分布图Fig.2 Diagram of degree distribution

度分布在很大程度上决定译码所需的分组数量，译码过程中实际度值为1的集合一直不为空，在一个恒定的范围，能够保证译码一直进行。

传统的LT编码只对度进行分配，虽然每个编码分组是相互独立的，但是所选择的是哪些原始分组没有考虑，这样导致只注重编码分组对于原始分组如何利用，而对于实际中由于随机选择原始分组给编码带来的贡献差异没有考虑，也没有对于原始分组的分布进行研究。本文将在原有编码基础上提出修正度分布，从原始分组角度进行度的二次选择。

2 本文所提的喷泉编码算法

本文将编码分组作为原始分组，将原始分组作为编码分组，逆向进行统计，得到原始度分布的置信区间，以此作为二次度分配的依据。

2.1 模型建立

假设在LT编码过程中，K个原始分组被编码成N个编码分组，根据度分布 ρ={ρ1，ρ2，…ρs}，其 N 个编码分组相应地

通过度分布被重新划分为 num={num1，num2，…nums}，满足

在逆向过程中，本文建立了ping模型和quan模型，分别进行统计。在ping模型中，对于生成矩阵G（K×N），统计原始分组中参与编码的个数，[1 0 1 1 1]

例如G=0 0 1 1 0，K=3，N=5， 平均统计模型得到0 1 1 0 1 ping=[4，2，3]，即原始分组1被调用了4次，分组2被调用了2次，分组3被调用了3次。

在quan模型中，对于生成矩阵 G（K×N），统计原始分组占该度分布下的权重，在矩阵G（K×N）中，加权统计模型得到quan=[7/3，5/6，11/6]，如表 1 所示。

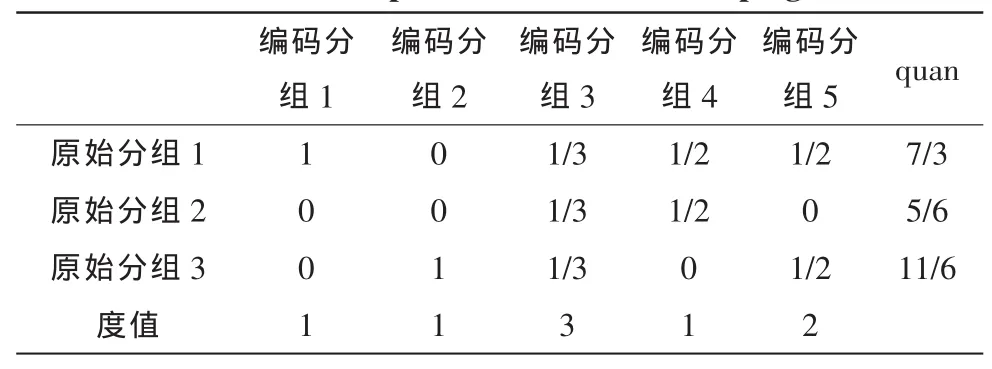
表1 quan模型计算值Tab.1 Com putation value in model ping

ping模型说明被调用的次数，次数越多，说明参与编码的次数多，在译码过程中可以得到的信息源越多，避免局部编码分组出现污染而影响译码的判决。quan模型说明原始分组在编码过程中的影响能力，quan值越大，说明该原始分组起的作用越明显。例如对于编码分组1和2，分别只调用了原始分组1和3，只有原始分组1和3对编码分组1和2起作用，在得到编码分组1和2时，可以很顺利地将原始分组1和3解出，而对于原始分组2，译码起来就显得有些困难，需要得到编码分组1和4的信息才能将其解出。

ping模型适合于高斯信道，能够在低信噪比的情况下正确得到原始信息，但是译码起来需要很多次的迭代，在时间复杂度上开销很大，而且在删除信道下，在迭代过程中存在实际度值为1的集合为空的情况。quan模型适合于删除信道，可以在只获取超过原始分组数目一点的情况下正确译码，但是在删除概率增大的情况下，会出现原始分组没有编码分组对应和起始译码度值为1的集合为空的情况，导致译码失败。

本算法将巧妙结合这两种模型，使得LT码既适合高斯信道也适合删除信道，性能有了明显提升。

2.2 修正分布的阈值确立

在ping模型中，对于每一个编码分组，其度值全部都按照度分布 ρ={ρ1，ρ2，…ρs}的概率选择集合 num={num1，num2，…nums}，模型可以简化为s维伯努利分布函数，而每一个原始分组是从编码分组中均等概率地选择出来。以weaken分布为例，如表2所示。

在ideal、robust和weaken分布中，维度和概率均不相等，但是都满足维度较多，样本较大的情况，这样多维伯努利分布可以简化为正态分布，当编码分组为N时，模型可以认为是N次正态独立事件，其期望为：以weaken分布为例，其期望值为Expectation=

表2 集合与度分布关系表Tab.2 Ralationship between sets and degree distributions

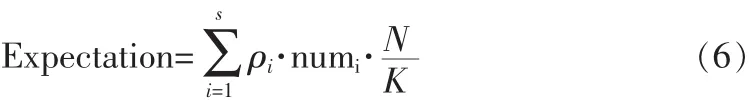
2×5.701 =11.738由于不同的度分布，每个原始分组的ping与期望的偏差pingi-Expectation的绝对值和方差不尽相同，本文采取实验的方法，取K=1 000，N=2 000，对3种分布仿真1 000次进行统计，得到表3所示。

表3 ping模型期望方差表Tab.3 Expectation and variance in model ping

可以看到，3个模型的期望值差别很大，很难有一个统一的标准，标准差差别不大，在3-4之间，所以本文选择3作为ping模型的阈值。

在quan模型中，对于每一个编码分组，首先全部都按照度分布 ρ={ρ1，ρ2，…ρs}的概率选择 num={num1，num2，…nums}选定一个度值numi，如果随机选中原始分组，其quan值为1/numi，模型可以看做是度分布 ρ={ρ1，ρ2，…ρs}的取值为 num={1/num1，1/num2，…1/nums}的 N 次 s维伯努利分布，任意原始分组期望度值为unmi/K，相对于该编码分组的平均度期望Expe_degree=·numi，quan 模 型 中 原 始 分 组 quani=，原始分组中quan模型的期望为：

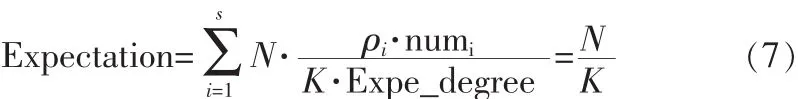
这样对于不同度分布，其quan模型的期望值与度分布没有关系，只与K值和N值有关。但是方差仍然依赖于分布函数，下面是对3种分布的1000次仿真统计，得到表4。

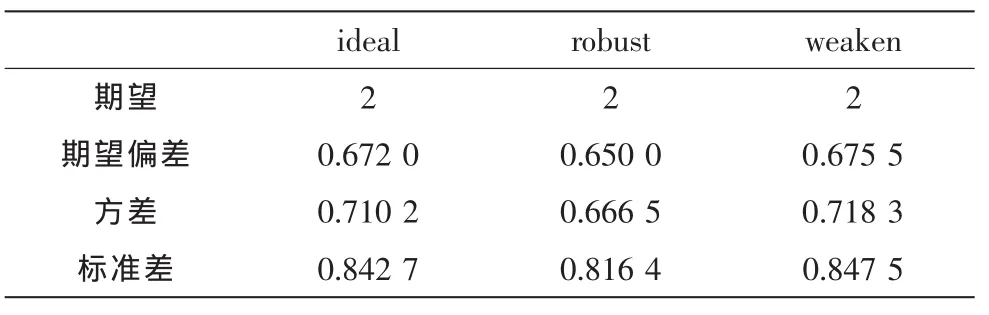
表4 quan模型期望方差表Tab.4 Expectation and variance in model quan

可以看到，在quan模型中，期望值偏差和方差差距都不明显，所以本文以0.7作为quan模型的阈值较为合适。

两个模型和阈值建立起来，首先随机地进行编码，每生成一个编码分组，统计被选中的原始分组的ping值和quan值，当满足条件：

该原始分组被抛弃，在以后的编码过程中不被选择。这样一来，绝大多数的原始分组都落在了Expectation_ping和Expectation_quan附近，整个编码得到了优化。

2.3 m ing置乱算法的提出

而在实际的编码中，由于存在最后阶段没有足够的原始分组可供选择，所以设定阈值，当0.95K都被抛弃时，此时已编码M个编码分组，最后N-M个编码分组采用原来的编码算法。前M个和后来的N-M个采用的是两种编码算法，显然前者的效果更好，需要对编码分组和编码矩阵进行置乱，使得能够更好地体现在删除和高斯信道的性能，本文对于1×N维矩阵和N×N维矩阵提出ming置乱算法，其步骤如下：

1）选取Logistic方程作为模型的混沌序列发生器：xn+1=μxn（1+xn），这样每一个随机数都在 0和 1之间。

2）选取N×N维单位阵I，将第一个随机数乘以N得到操作数x，然后对x做[x]运算，将[x]列与第N列进行交换。

3）将第二个随机数乘以 N-1，然后对操作数做[x]运算，将[x]列与第N-1列进行交换。

4）重复第2个步骤，直至剩下最后1列为止。

这样能够保证每一个编码分组都能等概随机地排列在最后传输分组的任意位置。

3 新算法的实现

3.1 确定度分布

将原始数据等分为K个数据分组 （最后一个分组可以补0后成等分），根据输入码长K和输出码长N，选择weaken分布作为原始分布，计算出ping模型的期望和quan模型的期望。

3.2 第一阶段编码

根据设计的度分布Ω，随机地选取编码数据分组的度d，对每一个编码分组，从K个输入数据包中，等概率地随机选取d个不同的原始数据分组，计算这d个原始分组的ping值和quan值。当有原始分组满足公式（8）时，该分组舍去，从剩下的原始分组中随机选取不满足公式（8）的分组，直至d个原始分组都被选取，将这d个原始分组模二加，生成一个编码数据分组。

重复上述过程，统计已经满足公式（8）的原始分组个数，当其已经达到0.95K时，此编码过程结束，记下已经编码的编码分组个数M。

3.3 第二阶段编码

将剩下的N-M个未编码分组按照原先的编码方式编码，选取度分布值d，根据d随机选取原始d个原始分组，将这d个原始分组模二加，生成一个编码数据分组。

当N-M个编码分组编完后，将所有N个编码分组ming置乱，选择Logistic方程作为混沌方程，设定初始值μ，得到随机数列，进而得到置乱矩阵，对编码分组进行置乱，得到最终的传输分组。

3.4 译 码

当收到传输分组，首先根据初始值通过Logistic方程得到随机数列，对传输分组反置乱。

这里译码采用BP算法，所不同的是删除信道采用硬判决的BP算法，而高斯信道采用的是log-BP的软判决算法。译码算法根据编码数据分组与输入数据分组的对应关系建立二部图。在硬判决译码的每一步，译码器都在编码集合中寻找度为1的分组，这些分组组成的集合称为输出可译集合，具体译码如图3所示。log-BP的软判决算法相对复杂，本文就不再赘述。

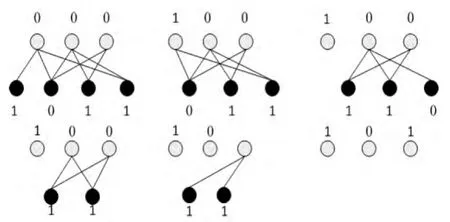
图3 BP硬判决译码图Fig.3 Diagram of BP hard decision decoding

在数据传输的过程中，会由于各种各样的原因发生数据分组的丢失和干扰，在常规的纠错编码中，当一个大的数据流发生超过其纠错能力的时候，会发生整个数据无法解码出来，但是喷泉码还会在一定程度上将一定数量的分组解码出来，本算法使得喷泉码在这两种信道性能进一步增强。

4 实验结果与讨论

本文分别进行LT编码和Raptor编码，原始分组长度K值取1 000，编码分组长度N值取2 000，为方便起见，每个分组只是0，1比特，置乱选择 Logistic方程，初始值 μ为 0.37，每个仿真节点仿真100次。

在 LT编码中，LT度分布采用 ideal、robust和 weaken分布，当有950个原始分组都已经达到要求被抛弃时，本文所采取的编码算法自动终止，采用原来的编码算法将剩下的编码分组全部编完，然后用ming算法将编码分组和编码矩阵进行置乱。

在Raptor码中，LT度分布采用weaken分布，首先进行LDPC预编码，将1 000个分组编码为1 050个分组，码率为0.95，然后将1 050个中间分组喷泉编码为2 000编码分组。

在LDPC预编码中，采用PEG的非规则编码，校验矩阵H的列的度分布函数为：

f（x）=0.283 54x+0.242 37x2+0.474 09x3（9）

当有1 000个中间分组满足条件被抛弃时，本文算法终止，采用原来的编码算法将剩下的编码分组全部编完，最后用ming算法将编码分组和编码矩阵置乱得到传输分组。

图4 ping模型分布图Fig.4 Distribution diagram ofmodel ping

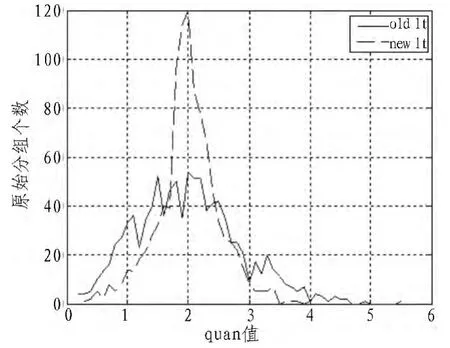
图5 quan模型分布图Fig.5 Distribution diagram ofmodel quan

如图4所示，在ping模型中，通过阈值设定，通过对比，原始分组明显向期望值11.7靠近，每一个原始分组对于编译码的贡献趋于一致。当0.95个原始分组被使用完，表明没有足够的原始分组可供利用，在ping值两端，会出现原有算法得到的ping，由于最后的编码数很少，对编译码没有太大的影响。

如图5所示，在quan模型中，通过阈值设定，原始分组向期望值2靠近，说明每一个原始分组的贡献也是一致的，这样能够避免在译码过程中由于信道的影响带来纠错性能的下降。

本文通过BEC信道和AWGN信道进行测试，其中BEC信道采用0.025的比例步长，删除概率从0.3到0.5进行测试，AWGN信道采用1db的信噪比步长，信噪比从-5db到0db进行测试，文献[9]的结果作为BEC信道的对比，而文献[10]的结果作为AWGN信道的对比。

图6 BEC信道误码率显示图Fig.6 Chart of BER in the BEC channel

图7 AWGN信道误码率显示图Fig.7 Chart of BER in the AWGN channel

测试结果如图6和图7所示，在高的删除概率下，本文采用的算法误码率明显降低，而且在零误码率的情况下所需的分组数也小于常规的方法。在低信噪比下，本文采用的算法比LT和Raptor常规的方法在相同的信噪比下误码率低，而且达到的误码率所需的信噪比也低于原来的方法。

5 结 论

本文通过对喷泉码原始分组的构成分析，提出ping模型和quan模型，使原始分组对于编码的贡献趋于一致，对中短码长的随机特性予以约束，避免原始分组被欠利用和过利用，这样提高了编码的效率，进而加强了抵抗干扰的能力，使得在干扰较强的情况下仍然有较低的误码率。由于阈值已经设定好，所以实现起来较为简单，保证绝大多数的原始分组的ping值和quan值都在期望附近，最后又提出ming置乱算法，使得每一个编码分组所携带的信息更为均衡。这样在降低复杂度的同时，又进一步提高了喷泉码的纠错能力。

[1]Luby M.LT codes[C]//Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science,2002,271-280.

[2]Shokrollahi A.Raptor codes[J].IEEE Transactions on Information，2006，52（6）:2551-2567.

[3]MacKay D J C.Fountain codes[J].IEE Proceedings on Communications，2005，152（6）:1062-1068.

[4]Palanki R，Yedidia Jonathan S.Rateless codes on noisy channels[C]//Proceedings of International Symposium on the Information Theory，2014:27-37.

[5]Singhal C，De S，Gupta H.M.User heterogeneity and priority adaptive multimedia broadcast over wireless[C]//Proceedings of 2014 IEEE International Conference on Communications，2014:1699-1704.

[6]Jing Yue，Zihuai Lin，Vucetic B，et al.Performance Analysis of Distributed Raptor Codes in Wireless Sensor Networks[J].IEEE Transactions on Communications，2013，61（10）:4357-4368.

[7]Sejdinovic D，Piechocki R J，Doufexi A，Ismail M.Fountain code design for datamulticastwith side information[J].IEEE Transactions on Wireless Communications，2009，8 （10）:5155-5165.

[8]Talari A，Rahnavard N.LT-AF codes:LT codes with Alternating Feedback [C]//Proceedings of 2013 IEEE International Symposium on Information Theory，2013:2646-2650.

[9]Zhu Zhiliang，Liu Sha，Zhang Jiawei，Zhao Yuli，Yu Hai.Performance Analysis of LT Codes with Different Degree Distribution [C]//Proceedings of 2012 Fifth International Workshop on Chaos-Fractals Theories and Applications（IWCFTA），2012:142-146.

[10]Haifeng Lu，Feng Lu，JianfeiCai，ChuanHengFoh.LT-W:Improving LT Decoding With WiedemannSolver[J].IEEE Transactionson Information Theory，2013，59（12）:7887-7897.