基于强跟踪UKF的室内目标跟踪

张英坤

（1.河北省科学院应用数学研究所，石家庄 050081；2.石家庄开发区冀科双实科技有限公司，石家庄 050081；3.河北省信息安全认证工程技术研究中心，石家庄 050081）

随着无线通信技术、微型计算机技术和传感器技术的快速发展，无线传感器网络[1-3]得到了广泛应用，目标跟踪[4-6]是其中一个重要的研究领域。在目标跟踪领域，基于卡尔曼滤波理论[7-10]的目标跟踪算法被应用于目标的状态估计。UKF滤波算法[11-13]是非线性系统中常用的滤波算法，其状态估计依赖于历史数据，当测量数据存在偏差时，容易导致滤波效果变差甚至发散。本文在分析标准UKF算法的基础上，利用强跟踪思想[14]对其进行改进，并搭建了基于无线传感器网络的测试平台，对强跟踪UKF算法的性能进行了验证。

1 实验环境的搭建

利用麻省理工大学的Cricket系统搭建一个基于无线传感器网络的可用于室内目标跟踪的实验环境，如图1所示。该网络由4个Cricket节点构成，被跟踪目标由机器人携带一个Cricket节点组成。Crieket节点利用射频信号和超声波脉冲之间的到达时间差来计算节点之间的距离。

图1 无线传感器网络Fig.1 Wireless sensor network

4个Cricket节点分布在已知的固定位置，同时发送射频信号和超声波脉冲，携带Cricket节点的机器人接收射频信号，当接收到射频信号后，启动超声波检测器等待接收相应的超声信号，检测到超声波脉冲时，利用射频信号到达时间和超声波脉冲到达时间之差来计算机器人与Cricket节点之间的距离。

2 系统模型的建立

本文研究的室内目标跟踪属于二维平面上的单目标跟踪问题，其跟踪过程可以描述如下：携带一个Cricket节点的机器人在4个Cricket节点构成的无线传感器网络中运动，根据机器人的运动方式建立机器人的系统模型，即状态方程和观测方程，再利用UKF算法迭代估计机器人的运动状态，从而实现对机器人的跟踪。下面给出机器人运动的状态方程和观测方程。

2.1 机器人运动的状态方程

采用如下状态方程来描述机器人的运动：

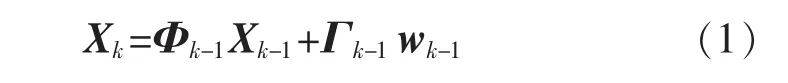
式中：Xk为机器人运动的状态向量，（xk，yk）为 k 时刻机器人的位置坐标；为 k 时刻机器人在X、Y方向的速度；Φk-1为状态转移矩阵；Γk-1为过程噪声输入矩阵；wk-1为过程噪声。

2.2 机器人运动的观测方程

假设无线传感器网络中的节点具有相同的噪声统计特性。当机器人在无线传感器网络中运动时，每个时刻均有4个节点检测到信号。令表示 k时刻第i个节点测量到的自身与机器人之间的距离，将其作为观测量，则有：

式中：（xi，yi）为第 i个节点的位置坐标。

3 基于强跟踪的UKF算法

3.1 UKF滤波理论

3.1.1 无迹变换

UKF算法的关键步骤是无迹变换UT（unscented transform），UT变换是一种计算非线性变换中随机变量数字特征的方法，其实现原理为在原先状态分布中按某一规则取一些点，使这些点的均值和协方差等于原状态分布的均值和协方差；将这些点带入函数中，相应得到非线性函数值点集，通过这些点集求取变换后的均值和协方差，其Sigma点的选择是基于先验均值和先验协方差矩阵的平方根的相关列实现的。具体计算方法如下：

（1）计算 2n+1个 Sigma点

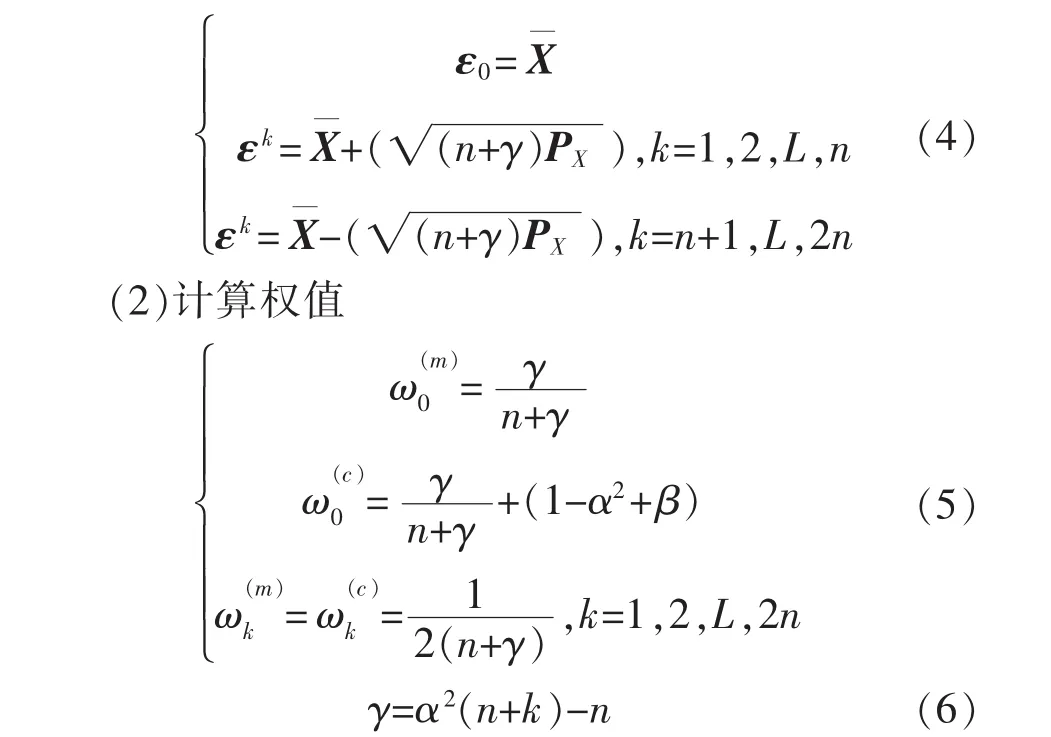
式中：n表示第n次采样；α常取为一个小的正值，如0.001，它决定了采样点相对于均值的分布情况；β为关于状态变量分布的先验知识在高斯分布时最佳取值为 2；γ为尺度调节因子；k通常取 0为均值的权值；为协方差的权值。

3.1.2 UKF滤波原理

考虑如下非线性模型：

其中：Xk为状态向量； f（·）为 n 维向量函数；hi（g）为m维向量函数；wk为过程噪声项，为高斯白噪声，服从 N（0，Qk）分布；Zk为观测向量；vk为量测噪声项，亦为高斯白噪声，服从 N（0，Rk）分布。

则UKF滤波计算过程如下：

步骤1初始化k=1，计算状态及协方差矩阵：

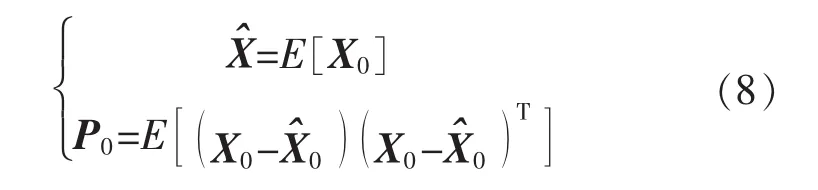
步骤2确定采样点：

步骤3时间更新：

步骤4观测更新：

步骤5滤波更新：

步骤6k=k+1，转至步骤2重复计算。

3.2 强跟踪滤波器对UKF的改进

强跟踪的充分条件是选择一个适合的时变增益矩阵Kk使得：

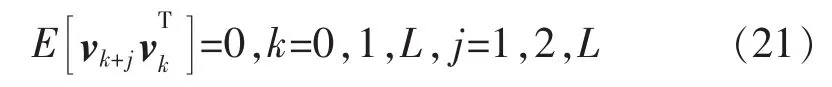
由于模型不确定性的影响，当滤波器的状态估计值偏离系统状态时，必然会在输出新息序列的均值和幅值上表现出来。若在线调整增益阵Kk，强迫式（21）仍然成立，使得新息序列仍然保持正交，则可以强迫强跟踪滤波器保持对实际系统状态的跟踪。强跟踪滤波器对UKF的改进主要表现在通过实时调整状态预报误差的协方差矩阵和相应的增益矩阵来达到。因此修改式为

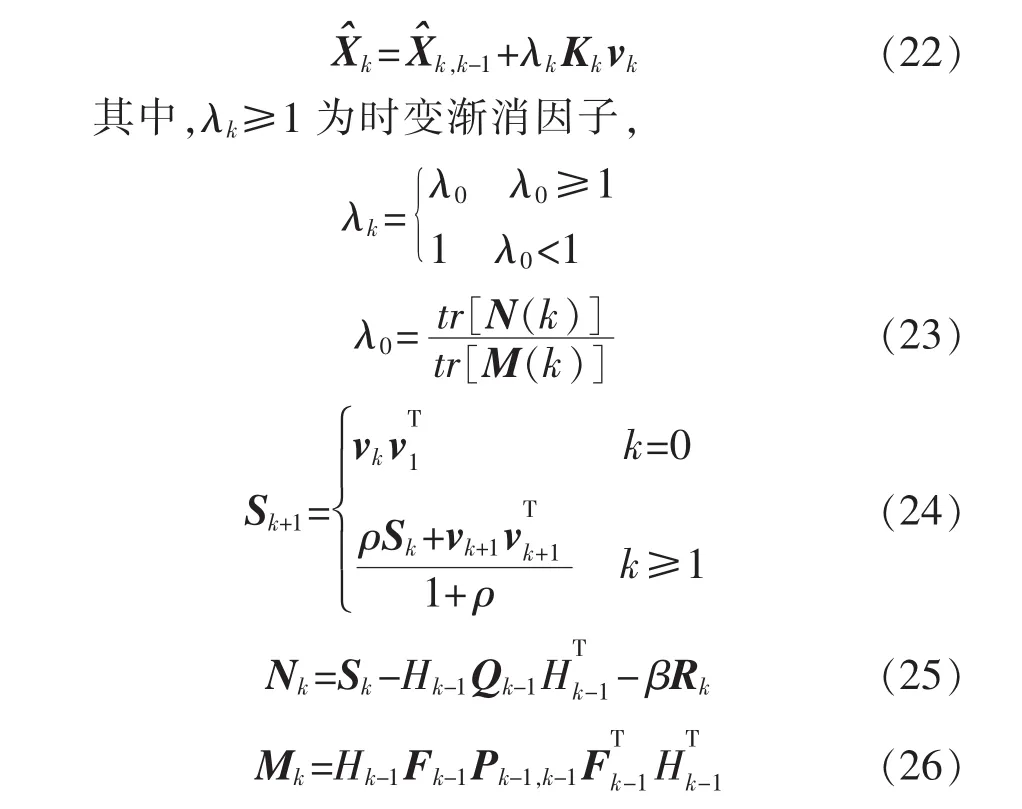
式中：0≤ρ＜1为遗忘因子，一般取 ρ=0.95；β≥1为一个选定的弱化因子，引入弱化因子的目的是为了使状态估计值更加平滑，此数值可以根据经验来设定，也可以通过计算机仿真来确定。

4 实验及结果分析

为了验证强跟踪UKF算法的性能，将其应用于本文搭建的无线传感器网络中。机器人携带的节点每隔0.5 s发射一次射频信号和超声波脉冲，其他4个节点则检测相应的射频信号和超声波脉冲，因此，采样周期T=1 s。机器人沿着中心位于（100 cm，100 cm）、半径为 50 cm的圆做匀速圆周运动，起始位置位于（150 cm，100 cm），角速度为则初始线速度近似为 （0 cm/s，8.73 cm/s）， 机器人的初始状态为 X0=（150 cm，0 cm/s，100 cm，8.73 cm/s）。

在上述条件下，采用强跟踪UKF算法与标准UKF算法的跟踪结果如图2、图3和图4所示。从图2可以看出，强跟踪UKF的跟踪曲线相较于标准UKF更加接近于预定轨迹；图3和图4分别给出了X方向和Y方向的跟踪误差绝对值曲线。从中可以看出强跟踪UKF的跟踪精度要明显优于标准UKF，且具有较好的鲁棒性。

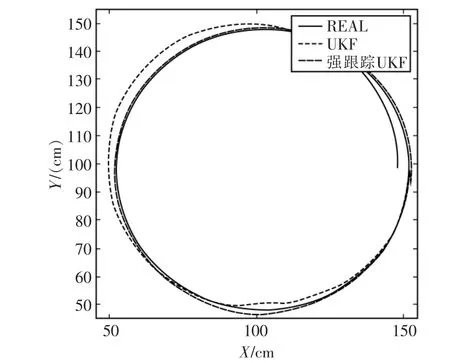
图2 跟踪轨迹曲线Fig.2 Tracking trajectory curve

图3 X方向误差绝对值曲线Fig.3 Error absolute value curve of X direction

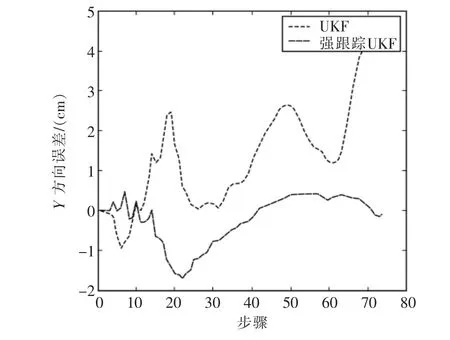
图4 Y方向误差绝对值曲线Fig.4 Error absolute value curve of Y direction

5 结语

为减少陈旧数据对目标跟踪过程产生的不利影响，本文对标准UKF算法进行改进，利用强跟踪思想修正协方差矩阵和相应的增益矩阵，搭建基于无线传感器网络的测试平台对强跟踪UKF算法的性能进行验证，实验结果表明，强跟踪UKF算法具有更高的跟踪精度，且鲁棒性较好。

[1]张健，李鸥.改进的无线传感器网络TDOA定位算法[J].计算机工程与应用，2010，46（16）：117-120.

[2]马灵芝.基于TDOA无线传感定位算法的研究及应用[D].山东：山东大学，2012.

[3]孙大洋，钱志鸿，韩梦飞，等.无线传感网络中多边定位的聚类分析改进算法[J].电子学报，2014，42（8）：1601-1607.

[4]权太范.目标跟踪新理论与技术[M].北京：国防工业出版社，2009.

[5]薛皓.时间异步条件下的无线传感器网络目标跟踪关键技术研究[D].北京：北京邮电大学，2009.

[6]侯杰虎.基于Kalman滤波器的视频运动目标跟踪算法研究[D].成都：成都理工大学，2012.

[7]付梦印，邓志红，张继伟.Kalman滤波理论及其在导航系统中的应用[M].北京：科学出版社，2003.

[8]秦勤.雷达目标跟踪的卡尔曼滤波方法的研究[D].大连：大连海事大学，2006.

[9]申逸.Kalman滤波技术在目标跟踪中的应用研究[D].湖南：国防科学技术大学，2006.

[10]王思思，齐国清.自适应SCKF在机动目标跟踪中的应用[J].电光与控制，2013，20（8）：6-10

[11]S Sarkka.On unscented Kalman filtering for state estimation of continuous-time nonlinear systems[J].IEEE Trans on Automation Control，2007，52（9）：1631-1641.

[12]刘慧霞，杨峰，梁彦.基于UKF的超视距雷达跟踪算法研究[J].计算机测量与控制，2005，13（10）：1094-1096.

[13]任福君，张秀华，姜永成，等.改进UKF算法在移动机器人定位系统中的应用[J].哈尔滨工程大学学报，2012，33（10）：1289-1294.

[14]陈巴特尔，周东华.强跟踪滤波器在倒立摆中的应用[J].控制工程，2012，19（1）：141-144.