基于邻域保持嵌入算法的间歇过程故障检测
梁秀霞,郑向博,郑晓慧
(河北工业大学 控制科学与工程学院,天津 300130)
间歇生产是精细化工,生物制药和食品饮料生产行业中主要的生产方式,随着市场需求的增长,间歇过程正朝着大规模、高复杂度的方向发展,一旦系统发生故障将危及人们的生命财产安全[1]。间歇过程数据维数多,耦合性强,利用原始数据难以建立准确的监控模型。传统的过程监控方法,如主成分分析(PCA)技术,都是利用数据的全局结构信息进行降维,在线监测阶段还需要对未来数据进行预估,降低了模型精度,忽略了数据之间的局部行为特征,埋没了系统的动态特性[2-4]。
针对以上的缺点和不足,本文提出了一种即时学习的局部正交保持嵌入学习算法。即时学习算法是一种自适应学习算法,旨在寻找与测试样本相似度最高的建模样本,从根本上提高监控模型的实时性;邻域正交保持嵌入算法旨在保持局部数据结构不变的同时实现数据降维,使得低维空间数据能够最大化地保留原始数据的可靠信息。文中将即时学习算法与邻域正交保持嵌入算法进行结合,兼顾了系统的局部特性和动态特性,使得统计量更加敏感地捕捉过程的变化,取得更好的监控效果。
1 基于正交约束的邻域保持嵌入算法(ONPE)
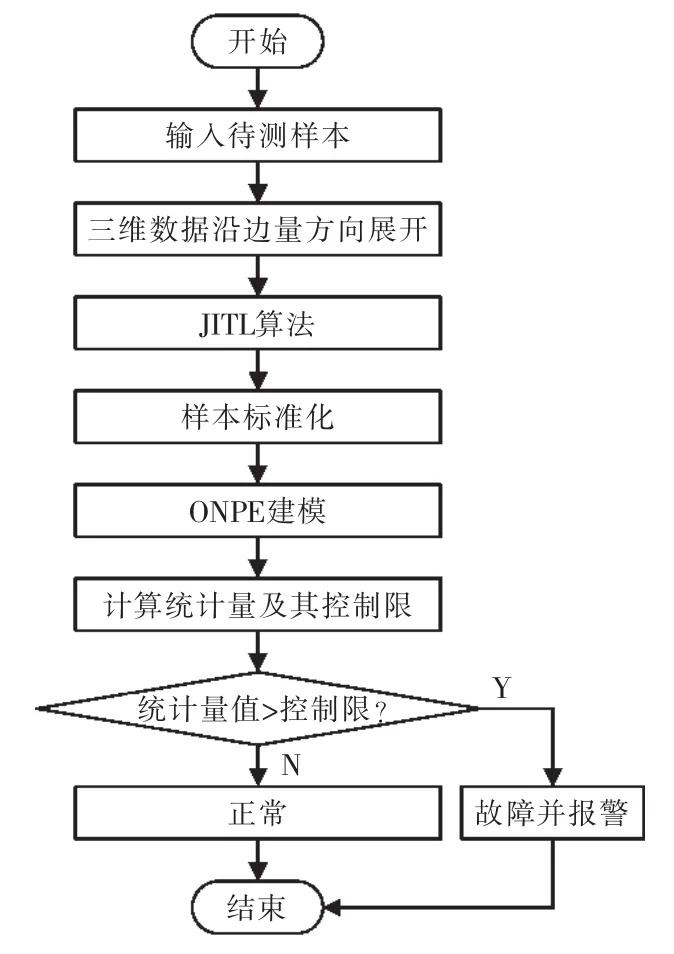
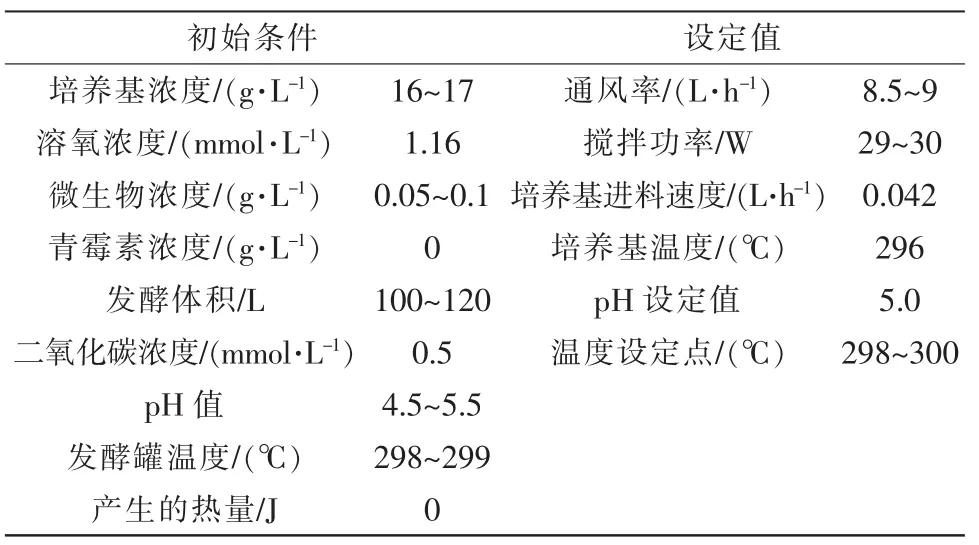
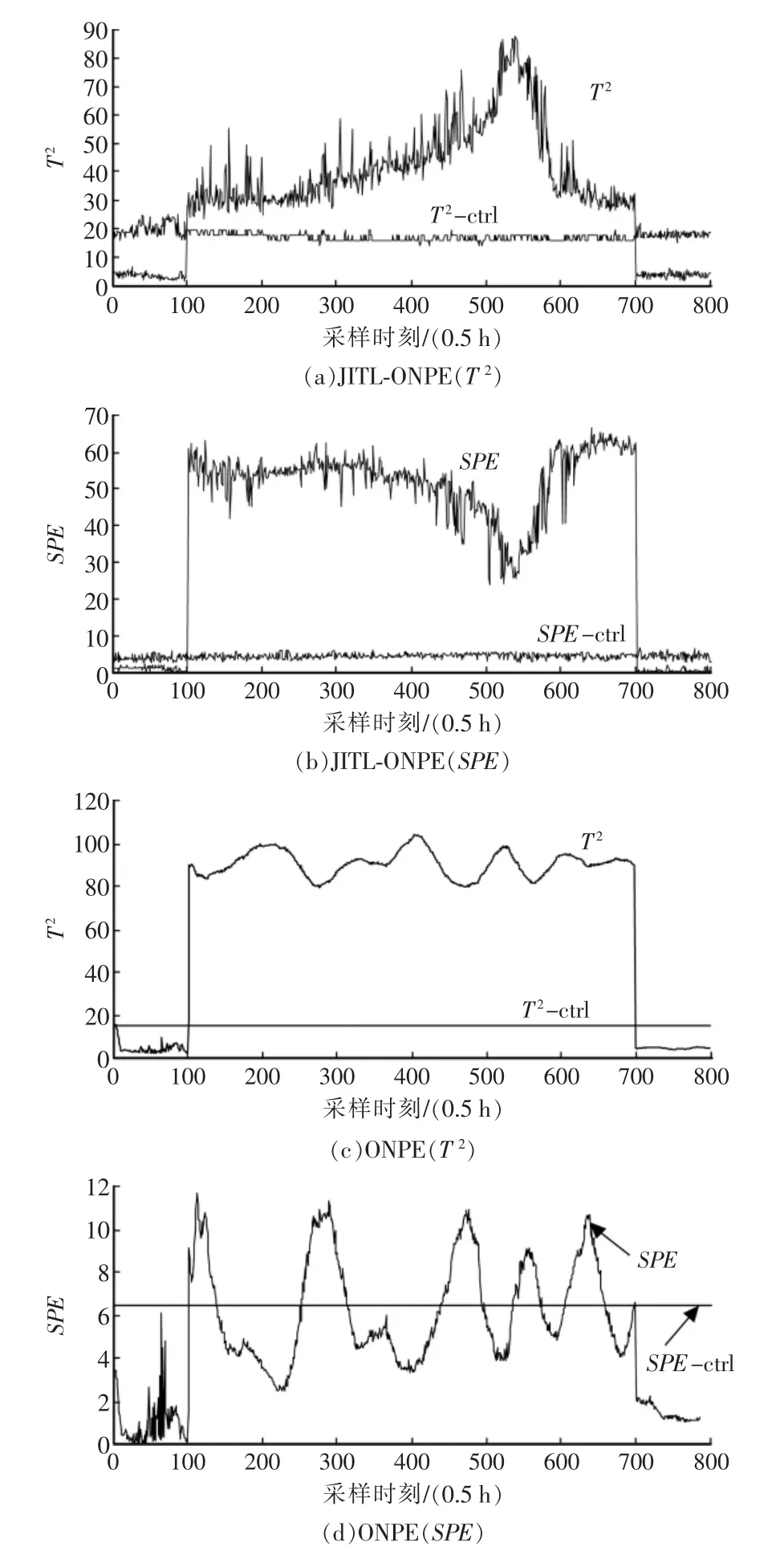
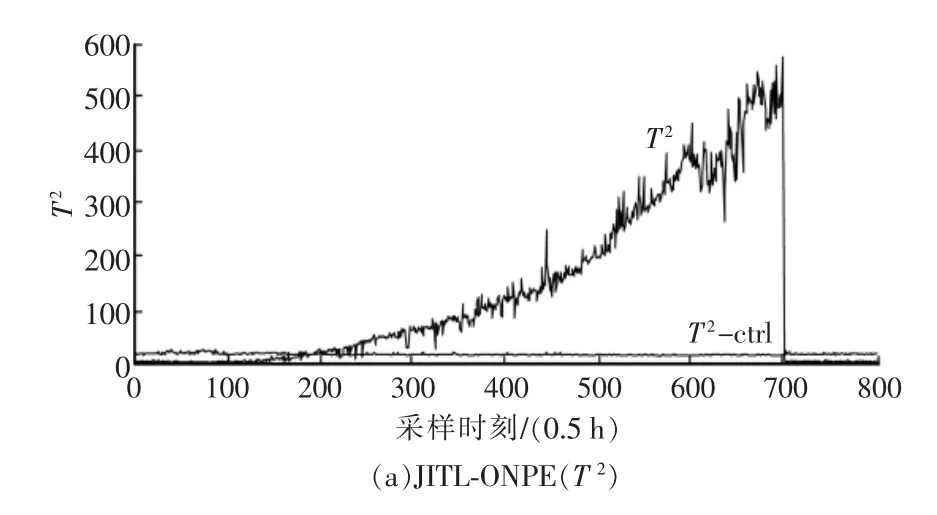
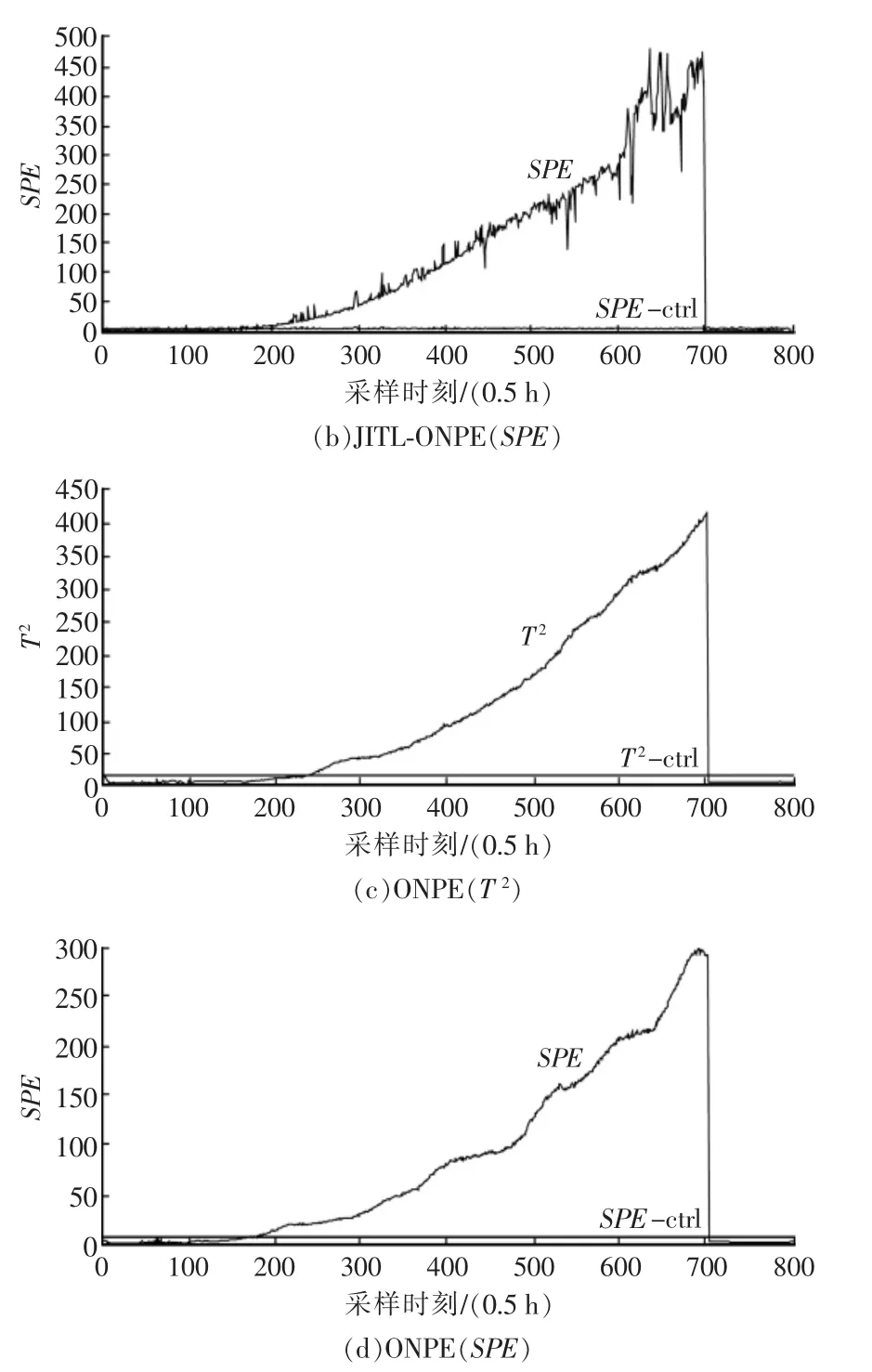
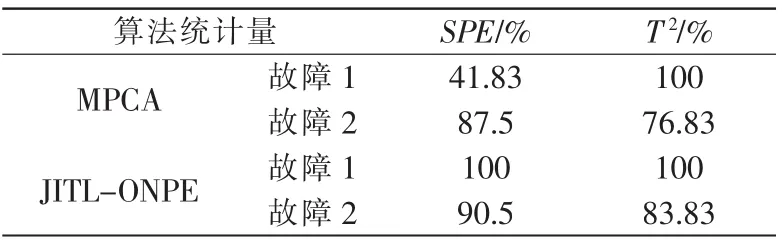
局部正交保持嵌入(ONPE)算法以非线性数据局部线性为基础,通过投影矩阵A,把原始数据空间X(x1,x2,…,xn)∈RD映射到低维空间 Y(y1,y2,…,yn)∈Rd(d 第1构建邻接图 计算每个样本点xi(i=1,…n)与其它样本点的欧氏距离 d,确定样本点 xi由近到远的 k 近邻(xj)kj=1。 第2确定权重矩阵 利用k个近邻点线性重构每个样本点,重构矩阵w通过最小化重构误差求得: 式中,wij是近邻xj对样本xi的重构系数,当xj不是xi的 k 近邻时,wij=0。 第3投影矩阵 NPE算法要求在低维空间Y中,空间中的任一元素能以相同的权重矩阵重构,即低维空间Y具有与高维空间相似的空间结构,投影矩阵通过最小化重构误差公式求得: 式中,M=(I-W)T(I-W)。 为提高系统的局部保持能力,非线性数据处理能力和特征提取能力,在式(1)的基础上加入正交约束条件为 式中,k=2,…d,利用拉格朗日乘子法包含约束求优得: 1)a1是(XXT)-1XMXT的最小特征值对应的特征向量; 2)ak是 Q(k)的最小特征值对应的特征向量。 式中:S(k-1)=[a(k-1)]T(XXT)-1a(k-1);a(k-1)=[a1,a2,…ak-1] 基于正交投影矩阵A,投影后的数据Y可以表示为 首先对正常工况下的数据进行建模,将原始数据空间分为特征空间Xˆ和X˜残差空间。ONPE算法通过监控统计量T2和SPE的波动进行故障检测[1,4]。依据主元分析算法计算方式,可得: 式中:A=B(BTB)-1为投影矩阵;E为残差矩阵。对于测试样本xnew可以写成如下形式为 根据主元分析法的统计量构造方式,与xnew相关的统计量分别为 式中:Λ-1=(YTY/(n-1))-1;T2和 SPE 统计量分别描述主元空间和残差空间的变化。相应的控制限为 式中:F(d,n-d;α)是自由度为 d 和 n-d,显著性水平为α的F分布。 其中,g和h是χ2分布的参数,满足条件:g=v/2m,h=2m2/v,m和v分别代表基于训练样本估计的SPE统计量的均值和方差。 针对间歇过程数据多维不等长特点以及过程的动态时变和多阶段特性,首先通过JITL算法找出在线建模数据;其次用ONPE算法对建模数据进行特征提取,求取投影矩阵,使投影空间与建模数据空间有相同的局部邻域结构;最后通过T2和SPE统计量对过程进行故障检测。 ONPE算法以非线性数据的局部线性特性为基础,通过处理数据的局部关系提取数据的主要特征,与NPE算法相比,有更好的局部结构保持能力和特征区分能力,与PCA算法相比能更多地提取数据的本质信息。然而间歇过程数据具有时变和多阶段特性,ONPE算法不能及时跟随系统的变化,即时学习(JITL)是一种基于数据驱动的在线建模策略,它的本质是自适应,能够准确地对非线性系统进行建模。因此将JITL策略与ONPE算法相结合建立的模型会更准确。在间歇过程中,JITL算法应用如下: 首先将三维的间歇过程数据X(I×J×K)沿变量方向展开为X(IK×J),其中I代表批次,J代表变量,K代表采样时间;间歇过程数据众多,有些训练样本与当前时刻样本差距很大,对数据进行全局搜索会浪费大量时间,影响自适应特性[6-8]。间歇过程多时段特性认为在采样时刻K附近的数据具有相似的性质,所以文章选择(k-Δk)…(k+Δk)时刻的样本为建模数据范围: 计算测试样本与S中每个样本的欧式距离di,将di从小到大排列,根据K近邻原则选取前K个样本作为建模样本 X。K 的大小以(dk-d1)/dk>0.1为标准,当大于0.1认为选取了足够的样本。 当检测到K时刻的测试样本xnew时,用ONPE算法求出正交投影矩阵A,即Y=ATX; 对于待测试的样本xnew,利用投影矩阵A得到降维数据ynew,即ynew=ATxnew,从而保证系统的实时性。 最后通过式(10)和(11)计算 T2和 SPE统计量,通过式(12)和(13)计算相应的控制限,比较统计量与控制限,判断是否故障。 JITL-ONPE监控方法可以简单描述为首先在线采样K时刻的数据作为待测样本,利用JITL方法从历史数据集中选取与待测样本最相关的样本数据,然后用挑选出来的样本集建立局部ONPE模型,最后用建立的模型对待测样本进行分析。综上所述,即时学习的局部正交保持嵌入算法具体步骤如图1所示。 图1 JITL-ONPE算法流程图Fig.1 JITL-ONPE algorithm flow chart 为验证JITL-ONPE算法的有效性,文章以青霉素过程为例,将JITL-ONPE算法应用其中,与ONPE算法相比较。文中共采用60组数据,其中58组正常数据和2组故障数据,取青霉素生产周期为400h,每隔0.5 h采样一次,共800个采样时刻。数据均来源于青霉素生产过程仿真软件Pensim 2.0,青霉素过程监控变量如表1所示,为检测模型监控性能,文章设置了2种故障,并且用2种方法对故障进行仿真[9]。 表1 青霉素过程监控变量Tab.1 Penicillin process monitoring variables 故障1、搅拌功率以7%阶跃减小,故障时间50~350 h;故障2、搅拌功率以3%持续减小,故障时间50~350 h。故障1和故障2的监控效果分别如图2和图3所示,当统计量(SPE和T2)超过其控制限(SPE-ctrl和 T2-ctrl)时表示系统故障。 图2 故障1的监控效果Fig.2 Monitoring effect of fault 1 图3 故障2监控效果Fig.3 Monitoring effect of fault 2 比较图2和图3容易看出,相较于ONPE算法,JITL-ONPE算法就有更好的监控效果。对于故障1,JITL-ONPE算法的T2和SPE统计量均可以准确检测出故障,满足系统的实时性要求,并且没有出现漏报误报情况;虽然ONPE算法的T2统计量能够及时发现故障,SPE统计量会出现误报和漏报情况,是监控结果不准确;对于故障2,ONPE算法和JITLONPE算法均发现故障,但是JITL-ONPE算法的T2和SPE统计量都比ONPE算法更早的发现故障,提高了系统的实时性,减少了系统的漏报率。表2中的数据也证明了这一点。 表2 算法准确率Tab.2 Algorithm accuracy 本文从数据的空间几何结构出发,将局部正交保持嵌入算法与即时学习算法相结合并成功应用于间歇过程,取得了良好的监控效果。JITL-ONPE算法不但弥补了全局特征提取算法的不足,而且满足了系统的实时性要求,但是算法仍然存在缺陷和不足,如基于数据符合单一分布,控制限的计算需要数据满足高斯分布等。今后应该仔细研究流行学习算法的优势与不足,结合实际应用,不断对算法进行改进提高,以取得更好的监控效果。 [1]杨洁.基于PCA的间歇过程监测及故障诊断方法研究[D].沈阳:东北大学,2010. [2]李波.基于流行学习的特征提取方法及应用研究[D].合肥:中国科学技术大学,2008. [3] 郭鹤楠.基于NPE和LDCRF的人体运动识别[M].长春:吉林大学,2011. [4]苗爱敏.数据局部时空结构特征提取与故障检测方法[M].杭州:浙江大学,2014. [5]Wang Guang,Yin Shen,Okyay Kaynak.An LWPR-based datadriven fault detection approach for nonlinear process monitor[J].IEEE,2014,10(4):2016-2018. [6]孙维,王伟.基于即时学习算法非线性系统多模型自适应控制[J].大连理工大学学报,2002(5):611-615. [7]毛振华.基于主元分析的自适应过程监控方法研究[M].杭州:浙江大学,2008. [8]Bontempi G,Birattari M,Bersini H.Lazy learning for local modelling and control design[J].International Journal of Control,1999,72(7-8):643-658. [9]曹岩,李明雨,李勇,等.MATLAB R2008数学和控制实例教程[M].北京:化学工业出版社,2009.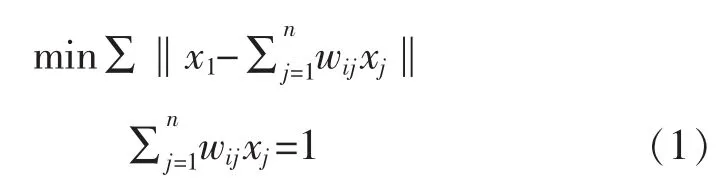
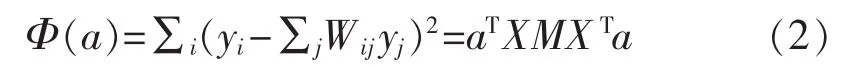
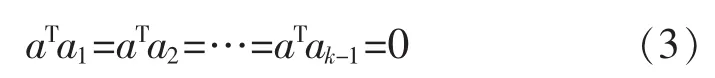
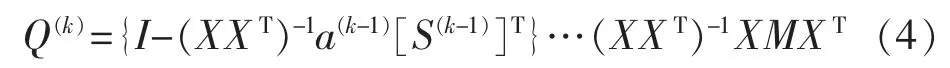

2 监控指标
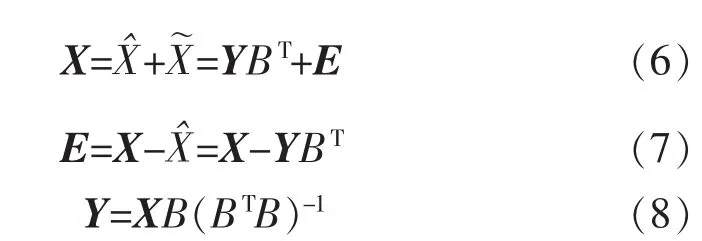
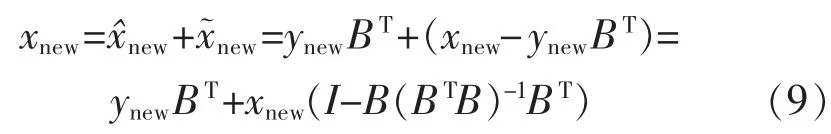

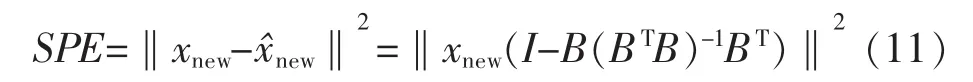
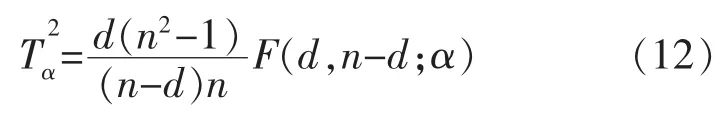

3 基于JITL-ONPE算法的故障检测
3.1 JITL-ONPE算法
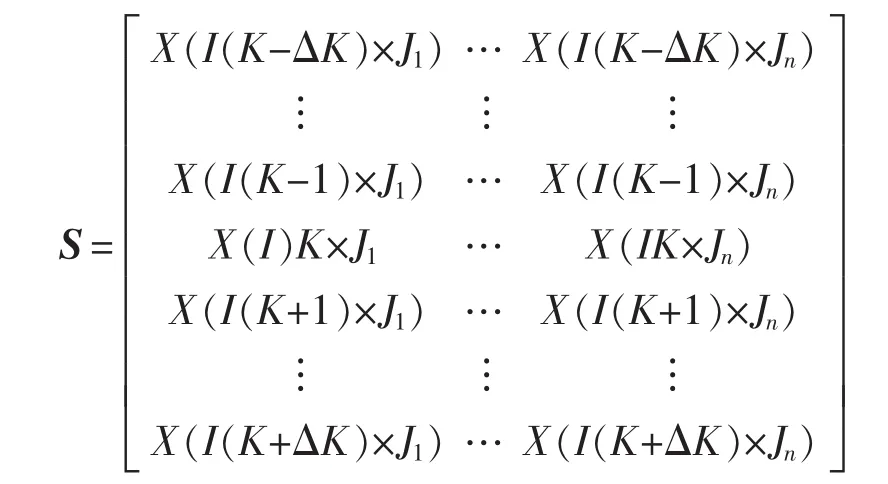
3.2 JITL-ONPE算法流程图
4 仿真分析
5 结语

