基于MEMS的捷联姿态系统的设计与试验

胡佳兴，魏延辉，刘 鑫，李光春

（哈尔滨工程大学 自动化学院，哈尔滨 150001）

捷联姿态系统采用惯性敏感器件MEMS三轴加速度计，三轴陀螺仪和三轴地磁传感器进行组合，构成微惯性测量单元MIMU，其应用效果与微机电MEMS传感器的性能息息相关[1]。相比于传统的捷联姿态系统，基于MEMS传感器的捷联姿态系统具有成本低廉、体积微型化、低功耗、质量可靠和优秀的抗冲击能力等特性[2]。

目前MEMS捷联姿态系统已经成为近年来国内外的研究热点之一，文献[3]中结合异构数据融合算法，采用互补滤波器实现了基于MEMS惯性器件的行人测量单元；文献[4]中应用MEMS惯性传感器，采用卡尔曼滤波器获得了人体部分的准确姿态估计；文献[5]中基于互补滤波器设计的MEMS/GPS/地磁组合导航系统，具有较高的姿态、速度和位置精度；文献[6]中提出了一种新的闭环姿态补偿算法进行MEMS惯性器件和GPS的组合导航，相比于传统方案有效抑制了惯导系统的误差积累；文献[7]中采用改进的自适应扩展卡尔曼算法应用于多旋翼无人机的姿态解算，具有较为优秀的动态性能。因此，随着MEMS惯性器件技术的不断发展，基于MEMS的捷联姿态系统将会有更加广阔的应用前景。

本文以MEMS陀螺加速度计和MEMS电子罗盘传感器组建捷联姿态系统，并对其误差建模和标定方法进行研究。

1 MEMS捷联姿态系统的设计

1.1 系统总体设计

本系统采用基于ARM-CortexM4内核的MK10-DN512VLK10微控制器为核心，采用MEMS传感器MPU6050和HMC5883L作为惯性传感器，利用液晶作为人机交互界面，通过蓝牙实现与上位机的信息通讯，完成系统的姿态测量和数据通讯、采集的功能。系统结构如图1所示。

图1 系统结构简图Fig.1 System structure diagram

基于MEMS的捷联姿态系统由于传感器精度较低的缺点无法敏感到地球自转角速度和因地球自转而产生的哥氏加速度分量[3]。因此若利用该系统实现位置、速度的数据解算在短时间之内就会积累较大的误差，无法进行实际应用。因此该系统在没有GPS、WiFi等参考信息辅助定位的情况下，只能够实现较为精确的载体姿态以及航向角的计算。

由于MEMS陀螺仪存在漂移的问题，在进行姿态估计中，随着时间的推进积累误差会不断增大，从而导致捷联姿态系统的姿态发散。因此，为了使捷联姿态系统稳定可用，需要与其它姿态传感器（加速度计、电子罗盘）组合使用，形成组合导航系统，才能够使获取到的姿态信息稳定可靠。捷联姿态系统的结构流程图如图2所示。

图2 捷联姿态系统的结构流程图Fig.2 Flow chart of the strapdown attitude system

1.2 MEMS惯性传感器

采用将加速度计和陀螺仪集成到一个芯片的器件作为传感器。Invensense公司的MPU6050是全球第一个整合型六轴运动处理组件，如图3所示，由于其将加速度计和陀螺仪整合到了一个器件之中，所以有效地减少了器件安装时的误差。同时MPU6050能够实现加速度计和陀螺仪多个量程配置，能够满足捷联姿态系统的需求。

图3 MPU6050系统图Fig.3 MPU6050 system diagram

1.3 MEMS三轴电子罗盘

采用霍尼韦尔公司的HMC5883L三轴电子罗盘芯片，该传感器为I2C通讯协议，应用于低成本罗盘和磁场检测领域。其内部集成了HMC118X系列的高分辨率磁阻传感器，并具有高精度信号放大、自动消磁和偏差校准功能，能使罗盘精度控制在1°～2°。因此该芯片被广泛应用于移动电话、笔记本电脑、消费电子、汽车导航系统和个人导航系统。HMC5883L的原理图如图4所示。

图4 HMC5883系统图Fig.4 HMC5883 system diagram

2 系统传感器输出数据的标定方法

2.1 加速度计误差模型及标定方法

加速度计精度较低，其误差模型为

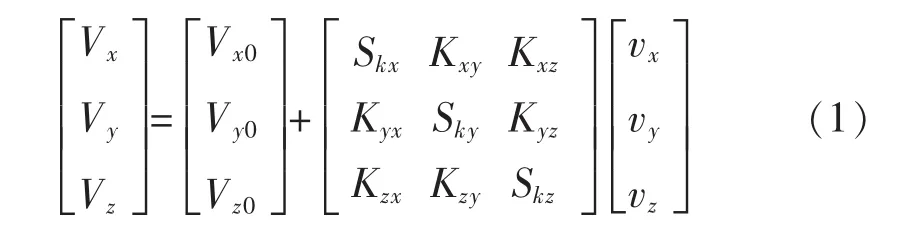
式中：载体坐标系下加速度矢量的投影分量为vx、vy、vz；加速度计多次采样的均值为 Vx、Vy、Vz；加速度计零偏为 Vx0、Vy0、Vz0；标度因数为 Skx、Sky、Skz；器件安装的误差系数为 Kxy、Kxz、Kyx、Kyz、Kzx、Kzy。

选用的MEMS加速度计为六轴MEMS传感器MPU6050中的三轴加速度计。量程配置为±8 g，标度因数为4096 LSB/g。因其精度较低，可以忽略因地球自转产生的哥氏加速度对加速度计敏感轴的分量[8]。

将捷联姿态系统固定于转台上，转动2次转台进行2次测量，得到加速度计X轴天向、地向的实际测量输出 VX+、VY+、VZ+与 VX-、VY-、VZ-。假设 α 为重力加速度在载体系的投影向量，g为当地的重力加速度，则α的表达形式在X轴天向时为［g 0 0］，X轴地向时为［-g 0 0］。

由加速度计的误差模型可以得到Y、Z轴加速度计测量值、零偏和系统安装误差之间的关系，即：

加速度计安装误差系数，可以由系统2次放置方式的平均值求差得到，即：

将式（1）展开，可得加速度计X轴均值与其它量的关系，即：

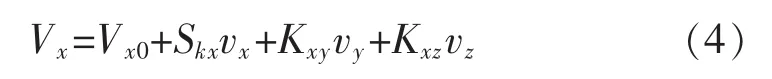
由式（4）可以得到X轴加速度计标度因数与零点偏置的求取方法，即：

若求取加速度计Y、Z轴的标度因数和零点偏置，只需要在转台上以 α＝［0 g 0］、α＝［0-g 0］、α＝［0 0 g］、α＝［0 0-g］4 个位置进行放置采集数据，通过计算即可获取。计算方法为

在系统进行转台实验时，首先调整系统的标定轴位置使其与转台轴平行，之后将其固定在转台的内框平台上，通过转台转动6个位置采集数据完成加速度计的标定。

2.2 陀螺仪误差模型及标定方法

采用的MEMS陀螺仪测量精度较低，因此不需要考虑交叉二次误差项对模型的影响[9]。陀螺仪的误差模型为

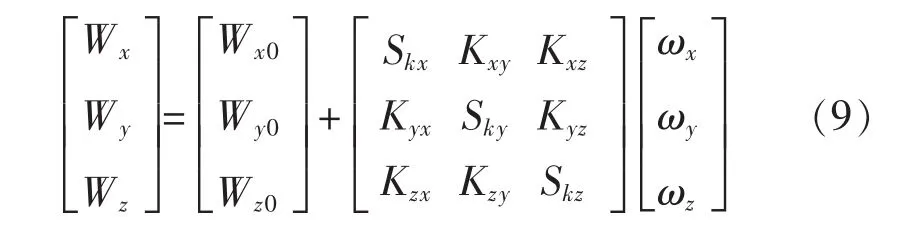
式中：陀螺仪多次采样的平均值为 Wx、Wy、Wz；陀螺仪零偏为 Wx0、Wy0、Wz0；标度因数为 Skx、Sky、Skz；安装误差系数为 Kxy、Kxz、Kyx、Kyz、kzx、kzy；载体坐标系下输入角速率的投影分量为 ωx、ωy、ωz。

MEMS陀螺仪为六轴MEMS传感器MPU6050中的三轴陀螺。其最大量程为±2000°/s，此时陀螺的标度因数约为 16.4 LSB·（°/s）-1。地球自转角速度约为 15.04°/h，即 0.00417°/s。通过参数的对照可以说明该MEMS陀螺的精度无法测量到地球自转产生的角速度，因此，在标定过程中，地球自转角速度对陀螺角速度输出的影响可以忽略不计。

将捷联姿态系统固定于转台上，令ω为载体坐标系相对于地理坐标系的角速率在载体坐标系的投影向量，令三轴转台分别以ω＝［ω10 0］、ω＝［-ω10 0］的参数进行旋转，转动2次转台进行2次测量，得到MEMS陀螺仪输出值Wx+、Wy+、Wz+与Wx-、Wy-、Wz-。

由陀螺仪的误差模型可以得到，Y、Z轴陀螺仪测量值、零偏和系统安装误差之间的关系，即：

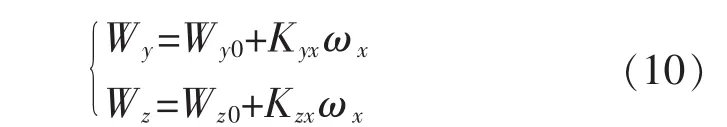
陀螺的安装误差系数，可以由系统2次放置方式的平均值求差得到，即：

将式（11）展开，可得加速度计X轴均值与其它量的关系，即：

由式（12）可以得到X轴陀螺标度因数与零点偏置的求取方法，即：

若求取陀螺仪Y、Z轴的标度因数和零点偏置，只需要在转台上以 ω＝［0 ωy0］、ω＝［0-ωy0］、ω＝［0 0 ωz］、ω＝［0 0-ωz］旋转采集数据，通过计算即可获取。计算方法为

在系统进行转台实验时，首先调整系统的标定轴位置使其与转台轴平行，之后将其固定在转台的内框平台上，在转台进行旋转实验时采集数据完成陀螺的标定。

2.3 电子罗盘误差模型及标定方法

若要对椭圆进行修正，首先应该将椭圆的一个中心与坐标系的原点重合，之后通过系统的标度因数对椭圆进行拟合使其恢复圆形从而完成补偿[10]。电子罗盘的误差模型公式为

式中：Hxoff和Hyoff为偏移量；Hxsf和Hysf为标度因数；用作计算航向角的 Hx和 Hy可表示为 Hx′、Hy′。

在捷联姿态系统的实际应用环境中恒定磁场的干扰强度一般是稳定不变的，因此可以在该环境下对电子罗盘的输出数据进行标定来提高航向角的精度。在实际标定中，首先将电子罗盘的数据进行采集，围绕水平面360°旋转一周，然后根据X轴和Y轴的磁场强度数据计算得到最大值和最小值Hxmax、Hxmin、Hymax、Hymin，通过这 4 个数值便可以求出对应的偏移量和标度因数。计算方法为

经过补偿后的电子罗盘数据如图5所示，此时电子罗盘输出的磁场数据已经修正为接近圆形的形状。

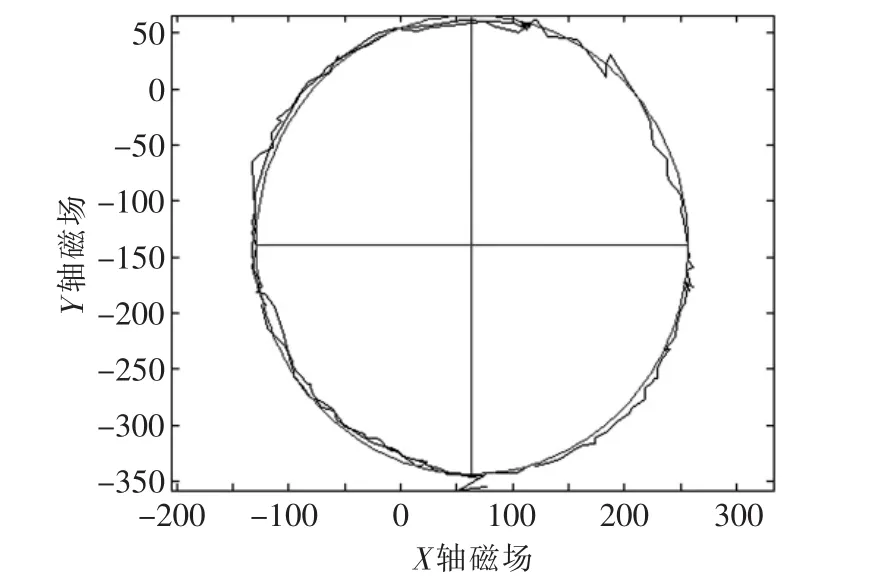
图5 经过椭圆修正后的电子罗盘数据图像Fig.5 Electronic compass data corrected by the changes in the elliptical image

由于环境的地磁矢量随着地理位置的不同会存在一定的变化，因此在更换载体的地理位置之后，需要对电子罗盘重新进行修正，以保证航向角的精确度。

3 系统性能试验

3.1 静态性能验证

系统的静态精度测试方面，首先将系统静止放置采集数据，然后对3个轴分别进行单次转动，采集数据发送至上位机，通过Matlab绘制出波形。如图6所示为捷联姿态系统在静态下经过卡尔曼滤波输出的欧拉角的波形图像。

图6 捷联姿态系统在静态下的波形图像Fig.6 Strapdown attitude system waveform images under the condition of static

在系统的静态测试中，用手对系统沿1个轴进行1个角度的转动，由于是用手旋转精度较低，因此在沿某1个轴旋转时另外2个轴也会有较小的角度变化。通过图6可以看出系统输出的姿态信息在系统旋转后迅速反应，并能够较快地收敛并趋于稳定，说明该系统具有较好的稳态性能。经过对实验数据的分析，系统在静态条件下横滚角浮动范围为±0.2°，俯仰角浮动范围为±0.2°，航向角浮动范围为±1°。

3.2 动态性能验证

在捷联姿态系统的动态性能验证上，对系统施加了较大的姿态变化，进行了单轴运动和多轴运动2种测试方式。由于是用手旋转捷联姿态系统存在一定的误差，因此当进行单轴旋转测试时其它轴的角度输出也会有较小的变化，实验图像如图7所示。

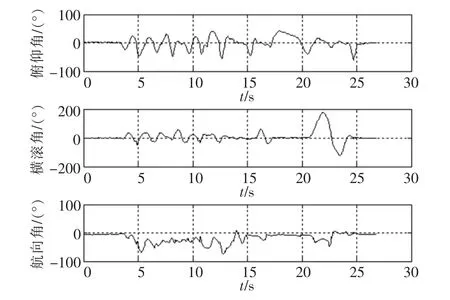
图7 捷联姿态系统在动态下的波形图像Fig.7 Strapdown attitude system waveform images under the condition of dynamic

通过图像可以得知，系统的欧拉角在载体运动后迅速收敛并且维持稳定，由于是用手旋转系统，因此由于运动精度的影响导致在绕1个轴运动时其它轴输出的角度也会有较小的角度变化。

4 结语

本文阐述了基于低成本的MEMS捷联姿态系统的发展现状，针对低成本高性能的要求，设计了具有互补功能的MEMS捷联姿态系统。通过对系统试验得到的数据进行分析，该系统在静态时能够较快地收敛并趋于稳定，在动态测试时能够快速地进行跟踪和收敛，证明了该系统具有较好的稳态性能和动态性能。

[1]唐大全，刘锦涛，张博.微型捷联姿态系统的硬件设计[J].自动化仪表，2007，28（1）：15-18.

[2]郭访社，于云峰，刘书盼，等.捷联惯性导航系统姿态算法研究[J].航天控制，2010，28（1）：37-39.

[3]Fourati H.Heterogeneous data fusion algorithm for pedestrian navigation viafoot-mounted inertialmeasurementunitand complementary filter[J].IEEE Transactions on Instrumentation and Measurement，2014，64（1）：221-229.

[4]Zihajehzadeh S，Loh D，Lee M，et al.A cascaded two-step Kalman filter for estimation of human body segment orientation using MEMS-IMU[C]//Engineering in Medicine and Biology Society（EMBC），2014 36th Annual International Conference of the IEEE，2014：6270-6273.

[5]张勇刚，张云浩，李宁.基于互补滤波器的MEMS/GPS/地磁组合导航系统[J].系统工程与电子技术，2014，36（11）：166-173.

[6]赵文杰，方舟，李平.基于地磁场矢量误差反馈的姿态补偿算法[J].浙江大学学报：工学版，2014，48（9）：169-174.

[7]张欣，白越，赵常均，等.多旋翼姿态解算中的改进自适应扩展Kalman 算法[J].光学精密工程，2014，22（12）：238-244.

[8]宋丽君，秦永元.MEMS加速度计的六位置测试法[J].测控技术，2009，28（7）：11-13.

[9]宋丽君，秦永元.MEMS陀螺仪的一种实用标定法[J].压电与声光，2010，32（3）：372-374.

[10]闻秋香，罗向前，孙君道.磁罗盘工程校准方法研究[J].科学技术与工程，2011，11（28）：158-161.