基于大数据的多尺度系统软测量方法及其应用

杨 彬

（中环天仪股份有限公司，天津 300384）

随着信息技术的进步，大数据的存储和使用成为可能，将基于大数据的分析方法用于软测量中，可以实现多种难以测量或者暂时不能测量的重要参数的检测。

论文在定义多尺度系统的基础上，提出一种基于大数据的软测量方法，并将之用于锅炉辐射受热面灰污程度的软测量。

目前辐射受热面灰污监测的方法主要有加装热流计，测量各点的热流量反映其灰污程度[1]；采用传热学理论计算以实现灰污监测[2]；采用数值模拟的方法计算炉膛内温度场的分布状况，获得受热面的灰污程度等[3]。然而当前的方案或存在投资成本高、维护困难的问题，或存在部分重要参数，如火焰中心位置、煤质等，在目前的技术水平下无法测量的问题[4-8]，因此上述监测方法难以获得令人满意的效果。

采用本文提出的算法，可以在一定程度上解决辐射受热面灰污程度的软测量问题，为进一步的吹灰优化等提供技术依据。

1 多尺度系统

对一个非线性时变系统：Y=f（U，t）将输入 U、输出Y做k尺度小波变换，um∈U，yn∈Y可分解为细节分量重构信号 um1、um2…umj，yn1、yn2…ynj， j=1，…，k，以及近似分量重构信号 uma、yna，定义：

um、yn的第j尺度细节分量重构信号能量pdet（umj）、 pdet（ynj）为

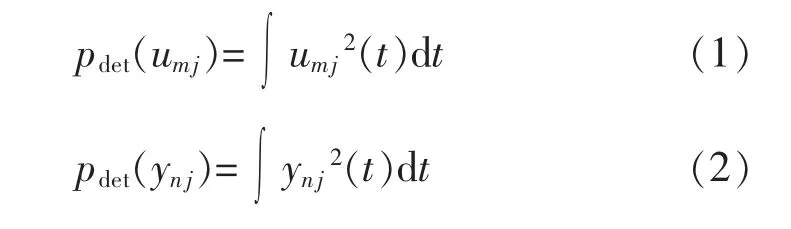
um、yn的第j尺度近似分量重构信号能量papp（uma）、papp（yna）为

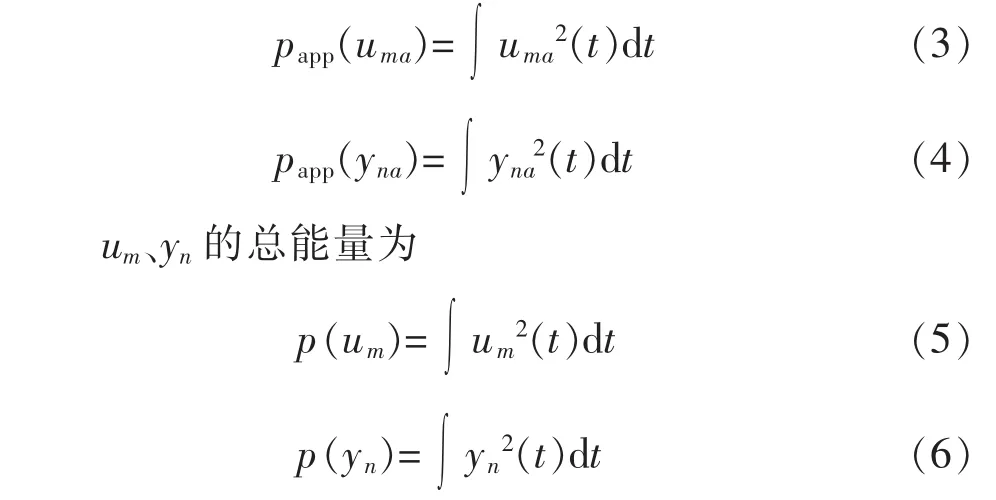
um、yn的细节分量重构信号能量与近似分量重构信号能量代表了系统变量分布在不同尺度下的能量，其大小表明参数在此尺度上分布的强弱。

基于上述信号能量，可以定义um、yn的多尺度相对能量矩阵A、B如下：

多尺度相对能量矩阵A、B分别表明了输入、输出变量分布在不同尺度下的分量间强弱关系，利用多尺度相对能量矩阵A、B，可以定义多尺度系统如下：

当0＜∑aij＜∞时，说明系统的输入在每一个尺度上都存在分量，此时称非线性时变系统Y=f（U，t）为输入多尺度系统；

当0＜∑bij＜∞时，说明系统的输出在每一个尺度上都存在分量，此时称非线性时变系统Y=f（U，t）为输出多尺度系统；

当条件1与条件2同时满足时，称非线性时变系统 Y=f（U，t）为输入输出多尺度系统。

非线性时变系统的输入往往无法通过测量全部获取，对形如 Y=f（V，W，t）的非线性时变系统，其中vi∈V为系统可测输入，wi∈W为系统不可测输入。 此时，由于无法按式（7）、（8）计算系统的多尺度相对能量矩阵A，因此无法判断是否属于多尺度系统。

考虑在工程实际中，通常采集到的信号是长度有限的，故在此前提下对系统进行分析时，可以认为是有限长度的变量，此时满足：

即wi可以进行快速傅里叶变换，分解为不同频率的分量，且对某一频率范围 Φ∈［fjl，fjh］，通常满足：

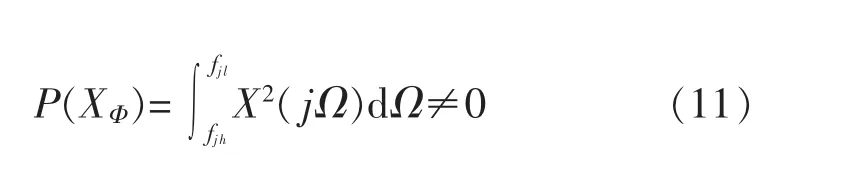
其中：fjl、fjh分别为对wi做k尺度小波变换后第j尺度上信号的频率范围。因此，对实际系统，不可测输入wi具有多尺度特性。

将上述结论推广至可测输入V及输出Y，可以看出对实际工程中出现的非线性时变系统，通常满足输入、输出的多尺度相对能量强度矩阵∑aij＜∞、∑bij＜∞，即可以看作输入输出多尺度系统。

2 基于大数据的多尺度系统软测量方法

论文提出的基于大数据的多尺度系统软测量方法核心在于利用工业信息系统中的大数据，建立软测量对象的基准模型，而后将设备运行中的可测信息与基准模型提供的参考信息进行比较构成残差序列，并通过对残差序列的多尺度分析构成系统的软测量参数。

在工业生产过程中，设备并不总是固定在某个工况点运行，操作人员会根据生产需要、调度指令等对设备的工作状态进行调整。在调整过程中，各个参数会发生不同程度的波动，即设备处于动态变化的过程中，这种工况是一种临时的、非稳态的。

由于基准模型不但依赖于数据的真实性，而且要求各数据间具有较强的一致性，即在确定运行边界的条件下，用于描述设备运行状态的众多变量符合确定的对应关系。由于工业过程通常具有大延迟、大滞后的特性，上述要求通常只有在设备长时间稳定运行时可以实现。因此，为了提高算法的精度，论文同时建立了系统的动态工况基准模型与稳态工况基准模型。

动态工况基准模型是指利用经过预处理的建模数据建立的、包含设备运行动态过程的模型。尽管动态过程中存在严重的不一致现象，但动态工况运行数据通常占有极大比例，将其舍弃意味着浪费了大量富含信息的数据。通过机理分析、统计分析等方法，可以改善动态工况的建模品质。

稳态工况基准模型是指利用提取了稳态工况的原始数据建立的、只包含设备稳态运行时参数对应关系的模型。

系统稳态工况的判定方法是，在时间区间［t1，t1+Δt］内，建模变量 xi满足：

其中：xi，max、xi，min分别为 xi在时间区间［t1，t1+Δt］内的最大值和最小值；xi，e为在此工况下的额定值；δk为波动阈值；Δt及δk应根据对象的实际特性确定。

动态工况基准模型与稳态工况基准模型反映了系统不同状态下参数间的对应关系。在建立基准模型的基础上，将运行数据代入动态工况基准模型中，可以获得系统动态过程的预测值为

对数据仓库中的运行数据按式（12）提取稳态工况，将稳态工况运行数据代入稳态工况基准模型中，可以获得系统稳态过程的预测值为

其中：yi，preDYM、yi，preSTD分别为动态模型预测值与稳态模型预测值；｛xi|xi∈［（x1，x2，…，xn）］｝为对象动态运行数据；｛xi′|xi′∈［x′1，x′2，…，x′m］｝为对象稳态运行数据。

将 yi，preDYM、yi，preSTD分别与实际运行数据比较，如式（15）、（16）所示，可以获得系统的动态残差 erri，DYM以及稳态残差 erri，STD为

其中：yi、yi′分别为实际运行数据及稳态运行数据。

由于大数据的海量性，将大数据的串行处理转变为并行处理，可以极大提高计算效率，降低计算时间。为此，论文基于信息粒化的思想，将上述动态残差及稳态残差进行有机结合，形成多个信息粒，而后通过对信息粒的并行计算降低状态监测算法运行时间，节约运算资源。

由于系统总是处于稳态→动态→稳态交替运行的过程中，因此可以基于系统这种动态、稳态的交替过程划分信息粒，即以系统的一个动态过程，或者数个连续动态过程及其相对应时间的稳态过程组成一个信息粒。

在信息粒内，稳态残差与动态残差属于异步信息，二者可以看作是2种不同的传感器对融合残差异步观测的结果。因此论文基于卡尔曼滤波，建立了一种简单高效的异步信息融合算法，利用稳态残差构建对象的差分方程，对动态残差进行滤波，以此获得二者的最优估计—融合残差。算法可以通过回归分析，利用信息粒中的稳态残差，建立融合残差的差分方程为

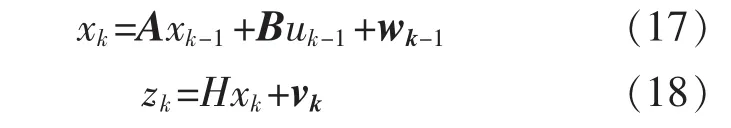
其中：wk和vk分别为过程激励噪声和观测噪声的协方差矩阵。

系统的稳态工况基准模型精确度高，且系统在稳态工况时噪声较动态工况小，因此可以认为过程激励噪声的协方差矩阵wk为一个较小的常数γ。

观测噪声通常处于高频段，其协方差可以由动态残差小波变换细节重构估算出来：

其中：W（s，err）为动态残差 errDYM在第 s尺度上小波变换的细节分量的重构。

在确定了卡尔曼滤波器的参数后，可以使用卡尔曼滤波算法，对动态残差进行滤波，获得二者的最优估计—融合残差。

3 锅炉辐射受热面灰污的软测量

论文研究数据来自某电厂1000 MW超超临界机组，锅炉为直流、单炉膛、一次再热、切圆燃烧方式。

基准模型需要反映辐射受热面无灰污染时，各变量的对应关系。工质吸热动态工况基准模型为

其中：Hslbout为水冷壁出口工质焓值，kJ/kg；Hslbin为水冷壁入口工质焓值，kJ/kg；F为锅炉给水流量，t/h；Bfuel为燃料量，t/h。

基准模型表明单位燃料量释放的热量引起的水冷壁工质焓升。相同工况下，水冷壁无灰污染时，受热面热阻较小，工质可以吸收较多的热量，而当灰渣逐渐在管壁外层积累，受热面热阻增加，接收相同辐射能时，工质只能吸收少部分能量，其焓升会大大降低。因此，利用工质在受到相同辐射传热时吸热量的多少可以反映出受热面灰污染程度的高低。

由于煤燃烧释放的热量不仅被辐射受热面吸收，还要供应给炉膛顶部的顶棚过热器，以及后续的二级、三级过热器、再热器等。因此不同受热面吸热量的分配会对式（20）的工质吸热量造成影响，如表1所示。

表1 受热面吸热量Tab.1 Heat requirement of heat-exchanger

从表1可以看出，对中、高负荷，水冷壁吸热量占系统总吸热量的50%左右，波动基本不超过1%，因此，可以认为在中、高负荷下，锅炉正常燃烧时水冷壁吸热量占系统总吸热量的比例基本维持不变。

论文选取了机组运行16 h的数据，此时机组运行于中、高负荷，如图1所示。基于式（12）提取系统稳态工况，利用式（20）建立的动态工况基准模型和稳态工况基准模型的预测值与实际运行值进行比较，构成动态残差与稳态残差，结果如图2所示。

图1 机组负荷Fig.1 Unit load

图2 稳态残差与动态残差Fig.2 Residuals of dynamic state and steady state

论文以每相邻2个稳态残差以及对应时间的动态残差组成一个信息粒，以其中一信息粒i为例，融合残差的差分方程为

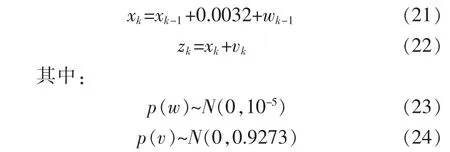
则此信息粒的稳态残差、动态残差、融合残差如图3所示。

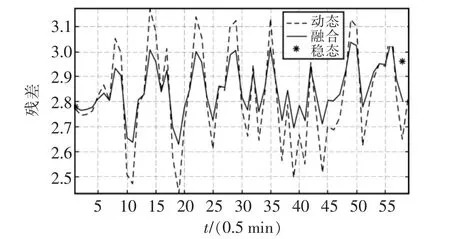
图3 信息粒残差Fig.3 Residuals of information granule

将全部信息粒进行处理，可以得到辐射受热面吸热量的融合残差，如图4所示。

从其统计数据可以看出，煤质在16 h的运行时间内不断变化，但平均变化率较低，其波动大部分表现为一种中、高频的小范围抖动。因此，煤质对状态监测结果的影响可以看做为一种中、高频干扰，其余未建模噪声与煤质波动具有类似的特性。通过基于小波变换的多尺度分析算法，采用haar小波基，提取其低频分量作为锅炉受热面污染度指数，用以反映其灰污程度，结果如图5所示。

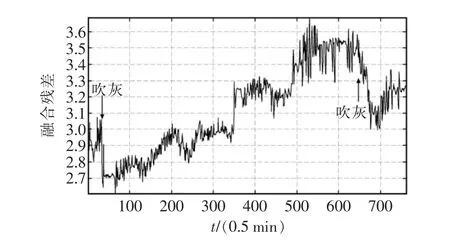
图4 融合残差Fig.4 Fusion residuals

图5 辐射受热面污染度指数Fig.5 Ash pollution index of radiant heating surface

4 结语

论文提出了一种基于大数据的多尺度系统软测量方法，利用工业信息系统中的大数据建立系统的基准模型，并将运行数据与基准模型的预测数据进行比较构成残差序列，进而通过对残差序列的多尺度分析构造研究对象的软测参数，实现系统的软测量。论文以某机组辐射受热面灰污染程度的软测量为例，验证了算法的有效性。

[1]杜庆军.电站锅炉吹灰优化系统的研究与应用[D].北京：华北电力大学，2009.

[2]蓝晓村.电站锅炉灰污监测与吹灰优化的应用研究[D].南京：东南大学，2005.

[3]张春丽.电站锅炉吹灰优化系统的研究与开发[D].北京：华北电力大学，2007.

[4]Piboontum S J，Swift S M，Conrad R S.Boiler modeling optimizes sootblowing[J].Power，2005，149（8）：34-37.

[5]Kalisz Sylwester，Pronobis Marek.Investigations on fouling rate in convective bundles of coal-fired boilers in relation to optimization of sootblower operation[J].Fuel，2005，84（7-8）：927-937.

[6]Erkki Valimaki，Keijo Salmenoja.Measured data for sootblowing optimization[C]//2004 TAPPI Fall Technical Conference：Engineering and Pulping，October 31，2004-November 3，2004，Atlanta，GA，United states，2004.

[7]Erkki Valimaki，Keijo Salmenoja.New tools for sootblowing optimization studies[C]//Asian Paper-New Applied Technology Conference，April27，2004-April29，2004，Suntec，Singapore，2004.

[8]Sarunac Nenad，Sale John W，Bian Xiadong，et al.Sootblowing optimization for opacity control[C]//EPA-DOE-EPRI-A and WMA PowerPlantAirPollutantControlMegaSymposium 2006，August 28，2006-August 31，2006，Baltimore，MD，United states，2006.