基于模糊PI控制的开关磁阻电机调速系统的MATLAB仿真
李 锋,刘 芬,王宝忠
(江苏科技大学 江苏 镇江 212000)
开关磁阻电机调速系统 (SRD)主要由开关磁阻电机(SRM)、功率变换器、控制器、位置检测和电流检测五个部分组成[1]。其中SRM具有开关性和磁阻性,结构简单、坚固、调速性能优越。但是由于开关磁阻电机定子齿、转子齿交叠前产生的边缘磁通引起电流的非线性变化。所以一般线性结构控制器难以满足SRM的非线性要求[2]。
传统的PI控制存在超调、调节精度低、系统震荡等一些问题。模糊控制则是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的计算机智能控制,在调速系统中对系统的非线性变化有很强的适应性[2]。本文将模糊控制和PI算法相结合,利用模糊推理对PI的参数进行实时的在线调整,控制四相8/6极开关磁阻电机的调速系统,有效地改善了SRM非线性问题,SRD的响应速度,调节精度和稳定性都大大提高,达到了较为理想的控制效果。
1 模糊控制器的原理和结构
1.1 模糊PI控制调速原理
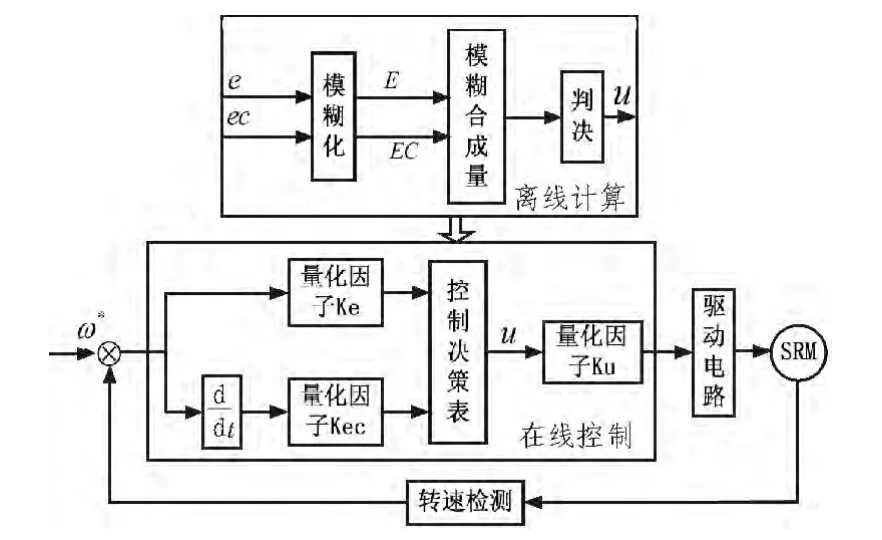
图1 基于模糊PI控制的SRD系统控制流程图Fig.1 SRD system control flowchart based on fuzzy PI control
如图1所示,转速检测模块根据转子的位置信号,计算出转子的转速,然后与给定的转速相比较,得到转速的偏差e和偏差变化率ec。将e和ec,通过模糊PI控制算法,再依据当前的速度实际值,进而调节各相PWM的占空比,从而实现速度闭环的控制。
1.2 模糊PI控制器的结构
1)模糊化
将采样得到的精确值转换成模糊量的过程称为模糊化[3]。例如将输入变量E和EC一般做如下划分:E={负大,负中,负小,零,正小,正中,正大};EC 同样。 对应于{NB,NM,NS,ZE,PS,PM,PB}。 系统速度误差 E和误差变化率 EC范围定义在模糊子集上论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。
2)隶属函数
MATLAB中提供5种隶属函数:三角形、梯形、钟形、高斯型和Sismoid型。一般系统模糊子集的隶属函数都是连续的,除去论域边界外,都是对称的凸F集[4]。一般实用中,远离系统平衡状态的平衡点,偏差较大时选用分辨率低的隶属函数;接近平衡点,偏差较小的范围选用高分辨率的隶属函数模糊集合。一般隶属函数越陡峭分辨率就越高,使其控制灵敏度增高,但是输出也越不平滑[5]。
本文正对输入输出的不同要求,选择不同的隶属函数。输入要求映射结果平滑,细化模糊推理,故选用高斯型隶属函数。输出要求响应快、分辨率高,故选用三角形隶属函数;并且在零附近,选用斜率大的三角函数以提高分辨率。如图2是输入E、EC和输出ΔKp、ΔKi的隶属函数图形。
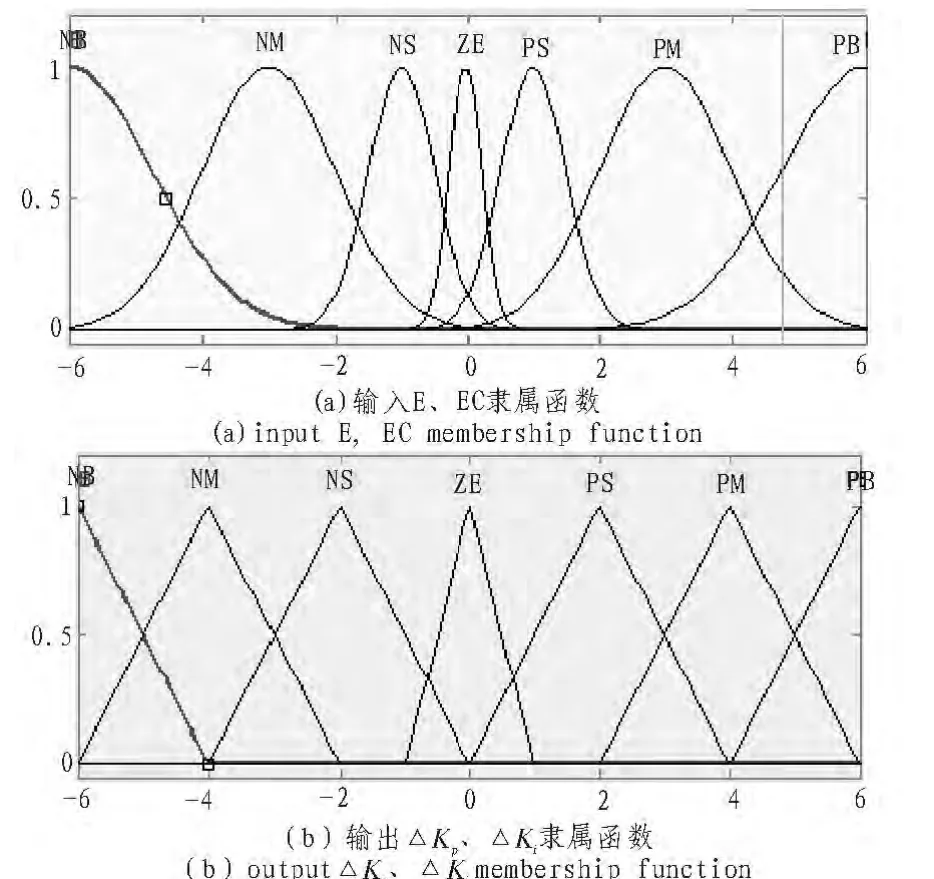
图2 输入输出隶属函数Fig.2 Input and output membership functions
3)控制规则
在MATLAB中,规则库是用于存放全部模糊控制规则,一般基于专家或手动操作人员长期积累的经验,按照人的直觉推理语言表示的形式。而模糊规一般是由一些关键词连接而成[6]。例如对本文中的输入变量为速度误差和误差变化率,对应语言变量为E和EC,则其一组模糊规则是:
R1:if E is NB and ECis NB,then Kp is PB ;
R2:if E is NB and ECis NB,then Ki is NB;
据此,本文对ΔKp、ΔKi参数分别建立对应的模糊规则表,如表1和表2所示。
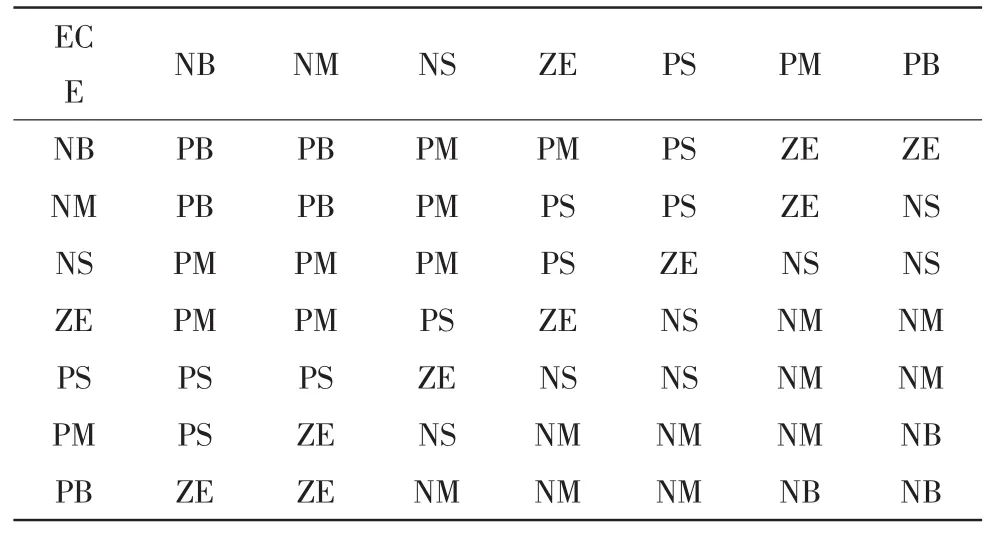
表1 2Δkp模糊规则表Tab.2 Fuzzy rule table ofΔkp
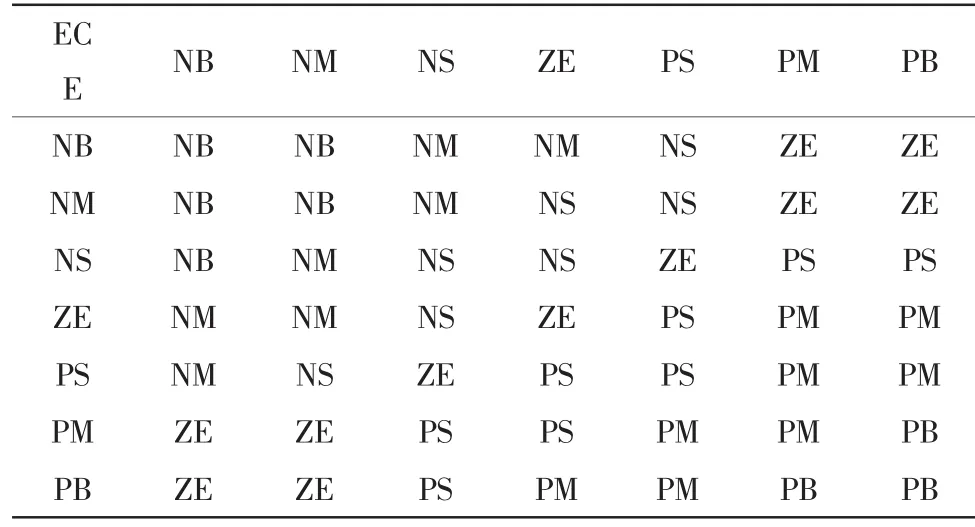
表2 Δki模糊规则表Tab.2 Fuzzy rule table ofΔki
4)量化因子和比例因子的确定
量化因子为清晰值从物理论域X变换到模糊论域N上的变换系数;比例因子为模糊论域到物理论域的变换系数。其作用都是信号的取值范围放大或者缩小,以适应设定的模糊论域的要求[7]。在控制器中,量化因子Ke、Kec和比例因子Ku是对系统动态性能有较大影响。一般,Ke越大,系统的超调就会越大,过渡过程也就越长;Ke越小,系统变化越慢,精度和稳态都会降低。而比例因子Ku,在系统响应的上升阶段,Ku越大,速度上升越快,但易引起超调,Ku越小,系统响应速度慢;在稳定阶段,Ku过大则会引起系统震荡[8]。Ke、Kec、Ku由下列各式确定:
Ke=量化论域值/基本论域范围;Kec=基本论域值/基本论域范围;Ku=量化论域范围/量化论域值。
本文SRD系统中,当速度的给定值ω*=1 000 r/min,系统的性能指标定为:误差e的变化范围不大于给定值的3%,误差变化率ec的变化范围不大于误差的5%。那么,误差e的基本论域为[-30,30],其量化因子 Ke=6/30=0.2,误差变化率ec的基本论域为[-1.5,1.5],其量化因子Kec=6/1.5=4。设参数ΔKp、ΔKi的调整范围为不大于已整定参数的18%,系统已整定参数为 Kp=10,Ki=60, 那么 ΔKp为:[-1.8,1.8]Kup=1.8/6=0.3,ΔKi的基本论域为[-1.8,1.8],其比例因子 Kui=1.8/6=0.3。
5)清晰化
模糊推理得到的控制变量是一个模糊量,不能直接控制被控制对象,需要将其转换为精确量。本文采用Mamdani推理方法,即加权平均法:将控制作用域上的点μi对模糊集合的隶属度μ(μi)加权系数进行加权,然后平均求得清晰值[5]。计算公式为:
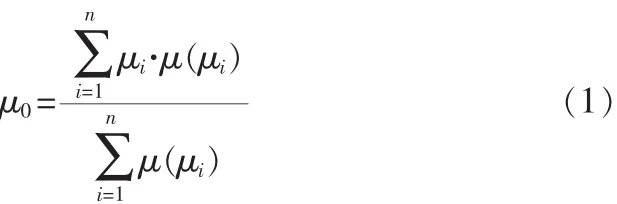
式中:μi为模糊量输出值,μ0为清晰化输出值,μ(μi)为模糊量的隶属度。
经过模糊逻辑调整得到修正参数ΔKp、ΔKi和PI控制器的初始值、分别相加后再输入PI控制器:

2 MATLAB/Simulink仿真及结果分析
2.1 MATLAB/Simulink仿真
经过模糊理论分析,在MATLAB/Simulink下搭建模糊PI控制器和开关磁阻电机调速系统并仿真。如图3和4所示。
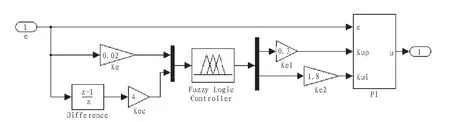
图3 模糊PI控制器仿真模型Fig.3 Fuzzy PI controller simulation models

图4 基于模糊PI的开关磁阻电机调速系统仿真模型Fig.4 Switched reluctance motor drive system simulation model based on fuzzy PI
本文SRD系统采用双闭环控制,即速度外环和电流内环。给定转速与输出实际转速差值经过模糊PI或常规PI,输出电流参考值,构成速度外环。输出实际电流经过位置检测输出与电流参考值比较构成电流内环。
仿真模型中具体参数设置如下:
1)仿真时间设为0.5 s;电机空载,初始给定速度为500 r/min;t=0.3 s时,速度突变为 1 000 r/min。
2)PI控制参数初始值为:Kp=10,Ki=60;模糊 PI控制器的量化因子和比例因子分别为:Ke=0.02,Kec=4,Kup=0.3,Kui=1.8。
3)开关磁阻电机(SRM)参数设定为:类型为四相8/6极,初始速度和位置为[0,0];额定电压为240 V;额定功率为10 kW。
4)位置检测模块的开通角为26,关断角52,开关磁阻电机采用双相启动方式启动,可使转矩波动小,平均转矩增大。
5)当初始给定速度为1 000 r/min,电机空载启动,当t=0.3 s时,给定转矩由0突变为20 N·m。
2.2 仿真结果及分析
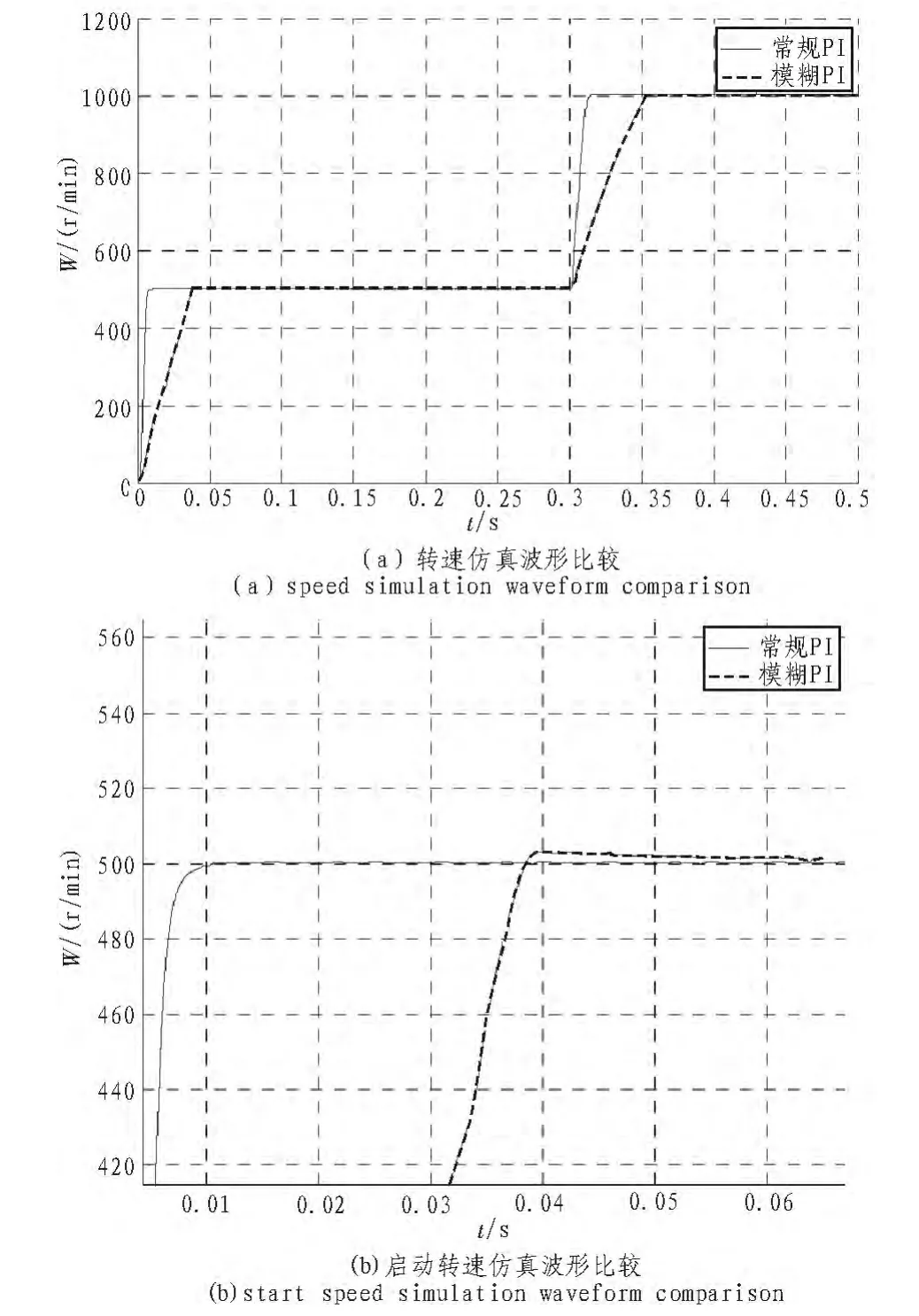
图5 模糊PI和常规PI转速仿真波形比较Fig.5 Fuzzy PIand PI speed comparison of conventional simulation waveforms
如图5所示:由图(a)可以看出,电机空载启动时,常规PI控制转速在t=0.04 s才到达500 r/min;而模糊PI转速时达到500 r/min;t=0.3 s时,电机转速突变为 1 000 r/min,常规 PI约经过t=0.06 s达到稳定转速,模糊PI控制经过t=0.01 5 s达到。由图(b)可看出,常规PI超调量约为1.2%,而模糊PI几乎为0。响应速度提高了40%,超调量减小1.2%,系统震荡也明显减小。综合可以看出,模糊PI控制[9]明显比常规PI响应速度快,且零超调,说明了模糊PI调节器根据模糊规则对PI参数在线实时调整,有效的提高了系统的静态和动态性能。
如图 6 所示,由图(a)和(b)可看出,t=0.3 s时,给定转矩由0突变为20 N·m,两种方式控制下的转速均有小幅震荡;负载时,常规PI控制的转速波动较大,而模糊自整定PI控制转速变化相对较小。由图(c)可看出,在稳定转速时,常规PI的静态误差月0.1%,模糊PI则为0;负载转速误差均约为0.1%。

图6 模糊PI和常规PI转矩突变转速波形比较Fig.6 Fuzzy PI mutations and conventional PI speed torque waveform comparison
3 结束语
综合上述仿真结果表明,将模糊控制和PI算法相结合控制开关磁阻电机调速系统的速度外环,利用模糊推理对PI的参数进行实时的在线调整,SRD的响应速度提高了40%,超调量减少了1.2%,大大提高了系统的调节精度及稳定性,减小了系统的超调和震荡。有效地改善了SRM非线性问题及开关磁阻电机调速系统(SRD)系统的静、动态性能。该方法对开关磁阻电机的调速达到了较为理想的控制效果。
[1]石辛民,郝整清.模糊控制及其MATLAB仿真[M].北京:清华大学出版社,2010.
[2]张志涌.精通MATLABR2011a[M].北京:北京航空航天大学出版社,2011.
[3]刘金琨.先进PID控制MATLAB仿真[M].3版.北京:电子工业出版社,2013.
[4]苏义鑫,王雁.基于模糊PID的开关磁阻电机调速系统研究[J].武汉理工大学学报,2010,2(5):21-26.SU Yi-xin,WANG Yan.Switched reluctance motor speed control system based on fuzzy PID[J].Wuhan University of Technology,2010,2(5):21-26.
[5]丛望,米芳芳.基于模糊PID的开关磁阻电机调速系统的建模与仿真[J].船电技术,2008,1(3):14-17.CONG Wang,MI Fang-fang.Modeling and simulation of fuzzy PID of switched reluctance motor drive system based on simulation[J].Boat Electric Technology,2008,1(3):14-17.
[6]王利博,游林儒,岳喜顺.基于自适应模糊PID开关磁阻电机调速系统仿真[J].电测与仪表,2012,3(4):21-25.WANG Li-bo,YOU Lin-ru,YUE Xi-shun.Adaptive fuzzy PID switched reluctance drive system simulation[J].Electrical Measurement&Instrumentation,2012,3(4):21-25.
[7]KHANAA,RAPALN.Fuzzy-PID controller:design,tuning and comparison with conventional PID controller[C]//Proc of the 2006 IEEE International Conference on Engineering of Intelligent System.China:IEEE Computer Press,2006,5(4):18-22.
[8]Cheok A D,Fukuda Y.A New torque and flux control method for switched reluctance motor drives[J].IEEE Transactions on Power Electronics,2006,5(4):18-22.
[9]谢永流,程志江,刘杰,等.带LCL滤波的并网逆变器改进PR控制策略[J].陕西电力,2014(6):21-24,68.XIE Yong-liu,CHENG Zhi-jiang,LIU Jie,et al.Improved PR control strategy for grid-connected inverter with LCL filter[J].Shaanxi Electric Power,2014(6):21-24,68.

